Journal of Advances in Physical Chemistry
Vol.05 No.02(2016), Article ID:17710,17
pages
10.12677/JAPC.2016.52007
A Quantum Chemistry Study of Hydrogen Bonds (2)
Guangyao Zhou
Beijing Kein Research Center for Natural Sciences, Beijing

Received: May 6th, 2016; accepted: May 27th, 2016; published: May 30th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Via quantum chemistry methods such as MP4(SDQ) and 6-311++G** basis-set, we conducted calculations on selected representative molecules that involved in various kinds of hydrogen bonds (H-bonds), and examined molecular orbitals as well as electron density difference (Δρ) before and after formation of H-bonds. We investigated formation mechanism of blue-shifted H-bonds by means of a new concept about H-bonds, proposed multiple forms of implicit interactions in molecules, and discussed inheritance, inclusion and development of the new concept about H-bonds with respect to past H-bonds studies.
Keywords:Quantum Chemistry, Hydrogen Bond, A New Concept about H-Bond, Blue-Shifted Hydrogen Bond

氢键的量子化学研究(二)
周光耀
北京科音自然科学研究中心,北京

收稿日期:2016年5月6日;录用日期:2016年5月27日;发布日期:2016年5月30日

摘 要
本文通过MP4(SDQ)等量子化学方法和6-311++G**基组,对各种类型氢键选择有代表性分子进行了计算,观察了形成氢键前后的MO和Δρ。用氢键新概念研究了蓝移氢键的形成机理。提出了分子中隐性相互作用的多种形式。讨论了氢键新概念对以往氢键研究的继承、包容和发展。
关键词 :量子化学,氢键,氢键新概念,蓝移氢键

1. 分子内、外孤对电子n构成的蓝移氢键机制
本文是上文《氢键的量子化学研究(一)》 [1] 的继续。
本文提出了氢键的新概念,显然还需要更深入细致地探讨。但这些探讨最关键的莫过于对产生蓝移氢键机理的解释,这是对氢键新概念的首要考验和演绎。
蓝移氢键自发现以来,引起了实验、理论的广泛注意和研究,见文献 [2] - [4] 的介绍。
所谓蓝移氢键,从氢键新概念看,是说在人所共知的氢键通式X-H⋯Y,Y的孤对电子n(或者单电子、π电子等)向X-H的反键空域转移了部分电子,本来应该使得X-H键拉长,却发现事实上在某些结构场合,这个X-H键、甚至和X相连的另外的键竟然发生键长缩短,即键的伸缩振动频率发生了蓝移。
对具体化学体系进行量子化学计算探讨蓝移氢键,自然会用多种方法、基组,比如MP2、MP4(SDQ)、CCSD等,对计算结果进行相互比对,以方法能否更好地描述出现氢键的红移(键伸长)和蓝移(键缩短)与实测的数据相符较好为标准 [5] 。在探讨蓝移氢键时,本文这部分主要采用post-HF方法之一MP4(SDQ)/6-311++G**。此外的方法则在文中说明。长度不标出单位时是Å。
对于氢键计算,MP4优化分子结构键长和能量之后,可以有两种数据输出:一种输出是基于MP4 density的,这是post-HF方法的,此数据本文用于全电子密度差Δρ。Δρ图示紫色为正值是电子密度增加区域、青蓝色为负值是电子密度减少区域。但是,post-HF方法的价轨道为分数占据轨道,不便采用单个的MO。另一种输出是基于SCF density的,它实际上是HF方法的,此数据本文用于分子轨道MO,其图示铁红为正值、苹果绿为负值。这涉及到“氢键MO”的形象、能级数据、相关MO上的电子密度差Δρ等。实践经验表明,HF方法与post-HF方法对于氢键的计算结果在定性上以及基本定量上是一致的,后面还会进一步说明这个问题,所以本文在研究氢键性质时这两种方法的数据有时是并用的,比如两种方法算的全电子Δρ图像在性质上是基本一致的。
蓝移氢键体系本身有各种具体的数据参数,不能拿其中一种参数直接来解释氢键引起的蓝移,比如不能用计算键长缩短来解释蓝移,而是要回答键长为什么会缩短?要回答蓝移时这些参数为什么会有这样的变化?
1.1. CH2O的氢键衍生物和蓝移氢键
为了叙述方便,现在把p型轨道两瓣延伸的方向称为纵向,把与之垂直的方向称为横向。
在众多的蓝移氢键研究中,顺–反(cis-trans)甲酸二聚体同时具有氢键的红移和蓝移是一个很典型的例子,值得首先拿出来深究。文献 [4] 用各种方法、从各方面探讨了这个二聚体,本文则是从氢键新概念出发来进行新的探讨。
讨论cis-trans甲酸二聚体(以下简称二聚体)的氢键的红移和蓝移的根源,不妨先选一个模型化合物来计算一下,把问题简化,然后再讨论二聚体。这模型就是甲醛CH2O,甲酸正是它的一边的H换成OH而已,另一边的基本格局还保留着,基本性质还保留着。
本文的前部分 [1] ,曾经算过CH2O,现在图1(a)是其分子内氢键MO8 (等值面取默认值0.02时不再

Figure 1. (a) MO8 in CH2O, (b) Δρ in CH2O⋯HOH, (c) Δρ in CH2O⋯(H2O)2
图1. (a) CH2O的MO8,(b) CH2O⋯HOH的Δρ,(c) CH2O⋯(H2O)2的Δρ
标出)。这是O的孤对电子n向CH2的p型势阱偏移电子降低能量形成的。CH2的p型势阱是两个C-H键电子反相位构成的,构成了一个反相位的p型势阱空间,在较低的空MO可以见到它的形象(LUMO + 1)。这里的“势阱”概念,是说真正没有电子占据时的LUMO + n (n = 0,1,2…),是一个已经形成价键的众核之间的一个低能的势场。由于n的p型电子横向偏移进入CH2的外围p型反相位空域,可称之为超共轭。n电子的母体与偏移电子、CH2的外围p型空域本身,都是反相位互相对峙的,呈现一种特征性地“蝶形排斥”。相对于一般C的sp2杂化与H成键键长数量级1.08,这种排斥使得C-H在CH2O中被撑长至1.10674 (3021.04——该键长下的伸缩振动频率计算值,单位是cm−1,下同)。
这时可以用“盆积分” [6] 的方法,求得O的n电子余额为1.2782,偏移到CH2上的电子为0.7216。但从图1(a)看,二CH处图形还大一些,这只表明它在反键空域电子密度低一些、蓬松一些。
在CH2O中的CH,本是C的sp2杂化与二个H的s成键。可以用一个具有两个单电子的CH2的来算一下CH在通常情况下键长的数量级。CH2的3个sp2杂化电子,两个与H成键,还有一个可以与O成σ键,剩下另一个单电子垂直分子平面,可以与O成π键。这样具有两个单电子的CH2中CH键长算得为1.08181。这个值可以作为sp2杂化CH键长的基本参考数量级。
在CH2O中CH竟被撑长了0.02493,这个分子内氢键由于分子骨架的限制是非常憋屈、有很大张力的。如果从传统的氢键CH⋯O看,它不仅是弯曲的而且是折叠的。
这时可以考虑分别从CH2O的两端作用于它,考察是否可以缓解、改变这种憋屈的张力。
于是可以拿一个H2O放在CH2O中O的孤对电子n处,进行优化计算,这样就形成了分子间氢键,见图1(b)所示的Δρ图。本来可以看到体系的分子内、分子间并存氢键的一个MO的,这里作成了Δρ图,因为Δρ图可以看见电子在体系中的变化情况。Δρ是由CH2O⋯HOH的MO13的ρ减去CH2O的MO8的ρ作出的。MO8是CH2O中O的孤对电子n偏移形成电子分布状况,MO13则是CH2O⋯HOH中这个羰基O的电子n又形成了分子间氢键的电子分布状况。这个Δρ图可以表明CH2O加H2O前后电子变化的具体情况。即使是作二者全电子的Δρ图,这种大趋势也是可见的,只是还有一些此外小的电子变化夹在其中使图稍微复杂一些。
图1(b)中,可以清晰地看到,CH2O中O的孤对电子n又与HOH形成了分子间氢键,它的n的p型电子是纵向偏移到了HOH的对称性相同O上的,同时CH2处的电子从H的端头回流C-H键处。导致了一定程度地缓解原CH2O分子内氢键憋屈的张力,这时CH键长回复缩短至1.10404 (频率3062.23),比CH2O中缩短了0.0027 (频率提高 + 41.09),发生了分子间氢键引起的蓝移。
还可以设想将H2O放在CH2O的H处也形成氢键,但由于此时CH⋯O远弱于OH⋯O,优化的结果氢键自动转移到O上了,还是一个图1(b)的结构。
于是可以在图1(b)的基础上,将第二个H2O放在CH2O的H处来形成氢键,优化后二H2O之间也形成氢键,见图1(c)。这个图是post-HF全电子的Δρ图,二H2O是作为整体来算的,以便抵消二H2O之间形成氢键时电子密度改变,只看二H2O对CH2O的影响。图1(c)除了保有第一个H2O的影响外,第二个H2O形成氢键时本也是H2O的孤对电子n横向偏移向CH2的反键空域,但是这却排挤了原来CH2O中憋屈的那个n电子,这样二H2O一拉一推,体系憋屈的张力得到进一步缓解,对应的键长缩短至1.10144(频率3094.90),比原来CH2O中的键长缩短了0.0053(频率提高 + 73.86),发生了所谓蓝移氢键。
从图1(c)看,在CH2处存在着分子内氢键与分子间氢键竞争。而CH2处的势阱能级比H2O的n电子能级还是要低,H2O的n也要偏移电子过去,由于Pauli互斥,这多少排挤了分子内那个n电子,从而使得憋屈张力得到缓解、CH键缩短。这作用要大于分子间n电子偏移到反键空域引起的C-H键增长,分子间氢键毕竟有更大舒展余地可以减少斥力。这里,第二个H2O形成的分子间氢键时n电子是横向移动过去的,也是一种超共轭,与分子内氢键对称性允许。如果这个分子间氢键n电子是纵向移动过去的,那它与分子内氢键对称性却是正交的,之间没有直接作用。
1.2. cis-trans甲酸二聚体的蓝移氢键
cis-HCOOH的MO12见图2(a),它与CH2O的MO8基本一样,都是O的孤对电子n向CH2或CHOH的p型势阱偏移形成的,由于n电子偏移进入CH2或CHOH的外围p型为反相位空域,对于n电子的母体与偏移电子、CH2或CHOH的外围p型空域,都是反相位强烈排斥的,以至C-H在cis-HCOOH被撑长至1.10494(频率3021.65),sp2杂化C-H键长数量级为1.08181。这里也可见“蝶形排斥”的基本形象。
在cis-HCOOH中C-H被撑长了0.02313,这个分子内氢键由于分子骨架的限制是非常憋屈、有很大张力的。这时也可分别从cis-HCOOH的两端生成分子间氢键,考察是否可以缓解、改变这种憋屈和张力。
拿一个H2O放在cis-HCOOH中羰基O的孤对电子n处,进行优化计算,这样就形成了分子间氢键,见图2(b)所示的全电子Δρ图。
图2(b)中,可以清晰地看到,cis-HCOOH中O的孤对电子n又与HOH形成了分子间氢键,它的n电子的p型电子纵向偏移到了HOH的对称性相同O上,同时CHOH处的电子向羰基O处部分回归,C-H处的电子有所浓集。这些导致缓解了原cis-HCOOH分子内氢键的憋屈张力,C-H键长回复缩短至1.10209(频率3064.57),比cis-HCOOH中缩短了0.00285 (频率提高+42.92),发生了所谓蓝移氢键。
当然会想到把H2O放在cis-HCOOH的C-H处形成氢键来观察,但是这里形成CH⋯O远弱于OH⋯O,自动优化到羰基O处了。这不合考察从C-H处起作用的目的。
于是可以在图2(b)有一个H2O的基础上,将第二个H2O放在cis-HCOOH的C-H处来形成氢键,优化后二H2O之间也形成氢键,见图2(c)。这个图是全电子的Δρ图,二H2O是作为一个整体来算的,以便抵消二H2O形成氢键时的电子密度改变,只看二H2O对cis-HCOOH的影响。图2(c)除了保有第一个H2O的影响外,第二个H2O形成氢键时本也是H2O的孤对电子n横向偏移向CHOH的反键空域,但是这却排挤了原来cis-HCOOH中憋屈的那个n电子,这样二H2O一拉一推,体系得到进一步缓解,这时

Figure 2. (a) MO12 in cis-HCOOH, (b) Δρ in cis-HCOOH⋯HOH, (c) Δρ in cis-HCOOH⋯(H2O)2, (d) Δρ in cis-trans noncyclic formic acid dimer
图2. (a) 顺-HCOOH的MO12,(b) 顺-HCOOH⋯HOH的Δρ,(c) 顺-HCOOH⋯(H2O)2的Δρ,(d) 顺–反甲酸二聚体的Δρ
对应的键长缩短至1.10018 (频率3094.25),比原来cis-HCOOH中的键长缩短了0.00476 (频率提高 + 72.60),发生了所谓蓝移氢键。
构造cis-HCOOH与trans-HCOOH生成两个氢键的二聚体,优化结果见图2(d)所示的全电子Δρ图。这图与图2(c)何其相似,尤其是右边的cis-HCOOH,电子变化基本上是相同的。因为此时cis-HCOOH形成的两个氢键,与cis-HCOOH和二H2O效果是一致的。这样,上边的氢键从cis-HCOOH的羰基拉电子,而下边的氢键供电子,cis-HCOOH的分子内氢键体系得到进一步缓解,这时它的C-H键长缩短至1.09978 (频率3096.63),比原来cis-HCOOH中的键长缩短了0.00516 (频率提高74.98),发生了蓝移氢键。
现在看图2(d)上边的氢键O-H⋯O,这里的O-H不在trans-HCOOH的超共轭整体架构之内,参照超共轭图2(a),就没有O-H出现,这时O上的值是C-O键的,O-H的MO与体系超共轭是正交的。
这里,自由单体trans-HCOOH的O-H键长为0.96592 (频率3834.15),为通常的O-H键长数量级。而在二聚体中,右边cis-HCOOH羰基O上的n电子纵向偏移到左边trans-HCOOH的O-H反键空域,即O-H是O的p与H的s的反相位对峙,拉长了O-H,使得O-H伸长至0.97795 (频率3594.93)。发生了所谓红移氢键。
1.3. FPH2⋯FH的蓝移氢键
文献 [7] 研究了FPH2等质子给体与HF等质子受体形成的分子间双接触弯曲蓝移氢键,对氢键蓝移的机理进行了理论研究,本文以其典型的例子FPH2⋯FH,从氢键新概念出发来进行新的探讨。
从电子结构看,FPH2还真是与OCH2相类似。图3(a)中是FPH2的氢键MO12,它也呈现一种特征性“蝶形排斥”。这是F的孤对电子n向PH2的p型势阱偏移形成的,也是一个分子内超共轭、氢键。
由于n电子横向偏移进入PH2的外围p型为反相位空域,n电子的母体与偏移电子、PH2的外围p型势阱空域,都是反相位排斥的,以至于P-H在FPH2中被撑长至1.36962(频率2786.44)。
这时可以用“盆积分”的方法,求得F的n电子余额为0.4404,偏移到PH2上的电子为1.5386。这是由于F的电负性远远大于P,在σ键有过多的电子转移到F上,F的孤对电子n的能级被大大抬高。在自由的F原子,它的n电子能级为−0.73365,而在FPH2中,它的一个n电子能级因为电子向PH2偏移而降低,另一个n电子能级这时为−0.30506(也因有另一个n电子偏移走电子有所下降),可以作为F上n电子被抬高的数量级参照。另一方面,PH2因在成键时失去了大量的电子,能级下降得很低,其外围产生很低的势阱。这就构成了F上大量的n电子偏移到PH2,才能达到能级均衡、电负性均衡。
构造氢键分子FPH2⋯FH,来观察形成分子间双接触弯曲氢键时对FPH2的影响。图3(b)是该氢键分子全电子的Δρ图像,从整体看,FH的n电子横向偏移到PH2的外围p型为反相位空域,偏移的电子量为 0.04452,由于形成的分子间氢键使得FPH2的电子朝其上F的方向返还了电子,这意味着缓解了原来的分子内超共轭氢键的张力,P-H键长缩短至1.36793 (频率2804.86),缩短了0.00169 (频率提高 + 18.42),发生了所谓蓝移氢键。这里,仅从分子的末端形成的分子间氢键排挤分子内超共轭的n电子,导致P-H
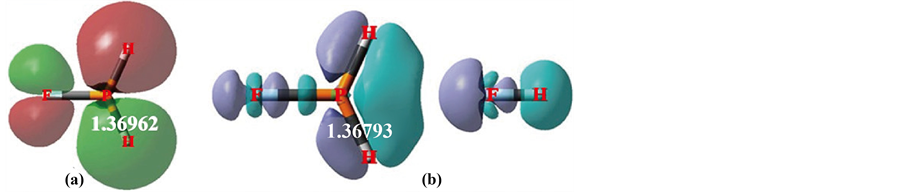
Figure 3. (a) MO12 in FPH2, (b) Δρ in FPH2⋯FH
图3. (a) FPH2的MO12,(b) FPH2⋯FH的Δρ
键长缩短。
1.4. F3CH⋯NH3的蓝移氢键
对于上述孤对电子n的超共轭构成的蓝移氢键机制,可以记为n→π*。这是一种p型轨道的横向移动。
然而,电子n在分子中不仅能形成超共轭,还会在对称性允许、不正交的情况下,向近程的σ*反键轨道偏移电子以降低能量,构成的蓝移氢键的另一种机制,这可以记为n→σ*。这是一种p型轨道的纵向移动,故也可以记为p→σ*。下面F3CH⋯NH3就是这样的例子。
图4(a)是F3CH的HOMO,为了使图明晰,等值面取为0.08,两个完全一样的F重叠在一起了。3个F的部分n电子向C-H的反键轨道纵向偏移了电子,它是要拉开C-H的,n电子具体落在反键轨道分离出来的C的p型轨道上。
这时C-H键长为1.08944 (频率3113.89)。我们不能得知C连上3个F时纯粹的C-H键长是多少,经验推测它应该比这个值短得多,现在是F的n电子有少量出现在C-H的σ*上把它撑长了。
可以设想在C-H处生成分子间的氢键来影响C-H键长,观察蓝移的机理。可用NH3的孤对电子n来构成分子间氢键F3CH⋯NH3。F3CH⋯NH3的HOMO其实就是分子间这个氢键MO的形象,见图4(b)。
在自由NH3中,由于电子向N转移,N上电子排斥加大,其上的孤对电子n能级被抬高,HF方法计算能级为−0.42437。而F3CH的HOMO (图4(a))能级是−0.59694,它的C-H反键轨道在没有电子占据时可以参照这个值,而不是占据了一个电子时的LUMO值 [1] 。由于3F拉走许多电子C-H处形成了一个低能势阱,在其σ*又接受了F的部分电子后,它的能级还低于NH3的孤对电子的能级,还能与NH3的孤对电子形成分子间氢键。
图4(b)是F3CH⋯NH3氢键的MO,且是HOMO,它表明,NH3的孤对电子n向C-H反键轨道排布了电子,而且波及到了3个F。因此可以作F3CH⋯NH3的这个氢键MO与NH3的孤对电子n的MO作电子密度差,见图4(c)。
图4(c)总的说来,NH3的孤对电子n减少了,部分纵向转移到C-H的反键轨道之上了,C-H的反键空域是C的p型轨道与H的s型轨道反相位对峙,NH3的电子n为p型轨道与H的s正交,电子转移到C的p型轨道上了。同时使得C上3F相应的p型轨道有所增值。这时C-H键长缩短至1.08840 (频率3213.49),键长缩短了0.00104 (频率提高99.6),发生了蓝移。
在这个例子中,F3CH具有产生氢键引起蓝移的潜质、机制,是内因。在形成分子间氢键时,对外因Y的p型电子的能级高低还是有要求的,如果用·CH3来形成氢键,就不足以发生蓝移氢键。
就氢键通式X-H⋯Y而论,如何解释在C上F的电荷增值?
Hobza [3] 认为是:Y没有向X转移电荷,而是向比X更远处的电负性原子转移了电荷,从而使分子发生结构重排,最终致使X-H键长缩短,X-H伸缩振动频率蓝移。
本文则理解为:NH3的孤对电子n向C的反键轨道空域转移了电子,从而挤走了部分原先占据在这

Figure 4. (a) HOMO in F3CH, (b) HOMO in F3CH⋯NH3, (c) Δρ in F3CH⋯NH3
图4. (a) F3CH 的HOMO,(b) F3CH⋯NH3的HOMO,(c) F3CH⋯NH3的Δρ
里的3F的n电子,使之部分回归。这种电荷回归,释放了对C-H键的斥力。本来NH3的电子n向C-H的反键轨道转移电子也是要拉开C-H键的,但是这个分子间氢键造成的排斥在中程,它所形成的斥力比分子中C上3F的近程斥力要小,C上F的电荷回归对C-H键的斥力减小占了上风,从而使得C-H键长缩短,C-H伸缩振动频率蓝移。
本来,电子是不可识别的,C上3F的电荷增值到底是回归还是NH3的n电子,是不能判明的。但是考虑到3F是n电子,NH3也是n电子,它们是有Pauli排斥的,说是NH3的n电子挤走3F的n电子,比说成NH3的n电子转移到3F的n电子处要合适。
这就是n→σ*或p→σ*蓝移氢键的机制。NH3的n电子是高位的水流向低位C处,C处水位升高水又回流至3F,直至N、C和3F的水位均衡,参与构成氢键的原子轨道(基组线性组合)能级均衡、电负性均衡,构成统一的MO。
n→π*被称为超共轭,那么n→σ*不妨称为“超σ”。因为n电子部分转移到σ*空域上形成电子共享是σ性质的,但它不同于分子内的σ键、也不同于配位键。这后二者都是成键双方共享电子,共享电子没有截面,而氢键偏移电子与母体是反相位的,二者之间有截面,这里的电子是处在反键轨道上。当然,说存在反相位相斥是仅对电子而言的、是电子布居内部的,它们在核之间又整体处于共享电子地位。
1.5. n电子形成的蓝移氢键是蓝移氢键的主要机制
在探讨蓝移氢键的机制时,必定会收集蓝移氢键的各种类型来进行观察分析。早在2000年Hobza [2] 就将已发现的蓝移型氢键体系总结为4类:
CH⋯π共轭体系型;CH⋯O型;CH⋯F型;CH⋯X− (卤负离子)型。
这是在氢键通式X-H⋯Y中以Y来分类的。在通常氢键体系这个通式是合用的,但在蓝移氢键情况下这个通式就不那么可用了。
从本文上面已经讨论的例子看,虽然分子间形成蓝移氢键时Y是个重要的环节,但Y显然不是氢键发生蓝移的核心机制部位。根据上面的例子,可以把蓝移氢键格局的通式写为Z≈X-H⋯Y。这个式子的基本思路和格式在文献 [2] [3] [8] 曾经有过,本文则进一步探讨它的具体的机制细节。这里,≈代表Z与X的多键或者多重键的连接,Z≈X才能包含蓝移氢键机制的本源,它是内因,Y是外因,外因通过内因起作用产生蓝移氢键,Z≈X才应是对蓝移氢键分类的依据。
探索蓝移氢键的机制,从对比形成蓝移氢键的前后变化入手无疑是必由之路。于是学者们发现了重极化与重杂化和分子内超共扼在氢键的蓝移时也相应发生了变化 [8] ,此时相关的键缩短了,它的红外谱线发生了蓝移。然而这些反映氢键蓝移的特征参数,并不能直接揭示蓝移的机制,比如不能解释说因为相关的键缩短了所以蓝移。问题在于相关的键为什么会缩短?为什么会重极化与重杂化?为什么分子内超共扼会这样变化?
对于分子内n电子所形成的蓝移氢键机制,又可分为n→π*和n→σ*。
对于n→π*,分子内超共轭是关键。这个所谓超共轭,是Z≈X-H中,比如甲醛OCH2,Z(O、N、F、Cl等)的电负性远大于X (C、N、S、P等),Z在σ (或者还有π)从X-H拉走了较多电子,使Z上的电子量增加,电子排斥增大,其上的孤对电子n的能级被抬升得很高。它的对立面X-H呢,因失去电子而能级下降,在其周围形成低能势阱,这势阱即是该键外围的反键空轨道。当Z上的n电子与这个势阱对称性允许、不正交时,n电子会向这个势阱横向转移部分电子,以达到能量降低并均衡、电负性均衡。由于n电子近距离横向转移到反键空域,这里不像分子间氢键那样有足够的回旋余地、可以拉开距离,所以斥力使得相关的键伸长了许多,这使得外面再有另外的n电子也因为能级差来挤占这个X-H处势阱时,原来的n电子会退缩,斥力减退,使得相关的键缩短,形成蓝移。相比之下,外来的n电子因有足够的回旋余地对相关键的斥力作用来得较小。这时分子内、分子间都必须是形成超共轭才能起作用,如果Y提供只是σ性质的电子,那么它与分子内的超共轭是正交的,将不起作用,不能产生蓝移氢键。除非是从Z处形成氢键导走了电子。
对于n→σ*,没有分子内超共轭的机制。这时,Z因电负性高而得到电子,其上的孤对电子n的能级被抬升得很高,X-H却失去电子形成低能势阱,Z的p型n电子会纵向进入X-H的σ*轨道以降低能量。当形成分子间氢键,Y的p型n电子也是纵向进入X-H的σ* 轨道,挤占原来已占据的Z的n电子使之回退,从而产生蓝移氢键。同样,这时分子内、分子间都必须是σ性质的电子才能起作用,否则是正交的,将不起作用,不能产生蓝移氢键。
当然,Z的n电子也可以另成分子间氢键,产生Z的n电子从X处回退,使X-H键长缩短、蓝移。
在更广泛的蓝移氢键体系,还有另一种类型,它没有n电子,且称之为v型,这在下面才专门讲到。
这里以Z≈X-H为通式归纳一些具备产生蓝移氢键机构的例子,基于这些基元结构的更多衍生物没有列出。
n型蓝移氢键例(具有n电子、单电子、π电子的Y没有列出):
OCH2、OCHOH、OCHNH2、ONH、OCHCl、FPH2、F2CH2、F3CH、Cl3CH、HOPH2、FCH3、ClCH3、BrCH3、ICH3、F2NH、F2PH、FNH2、F3SiH、SNH、FOH、HNCHCHCHOH
v型蓝移氢键例:
垂直型二苯二聚体(C6H6)2。
2. 分子内、外键电子之间排斥构成另一种蓝移氢键机制
2.1. 引起蓝移氢键的分子内隐性相互作用
当涉及到分子间的相互作用,如范德华作用、氢键时,我们不妨说范德华作用是长程的,长度数量级约在3左右或者更长;说氢键是中程的,长度数量级约在2左右或者更长(以H⋯Y衡量);还可以说n电子分子内超共扼是近程的,一个原子上相邻两个键是近程的,长度数量级约在1.5左右或者更长;分子内的键长是短程在1左右或者更长。
说到这里,不禁会产生一个疑问:比如说范德华作用,为什么只在长程才有作用?为什么一种作用在长程时已经显现出来,而中、近程反而不见了?这似乎不合逻辑!
平常对于一个分子体系,常用单双键将原子连起来代表价键,用虚线画出氢键、范德华作用,在价键的基础上还有诱导作用、共轭作用等,这些之外的作用常常被忽略不能被标识出来,视而不见,现在本文称呼它们为隐性相互作用。因为现在正是这些隐性相互作用,决定了氢键引起的蓝移机理,当然这里只讨论导致的氢键相关键频率蓝移的隐性相互作用。上面形成蓝移氢键机制的n电子就是分子内隐性相互作用之一。下面是另一种引起蓝移氢键的分子内隐性相互作用,即范德华作用。
2.2. 范德华作用的新概念
我在以前的系列文章 [9] ,提出了范德华作用的新概念,范德华作用的主要机理、特征可以归纳为:
范德华作用的本质是分子(含原子)的配对电子(如价键)之间的作用。
当双方都已是价键完善的配对电子的分子(含稀有气体原子)相遇、相碰时:
如果双方形成电子云球是完全刚性的,会即碰即离。这是物理力学的。
如果这电子云球是半刚性的,电子云球会发生变形,双方配对电子相互之间会退让,分子之间相对的空域电子会被挤走,此处的核较裸露,它会使核之间的排斥增强,斥力增大,从而还是分开。
然而相遇、相碰的电子云球完全是塑性的,电子是灵动地按各处电负性大小作概率出现、分布的。当较裸露的核排斥、电子排斥使双方拉开到一定距离(范德华距离)时,排斥迅速减小,双方比较裸露的核处吸引电子的能力增强却凸显出来了,裸露的核是不排斥电子的,反而会在双方较裸露的核之间重新增加电子聚集,形成了分子间电子共享的增加。共享电子又主要布居在二核之间,直接减小了核与核之间的排斥,从而抗衡了双方的配对电子的排斥和核排斥,达到平衡,形成了范德华作用。这是化学的。
我们曾对这种分子之间的范德华作用做过扫描(scan),还做过扫描全程的Δρ动画。当双方距离在近程、中程时,较裸露的核排斥、电子排斥使双方核之间电子聚集急剧减少,双方之间的斥力倍增,双方被拉开。当距离拉开到范德华距离时,相互作用的量变引起质变:双方较裸露的核之间电子聚集却重新增加,共享电子的重新增加形成了引力,平衡了双方核和电子的斥力,产生范德华作用。如果再拉开距离,双方核和电子的斥力逐渐减小直至无,核之间电子聚集也恢复常态,双方各自成为自由体了。
这就是两边都是电子配对MO,在对称性允许、不正交时,范德华作用的全过程。虽然历史上学者们是从维系了体系的弱稳定性认识范德华作用的,但如今我们不妨把这全过程都看成范德华作用。只是这作用在近程、中程都为排斥力占上风而已,可以称为范德华作用的排斥阶段。
如果仅从MO来看这个全过程,发生范德华作用的双方都是电子配对的MO,它们会形成两个轨道安排两对电子:一个MO是同位相的,表达了双方基本的能级和潜在的引力,另一个MO是反相位的,表达双方毕竟是配对电子、存在Pauli互斥,是反键性质的。随着双方距离变化,斥力和引力此消彼长,但只看MO不易辨别,而作Δρ对变化则一目了然。
其实,无论分子内、分子间,电子配对的价键之间都是存在这种范德华作用的。
2.3. 氢键分子的中程范德华作用
在此文的前半部分,在对各种氢键体系进行MO分析时,都说到Y的孤对电子n(或者单电子、π电子)向X-H的反键空域转移了部分电子,构成超共轭(或超σ)体系,形成氢键MO。同时还有几对MO被说成是“氢键相关MO”。这是当超共轭(或超σ)形成氢键时,它同时拉拢、锚定了对称性允许不正交的几组双方MO,双方都是电子配对的MO,它们会分别形成两个轨道安排两对电子,一个MO是同相位的,表达双方潜在的引力,另一个MO是反相位的,表达双方的斥力。这些就是“氢键相关MO”。
由于氢键锚定了双方的距离为中程,这时所拉近的双方都是电子配对的MO,它们主要是微弱排斥的,属于范德华作用的排斥阶段。
因为算氢键结合时总是会包含这种微弱排斥的,故称之为“氢键相关MO”,可以认为它是包含在氢键中的范德华微弱排斥作用。
是不是还会有排斥超过中程,氢键还维系着,这氢键相关MO转化成范德华微弱吸引作用,也是有可能的。
氢键与范德华作用,因为氢键是单方的n电子部分转移到对方π*(或σ*)空域上,并不是双方都是配对键电子的MO相遇,机理完全不同,不能相互归属。
2.4. 分子内价键之间的近程范德华作用
上面看到氢键中的中程的范德华微弱排斥作用。
分子内那么多MO,多是在表达原子之间成键、反键或非键的,多是电子配对的MO,它们之间有各种对称性。当两个键相邻且不正交,处于近程,这时就会有一个MO描述它们是同相位的,表达双方能级和潜在的引力,用另一个反相位的MO,表达双方的斥力。这都可以看着是范德华作用的特征,它们之间的作用属于范德华作用的排斥阶段、或者吸引阶段。
之所以要讨论这个问题,是因为在众多的蓝移氢键例子中,虽然绝大多数的蓝移机理可以归纳入分子内n电子超共扼(或超σ),被称为n型蓝移氢键,但是还有一类并没有n电子,比如垂直型二苯之间形成的蓝移氢键,它的蓝移机理是由中程、近程不同键电子相互排斥形成的,这作用可以归纳为范德华作用的排斥阶段,故把此类标记为v型蓝移氢键。
氢键引起的蓝移是由键长缩短引起的,现在就从键长追究下去。
经验和实验表明,C-H键长,首先取决于C上独立的键电子与非键电子(孤对电子、单电子)在空间取向所构成的互斥和基本杂化,它决定了键长的基本数量级。如C-sp3杂化与H形成的键长为1.09,CH4键角为109.47;C-sp2杂化与H形成的键长为1.08,CH3键角为120.0。
然而,这些键长都是C上不同的键电子以及非键电子之间的近程排斥下形成的。例如C-H安排为一个C-H键和三个单电子,键长为1.07,它是C-s形成的键,可以作为单个C-H键长数量级的参考。又例如在CH2中,如果安排为两个C-H键和两个单电子,由于两个C-H键上的配对电子比两个单电子的排斥要大,计算没有得到四个基本等性sp3杂化,得到的是两个C-H键夹角大至132.6,键长达到1.08169,它比独立单个C-H键要长得多。
可以作CH2与两个独立C-H键的电子密度差,见图5(a)。它近似地表达了当两个配对电子的C-H键近程相处时,双方配对电子会产生Pauli排斥,电子因相互排斥移向H的外端,键被撑长,键角撑大。这可以看作是双方键的配对电子近程相处的范德华作用排斥的结果。
苯中的C-H键是由C的sp2杂化与H的s成键的,这样的键在没有受到近程其它键作用时它的键长数量级应该是多少呢?
我们是无法计算C的sp2杂化的纯粹单个C-H键以及它的键长的。但可从简单实例考察它的数量级。
在CH3中,C的sp2杂化与H的s成键,C-H键之间夹角为120度,键长1.08370。这里每个C-H键近程都有两个C-H的σ键相伴相斥,键长被撑长了。不受夹持的纯sp2杂化C-H键应短得多。
在CH2=CH2中,C的sp2杂化与H的s成键,C-H键之间夹角为116.1度,C-H与C=C之间夹角为121.6度。这里一个CH键被近程相连的一个C-H键和另一个C=C双键所夹持,斥力增加得更大了,键长被撑长至1.08644。这里C-H与C=C之间夹角为121.6度,可见有双键时排斥更大点。
在苯C6H6中,一个C-H键近程两边都有σ、π键相邻,因排斥键长被撑长至1.08650。
2.5. 垂直型二苯的蓝移氢键
垂直型二苯二聚体是早年由Hobza等人 [10] 论计算预测到蓝移氢键的,并认为这种蓝移氢键形成的原因是由于分子间的色散作用,所谓色散作用历来被认为是范德华作用,现在具体分析一下这个作用。
从单个自由苯的MO图像看,它的HOMO是处于对位的两个CC的π键,两个π键之间反相位,参见二聚体图5(b)左边的侧面苯。自由苯的LUMO是全部6个C-H的σ*反键轨道,是C的p型轨道与H
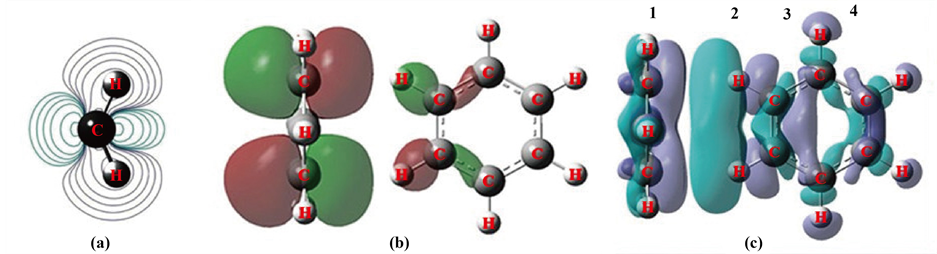
Figure 5. (a) Δρ in CH2, (b) MO40 in the Benzene Dimer, (c) Δρ in the Benzene Dimer
图5. (a) CH2的Δρ,(b) 苯二聚体的MO40,(c) 苯二聚体的Δρ
的s型轨道的反相位对峙。这时LUMO是空的,它表达了一种性质、一种能力、一种势阱。LUMO的能级计算值是设想有一个电子占据该轨道时的值,若无电子占据时它是C-H的σ键外围空间的低能势阱 [1] 。
垂直型二苯二聚体组合方式,文献 [10] 采用一个苯的一个C-H垂直指向另一苯的中心,我们除重复文献这个结构外,还计算了一个苯(图5(b)右边的正面苯)的两个C-H指向另一苯(图5(b)左边的侧面苯)的对位的两个π键的中部,二苯相互垂直,本文用此结果。
全优化后这里形成了两个分子间氢键,但用图形解释氢键所导致的蓝移机理却较明晰。图5(b)的MO40就是用来反映两个氢键的轨道的,等值面取值0.07。取此值隐去了氢键所引起的波澜,只突出氢键这个主体的形象。
此处形成的氢键轨道MO40,它是左边的侧面苯处于高能级的两个π键电子向右边的正面苯的低能势阱偏移部分电子形成的,偏移电子量从相应的MO作Δρ可以得到:左边的侧面苯失去电子,为-0.08560,右边的正面苯得到电子,为+0.08560,当然这是两个氢键偏移电子的总量。从MO40看,不仅一个氢键的两部分电子是反相位的,而且两个氢键之间也是处处以反相位对峙的。这里两组氢键又呈现出了“蝶形排斥”。虽然左边的侧面苯看似以π电子来构成氢键,但实际上却是组成π键的p型电子纵向偏移到对方C的p型空轨道构成氢键的。这时,这个π电子与n电子一样都是配对电子,同属于p→σ*。
以这种垂直方式构成的氢键二聚苯,左边的侧面苯以两个CC的π键作前锋将部分p电子纵向抛向对方势阱中以降低能量,平衡了拉近、锚定双方所产生的双方键电子之间的斥力。这斥力虽然不足以改变右边的正面苯的价键结构,但却使得价键上的电子发生了变形、偏移,这种情况被氢键二聚苯与二苯的全电子Δρ真实地记录下来了,见图5(c),等值面取值0.0002。
将图5(c)之Δρ分段来看,它一波又一波,主要共4波,用1~4标示在图中。
第1波,左负右正,这是始作俑者,是两个处于对位的CC的π键,π键的CC图中重叠在一起了。图形表明它们的电子向前面的势阱倾倒了,并且二个氢键向对面的势阱C处共偏移了0.08560电子,从而降低了能量,锚定了双方,形成了氢键。在C-H键σ*上的H虽然是空位势阱,但却与纵向偏移过来的p型电子正交,电子没有落在此处。
第3波,需要提前说它,这里是承接对方偏移过来电子的所在。右边苯CC的π键p型电子纵向偏移到对方苯C的p型(σ*)上,π键的p型轨道具有配对电子性质,它的纵向偏移对右边苯形成氢键的C-C的σ键形成冲击,这是范德华排斥,这个C-C的σ键电子发生了后退变形。同时,左边苯的π键p型电子虽然与右边苯形成氢键的两个C上的π键的p型电子是正交的,但是由于毕竟这两个C的σ*接受了电子,使其上的π键的p型电子能级被抬高也发生了电荷偏移。这样σ、π电子偏移共同形成了第3波,在电荷变化上也是顺应冲击左负右正。这种电子位移的第3波,缓解了对近程相连的两个C-H键电子的排斥,使C-H键长缩短了,单体苯中原为1.08650,氢键二聚苯中缩短至1.08059,这时便产生了蓝移氢键。
第2波,回头再看它,也是左负右正。这本是C-H键H的势力范围。原本C-H键近程两边有σ、π键相夹持,C-H键电子排斥向H的外端,现在由于对方CC的π键配对电子袭来,使σ、π键受排斥后退,对C-H键的夹持减弱,加上从H的外端有电子冲击过来,电子部分回到键中间了,加强了C-H键,使键缩短。
第4波,它是第3波电子移位的余波,电荷移位也是左负右正,也是σ、π电子共同形成这一波移位。只是与第3波比起来,这里的σ电子反而不及π电子的量了。从物理有机的诱导效应和共轭效应,可以理解为σ通过诱导传递,经过一个C, 诱导效应降低大约1/3,而通过大π键的共轭效应传递并不怎么衰减。
这里,分子内、外键电子之间范德华作用的排斥构成另一种蓝移氢键机制:
先是苯分子内键电子之间排斥使C-H键撑长了。当与另一分子形成分子间氢键时,另一分子延伸、偏移过来的具有配对电子性质的p型电子,对原来分子内的键电子之间排斥发生冲击,分子之间又被氢键锚定了距离,原来分子内的键电子上的电子云发生后退变形(实际上还包含:形成氢键的C上接收了电子,电子会沿着σ、π键传递转移),从而缓解了对C-H键电子的斥力,此处C-H键就缩短了,发生了蓝移。
3. 氢键新概念对以往氢键研究的继承、包容和发展
3.1. 关于氢键研究的发展
关于氢键的发现、定义以及理论研究的发展历程有大量的综述 [11] - [14] 。
氢键一直以来用一个通式来表达它:X-H…Y,认为是缺电子的质子H拉住了高电负性的X、Y,X-H是质子供体,Y是质子受体,故而称为氢键。这种高度的概括、定义,曾经大大地促进了对氢键的实验发现和理论研究的发展。
然而,随着对氢键的实验和理论研究的广泛、深入,H还可以换成Li、Na等,还有双氢键等等,特别是发现了蓝移氢键,开始认为是一种反常氢键(Anti-Hydrogen Bond),这些都给氢键是质子H的给、受的理论概括带来了冲击和思考。
在蓝移氢键中,理论计算发现随着蓝移氢键的产生,相关的原子在分子中会重杂化、重极化,分子内超共轭也发生了变化。还发现Y的电子竟转移到与X相连的别的原子上了,甚至通式之外的键也会同时出现蓝移。还发现多接触的弯曲氢键,如FPH2⋯FH,这里用电子密度拓扑分析 [7] ,H⋯F之间并没有作为氢键特征的键临界点,反而在P⋯F之间有键临界点。这些研究都突破了通式,需要进行新的概括、建立新的概念,概念需要扩大,以便包含这些新发现的事实。
其实,只要和盘托出理论计算所反映的客观事实即可形成氢键的新概括、新概念。在通式X-H…Y中,需要把历来以H作为氢键的中介、中心的视角转移到X处,这样更符合客观存在。说“X处”,既指X这个原子的σ*,也包含X处价键所形成的π*。
在氢键中,都是处于能级高位Y的p型电子部分转移到X处所构成的反键空域π*或者σ*从而降低了体系的能量。H不再是关注的中心,它可以在任何位置,它只是配合X构成反键空域π*或者σ*而已。在π*或者σ*中,H是s型空位势阱,与Y的p型电子正交,Y的p型电子不会落于此处空位,而径直落向X-H所构成的p型势阱空位。所以FPH2⋯FH中 P⋯F之间才有键临界点。
这里,认为X、Y都为电负性高的原子对氢键形成有利的认识还是正确的,Y电负性高,在其成键中得到较多的电子,其上的n电子(或单电子、π电子等)的能级被抬得更高;X电负性高,它的成键能级低,其成键的外围空域π*或者σ*也相应更低。这样一更高、一更低,形成氢键时偏移电子会更多,形成氢键时电子能量下降更大、氢键会更强。在这个过程中,Y的p型电子偏移走了电子,电子排斥减小、能级下降、电负性提高,而X处的p型势阱空位增加电子,电子排斥增加、能级上升、电负性降低,形成氢键的双方达到电负性均衡,能级均衡,组成统一的MO。
蓝移氢键的情形,上述氢键通式不够用了,需要扩充为Z≈X-H⋯Y。这里,X处还是中心。Z可以认为是另一个Y,Z的n电子在分子中也要向X处的外围空域π*或者σ*偏移电子。这时需要Z的电负性比X高,这是n型蓝移氢键。≈代表Z与X的多键或者多重键的连接,这样就把v型蓝移氢键也概括进来了,这时没有n电子,只有键电子之间的Pauli排斥、范德华作用的排斥。在这个形成蓝移氢键过程中,导致了相关原子的重杂化、重极化,超共轭变化,键长变化。
上述都有一个单独的氢键MO,它本是Y上的n电子向X-H的空间势阱排布了一点电子形成的,而且这n电子的母体与抛出的子体是反相位的,中间有节面。
还有,如果说通常形成共价键是双方电子往键中间转移了部分电子,双方都因电子部分转移走了而能级双双下降。氢键则是一方电子偏移走了能级下降,另一方从真正的没有电子占据时的LUMO [1] 接受电子能级升高,双方达到均衡。这和母体与抛出的子体反相位都是氢键形成的MO的特点,而且无论分子间的Y与X-H,还是分子内Z与X-H,所形成的氢键都是这样。
如今,尽管H已经不在中心位置了,不再需要质子的给、受这一说,但我们仍说上述这一切情形为“氢键”。正如科学早已认识到人不是用心脏来思考的,但我们还是说心思、心想等等,这已经成为人所共知的历史习惯、成为文化了。一提氢键,相关的体系构成就都明白了,一切都可以约定成俗。但关注的关键点、概念不一样了。
事实上,历来对氢键所有立足于理论计算的具体正确结果,都必然可以包含在氢键新概念Z≈X-H⋯Y之中。只是由这些计算结果升华的认知,以往囿于氢键是质子的给、受,一直对许多氢键特别是蓝移氢键的机理说得不那么真切。比如把蓝移氢键的各种特征变化说成是蓝移氢键的机理,而不能说明这各种特征变化是怎么导致的。
许多对分子氢键的电子密度ρ的拓扑研究,得到了氢键以及蓝移氢键的客观存在的种种特征,无疑都是合理的,可用的。只是它们离开了MO,对这种种特征的根源还是说不真切,因为从MO到电子密度ρ,失去了电子作为波的最原始的相位信息。
3.2. 关于氢键的量子化学计算方法 [15] - [17]
在氢键新概念中,关键在于认定形成氢键的那个Y的孤对电子n(或者单电子、π电子等)是向X-H处的反键空域转移了部分电子,形成一个氢键轨道。
在氢键通式X-H⋯Y,这时不能把X-H处的电子数值认为是参与轨道相互作用X-H自身的,而要理解成为Y的n电子要进入X-H的反键空域π*或者σ*,需要采取X-H处的势阱,描述这空域势阱的基组线性组合是X-H的,电子却是Y的n转移过来的。不能设想一个孤对电子n能与价键的饱和配对键电子X-H发生轨道相互作用、发生组合形成新的MO。
HF方法考虑了基于Pauli互斥的“交换相关”,使具有平行自旋的电子在空间中天然地存在相互回避,平均距离拉开。
然而HF方法没有考虑即使在一个MO上的两个反平行自旋的电子,在空间中也会天然地存在相互回避,平均距离拉开。好像是每个电子周围有一个禁区,当两个电子禁区相互重叠就会彼此避让,这个
就是“关联穴”。此即库伦相关,也即量子化学说的“电子相关”。
HF方法计算一个电子时认为是它与所有电子的平均场之间的作用,不能充分考虑这种反平行自旋的电子在空间相互回避的天然地客观存在,把这种并不可能存在的情形也计算在内了,因此使得电子出现得太密、电子之间的排斥过大。
这种偏差在post-HF方法得到补偿、校正,使电子分布不那么紧密、更加舒展一些,这本就是配对电子在空间分布的一种天然客观存在。
量子化学计算实践表明,HF方法尽管没有考虑电子相关,计算氢键在定性上还是基本靠谱的,与post-HF方法计算的结果在性质上是一致的,因为Y的n电子是偏移向π*或者σ*空域,是一个n电子的自身排布问题,在电子排布的大体上还没有出现大的问题。
然而HF方法计算蓝移氢键就不那么合用了,因为这里还出现了配对电子之间的排斥,不考虑电子相关就不能精确计算这种排斥。HF方法计算范德华作用就不合用了,因为范德华作用的本质是分子的价键配对电子之间的作用,情况更为复杂了。
对于蓝移氢键,如果将概念再升华、再往高里概括,n型蓝移氢键、v型蓝移氢键就都统一起来了。在n型场合,恰是Y与Z具有相同自旋的电子在X-H处势阱空间相遇,在v型场合,Y与Z处的配对键电子在氢键锚定的中程空间相遇,它们会相斥、排挤,使Z处的配对电子有点顺势退避,这都是Pauli互斥的静电作用的层次。这静电作用层次的电子分布,进一步还要经过量子层次的电子相关处理,以便完整精确地表达客观存在的电子分布。在post-HF方法计算的实际操作中也正是在HF方法计算的基础上进行电子相关校正,将本来不存在的具有反平行自旋的电子在空间中还同时在同一处存在的情形剔除掉,使电子分布更加合理、符合客观实际。
3.3. 关于电子相关的Δρ图像考察
可以将post-HF方法与HF方法分别计算几个典型的例子并作它们的全电子密度差Δρ,来直观查看电子相关的方法在电子密度分布上,具体有着什么样的校正以及它的意义。
这里,post-HF方法具体采用的是CCSD/aug-cc-pVTZ,HF方法所使用的基组与之相同。这几个例子里取的键长都是CCSD优化出来的,它表明CCSD与HF方法电子在空间分布上的不同。其实对于通常共价键分子,CCSD与HF方法二者优化键长差距数量级(0.01Å)与它们在空间电子云分布图形尺寸数量级(几Å)差距巨大,键长对电子云影响可以忽略不计。
几个典型的例子:
第一,H2分子例子。两种方法算的全电子密度相差Δρ见图6(a)。等值线起始值取±0.0001。(用几何级数来生成等值线,步长为2,虚线为ρ减少的区域,实线为ρ增加的区域,下同)
大家最熟悉的是H2分子与组成它的两个自由H原子的电子密度差Δρ,电子往键中间增加聚集形成成了共享电子,CCSD中间聚集增加了0.2478,HF方法也大约是这样,它们Δρ具有同样的图像、性质。
图6(a)是CCSD与HF两种方法分别算H2的全电子ρ做的Δρ,它表明CCSD的电子在键中间排布有少量减少,电荷减少了0.01374,增加到两核的外边了。HF方法算的H2总能量为−1.133056,CCSD算的总能量为−1.172587,而H2总能量实验值为−1.174。可见由于没有考虑电子相关,HF方法把反平行自旋的电子在空间同在一处几率不大的情形计算得几率过高了,以至高估了电子之间的排斥,使得体系总能量偏高。当然,它们的电子都往核之间聚集了,只是聚集的程度相差了0.01374电子。
H2的这两种方法相差的情形和图像在共价键是个典型代表。在共价键的情况下,电子往键中间增加了聚集,只是post-HF方法聚集得更合理些、更符合客观实际些。可见即使是一个共价键的MO也需要考虑电子相关才能得到精确计算。
第二,HF分子例子。两种方法算的全电子密度相差Δρ见图6(b)。等值线的起始值取±0.00002。
图6(b),两种方法相比较,一方面表现了HF分子像H2那样,电子在键中间减少了,安排到键两端的外面了。另一方面,F上与这个键垂直正交的孤对电子的分布也往外延伸了,HF方法则安排得过于收缩。此外,经验判断HF方法H往F上转移的电子计算量也过多了一点。
第三,He二聚体的范德华作用体系例子。用两种方法分别作的全电子密度相差Δρ见图6(c)。等值
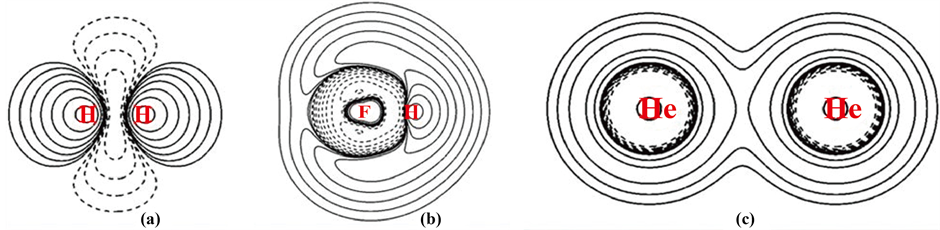
Figure 6. H2(A), HF(B), He dimer(C) of the CCSD density minus the HF density Δρ figure
图6. H2(A)、HF(B)、He二聚体(C)的CCSD密度减去HF密度的Δρ图
线起始值取±0.00001。
图6(c)表明,两种方法相比较,一方面两个具有配对电子的He在这样的距离,由于电子的Pauli互斥,电子转移到二He的背后和周边了,近核处电子显著减少。另一方面,二He核之间却有电子聚集显著增加。
不是说二He核之间是配对电子的Pauli互斥吗,为什么电子反倒会在核间聚集?
我们说配对电子的Pauli互斥,只是说的配对电子与配对电子之间的互斥作用,它并没有直接明确涉及到核,实际上Pauli互斥的电子总是处于核势场之中的。当两个配对电子的体系相遇、相碰时,因排斥部分电子从正面转移到核(或者配对电子所在的键)的背后,随之而来的是面对面较裸露核之间排斥和双方电子排斥会拉开核的距离。当双方拉开至范德华长程距离时,排斥迅速减小,量变引起质变,双方相对比较裸露的核处吸引电子能力的增强却凸显出来了,电子反而会重新聚集在双方较裸露的核之间,形成了在核之间低势阱处共享电子的增加,共享电子又主要布居在二核之间,直接减小了核与核之间的排斥,从而抗衡了双方的配对电子之间的排斥和较裸核之间的排斥,达到平衡,形成了所谓范德华作用。图像在核之间共享电子的增加正反映了范德华作用的本质。计算得到电子转移到二He的背后和中间共享电子的增加共计0.01099个电子。二核近核处电子则减少了这个数字。从总的电子变化划分出的共享电子的数量级应是与范德华作用大小的数量级相匹配的。
现在的Δρ把两种方法之差定量地图示出来了:HF方法因电子安排得过密始终只有排斥,完全不能用来描述范德华作用。只有考虑电子相关的post-HF方法,才能计算出核裸露时核之间重新聚集电子的范德华作用。
图6(c)展示的He2电子在核间的重新聚集的图景是简单而典型的,所有范德华作用体系都有这样的电子在核间(键间)的重新聚集共享的图景,它就是范德华作用的摄像,这就是范德华作用的机理。
共价键、氢键和范德华作用,形成引力的都是不同来源不同数量的电子共享,有着共同的化学本质。
一个比较简单、近似的分离范德华作用和其它作用的方法是:用post-HF方法计算的相互作用能减去HF方法计算相互作用能。GAMESS-US的LMOEDA能量分解方法给出色散作用能就是用的这个做法。色散作用属于范德华作用。称为色散,因为计算电子相关色散校正的基本思想和方法是从光的色散搬过来的。显然,这个能量分解方法还是有片面性的,因为电子相关是全分子、全体系的,范德华作用只是分子体系之间局部配对电子的作用。图6(a)、图6(b)都作了色散校正,能量都有所降低,但这里并没有范德华作用的引力出现。
至此,还需要进一步区分一下电子相关色散校正与范德华作用的区别。电子相关的色散校正,是把HF方法计算的分子内所有配对电子在同一个位点出现反平行自旋的电子的分布情况剔除了,这本就是不存在的,它对整个化学体系的任一处电子分布都是适用、要应用的。
由于色散校正使电子的布居更加符合客观存在,色散校正使得某分子的电子在受到其它分子的核的吸引而降低能量时,避免与其它分子上电子距离可能瞬时较近带来的较大互斥,因此净效果令总体能量降低,从而在这个基础上能够较好地计算范德华作用,即在分子间局部相遇、相碰时,能够正确计算在配对电子的Pauli互斥的情况之下,核之间还能重新聚集共享电子产生引力。而HF方法算的配对电子相遇永远只有排斥。因此不能认为电子相关色散校正提供了计算范德华作用的基础,就认为范德华作用就是电子相关色散校正。
电子相关色散校正只是配对电子在空间排布的问题,范德华作用是相遇相碰的配对电子在核势场中的空间排布还会重新在核之间有聚集,电子分布在核之间产生了新的作用新的质,这是不同层次的两件事,范德华作用是单纯的电子相关色散校正所不能概括的,尽管范德华作用时的电子也是经过色散处理的。不能因为考虑了电子相关色散校正之后能够计算范德华作用了,就认为色散校正就是范德华作用。可见,如果把范德华作用说成是色散作用能,那么色散作用能与电子相关的色散校正也并不是一回事。
作为配对电子之间的范德华作用,能在核之间重新聚集一定量的共享电子以平衡排斥,既不能归结到Pauli互斥,也不能归结到电子相关。尽管一直都没有对范德华作用的本源给出一个真切的解释,但范德华却从实验得知了在饱和无极性价键分子之间还会产生引力,如今范德华作用还是一个独立存在的化学概念,具有独自的机理,有着广泛的领域。
3.4. 关于电子密度差Δρ用于氢键、蓝移氢键,以及范德华作用
Δρ在多种场合有多种形式可以运用,比如常用于分子体系整体的电子密度ρ减去组成分子的各原子在自由状态的ρ。但这种方法各个成键引起的电子变化比起氢键、范德华作用引起的电子变化要强烈得多,氢键、范德华作用引起的电子变化常被遮盖,不易从中识别。
分子间氢键以及有时还发生的蓝移情形,还有范德华作用,它们虽然形成了二聚体,相对组成二聚体的分子本身的刚性成键骨架来说,氢键、范德华作用毕竟是一个微小的变化。这个微小的变化,对双方刚性分子整体的影响也是微小的,但对灵动的电子云的排布却会发生可观的影响,从而通过这电子云排布的变化找到产生氢键、蓝移氢键、范德华作用的机理。
当我们用分子间氢键、范德华作用体系的电子密度ρ,逐一减去刚从氢键、范德华作用中独立出来(还取体系的构型尚未施豫)的两个单体电子密度ρ时,两个单体在二聚体中没有变化的刚性价键的电子密度ρ全部抵消了,只留下两个单体在二聚体中电子密度净变化Δρ。
比如垂直型二苯二聚体的Δρ,它的电子变化“一波三折”,充分反映了氢键电子转移这一波,以及引起的对右边的正面苯的电子变化传递余波,其它刚性骨架电子没有变化而抵消了。其实氢键轨道MO40,即图5(b),目前等值面取了0.07,只突出了氢键电子的转移。如果等值面取值0.01,则可在MO40也看到传递的余波。
对于范德华作用,这时还可以采用post-HF方法与HF方法分别计算电子密度来作差,拿完全没有范德华作用的HF方法作为背衬,作的Δρ可以看到这时的电子在核间重新聚集情况,看到范德华作用。
对于氢键,则不必用两种方法来作Δρ,因为这时体系的价键的电子密度变化在图像上的表现还比氢键更强烈,氢键引起的电子变化反倒会被掩没。这时还是用氢键体系与构成氢键的双方作Δρ更明晰些,刚性骨架的价键电子基本被抵消了,看见的只是氢键引起的电子净变化。
电子密度差Δρ应是传统在分子中求原子净电荷(Mullkin方法 [18] )的当代发展。Δρ并不局限于分子中的原子,而是分子中在形成氢键、范德华作用体系前后各分子以及各片区的电子净变化,更加合理、更符合客观实际。特别适用于氢键、范德华作用体系的计算研究。
原生态高精度的y(或ρ)一旦用等值面、等值线以图形将Δρ表达出来,肉眼看过去其实只是一个定性的图像,但这图像却在更高的层次上展现了新的质,正是这新的质可以揭示共价键、氢键和范德华作用机理的本源信息。
致谢
卢天博士对量子化学计算和文献给予了指导,对此研究工作进行了讨论,特此致谢!
文章引用
周光耀. 氢键的量子化学研究(二)
A Quantum Chemistry Study of Hydrogen Bonds (2)[J]. 物理化学进展, 2016, 05(02): 58-74. http://dx.doi.org/10.12677/JAPC.2016.52007
参考文献 (References)
- 1. 周光耀. 氢键的量子化学研究(一) [J]. 物理化学进展, 2015(4): 84-101.
- 2. Hobza, P. and Havlas, Z. (2000) Blue-Shifting Hydrogen Bonds. Chemical Reviews, 100, 4253-4264. http://dx.doi.org/10.1021/cr990050q
- 3. Hobza, P. and Havlas, Z. (2002) Improper Blue-Shifting Hydrogen Bond. Theoretical Chemistry Accounts, 108, 325- 334. http://dx.doi.org/10.1007/s00214-002-0367-5
- 4. 周盼盼. 分子间弱相互作用体系的理论研究: 氢键、范德华相互作用和卤键[D]: [博士学位论文]. 兰州: 兰州大学, 2010.
- 5. Kseniya, M., Leonid, K., Jan, L., Alexandra, D. and Markku, R. (2010) Matrix Isolation and Ab Initio Study of Trans- Trans and Trans-Cis Dimers of Formic Acid. The Journal of Physical Chemistry A, 114, 3495-3502. http://dx.doi.org/10.1021/jp911515f
- 6. Lu, T. and Chen, F.W. (2012) Multiwfn: A Multifunctional Wavefunction Analyzer. Journal of Computational Chemistry, 33, 580-592. http://dx.doi.org/10.1002/jcc.22885
- 7. 闫秀花, 黎安勇, 王素纹, 苗树青. 双接触蓝移氢键PH2…Y的理论研究[J]. 西南大学学报(自然科学版), 2008(30): 25-31.
- 8. 倪杰. 分子内超共扼对于氢键性质的影响[D]: [硕士学位论文]. 重庆: 西南大学, 2009.
- 9. 周光耀. 范德华作用的量子化学研究(一) [J]. 物理化学进展, 2013(2): 21-26.
- 10. Hobza, P. and Sypirko, V. (1998) An-ti-Hydrogen Bond in the Benzene Dimer and Other Carbon Proton Donor Complexes. The Journal of Physical Chemi-stry A, 202, 2501-2504. http://dx.doi.org/10.1021/jp973374w
- 11. Sławomir, J.G. (2006) Hydrogen Bonding-New Insights. Challenges and Advances in Computational Chemistry and Physics, Volume 3, Springer, Dordrecht.
- 12. 张翼, 杨颙. 氢键研究进展[J]. 化学教育, 2007(2): 7-9.
- 13. 王海燕, 曾艳丽, 孟令鹏, 郑世钧. 有关氢键理论研究的现状及前景[J]. 河北师范大学学报(自然科学版), 2005(29): 177-181.
- 14. 纪爱萍. 蓝移氢键起因的理论计算研究[D]: [硕士学位论文]. 济南: 山东师范大学, 2008.
- 15. 吴军, 涂宏庆, 崔云康, 唐春红. 氢键的量子化学研究方法[J]. 计算机与应用化学, 2015(32): 903-906.
- 16. Hobza, P. and Zahradnik, R. (1988) Intermolecular Interactions between Medium-Sized Systems. Nonempirical and Empirical Calculations of Interaction Energies: Successes and Failures. Chemical Reviews, 88, 871-897. http://dx.doi.org/10.1021/cr00088a004
- 17. Li, X., Liu, L. and Schlegel, H.B. (2002) On the Physical Origin of Blue-Shifted Hydrogen Bonds. Journal of the American Chemical Society, 124, 9639-9647. http://dx.doi.org/10.1021/ja020213j
- 18. James, B.F. and Eleen, F. (1996) Exploring Chemistry with Electronic Structure Methos. 2nd Edition, Gaussian Inc., USA.