Journal of Advances in Physical Chemistry
Vol.07 No.03(2018), Article ID:26632,5
pages
10.12677/JAPC.2018.73018
Crystal Structure and Hydrogen Storage Properties of Kalium Hydride from Theoretical Calculations
Guanghui Lin, Qian Zhao, Yun Liu, Jiehong Lei*
Physics and Space Science of Institute, West China Normal University, Nanchong Sichuan

Received: Aug. 9th, 2018; accepted: Aug. 22nd, 2018; published: Aug. 29th, 2018

ABSTRACT
The physical properties of potassium hydride isotope compounds (KHxD1−x, KHxT1−x, KDxT1−x; x = 0, 0.25, 0.5, 0.75, 1.0) were calculated by the density functional theory method using plane wave pseudopotential combined with generalized gradient approximation, including lattice constant, density, and density of H(D)T. The calculation results show that the lattice constant and density of KH(D,T) are very close to the experimental values; as the value of x increases, the lattice constant hardly changes and the density decreases. The calculated DT density in KD0.25T0.75 is about 0.13 g/cm3, which shows good hydrogen storage performance.
Keywords:Density Functional Theory, Crystal Structure, Hydrogen Storage Properties, Kalium Hydride
氢化钾晶体结构与储氢性能的理论计算
林光会,赵倩,刘芸,雷洁红*
西华师范大学物理与空间科学学院,四川 南充

收稿日期:2018年8月9日;录用日期:2018年8月22日;发布日期:2018年8月29日

摘 要
运用平面波赝势结合广义梯度近似的密度泛函理论方法计算了氢化钾同位素化合物(KHxD1−x, KHxT1−x, KDxT1−x; x = 0, 0.25, 0.5, 0.75, 1.0)的物理性质,包括晶格常数、密度及H(D)T的密度。计算结果显示KH(D,T)的晶格常数和密度与实验值非常接近;随着x值增加,晶格常数几乎没有发生变化,而密度减小。KD0.25T0.75中DT密度的计算值大约为0.13 g/cm3,表现出了良好的储氢性能。
关键词 :密度泛函理论,晶体结构,储氢性能,氢化钾

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着化石燃料越来越少,人们正在寻找新能源来补充或替换正常能源。氢作为一种储量丰富的能源,被人们广泛认为是一种潜在的理想能源 [1] [2] [3] [4] 。许多金属和合金能够可逆地吸收大量的氢 [5] [6] [7] [8] 。碱金属如锂、钾和钠能与氢反应生成类似KCl的结构。这些氢化物具有氢密度大、原子序数小等特点,被许多人研究 [9] [10] 。我们已经证明了LiDxT1−x可以提高融合燃料容量不增加体积或充电点火目标的通胀压力在LiDxT1−xDT的密度等于DT冰 [11] 。由于氢化钾与氢化锂具有相同的性质,本文将研究氢化钾的晶体结构和储氢性能。到目前为止,科学家们主要研究了KH (氢化钾),KD (氘化钾)和KT (氚化钾)的性质,如晶格常数和密度 [12] [13] [14] [15] 。然而,几乎未见有对KHxD1−x,KHxT1−x,KDxT1−x的晶格参数、密度研究的公开报道,缺乏晶格常数、密度的数据。而系统研究x值对密度影响尚属首次。
2. 理论方法
本文的计算是基于密度泛函理论的第一性原理方法,利用MS4.1软件中的量子力学模块CASTEP软件包完成 [16] [17] 。在CASTEP软件包中,采用掺杂的方式 [18] 构建了KHxD1−x,KHxT1−x,KDxT1−x (x = 0, 0.25, 0.5, 0.75, 1.0)的晶体结构,运用平面波赝势结合广义梯度近似的密度泛函理论方法来优化不同x值的晶体结构,得到晶格常数。交换相关函数是GGA-RPBE [19] ,电子和离子间的相互作用采用超软赝势采用超软心赝势(ultrasoft) [20] ,几何优化计算的精确性由下面的条件控制:能量偏差5.0 × 10−6e V/atom;计算使用的截止能是330 eV;布里渊区积分采用Monkhorst-Pack形式的特殊K点方法,使用了6 × 6 × 6个特殊K点。
3. 结果与讨论
利用CASTEP软件包构建KHxD1−x,KHxT1−x,KDxT1−x (x = 0, 0.25, 0.5, 0.75, 1)结构。显然,三钾氢同位素化合物具有面心立方对称。K原子占据(0, 0, 0)网点和H(D,T)原子占据±(1/2, 1/2, 1/2)网点。
我们对晶格参数进行了优化。在下面的计算中,使用了优化结构。首先计算了零压力下的平衡体积,然后计算了单元中所有原子的总质量或H(D,T)的质量。最后,密度可以确定。
平衡晶格常数和氢化钾密度可以通过公式(1)计算得出。它们与其他理论值一起列于表1中。
(1)
其中,M指晶体一个单胞中原子的总质量,V指单胞的体积,由于KH、KD(KT)晶体都属于面心立方结构,故 。
晶格常数和密度的计算值与其它理论值接近,说明计算方法可行,结果可靠。
用同样的方法计算了三元氢化钾同位素的晶格常数和密度。这些数据列于表2中。
从表2中可知,不同x值下的KHxD1−x,KHxT1−x和KDxT1−x晶格常数变化非常小,这可能是因为H及其同位素的原子半径变化小的原因。密度随x值的变化关系见图1。可以看出x值相同时,KHxD1−x的密度值最小,KHxT1−x的密度值居中,KDxT1−x的密度值最大;且随着x值的增大,它们的密度都减小。这是因为x值几乎对晶格常数没有影响,而x值不同,晶体中掺杂的H同位素不同,原子量发生了变化,这就使得公式(1)中,V值无变化,M值发生变化,从而使得密度ρ变化。
从上述方法可知,要计算KHxD1−x,KHxT1−x和KDxT1−x中HT、HD和DT的密度值,只需将公式(1)中的M代换为一个原胞中H(D)、T原子的总质量即可。KHxD1−x,KHxT1−x和KDxT1−x中HT、HD和DT的密度值随x的变化关系如图2所示。
Table 1. Comparison of lattice constants, densities and experimental values of KH (KD, KT)
表1. KH (KD, KT)晶格常数,密度与实验值的比较
Table 2. Lattice constants and density values of three potassium hydride isotopes with different x values
表2. 不同x值的三元氢化钾同位素化合物晶格常数和密度值
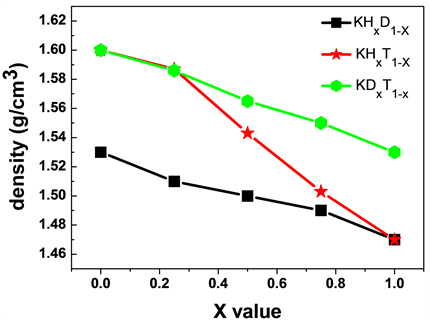
Figure 1. The relationship between the density value of three potassium hydride isotope compounds and the x value
图1. 三元氢化钾同位素化合物密度值随x值的变化关系

Figure 2. H(D)T density under different x values
图2. 不同x值下的H(D)T密度
从图2中可以看出,x值相同时,KHxD1−x的HD含量最少,KHxT1−x的HT含量居中,KDxT1−x的DT含量最大;随着x值的增加,H(D)T密度减小。对于KDxT1−x,计算的结果显示它其中的DT密度值较大,大约为0.136 g/cm3,这个值小于激光惯性约束聚变中DT冰的密度,但它具有优良的储氢性能。
4. 结论
我们采用掺杂的方式构建KHxD1−x,KHxT1−x和KDxT1−x (x = 0, 0.25, 0.5, 0.75, 1.0)的晶体结构,运用平面波赝势结合广义梯度近似的密度泛函理论方法计算了x = 0, 0.25, 0.5, 0.75, 1.0时,它们的晶格常数、密度值及其H(D)T的密度值。计算结果显示KH(D, T)的晶格常数和密度与实验数据符合的很好。首次通过理论计算得到了KHxD1−x,KHxT1−x和KDxT1−x (x = 0.25, 0.5, 0.75)的晶格参数、密度的数据,这是研究金属氢化物储氢材料的储氢性能的一个重要理论基础。
基金项目
四川省科技厅应用基础研究面上项目(2017JY0145)。
文章引用
林光会,赵 倩,刘 芸,雷洁红. 氢化钾晶体结构与储氢性能的理论计算
Crystal Structure and Hydrogen Storage Properties of Kalium Hydride from Theoretical Calculations[J]. 物理化学进展, 2018, 07(03): 147-151. https://doi.org/10.12677/JAPC.2018.73018
参考文献
- 1. Sakintuna, B., Lamari-Darkrim, F. and Hirscher, M. (2007) Metal Hydride Materials for Solid Hydrogen Storage: A Revies. Interna-tional Journal of Hydrogen Energy, 32, 1121-1140. https://doi.org/10.1016/j.ijhydene.2006.11.022
- 2. Orimo, S., Nakamori, Y., Eliseo, J.R., et al. (2007) Complex Hydride for Hydrogen Storage. Chemical Reviews, 107, 4111-4132. https://doi.org/10.1021/cr0501846
- 3. Satyapal, S., Petrovic, J., Read, C., Thomas, G. and Ordaz, G. (2007) The US Department of Energy’s National Hydrogen Storage Project: Progress towards Meeting Hydrogen-Powered Vehicle Requirements. Catalysis Today, 120, 246-256. https://doi.org/10.1016/j.cattod.2006.09.022
- 4. Lohstroh, W., Fichtner, M. and Breitung, W. (2009) Complex Hydrides as Solid Storage Materials: First Safety Tests. International Journal of Hydrogen Energy, 34, 5981-5985. https://doi.org/10.1016/j.ijhydene.2009.01.030
- 5. Graetz, J. (2009) New Approaches to Hydrogen Storage. Chemical Society Reviews, 38, 73-82. https://doi.org/10.1039/B718842K
- 6. Schlapbach, L. and Zuttel, A. (2001) Hydrogen-Storage Materials for Mobile Applica-tions. Nature, 414, 353-358. https://doi.org/10.1038/35104634
- 7. Bloch, J. and Mintz, M.H. (1997) Kinetics and Mechanisms of Metal Hydrides For-mation—A Review. Journal of Alloys and Compounds, 253, 529-541. https://doi.org/10.1016/S0925-8388(96)03070-8
- 8. Van den berg, A.W.C. and Areán, C.C. (2008) Material for Hydrogen Storage: Current Research Trends and Perspectives. Chemical Com-munications, 6, 668-681. https://doi.org/10.1039/B712576N
- 9. George, L. and Saxena, S.K. (2010) Structural Stability of Met-al Hydrides, Alanates and Borohydrides of Alkali and Alkali-Earth Elements: A Review. International Journal of Hydrogen Energy, 35, 5454-5470. https://doi.org/10.1016/j.ijhydene.2010.03.078
- 10. Pandey, J.D. (1978) Properties of Isotopic Lithium Hydride in Crystalline State. Journal of Inorganic and Nuclear Chemistry, 40, 1184-1185. https://doi.org/10.1016/0022-1902(78)80537-5
- 11. Lei, J.H., Duan, H. and Xing, P.F. (2010) Calculation of the Physical Properties of an Isotopic Compound of Ternary Lithium Hydride. Physica Scripta, 82, 5607-5610.
- 12. Magg, U. and Jones, H. (1988) The Ground-State Infrared Spectrum of Sodium Hydride. Chemical Physics Letters, 146, 415-418. https://doi.org/10.1016/0009-2614(88)87469-4
- 13. Smithson, H., Marianetti, C.A., Morganm, D., et al. (2002) First-Principles Study of the Stability and Electronic Structure of Metal Hydrides. Physical Review B, 66, 4107-4116. https://doi.org/10.1103/PhysRevB.66.144107
- 14. Maki, A.G. and Olson, W.B. (1989) Infrared Spectrum of Sodium Hydride. The Journal of Chemical Physics, 90, 6887-6892. https://doi.org/10.1063/1.456263
- 15. Bowman, R.C. (1973) Thermal Expan-sion Coefficients of Lithium Hydride. Journal of Physics and Chemistry of Solids, 34, 1754-1756. https://doi.org/10.1016/S0022-3697(73)80143-X
- 16. Payne, M.C., Teter, M.P., Allen, D.C., Arias, T.A. and Joannopoulos, J.D. (1992) Iterative Minimization Techniques for Ab Initio Total-Energy Calculations: Molecular Dynamics and Conjugate Gradients. Re-views of Modern Physics, 64, 1045-1077. https://doi.org/10.1103/RevModPhys.64.1045
- 17. Guo, Y.D., Cheng, X.L., Zhou, L.P., et al. (2006) First-Principles Calculation of Elastic and Thermodynamic MgO and SrO under High Pressure. Physica B, 373, 334-340. https://doi.org/10.1016/j.physb.2005.12.244
- 18. Hammer, B., Hansen, L.B. and Norskov, J.K. (1999) Improved Ad-sorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerh of Functionals. Physical Review B, 59, 7413-7421. https://doi.org/10.1103/PhysRevB.59.7413
- 19. Vanderbilt, D. (1990) Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism. Physical Review B, 41, 7892-7895. https://doi.org/10.1103/PhysRevB.41.7892
- 20. Perdew, J.P., Burke, K. and Ernzerhof, M. (1996) Generalized Gradient Approximation Made Simple. Physical Review Letters, 77, 3865-3868. https://doi.org/10.1103/PhysRevLett.77.3865
NOTES
*通讯作者。
