Journal of Water Resources Research
Vol.06 No.04(2017), Article ID:21345,8
pages
10.12677/JWRR.2017.64040
Vulnerability Assessment of Torrent Flood Disasters Based on Variable Fuzzy Comprehensive Evaluation Method
Huimin Liu, Kuan Liu, Wenchuan Wang*, Dongmei Xu
College of Water Conservancy, North China University of Water Resourses and Electric Power, Zhengzhou Henan

Received: Jun. 22nd, 2017; accepted: Jul. 4th, 2017; published: Jul. 12th, 2017

ABSTRACT
The vulnerability of mountain torrents refers to the ability of people to resist and cope with floods and the ability to recover from adverse effects after suffering from floods. In this paper, the variable fuzzy comprehensive evaluation model is established by comprehensively considering the hydrological indicators and economic development of Harbin. The comprehensive evaluation of the vulnerability of mountain flood disaster of 12 counties (cities, district) are carried out by selecting 12 disaster vulnerability indicators, and using the analytic hierarchy process to determine the index weights. The variable fuzzy comprehensive evaluation method takes into account the influence of the evaluation standard interval value on the evaluation results and carries out the comprehensive evaluation under the four combinations of parameters to improve the credibility and reliability of the vulnerability assessment results, which has practical significance.
Keywords:Vulnerability Assessment, Analytic Hierarchy Process, Variable Fuzzy Comprehensive Evaluation, Disaster Mitigation
基于可变模糊综合评判法的山洪灾害脆弱性分析
刘惠敏,刘宽,王文川*,徐冬梅
华北水利水电大学水利学院,河南 郑州

收稿日期:2017年6月22日;录用日期:2017年7月4日;发布日期:2017年7月12日

摘 要
山洪灾害脆弱性是指人们抵抗和应对洪灾的能力以及在遭受洪灾后从不利影响中恢复的能力。本文综合考虑哈尔滨市水文指标及经济发展现状,选取12项灾害脆弱性指标,采用层次分析法确定指标权重,建立可变模糊综合评判模型,对哈尔滨的12个县(市、区)进行山洪灾害脆弱性综合评价。建立的模型考虑了评价标准区间值对评价结果的影响并进行了四组组合参数下的综合评价,提高了脆弱性评价结果的可信度和可靠性,对哈尔滨市山洪灾害减灾抗灾具有现实意义。
关键词 :脆弱性分析,层次分析法,可变模糊综合评价,减灾抗灾

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着全球气候变暖、城市化加剧、人口增加、经济高速发展,洪涝灾害发生的强度、频度和广度不断增加,已成为社会经济可持续发展的严重制约因素。我国在山洪灾害脆弱性研究方面起步较晚,理论方法尚不成熟,代表性案例的研究较少。2002年,刘兰芳 [1] 运用极差标准化模型对洪涝灾害脆弱性定量评估并分析其分布规律。2003年,汪朝辉 [2] 等在构建极差标准化模型计算脆弱度的基础上,利用GIS技术进行时空分异表达。2005年,葛怡 [3] 改进了Hoovering评估模型并对长沙地区进行了水灾社会脆弱性的评估。2010年,刘毅 [4] 引入应用数据包络分析(DEA)投入产出模型对全国范围的自然灾害脆弱性进行区域特征分析。2016年,何亚伯 [5] 提出了运用改进DEA交叉效率模型和熵权法相结合的洪水灾害区域脆弱性评价方法,具有较好的适用性。由于山洪灾害涉及到的众多影响因子之间存在非同一性、随机性和模糊性,简单的数学方法得到评价结果反映实际情况时不够客观。为提高评价结果的可信度和可靠性,本文采用陈守煜教授创立的可变模糊集理论 [6] 中的可变模糊评价法,对哈尔滨市各评价对象进行变化模型参数组合综合分析,判断评价对象所处脆弱等级。
暴雨洪涝灾害是黑龙江省主要的自然灾害之一,对当地经济发展尤其是农业生产及生态环境具有较大影响,哈尔滨市属于暴雨洪涝灾害高发区,地均GDP高、人口密度大、易损性指数高、风险较大。因此,对哈尔滨市县域脆弱性分析,为进一步研究哈尔滨市洪水灾害风险评价具有重要意义。哈尔滨市地处东北亚中心地带,除双城区、呼兰区地势平坦低洼,东部县市多为山区丘陵。本文以哈尔滨市的12个县(市、区)为研究对象,对哈尔滨市山洪灾害脆弱性进行评价。
2. 指标体系构建及权重确定
2.1. 构建指标体系
指标体系的构建要具有科学性、可操作性、独立性、简明性和系统性。山洪灾害脆弱性不仅包含气候、地貌、地层岩性等自然环境的脆弱性,还包括经济、社会等以人为中心的脆弱性评价。即在山洪灾害爆发时,人类的应对能力和灾后重建及恢复能力。
植被覆盖率指森林面积占土地总面积的比例,它与脆弱程度有很好的相关关系 [7] 。平均坡度是各个子流域坡度的平均值,坡度值越高,汇流时间越短,越容易发生山洪灾害。土地利用现状分为水域及水利设施用地、房屋建筑(区)、耕地、草地和林地、沼泽等未利用土地五级,其脆弱性依次为最脆弱、较脆弱、脆弱、轻度脆弱、微脆弱 [8] 。土地利用现状指标的计算公式如下:
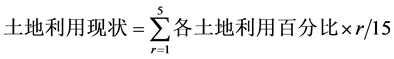 (1)
(1)
式中: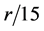 为各土地利用的权重。
为各土地利用的权重。
经济指标反映了区域抵抗灾害和灾后重建及恢复能力的大小,因此经济指标与山洪灾害脆弱性呈负相关。医院、卫生院床位数反映区域的医疗水平,床位数越多,对受灾群众的救助能力越强,暴雨洪涝灾害脆弱性越低,二者呈负相关。在校学生数可以反映该地区的教育水平,其计算方法为中小学在校学生总数与年末常住人口的百分比。重点防治区的个数是黑龙江省山洪灾害调查评价县级合同中对沿河村落进行详查的个数。砖木、钢筋混凝土结构住房面积比重大,对抗山洪灾害打击的能力就高,因此与暴雨洪涝灾害脆弱性呈负相关。以上数据的获得均来自哈尔滨市山洪灾害调查评价的实测或统计数据。
本文从承灾体属性和社会抗灾减灾能力两方面出发,选取了自然指标、经济指标、社会指标、敏感性指标4个一级指标,一级指标及各自对应的二级指标如表1。
Table1. Judgment matrix and weight distribution of vulnerability index in Harbin County
表1. 哈尔滨县域脆弱性指标判断矩阵及权重分布
2.2. 权重确定
指标权重大小体现了各指标对灾害脆弱性影响的强弱程度,科学合理的权重对于准确评价各地区的脆弱性具有非常重要的意义。常用的权重确定方法有专家打分法、层次分析法、主成分分析法、加权统计法、德尔菲法、回归分析法、熵值法等。本文采用层次分析法来计算评判过程中的权重分配。
层次分析法是一种定性与定量相结合的权重确定方法,其基本思路是把复杂问题中的各因素分解为互相影响和隶属的序层结构,使问题条理化 [9] 。每一层次均用定量的方法通过两两比较来表示各要素的相对重要性,然后利用综合评判确定各要素相对重要性排序。本文通过专家打分法把某一层中的要素和与高一层次某一准则的重要性进行两两比较,不同因子间的相互比较结果是根据T.L. Saaty [10] 的1~9标度方法进行打分,各层次两两比较重度矩阵见表1。
对一级指标判断矩阵及四个二级指标判断矩阵进行一致性检验,层次总排序一致性比例CR值依次为:0.038、0.009、0.047、0.015、0.009。当判断矩阵CR < 0.10时,说明判断矩阵具有令人满意的一致性。故一级、二级指标判断矩阵均满足一致性检验。
3. 基于可变模糊综合评判的山洪灾害脆弱性评价模型
可变模糊综合评价法能有效地解决标准区间值对综合评价结果的干扰,同时由于该方法考虑了评价模型参数的可变性,其评价结果能比较全面地反映各评价因子的作用。可变模糊综合评价法具体步骤如下 [11] :
(1) 洪水灾害脆弱性评价涉及多个级别,其标准值用区间数表示。已知待评价对象有n个,每个评价对象有m个评价指标,xij为第j个待评价对象的第i个指标(其中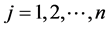 ,
,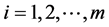 )。将评价指标i划分为k个
)。将评价指标i划分为k个
级别构造标准区间矩阵,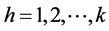 (h为标准区间矩阵的级别数)。标准区间矩阵为
(h为标准区间矩阵的级别数)。标准区间矩阵为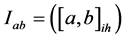 (b、a分别为模糊可变集合以吸引为主区间上的第h级别的最大、最小值)。
(b、a分别为模糊可变集合以吸引为主区间上的第h级别的最大、最小值)。
(2) 根据(1)中求得的k个危险等级的标准区间矩阵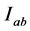 ,构造变动区间的范围值矩阵
,构造变动区间的范围值矩阵 (d、c分别为指标i第h级别的上、下边界)。
(d、c分别为指标i第h级别的上、下边界)。
(3) 根据标准区间矩阵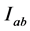 及各级别的物理分析与实际情况,确定山洪灾害评价指标i级别h的点值矩阵
及各级别的物理分析与实际情况,确定山洪灾害评价指标i级别h的点值矩阵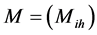 。本文采用
。本文采用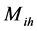 的点值通用模型进行计算。
的点值通用模型进行计算。
(4) 利用层次分析法及表1给出的指标判断矩阵数据计算指标权重确定脆弱性权重向量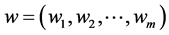 ,
,
其中 。各评价指标单排序权重及总排序权重见表1。
。各评价指标单排序权重及总排序权重见表1。
(5) 根据相对差异函数模型公式计算相对隶属度矩阵。
当xij落在Mih左侧,对于正向因子, ;对于逆向因子,
;对于逆向因子,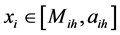 。相对隶属度求
。相对隶属度求
 (2)
(2)
当xij落在Mih右侧,对于正向因子, ;对于逆向因子,
;对于逆向因子,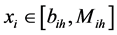 。相对隶属度求解公式为:
。相对隶属度求解公式为:
 (3)
(3)
(6) 利用下面的公式分别计算q、p四种不同组合情况下,研究对象j对于各级别的综合相对隶属度向量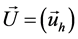 :
:
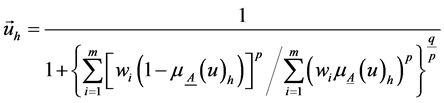 (4)
(4)
式中:q为模型优化准则参数,p为距离参数。Q = 1为最小一乘方准则,q = 2为最小二乘方准则;p = 1为海明距离,p = 2为欧式距离。
(7) 对综合相对隶属度向量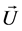 进行归一化处理,可得归一化综合相对隶属度向量
进行归一化处理,可得归一化综合相对隶属度向量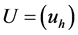 ,其中
,其中 。级别特征值公式为
。级别特征值公式为 (H为待评价单元的脆弱等级特征值)。
(H为待评价单元的脆弱等级特征值)。
4. 实例应用
本文研究对象为哈尔滨市12个县(市、区),每个待评价对象有12个指标因子,即m = 12。把研究对象的脆弱性等级分为极低、低、中等、高和极高5个脆弱等级,即k = 5。然后根据研究区的统计数据,在参考了国家、行业及地方规定或颁布的有关标准或文件基础上,利用点值矩阵通用模型,并结合实际情况确定各项评价指标的分级标准表2,可得出哈尔滨市山洪灾害脆弱性分析评价数据,见表3。
按照可变模糊综合评价步骤,对模型采取四种参数组合分别计算。求解出12个研究对象对于各级别的综合相对隶属度向量,并进行归一化处理。进而根据级别特征公式计算出各县(市、区)的脆弱级别特征值,计算结果见表4。
根据文献 [12] 中的脆弱等级判断标准可知:当H < 1.67时,脆弱性等级为一级,即极低脆弱等级;当1.67 ≤ H < 2.50时,脆弱性等级为二级,即低脆弱等级;当2.5 ≤ H < 3.50时,脆弱性等级为三级,即中脆弱等级;当3.50 ≤ H < 4.50时,脆弱性等级为四级,即高脆弱等级;当H ≥ 4.50时,脆弱性等级为五级,即极高脆弱等级。哈尔滨市12个评价对象的山洪灾害脆弱等级可变模糊综合评价结果如图1所示:
根据表4及脆弱等级判断标准,可变模糊综合评判法的计算结果如下,在选取的哈尔滨市12个县(市、区)中,2个评价对象的脆弱性等级为IV类,为高脆弱等级,分别为尚志市和通河县;8个评价对象的脆弱性等级为III类,为中等脆弱等级,分别为阿城区、巴彦县、宾县、方正县、木兰县、五常市、延寿县和依兰县;2个评价对象的脆弱性等级为II类,为低脆弱等级,分别为呼兰区和双城市。在极低脆弱等级和极高脆弱等级范围中没有研究对象分布。从图1可以看出,从西部到东部脆弱等级总体趋势由低变高。
Table 2. Analysis and evaluation criteria of vulnerability of torrent flood disaster in Harbin
表2. 哈尔滨市山洪灾害脆弱性分析评价标准
Table 3. Analysis and evaluation of vulnerability of torrent flood disaster in Harbin
表3. 哈尔滨市山洪灾害脆弱性分析评价数据
Table 4. Variable fuzzy analysis and evaluation results of vulnerability of torrent flood disaster in Harbin
表4. 哈尔滨市山洪灾害脆弱性可变模糊分析评价结果

Figure 1. Variable fuzzy analysis and evaluation results of vulnerability of torrent flood disaster in Harbin County
图1. 哈尔滨市县域山洪灾害脆弱性可变模糊评价研究结果
5. 结语
脆弱性分析评价是连接灾害与风险的重要桥梁,本文综合考虑自然、经济、社会和敏感性等多方面指标,利用可变模糊综合评判模型对哈尔滨市进行县域山洪灾害脆弱性评价,是区域山洪灾害脆弱性评价一条新的研究途径。研究表明脆弱性等级与当地经济发展水平具有明显的负相关关系,与平均坡度有明显的正相关关系。呼兰区经济较为发达且地势平坦,其脆弱性等级为II级;双城市虽然经济较为落后,但平均坡度为零,脆弱性等级也为II级;尚志市经济发展一般,且平均坡度值较大,脆弱性等级较高,为IV级;通河县坡度值中等水平,但经济发展较为落后,脆弱性等级也为IV级。综上,经济越发达越有利于抗震减灾及灾后重建,脆弱性等级就越低。因此,提高当地经济发展能力是降低脆弱性水平的重要方法之一。
基金项目
国家自然科学基金项目(51509088);水利部公益性行业科研专项(201501008),河南省高校科技创新团队(18IRTSTHN009)。
文章引用
刘惠敏,刘 宽,王文川,徐冬梅. 基于可变模糊综合评判法的山洪灾害脆弱性分析
Vulnerability Assessment of Torrent Flood Disasters Based on Variable Fuzzy Comprehensive Evaluation Method[J]. 水资源研究, 2017, 06(04): 332-339. http://dx.doi.org/10.12677/JWRR.2017.64040
参考文献 (References)
- 1. 刘兰芳, 邹君, 刘湘南. 农业洪涝灾害脆弱性成因分析及评估一以湖南省衡阳市为例[J]. 长江流域资源与环境, 2002, 11(3): 291-295. LIU Lanfang, ZOU Jun, LIU Xiangnan. Assessment and analysis of the vulnerability of agricultural flood-waterlogging disas-ter—A study of Hengyang, Hunan. Resources and Environment in the Yangtze Basin, 2002, 11(3): 291-295. (in Chinese)
- 2. 汪朝辉, 王克林, 熊鹰, 等. 湖南省洪涝灾害脆弱性评估和减灾对策研究[J]. 长江流域资源与环境, 2003(6): 586-592. WANG Zhaohui, WANG Kelin, XIONG Ying, et al. Assessment of the vulnerability of flood-waterlogging disaster and coun-termeasures of disaster reductction in Hunan province. Resources and Environment in the Yangtze Basin, 2003(6): 586-592. (in Chinese)
- 3. 葛怡, 史培军, 刘婧, 等. 中国水灾社会脆弱性评估方法的改进与应用——以长沙地区为例[J]. 自然灾害学报, 2005, 14(6): 54-58. GE Yi, SHI Peijun, LIU Jing, et al. Improvement and application of vulnerability assessment methodology for flood hazards in China: Using Changsha Prefecture as a case study. Journal of Natural Disasters, 2005, 14(6): 54-58. (in Chinese)
- 4. 刘毅, 黄建毅, 马丽. 基于DEA模型的我国自然灾害区域脆弱性评价[J]. 地理研究, 2010, 29(7): 1153-1162. LIU Yi, HUANG Jianyi, MA Li. The assessment of regional vulnerability to natural disasters in China based on DEA model. Geographical Research, 2010, 29(7): 1153-1162. (in Chinese)
- 5. 何亚伯, 汪洋, 李袆琛, 等. 基于改进DEA交叉效率模型的洪水灾害区域性评价[J]. 中国安全生产科学技术, 2016, 12(5): 86-90. HE Yabo, WANG Yang, LI Yichen, et al. Evaluation on regional vulnerability of flood disaster based on improved DEA over-lapping efficiency model. Journal of Safety Science and Technology, 2016, 12(5): 86-90. (in Chinese)
- 6. 陈守煜. 可变模糊集合理论与可变模型集[J]. 数学的实践与认识, 2008, 38(18): 146-153. CHEN Shouyu. Theory of variable fuzzy sets and variable model sets. Mathematics in Practice and Theory, 2008, 38(18): 146-153. (in Chinese)
- 7. 王梅. 矿区生态脆弱性评价及土壤、植被特征分析——以六道沟流域为例[D]: [硕士学位论文]. 杨凌: 西北农林科技大学, 2012. WANG Mei. Evalauation on the eco-environmental vuluerability in the mining area and character analysis of the soil and veg-etation—A case syudy of Liudaogou watershed. Yangling: Northwest Agricultural and Forestry Science and Technology Uni-versity, 2012. (in Chinese)
- 8. 秦旭芝, 黎宁, 温中海, 等. 基于广西河池市胁迫风险的土壤环境脆弱性评价[J]. 中国环境监测, 2015(6): 71-76. QIN Xuzhi, LI Ning, WEN Zhonghai, et al. The evaluation of soil environmental vulnerability by the stress risks in Hechi City, Guangxi. Environmental Monitoring in China, 2015(6): 71-76. (in Chinese)
- 9. 樊运晓, 罗云, 陈庆寿. 区域承灾体脆弱性综合评价指标权重的确定[J]. 灾害学, 2001(1): 86-88. FAN Yunxiao, LUO Yun, CHEN Qingshou. Establishment of weight about vulnerability indexes of hazard bearing body. Journal of Catastrophology, 2001(1): 86-88. (in Chinese)
- 10. 张珍华. 基于可变模糊集理论的洛阳县域暴雨洪涝灾害脆弱性评价[D]: [硕士学位论文]. 开封: 河南大学, 2013. ZHANG Zhenhua. Vulneability assessment of storm flood disaters in Luoyang county based on variable fuzzy set theory. Henan: Henan University, 2013. (in Chinese)
- 11. 陈守煜, 胡吉敏. 可变模糊评价法及在水资源承载能力评价中的应用[J]. 水利学报, 2006, 37(3): 264-271. CHEN Shouyu, HU Jimin. Variable fuzzy assessment method and its application in assessing water resources carrying capacity. Journal of Hydraulic Engineering, 2006, 37(3): 264-271. (in Chinese)
- 12. 陈守煜. 工程模糊集理论与应用[M]. 北京: 国防工业出版社, 1998. CHEN Shouyu. Theory and application of engineering fuzzy sets. Beijing: National Defense Industry Press, 1998. (in Chinese)
