Modeling and Simulation
Vol.06 No.02(2017), Article ID:20579,8
pages
10.12677/MOS.2017.62011
Numerical Study of the Interaction Behavior of Two Non-Coplanar Cracks in Round Bars
Maigefeireti, Zeya Li
College of Science, Minzu University of China, Beijing

Received: Apr. 30th, 2017; accepted: May 19th, 2017; published: May 22nd, 2017

ABSTRACT
In the present study, the interaction of two non-coplanar cracks in round bars was investigated using the superposition finite element method (s-version FEM, S-FEM). The S-FEM, in the frame of finite element method, is a global-local overlaying method. The advantage of this method is saving the effort in FE modeling for multiple cracks. The virtual crack closure method is used to crack stress intensity factors. The interactions of two static cracks were analyzed by changing the relative distance between the cracks and the crack sizes. The analyses results may provide a reference for structure damage evaluation.
Keywords:Numerical Simulation, Superposition Fem, Fatigue Crack Growth, Two Cracks
圆棒表面非共面双裂纹交互影响数值分析
买歌菲热提,李泽亚
中央民族大学理学院,北京
收稿日期:2017年4月30日;录用日期:2017年5月19日;发布日期:2017年5月22日

摘 要
本文中,利用有限元重合网格法(s-version FEM, S-FEM)研究分析了圆棒表面两个非共面裂纹间的相互作用。有限元重合网格法是在有限元法的框架中,将整体网格与局部网格叠加的方法。该方法便于建立多个裂纹的有限元单元网格。利用虚拟裂纹闭合方法计算裂纹前端的应力强度因子。通过改变两个裂纹间的相对距离和裂纹尺寸等形状空间参数来分析其对应力强度因子的影响。此分析结果能对结构损伤评估具有一定的参考价值。
关键词 :数值模拟,有限元重合网格法,疲劳裂纹扩展,双裂纹

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
螺栓,锚栓和混凝土钢筋等,往往受到腐蚀疲劳的威胁。在腐蚀环境中,结构表面可观察到分布式裂纹群 [1] 。分布相近的缺陷易结合形成较大的裂纹,在腐蚀疲劳作用下扩展直到结构断裂失效。两共面裂缝在扩展过程中,会以临近端接触的方式结合 [2] ;两个非共面裂缝则不遵循直线裂纹扩展路径,而是呈现出互相避开的情况 [3] 。基于实验的结果,学者提出了评价两裂纹的疲劳寿命的近似方法。在ASME第XI部分和JSME Nal-2004都有提出近似评估的流程。在某些特定的情况下,两个裂缝可以重新定性为一个大型的虚拟裂纹,忽略两个非共面裂缝之间的垂直距离,该虚拟裂纹的深度是两个裂纹的平均深度或最大深度。因此,两裂纹的相对距离以及几何参数是影响两裂纹扩展的重要因素 [4] [5] 。
传统有限元方法在分析裂纹问题时,需要花大量的时间在裂纹单元的建模上。本文采用重合网格法。该方法是一种在有限元法的框架下,将整体与局部结合的方法。使用有限元重合网格法可以将裂纹看做从整体结构中独立出来的有限元模型,便于裂纹应力强度因子的计算和扩展模拟 [6] 。
2. 有限元重合网格法
为了提高计算精度,1993年J.Fish尝试在一个有限元网格上局部叠加一层细致的网格单元。这种网格叠加方法称为S-version FEM,即重合网格有限元法 [7] 。之后,J.Fish应用重合网格对多尺度问题进行了分析 [8] 。有限元重合网格法的优点是在大型结构中将有限的计算资源集中于研究于局部的影响,如孔、夹杂物或裂缝等。
以一个含有两个裂缝的有限体为例。利用重合网格法,问题域可由三个域来表示,如图1所示。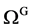 是无裂纹的整体区域。
是无裂纹的整体区域。 和
和 分别是含有裂纹的局部区域。这三个区域由三个独立的有限元单元模拟,利用统一坐标系统进行数值分析。
分别是含有裂纹的局部区域。这三个区域由三个独立的有限元单元模拟,利用统一坐标系统进行数值分析。

Figure 1. S-FEM model of a finite body with two cracks
图1. 含有两个裂纹的有限体的S-FEM模型图
当两个裂缝靠近彼此时,这两个局部模型可能会重叠。考虑到这种可能性,关于位移有如下假设:
 (1)
(1)
大写上标G,L1和L2分别表示整体场和两个局部场。为保持整体模型和局部模型之间的连续性,局部域模型在边界 和
和 上,位移边界条件应分别定义为
上,位移边界条件应分别定义为 和
和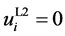 ,在上。将上述位移定义带入虚功原理,整理可得到如下矩阵形式:
,在上。将上述位移定义带入虚功原理,整理可得到如下矩阵形式:
 (2)
(2)
f是外力和体力之和。刚度矩阵是对称的, 。
。
在应用重合网格法计算之后,可以得到裂纹前端单元各节点的位移和反力。利用虚拟裂纹闭合方法 [9] 来进行计算分别可以计算出应力强度因子KI,KII,和KIII。
3. 计算模型以及应力强度因子计算验证
两个裂纹的相互作用影响通过交互因子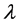 来表示,其表达式为:
来表示,其表达式为:
 (3)
(3)
 是两个裂纹中某一个裂纹的应力强度因子,代表与该裂纹尺寸位置相同的单一裂纹的应力强度因子。
是两个裂纹中某一个裂纹的应力强度因子,代表与该裂纹尺寸位置相同的单一裂纹的应力强度因子。
如图2(a)所示,受弯曲应力的圆棒表面含有两个表面裂纹。圆棒直径为D,裂纹深度为a,裂纹表面长度为s。如图3(a)所示,裂纹近似于一个半椭圆形与圆棒横截面相交,这个椭圆形半长轴为b。依据有限元重合网格法,我们分别建立了三个有限元单元网格,如图2(b)所示。采用了20节点六面体单元。通过局域网格,在裂纹前沿部分细化了网格,以提高计算精度。裂纹在横截面上的位置可以通过θ角度确定,该旋转角为横断面中心轴和裂纹的几何对称轴之间的夹角。裂尖上各点位置用α* = α/αw来表示,其中α是裂尖上某一点P与椭圆形短轴C点夹角,αw为裂尖A点与C点夹角(图3(b))。
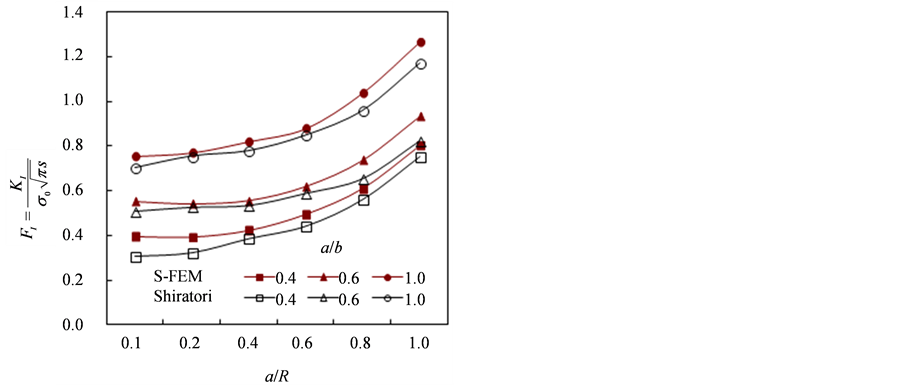
为了验证本文有限元重合网格法计算的精度,应用该方法与文献中记载的普通有限元法计算结果进行了对比。文献 [10] 中,受到弯曲应力作用的圆棒表面含有单一裂纹,裂纹深宽比分别选取a/b = 0.4,0.6和1.0。图4分别给出了裂纹最深处和裂纹外表面处的应力强度因子随裂纹深宽比的变化。将Shiratori的计算结果和重合网格法的计算结果进行对比,在裂纹最深处,两种方法计算结果基本一致;在表面处,最大误差也在合理范围内。
3.1. 相对距离
首先,我们分析了两个裂纹相对距离的变化对应力强度因子的影响。两个尺寸大小相同的裂纹,分别改变其水平距离和垂直距离。水平距离定义为两个裂纹临近端的圆周距离与裂纹的表面长度的比值,即S/s。垂直距离定义为轴向距离与裂纹深度的比值,即H/a。
 (a) (b)
(a) (b)
Figure 2. (a) Two non-coplanar cracks in a round bar under bending and (b) finite element models used in the analysis
图2. (a) 含有两个表面裂纹的受弯曲应力的圆棒,(b) 有限元单元网格
 (a) (b)
(a) (b)
Figure 3. Geometric parameters definitions for a crack in round bar
图3. 圆棒中裂纹的几何参数定义

 (a) (b)
(a) (b)
Figure 4. Comparison results of Stress intensity factor between S-FEM and general FEM (a) deepest point (b) surface point
图4. 重合网格有限元法和普通有限元的应力强度因子计算比较(a) 单一裂纹深部 (b) 单一裂纹表面
1) 只考虑水平距离时,两个裂纹在同一平面内,即H/a = 0 mm。我们考虑两种情况,第一种,两个裂纹关于圆棒的中心线对称分布,同时绕Z轴转动以改变水平间距S。第二种情况为,两个裂纹非对称分布,一个裂纹位置固定,另一个裂纹位置绕轴旋转从而改变S。第一种对称分布的情况(图5),当两个裂纹近端距离接近于0时,交互影响达到最大值,远端A和深点C的影响也存在但是表现较小。当距离变大时,在B点和C点的影响慢慢消失,反而在远端A出现了屏蔽效应,即交互因子出现了小于1.0的情况,裂纹2对裂纹1除了有交互增强的作用外,还存在交互减弱的影响。非对称情况下(图6),随着裂纹间距的扩大,交互增强的影响减弱并趋于常值。
2) 只考虑垂直距离时,我们计算了水平距离分别为S/s = 0.02 (图7)和S/s = 0.2 (图8)的对称分布情况。在文献 [11] 分析中指出,当H/a小于0.8时平板中的两个裂纹交互效果显著。在本研究中,我们也得到了类似的规律,如图所示临近端裂尖的增强交互效应在0 < H/a < 0.8范围内十分显著。
3.2. 裂纹尺寸
我们分析了裂纹尺寸对K值的影响。裂纹1作为目标裂纹,尺寸固定不变,并且两个裂纹的水平距离定为S/s = 1.2。裂纹2的深宽比a/s固定,同时改变裂纹尺寸a和s。图9给出了裂纹1的裂纹前端交互因子变化值。从整体来看,我们可以分析出大裂纹对小裂纹存在明显的交互增强效应,但在裂纹远端可以发现有交互减弱的趋势。为此,我们进行了进一步分析,裂纹2的表面长度s不变,改变裂纹深度,使其分别为a2 = 1.33a1和a2 = 0.67a1,得到了图10中最高和最低的交互因子分布曲线。之后,保持裂纹2深度不变,只改变裂纹的表面长度s,使其分别为1.5s1和0.5s1,此时的交互因子分布曲线最靠近当两个裂纹尺寸大小相同时的交互因子分布曲线(图10)。因此,我们可以发现:在两个裂纹间距一定的情况下,改变一个裂纹的表面长度,对另一个裂纹的应力强度因子的分布影响有限,裂纹的深度是两个裂纹相互影响的主要参数。但是,在图中也观察到了交互减弱的现象,当s2 = 1.5s1时,裂纹1的远端交互因子λ < 1.0。这种交互减弱的原因,我们分析认为是表面很长的裂纹改变了圆棒的应力分布情况,裂纹2开口很大时,在裂纹1远端一侧形成了压应力。

Figure 5. Interaction factor as a function of relative horizontal distance (H/a = 0)
图5. 交互因子随裂纹水平距离变化(对称分布H/a = 0)

Figure 6. Interaction factor as a function of relative horizontal distance (asymmetric distribution, H/a = 0)
图6. 交互因子随裂纹水平距离变化(非对称分布H/a = 0)
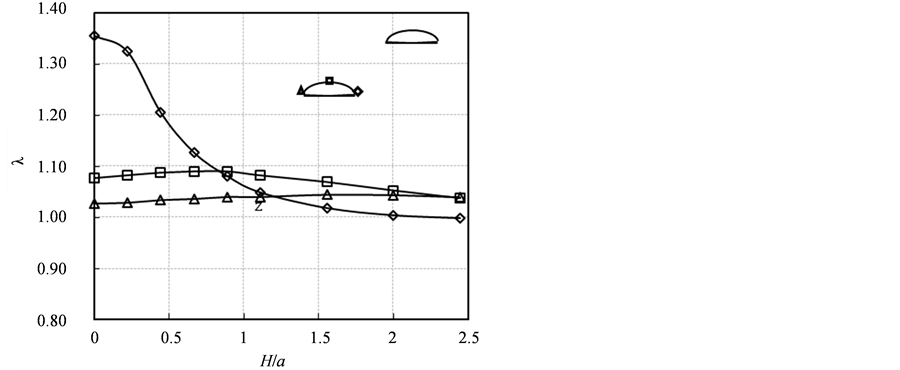
Figure 7. Interaction factor as a function of the relative vertical distance (S/s = 0.02)
图7. 交互因子随裂纹垂直距离变化(S/s = 0.02)

Figure 8. Interaction factor as a function of the relative vertical distance (S/s = 0.2)
图8. 交互因子随裂纹垂直距离变化(S/s = 0.2)

Figure 9. Variation of interaction factor of Crack 1 with the change in the crack size of Crack 2 (a/s is fixed)
图9. 裂纹1的交互因子随裂纹2尺寸变化而变化 (a/s固定)

Figure 10. Variation of interaction factor of Crack 1 with the change in the crack size of Crack 2 (a is fixed)
图10. 裂纹1的交互因子随裂纹2尺寸变化而变化(a固定)
4. 结论
本文通过有限元重合网格法对圆棒表面两个非共面的裂纹进行了数值分析。通过参数分析得到相互影响因子与两裂纹的尺寸以及相对距离的关系。相对距离和裂纹尺寸被认为是影响相互作用强度的两个主要因素。两共面裂纹在圆周距离小于表面长度60%的情况下相互影响的作用效果显著,可近似为一个大裂纹。增加垂直距离可能会削弱这种相互作用,两个裂纹需独立进行分析。此外,裂纹深度在相互作用中产生着主要作用,而裂缝表面长度主要影响裂尖远端。
文章引用
买歌菲热提,李泽亚. 圆棒表面非共面双裂纹交互影响数值分析
Numerical Study of the Interaction Behavior of Two Non-Coplanar Cracks in Round Bars[J]. 建模与仿真, 2017, 06(02): 90-97. http://dx.doi.org/10.12677/MOS.2017.62011
参考文献 (References)
- 1. Kitagawa, H., Fujita, T. and Miyazawa, K. (1978) Small Randomly Distributed Cracks in Corrosion Fatigue. ASTM Internation-al.
- 2. O’Day, M.P. and Curtin, W.A. (2004) A Superposition Framework for Discrete Dislocation Plasticity. Journal of Applied Mechanics, 71, 805-815. https://doi.org/10.1115/1.1794167
- 3. Iida, K., Ando, K. and Hirata, T. (1984) An Evaluation Technique for Fatigue Life of Multiple Surface Cracks. Naval Architecture and Ocean Engineering, 22, 177-199.
- 4. Kamaya, M. (2003) A Crack Growth Evaluation Method for Interacting Multiple Cracks. JSME International Journal. Series A, Solid Mechanics and Material Engineering, 46, 15-23. https://doi.org/10.1299/jsmea.46.15
- 5. 谢伟, 张炯, 黄其青, 等. 有限大体复合型表面裂纹断裂特性研究[J]. 机械科学与技术, 2012, 31(3): 363-366.
- 6. 买歌菲热提, 菊池正纪, 买买提明艾尼, 等. 基于有限元重合网格法的三维疲劳裂纹扩展模拟与验证[C]//北京力学会. 北京力学会第18届学术年会论文集, 2012.
- 7. Fish, J. and Markolefas, S. (1993) Adaptive s-Method for Linear Elastostatics. Computer Methods in Applied Mechanics and Engineering, 104, 363-396. https://doi.org/10.1016/0045-7825(93)90032-S
- 8. Fish, J. and Guttal, R. (1996) The s-Version of Finite Element Method for Laminated Composites. International Journal for Numerical Methods in Engineering, 39, 3641-3662. https://doi.org/10.1002/(SICI)1097-0207(19961115)39:21<3641::AID-NME17>3.0.CO;2-P
- 9. Krueger, R. (2004) Virtual Crack Closure Technique: History, Approach, and Applications. Applied Mechanics Reviews, 57, 109-143. https://doi.org/10.1115/1.1595677
- 10. Shiratori, M., Miyoshi, T. and Zhang, G.R. (1986) Analysis of Stress Intensity Factors for Surface Cracks Subjected to Arbitrarily Distributed Surface Stresses (3rd Report). Transactions of the Japan Society of Mechanical Engineers, 660-662. (In Japanese)
- 11. Kamaya, M. (2008) Growth Evaluation of Multiple Interacting Surface Cracks. Part II: Growth Evaluation of Parallel Cracks. Engineering Fracture Mechanics, 75, 1350-1366. https://doi.org/10.1016/j.engfracmech.2007.07.014