电梯运行方案的计算机模拟优化设计 Computer Simulation and Optimization Design of Elevator Operation Plan

doi:10.12677/MOS.2018.74025

Modeling and Simulation
Vol. 07 No. 04 ( 2018 ), Article ID: 27786 , 14 pages
10.12677/MOS.2018.74025

Computer Simulation and Optimization Design of Elevator Operation Plan

Maoyi Zhang

●How to Cite this Article

School of Information and Control Engineering, China University of Mining and Technology, Xuzhou Jiangsu

Received: Nov. 9^th, 2018; accepted: Nov. 21^st, 2018; published: Nov. 29^th, 2018

ABSTRACT

This paper solves the design problem of elevator dispatching scheme in hospital outpatient building by computer simulation. This paper analyzes the following three problems: the use of elevators, the transportation efficiency in rush hours, and the complex elevator dispatching problem. This topic combines MATLAB software, mainly using the computer simulation method. The characteristic of this paper is to simulate the running process of the elevator with greater randomness, which greatly reduces the difficulty of solving the problem. This paper not only evaluates the existing elevator operation scheme, but also gives a better design for the elevator operation management scheme in high-rise commercial building, and provides a theoretical basis for it.

Keywords:Elevator, Dispatching, MATLAB

电梯运行方案的计算机模拟优化设计

张茂仪

中国矿业大学信息与控制工程学院，江苏徐州

收稿日期：2018年11月9日；录用日期：2018年11月21日；发布日期：2018年11月29日

摘要

运用计算机模拟等模型解决了医院门诊大楼中的电梯调度方案的设计问题。针对以下的三个问题：电梯的使用、高峰时期的运载效率、复杂的电梯调度问题进行了分析。结合MATLAB软件，主要使用了计算机模拟的方法。该文的特点是对随机性较大的电梯运行的过程进行了模拟，大大降低了问题的求解难度。该文不仅评价了现有的电梯运行方案，还为高层商务楼中的电梯运行管理方案给出较优设计，并为其提供了理论依据。

关键词 :电梯，调度，MATLAB

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

医院门诊大楼中的电梯调度方案的设计问题，针对以下的三个问题：电梯的使用、高峰时期的运载效率、复杂的电梯调度问题进行了分析。

第一问题，对于电梯的使用，考虑节约能源和尽力满足客户需求两个角度，确定了以用户平均等待时间，以及停靠次数作为电梯运行调度方案的两个主要指标，并据此建立模糊综合评价模型。其中，结合乘客心里特征以及电梯能耗特点，给出了平均等待时间与停靠次数对于不满意度的具体隶属函数，并考虑医院以效率优先的原则，确定了平均等待时间以及停靠次数两种不满意度的线性重要权重为0.8与0.2 [1]。

第二问题，电梯评价主要参考其高峰时期的运载效率。通过对医院高峰时期的人流分析，假设高分期分流服从 $N (3600, 1200)$ 的正态分布，以及每个人去往医院的任意的楼层数服从1~29的离散均匀分布。进一步，设计了以计算机仿真进行统计计算每个候选方案平均等待时间和平均停靠次数的整理思路框架，对任意候选方案采取100轮次的高峰人流电梯调度仿真。对具体每一轮高峰人流电梯调度仿真，进一步建立了电梯运行流程模型。最终，使用MATLAB实现了单次高峰人流调度计算以及整体仿真估计流程，并针对电梯停靠的常用的单双层和高低层一共7种方案，进行了100次的仿真计算并获得了每个候选方案的平均等待时间和停靠次数，具体结果详见下文6.3.3。将所得结果代入问题一的模糊综合评价模型中，最终获得不满意度最小的最优调度方案为高低层电梯分配调度方案，其中A、C电梯停靠范围4~17与B、D电梯停靠范围18~29，其不满意度值最小位为0.1503。

第三问题，要求结合实际情况，进一步对我们对问题二中的方案作出调整，用于解决更为复杂的电梯调度问题。故考虑在第二问的基础上，进一步考虑来自地下车库的乘客需求，将第二题的候选拿方案包含兼顾对于地下停靠点的选择。沿用第二问在整体计算流程思路上，但是具体每轮的高峰人流由地下车库的需求以随机0.08概率产生，并计算考虑每轮电梯作业新增的对运行时间以及每位乘客等待时间的延迟。最后，针对电梯停靠高低层一共7种方案，进行了100次的仿真计算并获得了每个候选方案的平均等待时间和停靠次数，具体结果详见下文6.4.2。将所得结果代入问题一的模糊综合评价模型中，最终获得不满意度最小的最优调度方案为高低层电梯分配调度方案，其A、C电梯停靠范围−1，−2，4~16与B、D电梯停靠范围−1，−2，17~29，其不满意度值最小为0.1506。

2. 电梯调度问题提出

作为医院的垂直交通工具，人们对电梯的需求变得越来越复杂。在每天就医人数高峰期，医院电梯是非常拥挤的，医院在要求减少电梯设备占用建筑物的核心空间的同时，希望电梯交通系统的服务数量和质量有大幅度提高。因此，如何对现有资源合理利用，缓解电梯的运输压力，缩短病人和医生的等待时间，是医院所必须解决的问题，也是电梯垂直交通系统面临的新的挑战。

徐州市中心医院拟在铜山区新建一个31层的门诊大楼，其中含有地下二层(地下二层为停车场，地下一层为药品及医疗器械运送场所)。门诊大楼内部设有四部电梯，编号分别为A梯、B梯、C梯、D梯，其中A梯、B梯为无担架病人及家属专用电梯，每个电梯最多载重1350千克；C梯、D梯为有担架病人及医生专用电梯，每个载重1000千克。每个电梯内部有33个按钮，其中包括开门按钮、关门按钮和楼层按钮，编号为−2，−1，1，2，3，4…，29。电梯外部含有两个按钮，即向上运行按钮和向下运行按钮。建筑顶层与地下二层例外，建筑顶层只设置有向下运行按钮，地下二层只设置有向上运行按钮。电梯开关门完成时间设定为1秒。电梯到达每层后上下人的时间设定为8秒。电梯从静止开始运行到下一层的时间设置为2秒，而运行中通过一层的时间为1秒。在凌晨2:00~4:30之间，如若没有请求信号，A梯、B梯自动停在16层，C梯、D梯自动停在6层。当电梯下到−2，−1层后，如果没有请求信号，电梯自动回到1层。徐州市中心医院的门诊大楼一楼平面图见下见图1：

Figure 1. Floor plan of the outpatient building of Xuzhou Central Hospital

图1. 徐州市中心医院的门诊大楼一楼平面图

请针对徐州市中心医院就医人数高峰期的情况(高峰期需要使用电梯500~1000人次)，对电梯调度问题建立数学模型，以期获得合理的优化方案。

问题1：给出若干合理的模型评价指标；

问题2：针对徐州市中心医院门诊大楼情况给出一个合理的调度方案；

问题3：在第二问的基础上，将数学模型进一步实际化，提出合理化的建议和措施，用于解决更为复杂的电梯调度问题。

3. 模型假设

假设1：所有乘客乘坐电梯时均遵循先到先乘坐的规则；

假设2：普通病人与医生也乘坐C梯、D梯，只是出现有担架病人及医生时，优先让有担架病人及医生乘坐，为简化问题，通常认为有担架病人及医生占总体比重较小，所以由这部分产生的等待时间不计；

假设3：假设人均体重为65 kg，即A梯、B梯最大承载20人，C梯、D梯最大承载15人；

假设4：在高峰期，医护员工上班，以及病人就医来到医院的时间整体服从正态分布 $N (μ, σ^{2})$ ；

假设5：三层及以下楼层的员工上下楼忙时走楼梯，闲时乘电梯；四层及以上楼层的员工上下楼均乘电梯，不走电梯；

假设6：客运电梯在7~9时上班高峰时上行运行停靠，下行时不在途中停靠；

假设7：电梯使用者到达电梯时，通常不会等待未到达达的其他乘客过长时间，所以设电梯的整体满载率为50%；

假设8：问题2中不考虑地下车库。

4. 符号说明

$T_{w}$ ：人均等电梯时间；

${\bar{T}}_{w}$ ：大规模仿真的平均人均等电梯时间；

$N$ ：停靠次数；

$\bar{N}$ ：大规模仿真的平均停靠次数；

$f_{W} (T_{w})$ ：人均等待电梯时间不满意度隶属值；

$f_{N} (N)$ ：平均停靠次数不满意度隶属值；

$μ$ ：电梯承载率；

$T_{E n d}$ ：该电梯当前批次的最终出发时间，也就是当前批次最后一个人的到达时间；

$L_{E n d}$ ：该电梯当前批次的最大出发楼层，也就是电梯需要运行的最高位置，到达后即返回。

5. 概念引入及问题分析

5.1. 概念的引入

分层次运行方式：每部电梯负责一定的楼层，只在其负责的楼层和底层停靠，例如规定电梯负责的楼层是11~15层，则该电梯只能停留于11~15层。单双层运行方式：电梯只在单层或双层停靠，例如电梯为单层运行，则该电梯只能在单层(1、3、5…层)停靠。电梯直达某高层以上运行方式：电梯只能在规定的楼层及其以上的任意楼层停靠，而不能在规定以下的楼层停靠，是分层次运行的一种方式。

5.2. 问题分析

对于问题1，要求我们给出若干合理的模型评价指标，对于电梯的使用，可以考虑节约能源和尽力满足客户需求两个角度来具给出电梯运行方案的评价指标。问题2要求针对徐州市中心医院门诊大楼情况给出一个合理的调度方案，可以考虑我们在常用的电梯运行方案中例如单双层停靠与高地层停靠等方式中选择合适的方式，根据问题的评价指标对其进行评价选择。问题3要求在第2问的基础上，将数学模型进一步实际化，可以进一步考虑电梯运行细节，楼层使用，在更为复杂的电梯调度过程中问题，根据问题一的指标对相应的方案进行选择。

6. 模型的建立与求解

6.1. 模型准备与分析

6.1.1. 电梯停靠方案

高楼建筑常用的电梯停靠方式主要有两种，分别为单双层与高低层停靠方式，在本文的医院高楼设定中，ABCD四部电梯，可以采用如下表1所示的电梯停靠方式。

Table 1. Each elevator parking mode

表1. 每台电梯停靠方式

由于在医院中，C梯、D梯为有担架病人及医生专用电梯，所以必须满足这两梯覆盖所有楼层的停靠点。同时，剩余电梯为了满足其他乘客的电梯使用也应满足覆盖所有楼层的停靠点。进一步，根据各类电梯的数量，表1展示了最为合理的单双层和高低层电梯调度分配方式。

6.1.2. 高峰时刻

对电梯调度方案的优劣，主要在于其高峰时刻调度性能的优劣，为此我们对医院高峰时期人员乘坐电梯的过程进行模拟。我们设定人员到达的时间分布为正态分布 $N (μ, σ^{2})$ ，员工到达后，三层及以下楼层的员工走楼梯，四层及以上楼层的员工乘电梯，所有人乘坐电梯时均遵循先到先乘坐的规则。我们结合员实际电梯使用高峰时间分布情况经过试模拟后认为二者的较优取值为： $μ = 3600$ ， $σ = 1200$ 。

由员电梯使用高峰时段人员到达的时间分布(见图2(a)，其中横轴为时间(单位：秒)，纵轴为人数)可知，该高峰时间为持续两个小时，该过程发生在7点至9点之间，此时段内医护人员上班以及早晨就医人员大量进入，造成该时段内的电梯使用的高峰。

(a) (b)

Figure 2. Data distribution: (a) Arrival time distribution map; (b) Map of arrival levels

图2. 到达数据分布：(a) 到达时刻分布图；(b) 到达层数分布图

对于到达人数，根据题意，高峰期需要使用电梯500~1000在本问题中，我们设置高峰使用人数为该区段的中点750人，并且所有人员从1层前往1~29层的数量程均匀分布，上图2(b)给出了所有750人在某次高峰时段达到不同医院楼层的人数分布。从上图可以看出，各层停靠需求相对均匀，而实际中若有相关停靠位置分布数据可依据实际分布模拟，此处由于缺少数据，就用均分分布代替。

6.1.3. 电梯运行过程

由于关于电梯的问题类似，所以为了找到比较通用的解决办法，我们决定设计算法以便于对人乘坐电梯的过程进行模拟，得出必要的数据，最后对电梯的运行方式进行评价。高峰期间内，人员的到来服从对时间的正态分布，人工到来之后在停靠自己所在楼层的电梯前排队，其中不包括1、2、3层的员工。在电梯运行一周的过程中，不断的向需要停放人员的楼层停靠直到最高层，电梯运行一周的步骤过程如下：

Step 1：电梯开门，排在前面的一定数量人依次进入电梯，电梯门关闭，向上行驶；

Step 2：判断第i层是否有人下。若无，则不在第i层停靠，电梯驶向第i + 1层。若有，则电梯在第i层停靠，开门，要出人员依次走出电梯，关门。令i = i + 1，判断电梯是否达到最高期望楼层，若否向Step 2开头，若是则转向Step 3；

Step 3：电梯停靠在最高期望楼层，电梯中人员已全部下完，驶向靠在一层。

6.1.4. 方案设计思路

在电梯的调度方案设计中，我们需要在第一问中确定，电梯调度方案的评价指标，并依据评价指标建立起电梯方案的模糊评价模型。在第二和第三问中，我们采用编程实现各种备选方案的调度算法，结合医院电梯和高峰人流实际数据，对每种备选方案仿真100次，获得人均等待时间 $T_{w}$ 和停靠次数的平均值 $N$ ，并代入第一问中确立的模糊评价模型对每个候选方案进行评价，评价结果最优的方案即为我们所选择的医院电梯调度方案。具体的思路流程可以归纳为如下图3的思路流程图。

Figure 3. Design flow chart of elevator dispatching plan

图3. 电梯的调度方案设计思路流程图

6.2. 问题1——电梯调度方案评价指标

6.2.1. 评价指标

关于电梯评价的两个方面，我们节约能源和尽力满足客户需求两方面出发去寻找。在尽力满足用户需求方面，尤其是在医院这种服务机构内，可以认为是首要需满足的重要指标。对于每个电梯用户而言，尽可能少的等待时间可以被作为最主要的考查标准 [2]。

另一方面，在尽可能缩短用户等待方案时间的调度方案下，应该尽可能减少电梯的能耗，在电梯的使用中，如果越是集中目标楼区的人群在一次承运作业中，减少频繁多点的停靠，能够有效的起到节约能源的作用。

综合上述分析，本文选取如下两个指标作为电梯调度方案的评价指标。

$评价指标 {\begin{matrix} \begin{array}{l} 满足乘客需求： \\ 节约能源： \end{array} & \begin{array}{l} 平均等待时间 \\ 停靠次数 \end{array} \end{matrix}$

6.2.2. 电梯调度方案模糊综合评价方法

1) 平均等待指标的隶属化

我们首先处理等待时间。我们定义等待时间取下列值时，不满意度也如下表2变化：

Table 2. Dissatisfaction with waiting time

表2. 关于等待时间的不满意度刻画

注：当等待时间大于1000 s时，可认为员工已经“麻木”，因此态度也是很不满意。

由于人等待的心理时间与现实时间成二次函数，所以为了连续量化指标，我们采取二次函数和对数函数最为隶属函数：

$f (x) = {\begin{cases} a {(x + b)}^{2}, 1 \leq x \leq 3 \\ c \ln x + d, 3 \leq x \leq 5 \end{cases}$

其中 a,b,c,d 为待定常数，且有：

a) 当很满意时，隶属度为0，即 $f_{W} (200) = 0$ ；

b) 当较满意时，隶属度为0.8，即；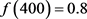

c) 当很不满意时，隶属度为1，即 $f (1000) = 1$ 。

由于在上述定义中，自变量与因变量的数量级之比有1000倍之多，拟合出来的参数数量级一定很小，这往往会造成最终拟合出来的参数会不精确。为了使各类待定常数更加精确，我们让等待时间的数值缩

小200倍，这样减小了它们之间的数量级差距。即 $x^{'} = \frac{x}{200}$ 。因此，上述隶属函数的定义可以更改为： $f (1) = 0$ ， $f (3) = 0.8$ ， $f (5) = 1$ 。

最终求得 $a = 0.2, b = - 1, c = 0.3915, d = 0.3699$ 。则

该隶属函数的图像如图4：

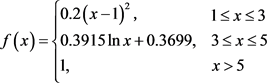
Figure 4. Membership function of per capita waiting time

图4. 人均等待时间的隶属函数

2) 停靠次数指标的隶属化

关于节约能源方面，由于能源只和停靠次数有关，而和人的心理等因素无关，故可将一次函数作为停靠次数的隶属函数。简单起见，我们将以上三个指标数值大小做一定的处理，使其间隔相同，这样就能取同一个隶属函数。于是，定义如表3。

设隶属函数为： $f (x) = a x + b, 0 \leq x \leq 725$ ，其中， $a, b$ 为待定常数，且有：

a) 当很满意时，隶属度为0，即f (125) = 0 ；

b) 当很不满意时，隶属度为1，即 $f (725) = 1$ 。

Table 3. Depiction of the dissatisfaction of the number of stops

表3. 关于停靠次数的不满意度刻画

同理我们让等待时间的数值缩小125倍，这样减小了它们之间的数量级差距。即 $x^{'} = \frac{x}{125}$ 。因此，上述隶属函数的定义可以更改为： $f (1) = 0$ ， $f (5) = 1$ 。求得 $a = 0.25, b = - 0.25$ 。则

$f (x) = {\begin{matrix} \begin{array}{l} 0.25 x - 0.25, \\ 1, \end{array} & \begin{array}{l} 1 \leq x \leq 5 \\ x > 5 \end{array} \end{matrix}$

该隶属函数图像如下图5：

Figure 5. Energy saving membership function

图5. 节约能源方面的隶属函数

3) 线性加权评价模型

在前面的分析中，我们讨论了人的平均等待时间和停靠次数这两个指标的意义。在对医院电梯调度方案的评价模型中，认为客户需求是相对于节约能源更为重要的，故二设前者的系数为0.8而后者的系数为0.2。

综上分析，该线性加权评价模型可以如下建立，令：

$f = 0.8 \times f_{W} (T_{w}) + 0.2 \times f_{N} (N)$

其中，各项指标如下确定：

${\begin{cases} T_{w} ， N_{3} 分别由计算机模拟数据整理得到 \\ f_{W} (T_{w}) = {\begin{matrix} \begin{array}{l} 0.2 {(\frac{T_{w}}{200} - 1)}^{2}, \\ 0.3915 \ln \frac{T_{w}}{200} + 0.3699, \\ 1, \end{array} & \begin{array}{l} 200 \leq x \leq 600 \\ 600 \leq x \leq 1000 \\ x > 1000 \end{array} \end{matrix} \\ f_{N} (N) = {\begin{matrix} \begin{array}{l} 0.25 \frac{N}{125} - 0.25, \\ 1, \end{array} & \begin{array}{l} 125 \leq T_{a} \leq 750 \\ T_{a} > 750 \end{array} \end{matrix} \end{cases}$

6.3. 问题2——电梯调度方案设计

6.3.1. 仿真统计思想

计算机模拟的主要过程是通过计算机随机产生等待人群的信息(包括到达时间、目的楼层等)，并通过这些信息来控制电梯的运行，从而更准确地确定电梯运行中的各项指标。

在电梯运行的模型中，有很多具有随机因素的变量，例如：排队人员要到达的楼层数，电梯每一次运行的停靠楼层等。除此之外，每个人的等待时间以及电梯的运行时间都具有不确定因素。因此，为了更准确地评价电梯的两种运行方式，我们将采用模拟的方法对电梯的各种备选方案进行模拟运行，并导出个方案的评价指标诸如平均等待时间与停靠次数 N [3]。

由于每个候选方案的每次模拟不可避免均有误差，为使误差最小化，我们每个方案模拟100次，然后对100次仿真结果的平均等待时间与停靠次数求平均值，即

$\bar{N} = \frac{\sum_{i = 1}^{100} N^{i}}{100}, {\bar{T}}_{w} = \frac{\sum_{i = 1}^{100} T_{w}^{i}}{100}$

其中， $T_{w}^{i}$ ，分别为某调度方案第i次仿真的平均等待时间与停靠次数。整体的仿真思路流程可以归纳为如下图6。

Figure 6. Overall flow chart of simulation and statistical calculation of average waiting time and stopping number

图6. 平均等待时间与停靠次数仿真统计计算整体流程图

6.3.2. 高峰时期电梯运行流程模型

6.3.1中我们已经给出平均等待时间 ${\bar{T}}_{w}$ 与停靠次数 $\bar{N}$ 仿真统计计算整体流程图，但对每一个仿真方案的具体每一次仿真的停靠次数 $N^{i}$ 与平均等待时间 $T_{w}^{i}$ 还未给出具体细节的讨论。

在医院的电梯调度中，我们有具体4架电梯，在我们的备选方案中，根据6.1的分析，由于医院中C，D电梯由于担架病人与医生优先专用的必须覆盖全部停靠点，同时我们设定了而其余电梯为了更好的服务一般病人也必须覆盖全部的停靠点，所有以A、B电梯也必须覆盖全部的停靠点。所以在设计备选方案时，可以将AC的覆盖方式设置成一样，BD设置成一样，另外，对于高低层调度方案，尽量考虑电梯负责楼层的均衡，所以以14~19层作为分界点，设计了7调度种方案，连同单双层停靠方案一起列出如下表4。

Table 4. Elevator stop candidate scheme

表4. 电梯停靠候选方案

对于某个承载方案的具体，在实际运行中，往往不可能总是满载，根据时间的设定，乘客不会等待还没到达电梯的客户太长时间，为简化过程其见，我们设定任意一架电梯，当，当电梯的承载率到达 $μ$ 时就出发。

对于某个候选方案的某一次仿真，其停靠次数 $N^{i}$ 与平均等待时间 $T_{w}^{i}$ 计算过程可以罗列如下列步骤：

Step 1：初始化得到本轮高峰所有750个人的到达时刻，以及每个人的期望到达楼层列表，并按照到达时间T的以及期望到达楼层L，按照到达时间的前后排序，早到在前晚到在后，并设定ABCD电梯的当前可用时间为 $T a, T b, T c, T d = 0$ ；

Step 2：对时间为前i位的电梯乘客，的期望到达楼层Li进行判断其属于AC电梯还是BD电梯，所属于AC电梯进入Step 3，若属于BD电梯则进入Step 4；

Step 3：若AC电梯的当前可用时间 $T a \leq T c$ ，则当前第当i位电梯乘客进入A电梯，此时若A电梯达到承载率 20×μ 人则A电梯出发，更新A电梯的当前可用时间Ta，并计录A电梯此次的停靠次数Na；若 $T a > T d$ ，则当前第当i位电梯乘客进入C电梯，此时若C电梯达到承载率 15×μ 人则C电梯出发，更新C电梯的当前可用时间Tc；并计录C电梯此次的停靠次数Nc；

Step 4：若BD电梯的当前可用时间 $T b \leq T d$ ，则当前第当i位电梯乘客进入B电梯，此时若B电梯达到承载率 $20 \times μ$ 人则B电梯出发，更新B电梯的当前可用时间Tb，并计录B电梯此次的停靠次数Nb；若 $T b > T d$ ，则当前第当i位电梯乘客进入D电梯，此时若D电梯达到承载率 $15 \times μ$ 人则D电梯出发，更新D电梯的当前可用时间Td，并计录D电梯此次的停靠次数Nd；

Step 5：若 $i = i + 1$ ，若 $i \leq 750$ 返回Step 2；

Step 6：根据Step 2~4过程，对A，B，C，D的所有批次运输电梯的每一个人的等待时间，和每次电梯出发的停靠的次数，统计算出第i伦高峰期间电梯停靠次数与平均等待时间 $T_{w}^{i}$ 。

在上述的过程，电梯ABCD电梯到达规定运载量后，其可用更新的规则计算方法如下；

$T x = T_{E n d} + (L_{E n d} - 1) \times 2 + N \times (8 + 2) + (N + 1)$

其中 $x \in {a, b, c, d}$ ，上式中各项的意义如下

$T_{E n d}$ ：该电梯当前批次的最终出发时间，也就是当前批次最后一个人的到达时间；

$L_{E n d}$ ：该电梯当前批次的最大出发楼层，也就是电梯需要运行的最高位置，到达后即返回；

$N$ ：该电梯当前批次的停靠次数。

6.3.3. 模型求解结果

采用MATLAB编程实现6.3.2中的电梯运行流程模型计算每次模拟人流高峰中电梯人均等待时间与停靠次数，并依据6.3.1的仿真框架重复该过程100次最后计算得到平均等待时间 ${\bar{T}}_{w}$ ，平均停靠次数 $\bar{N}$ ，在该仿真中设定承载率到达 $μ = 50 %$ ，总人次750，到达时间服从 $N (3600, 1200)$ 的正态分布，个人期望到达楼层服从1~29的离散均匀分布，最终仿真结果，以及代入问题1的模糊综合评价模型的方案得分结果如下表5。

Table 5. Simulation results of candidate solutions

表5. 候选方案仿真结果

根据不满意度最小原则，方案5高低，A、C电梯停靠范围4~17与B、D电梯停靠范围18~29，其不满意度值最小位，最优方案。下图7给出了当前方案下，100次仿真里所有人的等待时间–人数分布图。

Figure 7. Waiting time-population distribution map

图7. 等待时间–人数分布图

从上面的分布图可以看出，绝大多数的人的等待时间在4分钟以内。

6.4. 问题3——电梯调度方案设计(含地下停车库)

6.4.1. 电梯运行流程模型(含地下停车库)

在问题3中，我们考虑含地下停车库情况的，我们重新选择我们的备选方案，如下表6所示。

Table 6. Elevator stop candidate scheme

表6. 电梯停靠候选方案

在新的备选方案中，我们排除了低效的单双层方案，而都用高低层方案进行候选，进而根据计算机模拟仿真的结果寻找高低层方案中最优的电梯停靠分界点。由于从地下车库停车进入医院的乘客，可能去往高层也去可能去往低层。所以，所有方案要兼顾地下一二层的乘客。

对于问题3的电梯运行仿真模拟，其大体思路和问题2中的一样，但对于，电梯ABCD电梯到达规定运载量后，其可用更新的规则计算方法修改；

$T x = T_{E n d} + (L_{E n d} - 1) \times 2 + N \times (8 + 2) + (N + 1) + F_d e l a y$ ，其中 $x \in {a, b, c, d}$ ，上式中各项的意义如下

$T_{E n d}$ ：该电梯当前批次的最终出发时间，也就是当前批次最后一个人的到达时间；

$L_{E n d}$ ：该电梯当前批次的最大出发楼层，也就是电梯需要运行的最高位置，到达后即返回；

$N$ ：该电梯当前批次的停靠次数。

与问题二中不同的是， $F_d e l a y$ 是由于该批次中含有车库到达的人员，电梯从地下层接下面的乘客造成的延迟，在本文中，为简化计算流程，以如下方式计算

上式表示以百分之8的概率对某次电梯乘客，该数据以徐州市当地司机车保有量以及医院用车频率的网上数据估计。同样，若该批次的乘客也按照顺序是否在需要更新相应的个人等待时间。

6.4.2. 模拟计算结果

根据不满意度最小原则，方案3最优，A、C电梯停靠范围4~16与B、D电梯停靠范围17~29，其不满意度值最小位，为最优方案。下图8给出了当前方案下，100次仿真里所有人的等待时间–人数分布图。

Table 7. Simulation results of candidate solutions

表7. 候选方案仿真结果

Figure 8. Waiting time-population distribution map (South Korean elevator)

图8. 等待时间–人数分布图(韩电梯)

从上面的分布图可以看出，绝大多数的人的等待时间在5分钟以内，在加入了底层电梯的影响后，时间等待分布趋势与没有电梯时产生了明显的差异，整体等待时间也增长了。

7. 模型的评价与改进

7.1. 模型的评价

1) 全文的模型求解都运用了计算机模拟，使求解更接近现实，方案的评价及确定更加简单和合理；

2) 在问题二中，采用计算机仿真方法，实现对候选方案的重要指标的估计，缩小了模型的范围，而且在列举出的较优方案中直接对其模拟，易于求得最优方案；

3) 在问题三中，利用前面的结果加以适当调整，通过模拟得出最优方案，简单易行。

7.2. 模型的改进

1) 由于模型比较理想化，和现实中差距较大，我们的模型还存在不足之处。若要模型更加接近现实，更加精确，则必须重新考虑，放弃一些理想化的假设；

2) 在求解问题二和问题三的运行方案时，要使结果更加精准，必需建立统一的优化模型，或者将所有可列结果进行模拟，而不是在所给出的有限的几种方案中模拟，从中选取最优解。

8. 结束语

本文结合MATLAB软件，使用了计算机模拟的方法，对随机性较大的电梯运行的过程进行了模拟，大大降低了问题的求解难度。本文不仅评价了现有的电梯运行方案，还为高层商务楼中的电梯运行管理方案给出较优设计并提供了理论依据。

文章引用

张茂仪. 电梯运行方案的计算机模拟优化设计
Computer Simulation and Optimization Design of Elevator Operation Plan[J]. 建模与仿真, 2018, 07(04): 209-222. https://doi.org/10.12677/MOS.2018.74025

参考文献

1. 韩中庚. 数学建模方法及其应用[M]. 第二版. 北京: 高等教育出版社, 2009.

2. 张海龙, 高东红. 几种电梯运行模式的比较及应用[J]. 数学的实践与认识, 2008(10): 65-69.

3. 李庆民, 刘君, 张志华, 武器系统仿真模型的可信性验证方法研究[J]. 系统仿真学报, 2006(12).

期刊菜单