Statistics and Application
Vol.07 No.02(2018), Article ID:24337,6
pages
10.12677/SA.2018.72014
Sieve Bootstrap Test for Changes between Unit Root Process and Fractional Integrated Processes
Mingcan He, Guolong Fu
School of Mathematics and Statistics, Qinghai Normal University, Xining Qinghai
Received: Mar. 15th, 2018; accepted: Apr. 2nd, 2018; published: Apr. 9th, 2018

ABSTRACT
This paper aimed to test change point from unit root process to fractional integrated process as well as fractional integrated process to unit process via a Dickey-Full ratio statistic. A Sieve Bootstrap method was proposed to determine the critical values. Simulations indicate that our proposed method can control the empirical size well both under the unit root and fractional integrated process null hypotheses, and gives satisfy empirical powers under two alternative hypotheses if the change point location does not too back. Furthermore, Dickey-Full ratio statistic has better performance when detecting those changes which from unit root process to fractional integrated process.
Keywords:Unit Root Process, Fractional Integrated Process, Changes Point, Sieve Bootstrap
单位根过程与分整过程间变化变点的Sieve Bootstrap检验
何明灿,付国龙
青海师范大学数学与统计学院,青海 西宁
收稿日期:2018年3月15日;录用日期:2018年4月2日;发布日期:2018年4月9日

摘 要
本文基于Dickey-Full比率统计量研究了从单位根过程向分整过程变化变点,以及从分整过程向单位根过程变化变点的检验问题,并提出了用于确定检验统计量临界值的Sieve Bootstrap方法,数值模拟结果表明本文方法在单位根及分整过程原假设下都能很好的控制检验水平,在变点位置不是太靠后时,对两种备择假设下的变点都有较高的检验势,且在检验从单位根过程向分整过程变化变点时效果更显著。
关键词 :单位根过程,分整过程,变点,Sieve Bootstrap

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
过去三十年里,有越来越多的证据表明许多时间序列数据中存在从平稳向非平稳或从非平稳向平稳变点的变点,这使得关于持久性变点的检验问题受到统计学和计量经济学等领域的广泛关注,如Hakkio和Rush [1] 发现美国财政赤字数据中存在一个由平稳过程到单位根过程变化的持久性变点,Kim [2] [3] 等提出了一种残差比率统计量来检验由平稳过程向单位根过程变化以及从单位根过程向平稳过程变化的持久性变点,Perron [4] [5] 研究了具有结构变点的单位根检验问题,并提出Dickey-Fuller (DF)检验统计量。传统的DF单位根检验法应用到持久性变点检验问题中时,由于序列中单位根部分支配渐进性导致渐进分布不会随着样本大小而发散到负无穷,因此传统的DF检验无法区分从单位根过程向平稳过程变化的持久性变化变点。为此,Banerjee等 [6] 在单位根过程原假设下提出了能够检验持久性变点的修正DF统计量。Leybourne等 [7] 指出Banerjee等 [6] 构造的Dickey-Fuller型统计量存在不足,即当检测序列整段为平稳过程时检测结果仍然显示序列存在持久性变点,为此,Leybourne等 [7] 提出了一种 Dickey-Fuller比率统计量来解决此问题,结果表明Dickey-Fuller比统计量不论在单位根原假设还是平稳原假设下都不会出现拒绝原假设,认为数据中存在持久性变点的问题,且在备择假设下能够很好的检测这两个方向变化的持久性变点。
上述这些研究都只考虑的是单位根过程和短记忆平稳过程之间变化的持久性变点检验问题。由于在短记忆平稳过程和单位根过程之间还存在一类更为广泛的分整过程(或称为长记忆过程),这使得单位根过程、短记忆过程及分整过程间变化变点的检验问题也收到广泛关注,如Hassler和Scheithauer [8] 基于Kim [2] 提出的比率统计量研究了从短记忆过程向长记忆过程变化变点的检验问题,Sibbertsen和Kruse [9] 在长记忆过程原假设下基于一种平方CUSUM方法研究了持久性变点的检验问题。本文基于Dickey-Fuller比统计量研究从单位根过程向分整过程以及从分整过程向单位根过程变化变点的检验检验。
由于Dickey-Fuller比统计量的临界值不可避免的会依赖长记忆参数值,为方便实际应用,本文提出通过Sieve Bootstrap方法来近似检验统计量的临界值。Sieve Bootstrap方法由Buhlmann [10] 于1997年首次提出,Poskitt [11] 指出Sieve Bootstrap方法在分整过程分析中有非常好的结果,Kapetanios [12] 提出了适用于分析非平稳长记忆时间序列的Sieve Bootstrap方法。Chen等 [13] 将Sieve Bootstrap方法应用到长记忆时间序列方差变点检验问题,Chen等 [14] [15] 基于Sieve Bootstrap方法进一步研究了从短记忆过程向长记忆过程变化变点,以及从平稳长记忆过程向非平稳长记忆过程变化变点的检验问题,收到了较好的效果。本文数值模拟结果表明,基于Sieve Bootstrap方法确定的临界值在单位根及分整过程原假设下都能很好的控制检验水平,且在备择假设下对两个方向变化变点都有较高的检验势。
2. 模型与假设检验
本文考虑如下分整模型:
其中n为样本容量,L是滞后算子, 为长记忆参数, 为独立同分布随机变量,且 , , 与 间的关系可被表示如下:
其中 ;当 时 为平稳序列, 时序列 为非平稳序列,特别地当 时序列 是一个单位根过程。
记 。
本文研究以下两类变点检验问题:
1) 序列 从 向 变化的持久性问题假设检验,即检验原假设
备择假设
2) 序列 从 向 变化的持久性问题假设检验,即检验原假设
备择假设
其中 为未知变点位置, 表示取整数部分。
为了检验上述两类假设检验问题,采用Leubourne和Toylor [7] 提出的Dickey-Full比统计量:
其中 , , 且 , , , 。
对于给定区间 ,统计量的值定义为: ,在原假设 下,当 的值小于临界值时拒绝原假设 ,认为数据中存在从 向 变化的持久性变点;在原假设 下,当 大于给定临界值时拒绝原假设 ,认为数据中存在从 向 变化的持久性变点。
3. Bootstrap方法
本文采用Rambaccussing [16] 提出的分数阶差分Sieve Bootstrap方法来近似临界值,其步骤如下:
1) 估计 的长记忆参数 ,并记估计值为 。
2) 对 进行 阶差分, 。其中 , 。
3) 对 进行重抽样,得到新的序列 。
4) 生成Bootstrap样本
,其中
,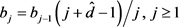 ,
,
是独立同分布的标准正态分布随机序列。
5) 计算统计量 ,重复步骤3~5 B次,取 的 分位数作为检验统计量在显著水平a
下的临界值。
4. 数值模拟
本节通过数值模拟检验所提方法的有效性,所有模拟通过R语言程序3.4.0版本下实现。数据由 模型生成,样本量n取200和500,长记忆参数 分别取0.2,0.4,0.6和0.8,变点位置 , 分别取0.25,0.5和0.75,Sieve Bootstrap循环次数B = 199,检验水平取10%和5%,长记忆参数的估计方法使用Robinson [17] 提出的Local Whittle估计,所得模拟结果都经过2000次循环得到。
表1给出了统计量 在200和500样本量下的经验水平,由结果可以看出:统计量在 取0.2,0.4和1时可以很好的控制经验水平, 取0.6和0.8时略高于检验水平,在500样本量下所得经验水平更加接近检验水平,结果说明Sieve Bootstrap方法可以有效的近似统计量的临界值。
表2给出了检验统计量在 和 下的经验势,由结果可以看出:在 下随着 取值的增大检验势变低, 取0.2时更容易检测到变点,随着 增大到0.8时检验势递减到最低,说明当长记忆参数间隔越大越容易检测到变点。例如 , ,5%检验水平下统计量在不同变点位置的检验势分别为96.7%,98.4%,32.3%,而 时检验势分别为14.9%,24.8%和13%。变点位置同样对检验结果有显著影响,当 时检验势要高于 和 ,但在 和 时的检验结果较为接近,而当变点位置 时检验势较低,这说明统计量 对位置比较靠前的变点具有较好的检验效果,而当变点位置靠后时检测效果较差。在 下,统计量 检验势结果同
Table 1. Empirical sizes of Ξ n ( X ) (%)
表1. 的经验水平(%)
Table 2. Power values of Ξ n ( X ) (%)
表2. 的检验势(%)
样具有上述性质,但在 取0.6和0.8且变点位置靠后时几乎检测不到变点。此外,随着样本容量的增大检验统计量在所有情况下的检验势都显著提高,这说明该方法是检验这两类变点问题的一致方法。比较两种备择假设下的检验势可以发现,对于相同跳跃度的变点统计量 更容易检测到从单位根过程向分整过程变化的变点,这也符合DF统计量最初的设计是为了在单位根原假设下做检验的特点。
5. 总结
本文基于Dickey-Fuller比率统计量研究了分别以单位根过程和分整过程为原假设下的持久性变点的检验问题,并提出通过Sieve Bootstrap方法近似检验统计量的临界值来方便实际应用。数值模拟结果说明:Sieve Bootstrap方法在单位根过程和分整过程两种原假设下近似的临界值结果都能够很好的控制经验水平;在两种备择假设下,当长记忆参数间隔越大检验统计量越容易检验到变点,比较靠前的变点具有较好的检验效果,而当变点位置靠后时检检验效果较差。而对于相同跳跃度的变点,DF统计量在检验从单位根过程向分整过程变化的持久性变点时的效果要优于检验从分整过程向单位根过程变化的持久性变点时的效果。
致谢
本文是在我的导师陈占寿教的指导下完成的,陈占寿教授本着严谨的科学态度,一毫不苟的学术精神,悉心育人。在此感谢陈占寿教授对我学业上的指导与关心,同时还要感谢国家自然科学青年基金、青海省自然科学青年基金对我的资助。
基金项目
国家自然科学青年基金(11301291, 11661067),青海省自然科学基金(2015-ZJ-717)。
文章引用
何明灿,付国龙. 单位根过程与分整过程间变化变点的Sieve Bootstrap检验
Sieve Bootstrap Test for Changes between Unit Root Process and Fractional Integrated Processes[J]. 统计学与应用, 2018, 07(02): 111-116. https://doi.org/10.12677/SA.2018.72014
参考文献
- 1. Hakkio, A.W. and Rush, M. (1991) Is the Budget Deficit Too Large? Econometrics Inquiry, 29, 429-445.
- 2. Kim, J.Y. (2000) Detection of Change in Persistence of Linear Times Series. Journal of Econometrics, 95, 97-116. https://doi.org/10.1016/S0304-4076(99)00031-7
- 3. Kim, J.Y., Belaire Franch, J. and Badilli Amador, R. (2002) Corri-gendum to “Detection of Change in Persistence of Linear Times Series”. Journal of Econometrics, 109, 389-392. https://doi.org/10.1016/S0304-4076(02)00087-8
- 4. Perron, P. (1989) The Great Crash, the Oil Price Shock, and the Unit Root Hypothesis. Econometrica, 57, 1361-1401. https://doi.org/10.2307/1913712
- 5. Perron, P. (1990) Testing for a Unit Root in a Time Series with a Changing Mean. Journal of Business & Economic Statistics, 8, 153-162.
- 6. Anindya, Banerjee, Lumsdaine, R. and Stock, J. (1992) Recursive and Sequential Tests of the Unit-Root and Trend-Break Hypotheses: Theory and International Evidence. Journal of Business & Economic Statistics, 10, 271-287.
- 7. Leybourne, S.J., Kim, T.H. and Taylor, A.M.R. (2006) Regression-Based Tests for a Change in Persistence. Oxford Bulletin of Economics & Statistics, 68, 595-621. https://doi.org/10.1111/j.1468-0084.2006.00179.x
- 8. Hassler, U. and Scheithauer, J. (2011) Detecting Changes from Short to Long Memory. Statistical Paper, 52, 847-870. https://doi.org/10.1007/s00362-009-0292-y
- 9. Sibbertsen, P. and Kruse, R. Testing for a Break in Persistence under Long-Range Dependencies.
- 10. Buhlmann, P. (1997) Sieve Bootstrap for Time Series. Bernoulli, 3, 123-148. https://doi.org/10.2307/3318584
- 11. Poskitt, D.S. (2008) Properties of the Sieve Bootstrap for Fractionally Integrated and Non-Invertible Processes. Journal of Time Series Analysis, 29, 224-250. https://doi.org/10.1111/j.1467-9892.2007.00554.x
- 12. Kapetanios, G. (2010) A Generalization of a Sieve Bootstrap In-variance Principle to Long Memory Processes. Quantitative and Qualitative Analysis in Social Sciences, 4, 19-40.
- 13. Chen, Z., Tian, Z., Xiao, Q. and Xing, Y. (2014) Sieve Bootstrap Test for Variance Change in Long Memory Time Series. International Joint Conference on Applied Mathematics, 41, 61-73.
- 14. Chen, Z., Tian, Z. and Xing, Y. (2016) Sieve Bootstrap Monitoring Per-sistence Change in Long Memory Process. Statistics & Its Interface, 9, 37-45. https://doi.org/10.4310/SII.2016.v9.n1.a4
- 15. Chen, Z., Xing, Y. and Li, F. (2016) Sieve Bootstrap Monitoring for Change from Short to Long Memory. Economics Letters, 140, 53-56. https://doi.org/10.1016/j.econlet.2015.12.023
- 16. Rambaccussing, D. (2015) A Test of the Long Memory Hypothesis Based on Self-Similarity. Journal of Time Series Econometrics, Sire Discussion Papers, 7.
- 17. Robinson, P.M. (1995) Gaussian Semiparametric Estimation of Long Range Dependence. Annals of Statistics, 23, 1630-1661. https://doi.org/10.1214/aos/1176324317
