Advances in Condensed Matter Physics
Vol.06 No.03(2017), Article ID:21887,7
pages
10.12677/CMP.2017.63010
Geometric Phase in a Generalized Jaynes-Cummings Model with Double Mode Operators and Phase Operators
Yuanxin Qiao, Zhaoxian Yu
Department of Physics,

Received: Aug. 15th, 2017; accepted: Aug. 25th, 2017; published: Aug. 31st, 2017

ABSTRACT
By using the Lewis-Riesenfeld invariant theory, the geometric phase in a generalized Jaynes-Cummings model with double mode operators and phase operators has been studied. Compared with the dynamical phase, the geometric phase in a cycle case is independent of the frequency of the double photon field, the coupling coefficient between photons and atoms, and the atom transition frequency. It is apparent that the geometric phase has the pure geometric and topological characteristics, which means that the geometric phase represents the holonomy in the Hermitian linear bundles.
Keywords:Geometric Phase, Lewis-Riesenfeld Invariant Theory, Generalized Jaynes-Cummings Model
具有双模运算符和相位运算符的广义Jaynes-Cummings模型中的几何相位
乔元新,于肇贤
北京信息科技大学理学院,北京
收稿日期:2017年8月5日;录用日期:2017年8月25日;发布日期:2017年8月31日

摘 要
通过使用Lewis-Riesenfeld不变理论,已经研究了具有双模运算符和相位运算符的广义Jaynes-Cummings模型中的几何相位。与动力学相位相比,一个周期情况下的几何相位与双光子场的频率无关,光子和原子之间的耦合系数以及原子跃迁频率。显然,几何相具有纯几何和拓扑特征,这意味着几何相位代表了厄米线性束中的和乐。
关键词 :几何相位,Lewis-Riesenfeld不变理论,广义Jaynes-Cummings模型

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
众所周知,Pancharatnam [1] 首先引入几何相位的概念来研究古典光在不同极化状态下的干扰。Berry [2] 在循环绝热演化的情况下发现了Pancharatnam相位的量子对应物。Ahyalov和Anandan [3] 对其扩展到了非绝热循环演化。Samuel等人 [4] 通过扩展到非循环演化和顺序投影测量来研究纯态几何相位的一般性。几何相位是量子运动学的结果,因此与状态空间中的路径的动态起源的详细性质无关。Mukunda和Simon [5] 通过将在状态空间中穿过的路径作为几何相位的主要概念给出了运动学方法。通过放宽绝热条件,统一性和演化的循环性,进行了进一步的推广和改进 [6] 。最近,混合状态的几何相位也已经被研究 [7] [8] [9] 。
我们知道Lewis和Riesenfeld [10] 提出的量子不变性理论是用于处理与时间相关的哈密顿量系统的强大工具。通过引入基本不变量的概念的一般性,并用于研究几何相位 [11] [12] [13] [14] ,与时间相关的薛定谔方程的精确解。Berry相位的发现不仅是旧的量子绝热近似理论的突破,也为我们许多物理现象提供了新见解。Berry相位的概念已经不同的方向得到发展 [15] - [23] 。
自从几何相位发现以来,它对物理理论和应用均产生了重大影响。一方面,其理论层面的研究十分广泛,包含:绝热和循环过程、非绝热和非循环的推广、混态、非对角项、开放系统以及它与微分几何和规范场理论的广泛联系。另一方面,它的应用几乎触及了物理研究的方方面面,例如:分子物理学、凝聚态以及量子信息与计算。其次,量子精确和准精确可解问题无论从理论物理学家还是实验物理学家的角度看都有重要的意义,因为其理论计算的结论可以和实验的结果直接对照。最后,狭义相对论的理论结论超越我们日常的经验而且几乎不可能在平常的低速实验中得到观察,例如:运动的尺缩短和运动的钟变慢等现象。所以,借助于光学实验验证它的结论变得非常有意义。
在本文中,通过Lewis-Riesenfeld不变量理论,我们将研究具有双模运算符和相位运算符的广义Jaynes-Cummings模型中的几何相位。这对在凝聚态和量子光学中的新奇现象发现有一定的理论意义。
2. 模型
具有双重模式运算符和相位运算符的广义Jaynes-Cummings模型中的哈密顿量被描述为 [24]
 (1)
(1)
其中 (
(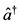 )和
)和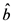 (
( )是双光子湮灭(产生)运算符。
)是双光子湮灭(产生)运算符。 (
(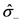 )是原子定义
)是原子定义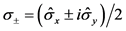 的伪旋律运算符,其中
的伪旋律运算符,其中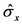 和
和 是保利矩阵,
是保利矩阵, 代表原子和光场之间的耦合强度,
代表原子和光场之间的耦合强度,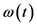 是电磁波的频率,
是电磁波的频率,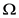 是原子的跃迁频率。
是原子的跃迁频率。
我们介绍以下运算符:
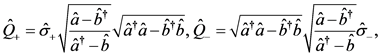 (2)
(2)
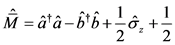 (3)
(3)
还有以下对易关系:
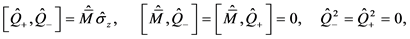 (4)
(4)
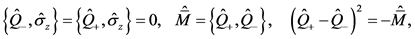 (5)
(5)
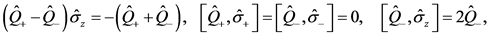 (6)
(6)
 (7)
(7)
其中{,}代表反对易括号。方程(1)式变为
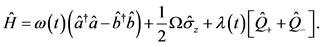 (8)
(8)
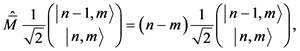 (9)
(9)
所以我们可以把我们的研究限制在我们在超对称准正弦矩阵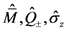 和
和 的希尔伯特空间,随后,我们用特定的特征值
的希尔伯特空间,随后,我们用特定的特征值 来代替运算符
来代替运算符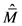 。
。
3. 量子系统的几何相因子
我们首先说明了Lewis-Riesenfeld(L-R)不变量理论 [10] 。对于与时间相关的一维系统其哈密顿量 则存在称为不变量
则存在称为不变量 的运算符将会满足方程式,
的运算符将会满足方程式,
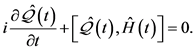 (10)
(10)
给出与时间有关的不变量 的特征值方程
的特征值方程
 (11)
(11)
当 。该系统与时间相关的薛定谔方程为
。该系统与时间相关的薛定谔方程为
 (12)
(12)
根据L-R不变理论,等式(12)的特解 与关于
与关于 的本征函数
的本征函数 只有相位因子
只有相位因子 不同,即
不同,即
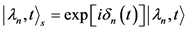 (13)
(13)
这表明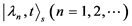 形成方程(12)解的完整集合。然后可以把(12)的薛定谔方程的一般解写为下列形式
形成方程(12)解的完整集合。然后可以把(12)的薛定谔方程的一般解写为下列形式
 (14)
(14)
此时
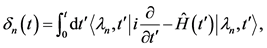 (15)
(15)
并且 。
。
对于(8)式的哈密顿量描述的系统,我们可以定义以下不变量
 (16)
(16)
将方程(8)和方程(16)带入方程(10),得到一个辅助方程
 (17)
(17)
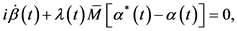 (18)
(18)
其中,dot表示时间导数, 表示算子
表示算子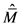 的特征值。
的特征值。
为了获得与时间无关的不变量我们可以引入单位变换 当满足以下关系时,很容易发现
当满足以下关系时,很容易发现
 (19)
(19)
和
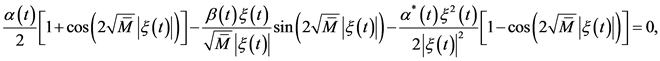 (20)
(20)
得到与时间无关的不变量
 (21)
(21)
根据方程(19),我们可以选择
 (22)
(22)
根据方程(22),在方程(16)中的不变量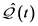 变为
变为
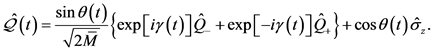 (23)
(23)
通过使用Baker-Campbell-Hausdoff公式 [25]
 (24)
(24)
通过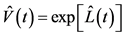 ,当满足下列等式时,很容易得到
,当满足下列等式时,很容易得到
 (25)
(25)
有
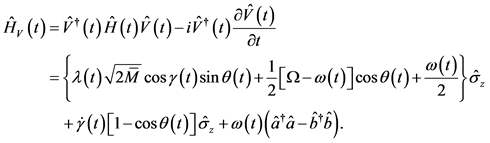 (26)
(26)
对于,方程(12)有一个的具体解:
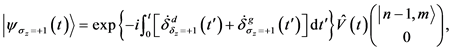 (27)
(27)
其中
 (28)
(28)
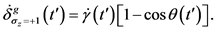 (29)
(29)
对于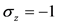 ,有
,有
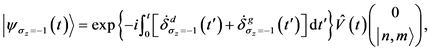 (30)
(30)
此时
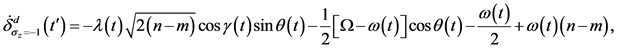 (31)
(31)
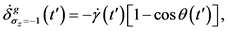 (32)
(32)
从等式(28)~(29),(31)~(32)我们得出结论,当 ,系统的动力学和几何相位因子分别为
,系统的动力学和几何相位因子分别为 和
和 。特别地,当我们考虑不变量
。特别地,当我们考虑不变量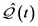 的参数空间中的周期,并且使
的参数空间中的周期,并且使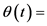 常数时,从式(29)和(32)分别得到一个方程,
常数时,从式(29)和(32)分别得到一个方程,
 (33)
(33)
这里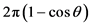 表示不变量
表示不变量 的参数空间上的立体角。
的参数空间上的立体角。
4. 结论
本文通过使用Lewis-Riesenfeld不变量理论,研究了具有双模运算符和相位运算符的广义Jaynes-Cummings模型中的几何相位。与动力学相位相比,一个周期情况下的几何相位与双光子场的频率无关,包括光子和原子之间的耦合系数以及原子跃迁频率。很明显,几何相具有纯粹的几何和拓扑特征。
基金项目
本文得到北京信息科技大学研究生院基金支持。
文章引用
乔元新,于肇贤. 具有双模运算符和相位运算符的广义Jaynes-Cummings模型中的几何相位
Geometric Phase in a Generalized Jaynes-Cummings Model with Double Mode Operators and Phase Operators[J]. 凝聚态物理学进展, 2017, 06(03): 74-80. http://dx.doi.org/10.12677/CMP.2017.63010
参考文献 (References)
- 1. Gao, X.C., Xu, J.B. and Qian, T.Z. (1991) Geometric Phase and the Generalized Invariant Formulation. Physical Review A, 44, 7016. https://doi.org/10.1103/PhysRevA.44.7016
- 2. Yu, G., Yu, Z.X. and Zhang, D.X. (1996) Berry Phase of the Finite Deep Column Potential Well with Motive Boundary. Yantai Teachers University Journal, 12, 117.
- 3. Gao, X.C. et al. (1996) Quantum-Invariant Theory and the Evolution of a Quantum Scalar Field in Robertson-Walker Flat Spacetimes. Physical Review D Particles & Fields, 53, 4374. https://doi.org/10.1103/PhysRevD.53.4374
- 4. Hou, Y.Z., Yu, Z.X. and Liu, Y.H. (1994) Using Quantum-Positive Transformations to Cause the Scalability of Topological Items to Obtain the Perturbation of Perturbation on the Contribution of Berry Phase factors. Journal of Xinyan Teachers College, 7, 37.
- 5. Liang, J.Q. and Ding, X. (1991) Broken Gauge Equivalence of Hamiltonians Due to Time-Evolution and the Berry Phase. Physics Letters A, 153, 273-278. https://doi.org/10.1016/0375-9601(91)90942-2
- 6. Sun, C.P. and Ge, M.L. (1990) Generalizing Born-Oppenheimer Approximations and Observable Effects of an Induced Gauge Field. Physical Review D Part Fields, 41, 1349-1352. https://doi.org/10.1103/PhysRevD.41.1349
- 7. Berry, M.V. (1984) Quantal Phase Factors Accompanying Adibatic Changes. Proceedings of the Royal Society of Lon-don, 392, 45-57. https://doi.org/10.1098/rspa.1984.0023
- 8. Sun, C.P. (1993) Quantum Dynamical Model for Wave-Function Re-duction in Classical and Macroscopic Limits. Physical Review A, 48, 898. https://doi.org/10.1103/PhysRevA.48.898
- 9. Aharonov, Y. and Bohm, D. (1959) Significance of Electromagnetic Potentials in the Quantum Theory. Physical Review, 115, 485-491. https://doi.org/10.1103/PhysRev.115.485
- 10. Aharonov, Y. and Anandan, J (1987) Phase Change during a Cyclic Quantum Evolution. Physical Review Letters, 58, 1953. https://doi.org/10.1103/PhysRevLett.58.1593
- 11. Sun, C.P. (1988) Analytic Treatment of High-Order Adiabatic Approx-imations of 2-Neutrino Oscillations in Matter. Physical Review D Particles & Fields, 38, 2908-2910. https://doi.org/10.1103/PhysRevD.38.2908
- 12. Samuel, J. and Bhandari, R. (1988) General Setting for Berry’s Phase. Physical Review Letters, 60, 2339. https://doi.org/10.1103/PhysRevLett.60.2339
- 13. Sun, C.P. et al. (1988) High-Order Quantum Adiabatic Approximation and Berry’s Phase Factor. Journal of Physics A General Physics, 21, 1595. https://doi.org/10.1088/0305-4470/21/7/023
- 14. Yu, Z.X. and Zhang, D.X. (1995) Phase Factor for Quantum Systems with Time-Bound Condition. Journal of Qingdao University, 8, 49.
- 15. Chen, J.Q., Li, J. and Liang, Q. (2006) Critical Property of the Geo-metric Phase in the Dicke Model. Physical Review A, 74, 150. https://doi.org/10.1103/PhysRevA.74.054101
- 16. Pati, A.K. (1995) Geometric Aspects of Noncyclic Quantum Evolution. Physical Review A, 52, 2576-2584. https://doi.org/10.1103/PhysRevA.52.2576
- 17. Fan, H.Y. and Ruan, T.N. (1984) Some New Applications of Co-herent States. China Science, 42, 27.
- 18. Tsui, D.C., et al. (1982) Two-Dimensional Magnetotransport in the Extreme Quantum Limit. Physical Review Letters, 48, 1559-1562. https://doi.org/10.1103/PhysRevLett.48.1559
- 19. Semenoff, G.W., et al. (1986) Non-Abelian Adiabatic Phases and the Fractional Quantum Hall Effect, Physical Review Letters, 57, 1195-1198. https://doi.org/10.1103/PhysRevLett.57.1195
- 20. Chen, C.M., et al. (1991) Quantum Hall Effect and Bery Phase Factor Physics. Acta Physica sinica, 40, 345
- 21. Fan, H.Y. and Li, L.S. (1996) Supersymmetric Unitary Operator for Some Generalized Jaynes-Cummings Models Communications in Theoretical Physics, 25, 105. https://doi.org/10.1088/0253-6102/25/1/105
- 22. Uhlmann, A (1986) Parallel Transport and Quantum Holonomy along Density Operators. Reports on Mathematical Physics, 24, 229-240. https://doi.org/10.1016/0034-4877(86)90055-8
- 23. Wu, Y. and Yang, X. (1997) Jaynes-Cummings Model for a Trapped Ion in Any Position of a Standing Wave. Physical Review Letters, 78, 3086-3088. https://doi.org/10.1103/PhysRevLett.78.3086
- 24. Sjoqvist, E. et al. (2000) Geometric Phases for Mixed States in In-terferometry. Physical Review Letters, 85, 2845- 2849. https://doi.org/10.1103/PhysRevLett.85.2845
- 25. Lewis, H.R. and Riesenfeld, W.B. (1969) An Exact Quantum Theory of the Time-Dependent Harmonic Oscillator and of a Charged Particle in a Time-Dependent Electromagnetic Field. Jour-nal of Mathematical Physics, 10, 1458-1473. https://doi.org/10.1063/1.1664991