Artificial Intelligence and Robotics Research
Vol.
08
No.
01
(
2019
), Article ID:
28965
,
12
pages
10.12677/AIRR.2019.81004
Matrix Completion Based on Weighted Truncated Schatten-p Norm and Improved Second Order Total Variation
Gang Chen
School of Mathematics and Statistics, Southwest University, Chongqing

Received: Jan. 24th, 2019; accepted: Feb. 13th, 2019; published: Feb. 22nd, 2019

ABSTRACT
In recent years, matrix completion problem has attracted researchers’ interest in many practical applications. A lot of matrix completion methods based on low rank matrix recovery theory have been developed. In these methods, only the low rank prior information of matrices is considered. However, in the practical application of matrix completion, the local smooth priori information has not been better utilized, which leads to poor matrix completion effect. To solve the above problems, this paper proposes a matrix completion model based on weighted truncated Schatten-p norm and improved second-order total variation. This model uses weighted truncated Schatten-p norm to constrain the matrix with low rank prior. The smooth prior of the matrix is modeled by the improved second-order total variation norm. Compared with the experimental results of many existing matrix completion methods in text mask image reconstruction, the proposed method has better completion effect.
Keywords:Matrix Completion, Weighted Truncated Schatten-p Norm, Smooth Prior, Improved Second-Order Total Variation
基于加权截断Schatten-p范数 与改进二阶全变分的矩阵填充
陈刚
西南大学,数学与统计学院,重庆

收稿日期:2019年1月24日;录用日期:2019年2月13日;发布日期:2019年2月22日

摘 要
近年来,矩阵填充问题在许多实际应用中引起了研究人员的广泛关注,并产生了一些基于低秩矩阵恢复理论的矩阵填充方法。在这些方法中,人们一般只关注于矩阵的低秩先验信息部分。但是,在矩阵填充的实际应用中,局部光滑先验信息却没有得到更好的利用,使得实际应用中的矩阵填充效果往往不佳。针对上述问题,本文提出了基于加权截断Schatten-p范数与改进二阶全变分的矩阵填充模型。该模型利用加权截断Schatten-p范数对矩阵进行低秩约束,同时利用改进的二阶全变分范数对矩阵的光滑先验信息进行建模,以此来提高矩阵填充效果。通过与多种已有的常用矩阵填充方法在文本掩膜图像重建中的实验结果对比,所提出的方法具有更好的矩阵填充效果。
关键词 :矩阵填充,加权截断Schatten-p范数,光滑先验,改进二阶全变分

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
矩阵填充(Matrix completion)是指对于一个元素缺失的矩阵,通过对其有效位置的元素进行采样,进而恢复出缺失的元素。近年来,矩阵填充问题已经受到学者们的广泛关注并已被有效应用于图像修复 [1] [2] [3] [4] 和机器学习 [5] [6] [7] [8] [9] 等领域。在许多的实际应用场景下,我们需要进行填充的矩阵一般都是低秩的或者是可以用低秩矩阵逼近的。因此,矩阵填充问题通常都可以通过低秩建模为以下优化问题 [4] :
(1)
其中, , 表示秩函数。在矩阵M中,只有在地址集合 中的元素存在,而在其它位置的元素未知。
然而,由于秩函数是非凸且不连续的,所以式(1)是一个NP难问题,难以求解。为了解决这一问题,文献 [4] [10] 中提出利用核范数来逼近矩阵的秩,从而将式(1)转化为如下凸优化问题:
(2)
其中, 表示矩阵X的核范数, 表示X的第i个最大的奇异值。
虽然核范数能够很好的逼近非凸的秩函数,且文献 [4] 中给出了很强的理论保证,但其和秩函数的最佳逼近函数还有一定差距,所以在实际应用中其所获结果往往不是最优的。这是由于矩阵的每一个非零奇异值对秩函数来说是同等重要的,而核范数定义为全部非零奇异值之和,并且同时最小化,这样就使得每一个奇异值具有了不相同的贡献。所以不能将核范数作为秩函数的最佳逼近函数。近些年来,为了能够更精确的逼近秩函数,学者们提出了一些更优的秩函数的逼近函数。NIE [11] 等人提出Schatten-p范
数来作为秩函数的逼近函数,其具体表示为 。由此可知,当参数 时,Schatten-p范数即等价于核范数,而当p越趋近于0时,则Schatten-p范数对秩函数的逼近能力越强。Hu [12] 等人在2013年提出定义为 的截断核范数(Truncated Nuclear Norm,简写为TNN)
模型同时也被称作奇异值部分和模型 [13] (partial sum of singular values,简写为PSSV)。该模型的主要思想是去除前r个较大奇异值,以减小由奇异值差别过大从而对低秩部分造成的干扰。GU [14] 等人提出加
权核范数(Weighted Nuclear Norm),其定义为 ,相比于核范数而言,其采用对奇异
值加权的方式改变不同奇异值对秩函数的影响,从而获得了对秩函数更好的逼近效果。之后,在加权核范数和Schatten-p范数的提出与应用的基础上,Xie [15] 等人提出了加权Schatten-p范数,其表达式为
, ,并指出该范数可以更精确的逼近秩函数。
然而,几乎所有现存的矩阵填充方法都是专注于矩阵的低秩这一全局先验信息,从而寻求一个秩函数的最佳逼近函数。在实际应用,除了低秩这一全局先验信息外矩阵中往往还存在结构先验信息,例如,图像的局部光滑先验信息。Han在文献 [16] 中首次将上述两种先验信息同时用于矩阵填充问题,提出了基于核范数和线性全变分的矩阵填充方法(LTVNN),该方法相比基于核范数的方法可以获得更好的矩阵填充效果。但LTVNN方法受线性全变分的影响,图像容易产生阶梯效应。Wang在文献 [17] 提出了一种改进的二阶全变分范数(Modified Second-Order Total Variation),该范数更充分的利用了图像的局部光滑这一结构先验信息,其可以很好的克服线性全变分方法所产生的阶梯效应。
受上述思想启发,我们结合加权Schatten-p范数和截断核范数的优点,提出了一个基于加权截断Schatten-p范数与改进二阶全变分的矩阵填充模型(WTP-MSTVM),该模型利用加权截断Schatten-p范数对矩阵低秩先验信息建模,同时利用改进二阶全变分范数对矩阵局部光滑先验信息建模。然后采用交替方向乘子法设计了一个高效的算法对模型进行优化求解,最后,通过文本掩膜图像重建实验来说明我们提出方法的优势。
2. WTP-MSTVM模型的建立
本文提出了一种同时利用矩阵低秩与光滑先验信息的矩阵填充模型(WTP-MSTVM),该模型的表达式如下所示:
(3)
其中 表示采用加权截断Schatten-p范数进行低秩约束。 为X的改进的二阶全变分范数,是对矩阵光滑先验信息的约束, 为正则化参数。下面将详细介绍模型(3)的各项含义。
2.1. 低秩正则化约束
在矩阵填充问题中,所求矩阵一般是低秩的或者是可以用低秩矩阵来逼近的。因此,本文此采用加权截断Schatten-p范数来精确刻化出矩阵的秩,其模型如下所示:
(4)
其中 为X的第i个奇异值,且奇异值的大小为降序排列,r为截断阈值, 为其对应第i个奇异值的权重, 为加权Schatten-p范数的参数。为了能够让(4)式尽最大可能逼近秩函数,权重参数 和截断阈值r的取值非常重要,本文通过设计一个非递减的自适应更新的权重公式,使得所有的非零奇异值在加权后贡献近似相等,该权重公式如下式所示:
(5)
其中常数 , 是为了防止分母为零而设置。而对于r的选择,我们可以尝试所有可能r值,选则效果最好的作为其最终值,根据文献 [12] 可知,在绝大多数情况下,测试1至20间的值即足够了。
2.2. 改进二阶全变分正则约束
由于全变分范数容易产生阶梯效应 [18] ,为了更好的利用光滑先验信息,我们采用改进的二阶全变分范数对光滑性进行约束,其定义如下:
(6)
其中
(7)
(8)
显然,本文的改进的二阶全变分范数充分利用了点
周围邻近四个点即
,
,
,
的信息,其相比传统的二阶全变分 [19] 和只用到一个点周围邻近两个点即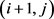 ,
的线性全变分可以得到更好的效果,因为其不但继承了传统二阶全变分的几何结构,而且克服了线性全变分容易产生阶梯效应的这一缺陷。利用其建模的函数是光滑函数也可以让我设计出更高效的数值求解算法。为便于设计优化求解算法,(6)式可改写为如下形式:
,
的线性全变分可以得到更好的效果,因为其不但继承了传统二阶全变分的几何结构,而且克服了线性全变分容易产生阶梯效应的这一缺陷。利用其建模的函数是光滑函数也可以让我设计出更高效的数值求解算法。为便于设计优化求解算法,(6)式可改写为如下形式:
(9)
其中对于
(10)
所以,本文提出的基于加权Schatten-p范数与改进二阶全变分的矩阵填充模型(3)可改写为如下优化问题:
(11)
3. WTP-MSTVM模型的求解
针对优化问题(11),我们采用交替方向乘子法 [20] [21] (ADMM)来对其进行其优化求解,该方法已经被广泛应用于优化问题的求解中。首先,引入拉格朗日乘子Z,问题(11)可以转化为如下相等的问题:
(12)
则式(12)相应的增广拉格朗日函数如下所示:
(13)
其中, 是惩罚参数, 是拉格朗日乘数。目标函数(13)可以通过ADMM方法在选定一个变量的同时固定其他变量来迭代更新求解,确切的说,在第 次迭代时,变量的更新求解步骤描述如下:
1) 固定变量Z和A,更新X
(14)
根据参考文献 [12] 可知,加权截断Schatten-p范数可转化为如下加权Schatten-p范数形式:
(15)
其中 分别为左奇异特征向量和右奇异特征向量。故(14)式可改写为:
(16)
定义 ,问题(16)可通过参考文献 [15] 中的引理来求解。
引理1:已知矩阵Q的奇异值分解为
,
,则(16)式的最优解为
,其中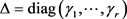 是如下优化问题的解:
是如下优化问题的解:
(17)
利用广义软阈值算法(Generalized Soft-Thresholding,简写为GST)求解(17)中的子问题,其阈值算子为
(18)
如果 ,那么 。否则, 。该阈值算法的更多细节推到详见参考文献 [15] 。
2) 固定变量X和A,更新Z
(19)
令 ,令式(15)关于Z的倒数为零可得下式:
(20)
其中 是 的单位矩阵,等式(20)是著名的Sylvester等式 [22] ,可通过MATLAB命令𝑙𝑦𝑎𝑝对其直接求解,即
(21)
在获得 后,我们便可求得式(19)的解即:
(22)
3) 固定X和Z,更新A:
(23)
我们将上述迭代过程总结为如下算法1
4. 仿真实验结果及分析
矩阵填充方法通常被应用于文本掩膜图像重建问题中。在本节中,为了说明我们提出模型的优势,我们将本文提出的WTP-MSTVM模型与现存的另外5种表现出色的矩阵填充模型在上述应用中的实验结果来进行对比。这5种模型分别是IRLS [23] 、PSSV [13] 、LTVNN [16] 、SPC-TV [24] 和SPC-QV [25] 。实验选取了16张大小为 像素的图像处理领域被广泛使用的图片(图1)来生成所需的测试数据,被文本掩膜覆盖后的图像如图2所示。本文所有仿真实验环境为Intel(R) Core i5-4430 CPU @ 2.70 GHz处理器,在内存为4 GB,win10操作系统的计算机,MATLAB版本为R2016a上运行。
我们采用图像处理领域常用的两个指标信噪比(PSNR)和结构相似性(SSIM)指标来评估被各模型重建图像的质量。参考文献 [23] 有SSIM的详细定义,PSNR的定义如下所示:
(24)
其中 , 表示 中元素的个数,M和 分别表示原始图像和重建后的图像。上述两个指标都是值越大表示图像重建效果越好。

Figure 1. The 16 test images, all are numbered in order from 1 to 16, from left to right, and from top to bottom
图1. 16张测试图,图片从左到右,从上到下依次编号为1至16

Figure 2. Images are covered by the same text mask
图2. 被同一文本掩膜覆盖效果图
4.1. 参数p的选取
为了得到模型参数 的最优值,我们选取[0.05,0.95]中间间隔0.1的10个值以及1共11个值作为p的取值,每个p值在上述16张图像上的实验所得PSNR平均值与SSIM平均值如图3和图4所示:
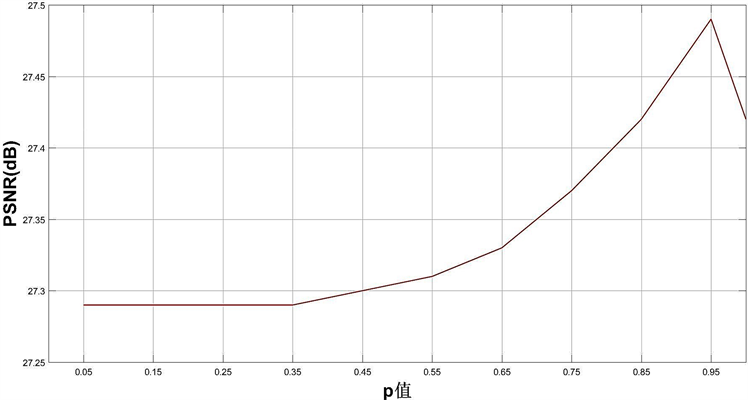
Figure 3. The effect of different p values on the mean PSNR of 16 test images
图3. 不同p的取值对16张测试图PSNR平均值的影响

Figure 4. The effect of different p values on the mean SSIM of 16 test images
图4. 不同p的取值对16张测试图SSIM平均值的影响
从图3中可以看出当p取值为0.95时实验所得PSNR平均值最大,效果最好。而从图4中可以看到,对于SSIM平均值而言,p的取值对其影响不大,所以在本文下面的实验中,我们统一将p取值为0.95。
4.2. 仿真实验结果及分析
文本掩膜图像重建问题实现起来是非常困难的,因为被文本覆盖的像素点并不是随机分布在矩阵中的,并且有可能有重要结构信息被掩盖了。在处理这一问题时,我们可以先检测出被文本覆盖的像素的位置,然后将其视作缺失值,这样该问题便转化为矩阵填充问题。
Table 1. Reconstructing results by the above algorithms (PSNR/SSIM)
表1. 通过上述各种算法重建结果(PSNR/SSIM)
Continued
表1是本文提出模型与另外5种模型在16张测试图像上实验的PSNR与SSIM指标的实验结果,从中我们可以看出,本文提出的模型在除第15张图片外,其实验所得PSNR值都为最大,且在SSIM值上我们的模型在所有情况下都为最优,在第1张图片上我们的模型所获PSNR值比表现第二好的SPC-QV模型多出接近4 dB,这对图像处理来说是一个很大的提升,而本文提出模型在所有图片的PSNR结果平均值(AVE)也比第二高的模型SPC-QV多出接近1.4 dB。我们提出模型的SSIM平均值也比表现第二好的SPC-QV的平均值高出0.01,而比IRLS的SSIM平均值高出0.07。
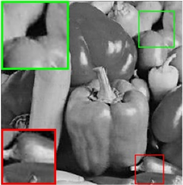
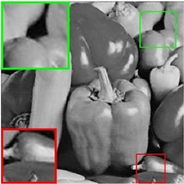
图5和图6分别是第16张和第14张图片经过各种算法进行文本掩膜重建后的视觉效果图,就视觉效果而言,本文提出模型很好的将原图像重建了出来。从图5和图6的放大窗口中我们可以看到,我们的模型对图像的细节恢复更好并且几乎看不到有任何的文本覆盖痕迹,而经过IRLS和PSSV模型重建的结果则相对较差,还留有明显的文本痕迹。经过LTVNN重建的结果存在阶梯效应的影响,而SPC-QV
 (a) 原图
(a) 原图
 (b) 文本覆盖
(b) 文本覆盖
 (c) IRLS
(c) IRLS
 (d) PSSV
(d) PSSV
 (e) LTVNN
(e) LTVNN
 (f) SPC-TV
(f) SPC-TV
 (g) SPC-QV
(g) SPC-QV
 (h) WTP-MSTVM
(h) WTP-MSTVM
Figure 5. The 16th image is reconstructed by different algorithm. (a) The original image. (b) Text masked image. (c) IRLS: PSNR = 22.14 dB, SSIM = 0.90. (d) PSSV: PSNR = 24.41 dB, SSIM = 0.93. (e) LTVNN: PSNR = 25.33 dB, SSIM = 0.96. (f) SPC-TV: PSNR = 25.33 dB, SSIM = 0.94. (g) SPC-QV: PSNR = 27.07 dB, SSIM = 0.97. (h) WTP-MSTVM: PSNR = 29.20 dB SSIM = 0.98
图5. 第16张图片通过各算法重建视觉效果图。(a) 原图。(b) 文本覆盖。(c) IRLS:PSNR = 22.14 dB,SSIM = 0.90。(d) PSSV:PSNR = 24.41 dB,SSIM = 0.93。(e) LTVNN:PSNR = 25.33 dB,SSIM = 0.96。(f) SPC-TV:PSNR = 25.33 dB,SSIM = 0.94。(g) SPC-QV:PSNR = 27.07 dB,SSIM = 0.97。(h) WTP-MSTVM:PSNR = 29.20 dB,SSIM = 0.98
 (a) 原图
(a) 原图
 (b) 文本覆盖
(b) 文本覆盖
 (c) IRLS
(c) IRLS
 (d) PSSV
(d) PSSV
 (e) LTVNN
(e) LTVNN
 (f) SPC-TV
(f) SPC-TV
 (g) SPC-QV
(g) SPC-QV
 (h) WTP-MSTVM
(h) WTP-MSTVM
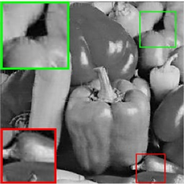
Figure 6. The 14th image is reconstructed by different algorithm. (a) The original image. (b) Text masked image. (c) IRLS: PSNR = 21.43 dB, SSIM = 0.90. (d) PSSV: PSNR = 24.76 dB, SSIM = 0.93. (e) LTVNN: PSNR = 25.19 dB, SSIM = 0.97. (f) SPC-TV: PSNR = 25.13 dB, SSIM = 0.94. (g) SPC-QV: PSNR = 27.20 dB, SSIM = 0.97. (h) WTP-MSTVM: PSNR = 29.76 dB SSIM = 0.99
图6. 第14张图片通过各算法重建视觉效果图。(a) 原图。(b) 文本覆盖。(c) IRLS:PSNR = 21.43 dB,SSIM = 0.90。(d) PSSV:PSNR = 24.76 dB,SSIM = 0.93。(e) LTVNN:PSNR = 25.19 dB,SSIM = 0.97。(f) SPC-TV:PSNR = 25.13 dB,SSIM = 0.94。(g) SPC-QV:PSNR = 27.20 dB,SSIM = 0.97。(h) WTP-MSTVM:PSNR = 29.76 dB,SSIM = 0.99
模型所得结过虽然要比SPC-TV的好,但仍然存在一些模糊的文字痕迹。所以,总的来说,我们所提出的模型WTP-MSTVM展示了其优秀的矩阵填充性能,在产生最高的PSNR与SSIM指标结果的同时也拥有一个更加让人满意的矩阵填充效果。
5. 总结与展望
本文在同时考虑矩阵低秩先验与光滑先验信息的同时,提出了基于加权截断Schatten-p范数与改进二阶全变分的矩阵填充模型(WTP-MSTVM)。采用加权截断Schatten-p范数对图像的低秩先验信息进行约束,对于光滑先验信息则采用改进的二阶全变分范数进行约束。通过实验结果证明,本文提出的模型不管是在定量的数值结果上还是在视觉效果上都要优于现存的多种矩阵填充模型。在未来的工作中,我们将考虑寻求更优的秩函数逼近函数以及尝试加入其它更多的先验信息到我们的模型当中,以此来获得更好的矩阵填充效果。
基金项目
课题由中央高校基本科研业务费资助项目(No.XDJK2018C076)资助。
文章引用
陈 刚. 基于加权截断Schatten-p范数与改进二阶全变分的矩阵填充
Matrix Completion Based on Weighted Truncated Schatten-p Norm and Improved Second Order Total Variation[J]. 人工智能与机器人研究, 2019, 08(01): 24-35. https://doi.org/10.12677/AIRR.2019.81004
参考文献
- 1. Cabral, R., Del, T., Costeira, P., et al. (2015) Matrix Completion for Weakly-Supervised Multi-Label Image Classification. IEEE Transactions on Pattern Analysis & Machine Intelligence, 37, 121-135. https://doi.org/10.1109/TPAMI.2014.2343234
- 2. Yong, L., Liu, T., Tao, D., et al. (2015) Multiview Matrix Completion for Multilabel Image Classification. IEEE Transactions on Image Processing, 24, 2355-2368. https://doi.org/10.1109/TIP.2015.2421309
- 3. Recht, B., Fazel, M. and Parrilo, P.A. (2010) Guaranteed Minimumrank Solu-tions of Linear Matrix Equations via Nuclear Norm Minimization. SIAM Review, 52, 471-501. https://doi.org/10.1137/070697835
- 4. Nie, F., Huang, H. and Ding, C. (2012) Low Rank Matrix Recovery via Efficient Schatten-p Norm Minimization. Proceedings of the 26th AAAI Conference on Artificial Intelligence, Toronto, Ontario, Canada: AAAI Press, 655-661.
- 5. Hu, Y., Zhang, D., Ye, J., et al. (2013) Fast and Accurate Matrix Completion via Truncated Nuclear Norm Regularization. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35, 2117-2130. https://doi.org/10.1109/TPAMI.2012.271
- 6. Oh, T., Tai, Y., Bazin, J., Kim, H. and Kweon, I. (2016) Partial Summinimization of Singular Values in Robust PCA: Algorithm and Applications. IEEE Transactions on Pattern Analysis and Machine Intelligence, 38, 744-758. https://doi.org/10.1109/TPAMI.2015.2465956
- 7. Komodakis. N. (2006) Image Completion Using Global Optimization. Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, 17-22 June 2006, 442-452. https://doi.org/10.1109/CVPR.2006.141
- 8. Keshavan, H. and Montanari, S. (2010) A Matrix Completion from a Few Entries. EEE Transactions on Information Theory, 56, 2980-2998. https://doi.org/10.1109/TIT.2010.2046205
- 9. Li, W., Zhao, L., Lin, Z., et al. (2015) Non-Local Image Inpainting Using Low-Rank Matrix Completion. Computer Graphics Forum, 34, 111-122. https://doi.org/10.1111/cgf.12521
- 10. Cand`es, E.J. and Recht, B. (2009) Exact Matrix Completion via Convex Optimization. Foundations of Computational Mathematics, 9, 717-772. https://doi.org/10.1007/s10208-009-9045-5
- 11. Yu, T., Yan, J., Liu, W. and Li, B. (2018) Incremental Multi-Graph Matching via Diversity and Randomness Based Graph Clustering. Proceedings of the European Conference on Computer Vision (ECCV), Munich, 8-14 September 2018, 139-154. https://doi.org/10.1007/978-3-030-01261-8_9
- 12. Yu, T. Yan, J., Zhao, J., et al. (2018) Joint Cuts and Matching of Partitions in One Graph. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, 18-23 June 2018, 705-713. https://doi.org/10.1109/CVPR.2018.00080
- 13. Koren, Y., Bell, R. and Volinsky, C. (2009) Matrix Factorization Techniques for Recommender Systems. The Computer Journal, 42, 30-37.
- 14. Gu, S., Xie, Q., Meng, D., et al. (2017) Weighted Nuclear Norm Minimization and Its Applications to Low Level Vision. International Journal of Computer Vision, 121, 183-208. https://doi.org/10.1007/s11263-016-0930-5
- 15. Xie, Y., Gu, S., Liu, Y., et al. (2016) Weighted Schatten p-Norm Minimization for Image Denoising and Background Subtraction. IEEE Transactions on Image Processing, 25, 4842-4857. https://doi.org/10.1109/TIP.2016.2599290
- 16. Han, X., Wu, J., Wang, L., Chen, Y. and Shu, H. (2014) Linear Total Variation Approximate Regularized Nuclear Norm Optimization for Matrix Completion. Abstract and Applied Analysis, 2014, Article ID: 765782. https://doi.org/10.1155/2014/765782
- 17. Wang, W. and Wang, J. (2018) Enhancing Matrix Completion Using a Modified Second-Order Total Variation. Discrete Dynamics in Nature and Society, 2018, Article ID: 2598160. https://doi.org/10.1155/2018/2598160
- 18. Rodriguez, P. (2013) Total Variation Regularization Algorithms Forimages Corrupted with Different Noise Models: A Review. Journal of Electrical and Computer Engineering, 2013, Article ID: 217021.
- 19. Papafitsoros, K., Schoenlieb, C.B. and Sengul, B. (2013) Combined First and Second Order Total Variation in Painting Using Split Bregman. Image Processing on Line, 3, 112-136. https://doi.org/10.5201/ipol.2013.40
- 20. Boyd, S., Parikh, N., Chu, E., Peleato, B. and Eckstein, J. (2011) Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations and Trends in Machine Learning, 3, 1-122. https://doi.org/10.1561/2200000016
- 21. Lin, Z., Liu, R. and Su, Z. (2011) Linearized Alternating Direction Method with Adaptive Penalty for Low-Rank Representation. Proceedings of the 25th Annual Conference on Neural Information Processing Systems, Granada, 12-15 December 2011, 1-7.
- 22. Benner, P., Li, R.C. and Truhar, N. (2009) On the ADI Method for Sylvester Equations. Journal of Computational and Applied Mathematics, 233, 1035-1045. https://doi.org/10.1016/j.cam.2009.08.108
- 23. Lai, M.J., Xu, Y.Y. and Yin, W.T. (2013) Improved Iteratively Reweighted Least Squares for Unconstrained Smoothed l𝑞 Minimization. SIAM Journal on Numerical Analysis, 51, 927-957. https://doi.org/10.1137/110840364
- 24. Wang, Z., Bovik, A.C., Sheikh, H.R. and Simoncelli, E.P. (2004) Image Quality As-sessment: Fromerror Visibility to Structural Similarity. IEEE Transactions on Image Processing, 13, 600-612. https://doi.org/10.1109/TIP.2003.819861
- 25. Yokota, T., Zhao, Q. and Cichocki, A. (2016) Smooth PARAFAC Decomposi-tion for Tensor Completion. IEEE Transactions on Signal Processing, 64, 5423-5436. https://doi.org/10.1109/TSP.2016.2586759
