Advances in Applied Mathematics
Vol.06 No.04(2017), Article ID:21279,6
pages
10.12677/AAM.2017.64052
Multivariate Lagrange Interpolation Defined on Ellipsoidal Surface
Tingting Hui, Haibo Liu, Lihong Cui
Liaoning Normal University, Dalian Liaoning
Received: Jun. 15th, 2017; accepted: Jul. 3rd, 2017; published: Jul. 6th, 2017

ABSTRACT
The multivariate Lagrange interpolation problem, which is usually defined on the ellipsoid, is often studied in practical scientific research and production. Multivariate Lagrange interpolation is proposed to define the definition of ellipsoid and given to determine whether the node group on an ellipsoid form judgment theorem and superposition method to construct interpolation regular set of nodes and finally is to implement the method.
Keywords:Ellipsoid, Multivariate Lagrange Interpolation, Regular Set of Nodes, Superposition Interpolation Method
定义于椭球面上的多元Lagrange插值问题研究
惠婷婷,刘海波,崔利宏
辽宁师范大学,辽宁 大连
收稿日期:2017年6月15日;录用日期:2017年7月3日;发布日期:2017年7月6日

摘 要
针对在实际科研生产中经常涉及到的有关定义于椭球面上的多元Lagrange插值问题进行了研究。提出了定义于椭球面上的多元Lagrange插值定义,给出了判定椭球面上的结点组是否构成插值正则结点组的判定定理以及迭加构造方法,最后通过算例对所得方法进行了实现。
关键词 :椭球面,多元Lagrange插值,正则结点组,迭加插值法

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
熟知,多元函数插值长期以来一直是计算数学研究领域的一个主要研究内容(详见文献 [1] ),有关多元函数插值基本理论和方法研究中一个基本问题是多元插值函数的唯一存在性问题,也就是插值的正则性问题。由文献 [2] - [8] 可知,国内外学者对这一问题的研究主要有两个判别,一种是给定插值空间,去构造相应正则结点组;另一种是给定结点组,去构造相应正则插值空间,而且要求空间的次数尽可能低。 [9] [10] [11] ,对于某一类问题,目前,有关在整个空间进行插值以及关于定义于空间中一般代数流形插值的研究结果相对完备,而关于有着重要实用价值的具体流形上的插值结果并不多见。梁学章等人 [12] 讨论了单位球面上的纬线组选取插值正则结点组的方法。
椭球面是除球面外的另一类主要的二次代数曲面,其在工程设计中有着重要的作用。例如,许多机械零部件和建筑外形采用了椭球面的形式,而地球本身严格来讲是个椭球,还有就是有关对地球表面进行卫星遥感测绘时也涉及到椭球面上插值问题。因此,对椭球面上的插值问题研究意义重大。
2. 基本定义和基本定理
本文主要研究三维欧式空间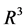 中的椭球面
中的椭球面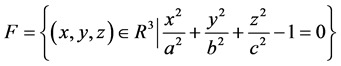 上进行多元Lagrange插值问题。
上进行多元Lagrange插值问题。
首先引入若干基本概念
设n为非负整数,令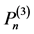 表示所有全次数为n的三元代数多项式构成的集合,即
表示所有全次数为n的三元代数多项式构成的集合,即 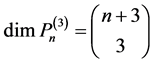
定义1 (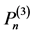 的插值正则结点组)
的插值正则结点组)
设 ,令
,令 为
为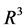 中m个互异点构成的点集,如果对于任意给定的数组
中m个互异点构成的点集,如果对于任意给定的数组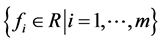 ,恒存在唯一多项式
,恒存在唯一多项式 ,使之满足:
,使之满足: ,则称
,则称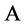 为
为 的一个正则结点组。
的一个正则结点组。
定义2 ( 上的插值正则结点组)
上的插值正则结点组)
设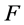 为如上所定义的椭球面,
为如上所定义的椭球面,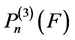 为
为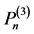 在
在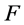 上的限制。
上的限制。 ,
, ,称
,称 为定义于
为定义于 上的一个n次插值正则结点组,如果对于任意给定的数组
上的一个n次插值正则结点组,如果对于任意给定的数组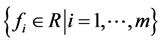 ,恒存在多项式
,恒存在多项式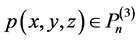 ,满足
,满足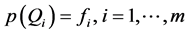 。
。
定理1 (构造 插值正则结点组的添加椭球面法)
插值正则结点组的添加椭球面法)
设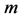 为如上所定义,
为如上所定义, ,结点组
,结点组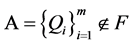 关于
关于 的一个正则结点组,而
的一个正则结点组,而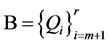 是定义于
是定义于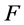 的一个
的一个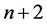 次正则结点组,则
次正则结点组,则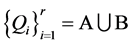 必定构成
必定构成 的正则结点组。
的正则结点组。
证明:设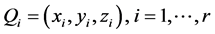 。因为
。因为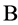 为定义于
为定义于 上的
上的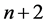 次正则结点组,由定义2,对任意给定数组
次正则结点组,由定义2,对任意给定数组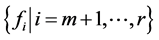 恒存在多项式
恒存在多项式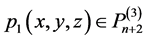 使得
使得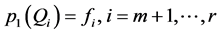 。
。
又因为 关于
关于 的一个正则结点组,由定义1对任意的数组
的一个正则结点组,由定义1对任意的数组 恒存在多项式
恒存在多项式 使得
使得
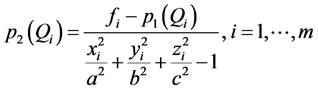
其中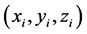 为
为 的三维坐标,构造一个多项式
的三维坐标,构造一个多项式

显然有 且满足
且满足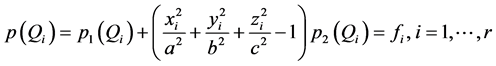 。
。
则由定义1知,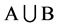 为
为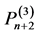 的正则结点组。
的正则结点组。
定理2 (构造 上插值正则结点组添加圆锥曲线法)
上插值正则结点组添加圆锥曲线法)
设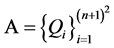 为
为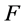 上的
上的 次插值正则结点组,平面
次插值正则结点组,平面 与
与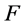 横截相交于圆周曲线
横截相交于圆周曲线 ,
,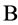 是定义于
是定义于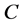 上的一个
上的一个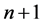 次正则结点组,则
次正则结点组,则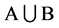 必定构成定义于
必定构成定义于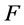 上的一个
上的一个 次正则结点组。
次正则结点组。
定理3 (判定定理)
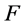 上的
上的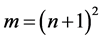 个互异点
个互异点 能够做成定义于
能够做成定义于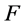 上的n次插值正则结点组的充分必要条件是,若存在
上的n次插值正则结点组的充分必要条件是,若存在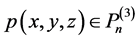 ,满足
,满足 ,蕴含如此的
,蕴含如此的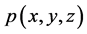 在
在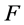 恒为零。
恒为零。
证明:充分性:设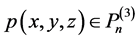 ,满足
,满足 ,
,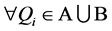 由条件可知,
由条件可知,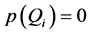 ,
, 。从而,对于定义于
。从而,对于定义于 的一个n次插值正则结点组
的一个n次插值正则结点组 ,亦有
,亦有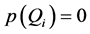 ,
, ,即
,即 ,
, 。又因为
。又因为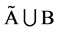 为
为 的插值正则结点组,故
的插值正则结点组,故 。
。
必要性:令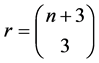 ,取
,取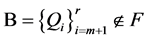 为关于
为关于 的正则结点组,可以断言:
的正则结点组,可以断言: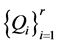 构成
构成 的正则结点组。事实上,对任给
的正则结点组。事实上,对任给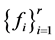 ,由于
,由于 为定义
为定义 上的
上的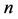 次正则结点组,故存在多项式
次正则结点组,故存在多项式 满足
满足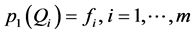 。
。
又因为 且为关于的
且为关于的 的正则结点组,则存在多项式
的正则结点组,则存在多项式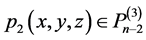 满足
满足
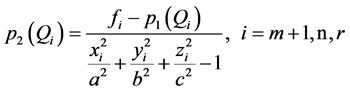
则多项式 (*)
(*)
满足 ,由定义知
,由定义知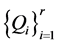 是
是 的正则结点组,同时,在上述过程中取
的正则结点组,同时,在上述过程中取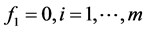 ,则(*)式中的
,则(*)式中的 ,此时
,此时
满足定理中的插值条件的多项式,故由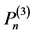 空间中满足相同插值条件的多项式的唯一存在性有
空间中满足相同插值条件的多项式的唯一存在性有
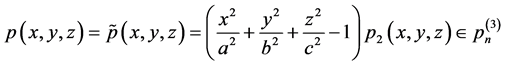
即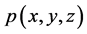 在
在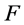 上恒为零值。
上恒为零值。
3. 算例
例如:取被插值函数为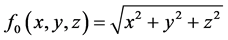 ,椭球面为
,椭球面为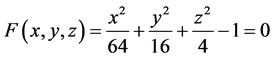 。在椭
。在椭
球内部取一点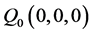 ,则该点为
,则该点为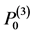 的一个正则结点组;另在椭球面上取互异的9个点
的一个正则结点组;另在椭球面上取互异的9个点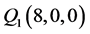 ,
,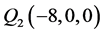 ,
,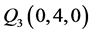 ,
, ,
,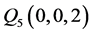 ,
,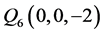 ,
, ,
,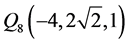 ,
,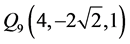 ,这九个点是定义于椭球面F上的一个
,这九个点是定义于椭球面F上的一个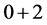 次正则结点组(如图1所示),则由定理1知:点组
次正则结点组(如图1所示),则由定理1知:点组 构成
构成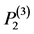 适定结点组。设插值多项式为
适定结点组。设插值多项式为
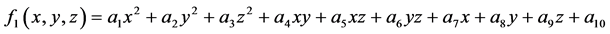
得到方程组为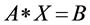 ,其中
,其中

Figure 1. Point of the ellipsoid
图1. 椭球面取点效果图

解得
我们取点 ,
,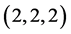 ,插值结果分别为
,插值结果分别为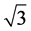 ,
,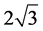 ,而精确值分别为
,而精确值分别为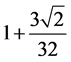 ,
, ,误差分别为
,误差分别为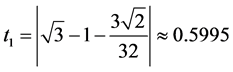 ,
, 。
。
致谢
这次论文能够顺利的完成,得力于老师和同学的帮助和辅导,所以在这里我要表达我的感激之情。
首先我要感谢我的论文指导老师,崔利宏老师以及刘海波同学。本文是在导师崔利宏教授的悉心指导和严格要求下完成的。感谢老师为我提供了论文材料,耐心为我讲解疑难问题,指明方向。每一个环节导师都倾注了大量的时间和心血。导师和蔼可亲,遇到问题总是耐心讲解,他的严谨求实的治学态度、诲人不倦的精神,对我的影响深远而广泛,使我在做文和做人方面终身受益。在此,我向我的导师致以深深的谢意。最后,向在百忙中抽出时间对本文进行评审并提出宝贵意见的各位专家表示衷心地感谢!
基金项目
辽宁省大学生实践基地建设项目,辽教[2015]399号;辽宁省教育厅科研项目,L201683661。
文章引用
惠婷婷,刘海波,崔利宏. 定义于椭球面上的多元Lagrange插值问题研究
Multivariate Lagrange Interpolation Defined on Ellipsoidal Surface[J]. 应用数学进展, 2017, 06(04): 442-447. http://dx.doi.org/10.12677/AAM.2017.64052
参考文献 (References)
- 1. Carnicer, J.M. and Gasca, M. (2010) Multivariate Polynomial Interplation: Some New Trends. Monogr Real Acad Cienc Zaragoza, 33, 197-208.
- 2. 梁学章. 关于多元函数的插值与逼近[J]. 高等学校计算数学学报, 1979(1): 123-124.
- 3. 梁学章. 二元插值的适定结点组与迭加插值法[J]. 吉林大学自然科学学报, 1979(1): 27-32.
- 4. Liang, X.Z., Lv, C.M. and Feng, R.Z. (2001) Properly Posed Sets of Nodes for Multivariate Lagrange Interpolation in . SIAM Journal on Numerical Analysis, 30, 581-595. https://doi.org/10.1137/s0036142999361566
- 5. 梁学章, 张洁琳, 崔利宏. 多元Lagrange插值与Cayley-Bacharach定理[J]. 高等数学计算数学学报, 2005(27): 276-281.
- 6. Liang, X.Z.,Wang, R.H., Cui, L.H., et al. (2006) Some Researches on Trivariate Lagrange Interpolation. Journal of Computational and Applied Mathematics, 195, 192-205. https://doi.org/10.1016/j.cam.2005.03.083
- 7. 梁学章, 张明, 张洁琳, 等. 高维空间中代数流形上多项式空间的维数与Lagrange插值适定结点组的构造[J]. 吉林大学学报(理学版), 2006(44): 309-317.
- 8. Liang, X.Z., Zhang, J.L., Zhang, M., et al. (2009) Superposition Interpolation Process in . Applied Mathematics and Computation, 215, 227-234. https://doi.org/10.1016/j.amc.2009.04.079
- 9. De Boor, C. and Ron, A. (1990) On Mutivariate Polynomial Interpolation. Constructive Approximation, 6, 287-302. https://doi.org/10.1007/BF01890412
- 10. Gasca, M. and Maeztu, J.I. (1982) On Lagrange and Hermite Interpolation in . Numerische Mathematik, 39, 1-14. https://doi.org/10.1007/BF01399308
- 11. Sauer, T. (1988) Polynomial Interpolation of Minimal Degree and Grobner Bases. In: London Mathematical Society Lecture Note Series, Vol. 251, Cambridge University Press, Cambridge, 483-494.
- 12. Liang, X.Z., Feng, R.Z. and Cui, L.H. (2000) Lagrange Interpolation on a Spherical Surface. Northeast Math J, 16, 243-252.