Advances in Applied Mathematics
Vol.07 No.03(2018), Article ID:24201,12
pages
10.12677/AAM.2018.73032
Mixed Finite Volume Element Method for Regularized Long Wave Burgers Equation
Xue Bai, Hong Li, Zhichao Fang
School of Mathematical Science, Inner Mongolia University, Hohhot Inner Mongolia
Received: Mar. 1st, 2018; accepted: Mar. 20th, 2018; published: Mar. 27th, 2018

ABSTRACT
The mixed finite volume element method for the regularized long wave Burgers equation is developed and studied. By introducing a transfer operator which maps the trial function space into the test function space, the semi-discrete and linear backward Euler fully discrete mixed finite volume element schemes are constructed. Stability analysis for semi-discrete scheme is given, the existence and uniqueness of the solutions are proved, and optimal error estimates for these schemes are obtained. Finally, numerical experiments are given to verify the theoretical results and the effectiveness of the proposed schemes.
Keywords:Mixed Finite Volume Element Method, Regularized Long Wave Burgers Equation, Optimal Error Estimate
正则长波Burgers方程的混合有限体积元方法
白 雪,李 宏,方志朝
内蒙古大学数学科学学院,内蒙古 呼和浩特
收稿日期:2018年3月1日;录用日期:2018年3月20日;发布日期:2018年3月27日

摘 要
本文研究了正则长波Burgers方程的混合有限体积元方法。引入迁移算子把试探函数空间映射为检验函数空间,构造了半离散和线性向后Euler全离散混合有限体积元格式,证明了两种离散格式解的存在唯一性,并得到了最优阶误差估计。最后,给出数值算例来验证理论分析结果和数值格式的有效性。
关键词 :混合有限体积元方法,正则长波Burgers方程,最优阶误差估计

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文考虑如下正则长波Burgers方程
(1)
其中
,
,
,系数
和s是给定的正常数。a和b分别为耗散系数和色散系数。
为给定的初始函数。
RLW-Burgers方程(1)又称为Benjamin-Bona-Mahony-Burgers方程,是带有耗散项
的正则长波方程,这类数学物理方程在非线性波问题中有着十分重要的地位。因此,求解此类问题的方法受到广泛的重视,文献 [1] 利用未知函数变换的思想,得到了RLW-Burgers方程的解析解,文献 [2] 运用一类含参数的G展开法得到了多种函数形式的显式行波解。这些解析解是在限定了初边值条件下给出的,因此研究该方程的数值计算方法是很有意义的。文献 [3] 研究了RLW-Burgers方程的有限差分法,给出了收敛性和稳定性分析。文献 [4] 构造了RLW-Burgers方程的H1-Galerkin混合有限元格式,给出了半离散和全离散格式的最优阶误差估计,并给出数值实验算例。文献 [5] 运用径向基函数法数值求解了高维广义Benjamin-Bona-Mahony-Burgers方程。
混合有限体积元方法又称为混合控制体积方法,最早是由Russel在文献 [6] 中求解线性椭圆问题时提出,随后文献 [7] [8] 通过数值实验验证该方法的可行性。Chou等人在文献 [9] [10] 中分别在三角形网格和矩形网格剖分下,使用最低阶Raviart-Thomas有限元空间作为试探函数空间,构造了椭圆方程的混合有限体积元格式并给出了最优阶误差估计。该方法不仅可以利用有限体积元方法的简便性同时求解多个不同的物理量,而且还可以保持某些物理量的局部守恒性,因此该方法自提出以来得到了很大的关注和发展,已经被用来求解二阶拟线性椭圆方程 [11] 、正则长波方程 [12] 、抛物方程 [13] [14] 、阻尼sine-Gordon方程 [15] 等数学物理方程。本文研究了RLW-Burgers方程(1)的混合有限体积元方法,构造了半离散和线性向后Euler全离散混合有限体积元格式,给出了理论分析并通过数值算例验证了方法的有效性。
本文余下部分安排如下:第2节,给出混合有限元形式,并引入迁移算子构造了半离散混合有限体积元格式;第3节,给出了迁移算子的一些性质,并给出半离散格式解的存在唯一性和稳定性以及误差估计;第4节,构造了线性向后Euler全离散格式,给出了全离散格式解的存在唯一性和最优阶误差估计;第5节,给出了数值算例验证该方法的有效性。本文理论分析时所用的C都是与空间网格参数h和时间离散步长
无关的正常数。
2. 半离散混合有限体积元形式
引入流量函数
,其中
,于是可以把原方程(1)改写为下面的形式
(2)
则相应的混合变分形式为:求
,使得
(3)
现在对区域
使用以下节点做原始网格剖分:
。对应的对偶网格剖分为:
,其中
。则原始网格剖分
。记
,
。假设
为拟一致剖分,即存在正常数a使得
。记
,
,
,则对偶剖分为
。基于剖分
,选取有限元空间
作为试探函数空间,其中
记
和
分别为有限元空间
和
的基,其中
是分段线性多项式(见文献 [12] ),
是集合
的特征函数。
定义迁移算子
如下
则有
。选取检验函数空间
为
的值域。系统(1)中(a)和(b)方程分别在对偶剖分和原始剖分上进行积分,得到
(4)
利用迁移算子
,可以把(4)改写为下列的形式:
(5)
注意到
(6)
通过计算可知
,利用形式(5)可以得到半离散混合有限体积元格式:求
,使得
(7)
其中
是椭圆投影算子,具体定义见第3节。
3. 半离散混合有限体积元形式的误差估计
为了进行误差估计,首先给出迁移算子
的性质。
引理3.1 [12] :迁移算子
是有界的,且满足
(8)
引理3.2 [12] :迁移算子
满足对称性,即有
(9)
引理3.3 [12] :迁移算子
满足下述正定性
(10)
引理3.4 [12] :设I是恒等算子,则迁移算子
满足下述性质
(11)
(12)
下面引入椭圆投影算子
,满足
其中
(13)
同时引入
正交投影算子
,满足
其中
(14)
由文献 [16] [17] 可知,对
,下列估计式成立
其中
(15)
其中
(16)
其中
(17)
利用算子
,可以得到下述引理。
引理3.5 [12] :存在与h无关的正常数C使得
(18)
(19)
为了对半离散格式进行误差估计,将误差写为
格式(3)和格式(7)作差,利用投影算子可得误差方程为
(20)
类似于文献 [12] 中的证明,可以得到下述半离散格式解的存在唯一性和稳定性。
定理3.1:半离散格式(7)存在唯一解
,且存在与h和t无关的正常数C,使得
下面给出半离散格式(7)的误差估计。
定理3.2:设
是混合变分形式(3)的解,
是半离散格式(7)的解,则存在与h和t无关的正常数C,使得
证明:在误差方程(20)中取
,则有
(21)
则由引理3.5及引理3.1,有
(22)
易知
。则(22)式可变为
(23)
对(23)两边关于t积分,可得
(24)
由Gronwall引理,可得
(25)
为估计
,在(20)中取
,则有
(26)
利用迁移算子的性质,并应用Cauchy-Schwarz不等式和Young不等式,可得
(27)
整理可得
(28)
将(25)式代入到(28)式,得到
(29)
为估计
,在(20)式中取
,则有
(30)
将(25)式和(29)式代入到(30)式,得到
(31)
最后利用投影估计和三角不等式完成定理的证明。
4. 全离散混合有限体积元格式的误差估计
令
是时间区域
的剖分,
,其中时间步长
,M是某一正整数。为了构造全离散格式,对于
上函数j,记
,
。并记
和
分别是u和p在
处的全离散解,现在给出线性向后Euler全离散混合有限体积元格式:求
,满足
(32)
首先给出全离散格式的解的存在唯一性证明。
定理4.1:设
和
是已知的,则线性向后Euler混合有限体积元格式(32)存在唯一解
。
证明:全离散格式(32)可以改写为,对
,有
(33)
(34)
由于
和
分别是有限元空间
和
的基函数,则
可以表示为
将上述表达式应用在(33)式和(34)式上,并取
,则全离散格式可以写为下述矩阵形式:求
,使得
(35)
其中
注意到矩阵A和D是对称正定矩阵,则(35)可变形为
(36)
其中
。当
充分小的时候,系统(36)的系数矩阵是可逆的,从而有唯一解,于是全离散格式(32)有唯一解。
下面给出全离散格式(32)的误差估计。将误差写为
将格式(7)与格式(32)作差,利用投影算子可得误差方程为
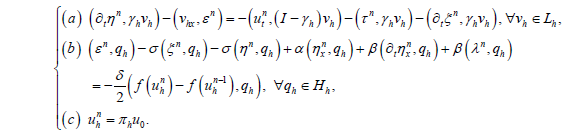 (37)
(37)
其中
。
定理4.2:设
是系统(32)的解,系统(3)的解
满足正则性质:
则存在与h和
无关的正常数C,使得
(38)
证明:在(37)中取
,得到
(39)
通过简单的计算,可知
(40)
(41)
应用上述不等式及Cauchy-Schwarz不等式和Young不等式,可得
(42)
通过计算可得
(43)
在(42)式两端同乘
,并令n由1到m求和,可得
(44)
注意到
,选取
满足
,应用引理3.3及离散的Gronwall引理,可知
(45)
下面来估计
,在(37)式中取
,可得
(46)
根据(43)式及引理3.1,可得
(47)
将式(45)代入式(47),可得
(48)
下面估计
。在(37)式中取
,利用引理3.1,可得
(49)
把(45)式和(48)式代入(49)式中,有
(50)
为了(45)式和(50)式的右端项,利用Taylor展开的积分余项公式,可以得到
最后使用上述不等式以及三角不等式完成定理的证明.
5. 数值算例
例1:本例考虑方程(1)中取
,计算区域
,
,初始函数
。空间和时间步长为
。图1为数值解
在时间
时的图像,图2为数值解
在时间
时的图像。
例2:文中的格式和理论分析的结果也适合于下述广义正则长波Burgers方程
(51)
在(51)中取
,计算区域
,
,初始函数
,源项函数
,则精确解为
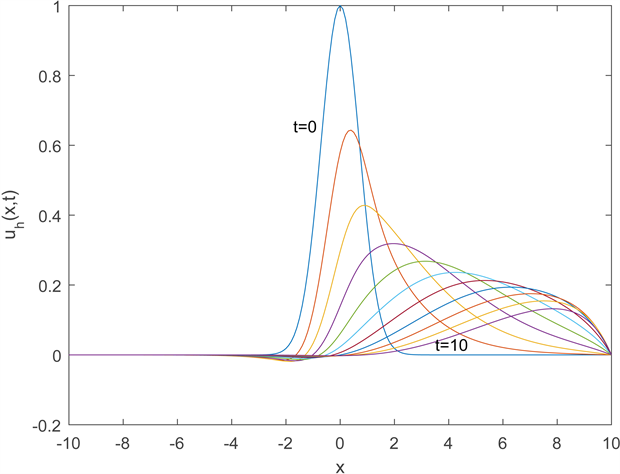
Figure 1. The numerical solution of uh(x,t)
图1. 数值解uh(x,t)
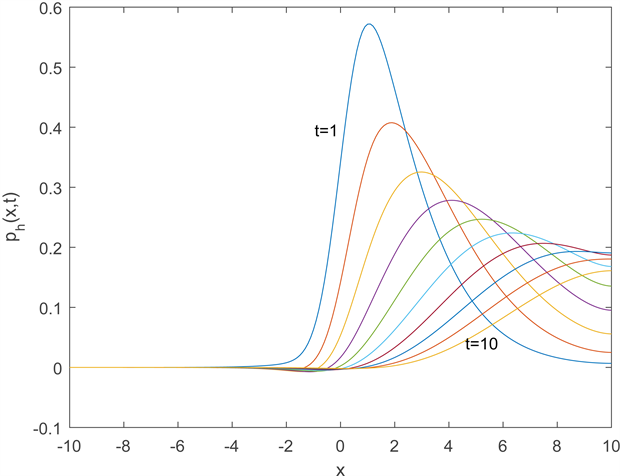
Figure 2. The numerical solution of ph(x,t)
图2. 数值解ph(x,t)

Table 1. Error estimate and order of convergence
表1. 误差估计和收敛阶
表1给出了上述广义正则长波Burgers方程(51)的混合有限体积元格式在不同的空间和时间等距剖分下的误差估计和收敛精度,可以看出收敛精度与理论分析结果是一致的,这表明混合有限体积元方法求解广义正则长波Burgers方程和正则长波Burgers方程是有效的。
基金项目
国家自然科学基金(11701299, 11761053),内蒙古自治区自然科学基金(2016BS0105, 2017MS0107),内蒙古自治区高等学校青年科技英才支持计划(NJYT-17-A07)。
文章引用
白 雪,李 宏,方志朝. 正则长波Burgers方程的混合有限体积元方法
Mixed Finite Volume Element Method for Regularized Long Wave Burgers Equation[J]. 应用数学进展, 2018, 07(03): 257-268. https://doi.org/10.12677/AAM.2018.73032
参考文献
- 1. 王明亮. RLW-Burgers方程的精确解[J]. 应用数学, 1995(1): 51-55.
- 2. 王鑫. RLW-Burgers方程的新显式行波解[J]. 应用数学进展, 2017(6): 619-626.
- 3. Zhao, X.H., Li, D.S. and Shi, D.M. (2008) A Finite Difference Scheme for RLW-Burgers Equation. Journal of Applied Mathematics & Informatics, 26, 573-581.
- 4. 刘洋. 非标准混合元方法分析及数值模拟[D]: [博士学位论文]. 呼和浩特: 内蒙古大学, 2011.
- 5. Dehghan, M., Abbaszadeh, M. and Mohebbi, A. (2014) The Numerical Solution of Nonlinear High Dimensional Generalized Benja-min-Bona-Mahony-Burgers Equation via the Meshless Method of Radial Basis Functions. Computers & Mathematics with Applications, 68, 212-237.
https://doi.org/10.1016/j.camwa.2014.05.019
- 6. Russell, T.F. (1995) Rigorous Block-Centered Discretizations on Irregular Grids: Improved Simulation of Complex Reservoir Systems. Technical Report No. 3, Project Report, Reservoir Simulation Research Corporation, Denver.
- 7. Jones, J.E. (1995) A Mixed Finite Volume Element Method for Accurate Computation of Fluid Velocities in Porous Media. Doctoral Thesis, Uni-versity of Colorado, Denver.
- 8. Cai, Z., Jones, J.E., Mccormick, S.F. and Russell, T.F. (1997) Control-Volume Mixed Finite Element Methods. Computers & Geosciences, 1, 289-315.
https://doi.org/10.1023/A:1011577530905
- 9. Chou, S.H., Kwak, D.Y. and Vassilevski, P.S. (1998) Mixed Covolume Methods for the Elliptic Problems on Triangular Grids. SIAM Journal on Numerical Analysis, 35, 1850-1861.
https://doi.org/10.1137/S0036142997321285
- 10. Chou, S.H. and Kwak, D.Y. (2000) Mixed Covolume Methods on Retangular Grids for Elliptic Problems. SIAM Journal on Numerical Analysis, 37, 758-771.
https://doi.org/10.1137/S0036142996305534
- 11. Kwak, D.Y. and Kim, K.Y. (2000) Mixed Covolume Methods for Quasi-Linear Second-Order Elliptic Problems. SIAM Journal on Numerical Analysis, 38, 1057-1072.
https://doi.org/10.1137/S003614299935855X
- 12. Fang, Z.C. and Li, H. (2013) Numerical Solutions of the Regularized Long Wave Equation Based on Mixed Covolume Method. Applied Mathematics and Mechanics, No. 34, 907-920.
- 13. Yang, S.X. and Jiang, Z.W. (2009) Mixed Covolume Method for Parabolic Problems on Triangular Grids. Applied Mathematics and Computation, No. 215, 1251-1265.
https://doi.org/10.1016/j.amc.2009.06.068
- 14. Rui, H.X. (2002) Symmetric Mixed Covolume Methods for Parabolic Problems. Numerical Methods for Partial Differential Equations, No. 18, 561-583.
- 15. Fang, Z.C. and Li, H. (2013) Mixed Covolume Methods for a Damped Sine-Gordon Equation on Triangular Grids. Advances in Mathematics, No. 42, 441-457.
- 16. Brezzi, F. and Fortin, M. (1991) Mixed and Hybrid Finite Element Methods. Springer-Verlag, New York.
https://doi.org/10.1007/978-1-4612-3172-1
- 17. Chen, Z.X. (2005) Finite Element Methods and Their Applica-tions. Springer-Verlag, Berlin.
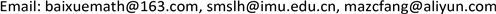





 (37)
(37)

