ABSTRACT

The equivalent condition and two sufficient conditions of complete convergence were obtained based on a monotone decreasing real sequence converging to 0, when the convergence of a random variables sequence was considered. At the same time, the related issues about almost sure convergence and convergence in probability were researched. The interrelations of these conditions were obtained and exemplified.

Keywords:Complete Convergence, Equivalent Condition, Sufficient Condition

随机变量序列完全收敛的等价及充分条件

袁代林

西南交通大学数学学院，四川 成都

收稿日期：2018年5月24日；录用日期：2018年6月12日；发布日期：2018年6月19日

摘 要

在随机变量序列收敛性的判断中，考虑了单调递减趋于0的实数数列，得到了随机变量序列完全收敛的等价条件和两个充分条件。同时研究了序列的几乎必然收敛和依概率收敛，用例子说明了这些条件之间的相互关系。

关键词 :完全收敛，等价条件，充分条件

Copyright © 2018 by author and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

随机变量序列完全收敛能推导出几乎必然收敛,几乎必然收敛能推导出依概率收敛 [1] 。目前有大量文章研究相依随机变量序列的收敛性问题，文献 [2] [3] 研究了有关混合序列加权和的完全收敛性，文献 [4] [5] [6] 研究了混合序列加权和的几乎必然收敛性。而对于一般的随机变量序列，文献 [7] 在研究几乎必然收敛时考虑了以单调递减趋于0的实数数列，得到判断几乎必然收敛的一个等价条件。

本文在研究随机变量序列的收敛性时，考虑了单调递减趋于0的实数数列。在考虑以单调递减趋于0的实数数列应用到完全收敛性的判断中，得到了判断完全收敛的一个等价条件，同时研究了完全收敛性判断的两个充分条件。这些研究都是针对一般的随机变量序列，没有独立性或同分布的要求。并且用简单的例子说明了这些条件之间的相互关系。

2. 随机变量序列收敛定义及相关定理

首先给出随机变量序列几种收敛的定义。

定义2.1 ( [1] ) 随机变量序列 $X_1,X_2,\cdots$ 依概率收敛到随机变量X，当且仅当下式成立

$\underset{n\to \infty }{\lim }P\left(\left|X_n-X\right|>\epsilon \right)=0,\forall \epsilon >0$ (1)

简记为 $X_n\stackrel{p}{\to }X$ 。

定义2.2 ( [1] ) 随机变量序列 $X_1,X_2,\cdots$ 几乎必然收敛到随机变量X，当且仅当下式成立

$P\left(\underset{n\to \infty }{\lim }{X}_n=X\right)=1$ (2)

简记为 $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X$ 。

定义2.3 ( [1] ) 随机变量序列 $X_1,X_2,\cdots$ 完全收敛到随机变量X，当且仅当下式成立

${\displaystyle \sum }_{n=1}^{\infty }P\left(\left|X_n-X\right|>\epsilon \right)<\infty ,\forall \epsilon >0$ (3)

简记为 $X_n\stackrel{\text{c}\text{.c}\text{.}}{\to }X$ 。

三种收敛性之间的关系是( [1] )

$X_n\stackrel{\text{c}\text{.c}\text{.}}{\to }X\Rightarrow X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X\Rightarrow X_n\stackrel{p}{\to }X$

下面定理 2.1 给出了几乎必然收敛的一些等价条件。

定理2.1 ( [1] ) $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X$ 与下面每个式子等价

$P\left({\displaystyle \underset{n=1}{\overset{\infty }{\cap }}{\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>\epsilon \right\}}}\right)=0,\forall \epsilon >0$ (4)

$\underset{n\to \infty }{\lim }P\left({\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>\epsilon \right\}}\right)=0,\forall \epsilon >0$ (5)

$P\left({\displaystyle \underset{k=1}{\overset{\infty }{\cup }}{\displaystyle \underset{n=1}{\overset{\infty }{\cap }}{\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>\frac{1}{k}\right\}}}}\right)=0$ (6)

$\underset{k\to \infty }{\lim }P\left({\displaystyle \underset{n=1}{\overset{\infty }{\cap }}{\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>\frac{1}{k}\right\}}}\right)=0$ (7)

$\underset{k\to \infty }{\lim }\underset{n\to \infty }{\lim }P\left({\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>\frac{1}{k}\right\}}\right)=0$ (8)

令正实数序列 ${\epsilon }_1,{\epsilon }_2,\cdots$ 单调递减以 0 为极限，容易证明下面关系式成立

${\displaystyle \underset{k=1}{\overset{\infty }{\cup }}{\displaystyle \underset{n=1}{\overset{\infty }{\cap }}{\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>\frac{1}{k}\right\}}}}={\displaystyle \underset{k=1}{\overset{\infty }{\cup }}{\displaystyle \underset{n=1}{\overset{\infty }{\cap }}{\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>{\epsilon }_k\right\}}}}$

由上式即得到下面的推论

推论2.2 $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X$ 与下面三个式子均等价

$\exists {\epsilon }_k\downarrow 0,\text{s}\text{.t}\text{.}P\left({\displaystyle \underset{k=1}{\overset{\infty }{\cup }}{\displaystyle \underset{n=1}{\overset{\infty }{\cap }}{\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>{\epsilon }_k\right\}}}}\right)=0$ (9)

$\exists {\epsilon }_k\downarrow 0,\text{s}\text{.t}\text{.}\underset{k\to \infty }{\lim }P\left({\displaystyle \underset{n=1}{\overset{\infty }{\cap }}{\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>{\epsilon }_k\right\}}}\right)=0$ (10)

$\exists {\epsilon }_k\downarrow 0,\text{s}\text{.t}\text{.}\underset{k\to \infty }{\lim }\underset{n\to \infty }{\lim }P\left({\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>{\epsilon }_k\right\}}\right)=0$ (11)

注2.1 当取 ${\epsilon }_k=\frac{1}{k}$ 时，(9)式即为(6)式，(10)式即为(7)式，(11)式即为(8)式。

考虑单调递减趋于0的实数数列，文献 [7] 给出了几乎必然收敛另外的等价条件。

定理2.3 ( [7] ) $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X$ 等价于

$\exists {\epsilon }_k\downarrow 0,\text{s}\text{.t}\text{.}\underset{n\to \infty }{\lim }P\left({\displaystyle \underset{k=n}{\overset{\infty }{\cup }}\left\{\left|X_k-X\right|>{\epsilon }_k\right\}}\right)=0$ (12)

值得注意的是，(12)式中随机变量序列 $\left\{X_k\right\}$ 的下标和正实数序列 $\left\{{\epsilon }_k\right\}$ 的下标有直接的关系，这不同于上面推论2.2中的三个式子。

由概率的连续性即得到 $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X$ 与下面式子等价

$\exists {\epsilon }_k\downarrow 0,\text{s}\text{.t}\text{.}P\left({\displaystyle \underset{n=1}{\overset{\infty }{\cap }}{\displaystyle \underset{k=n}{\overset{\infty }{\cup }}\left\{\left|X_k-X\right|>{\epsilon }_k\right\}}}\right)=0$ (13)

3. 主要结果及证明

如同几乎必然收敛的判定一样，在完全收敛的判定中引入单调递减趋于0的实数数列，得到下面的定理。

定理3.1 对随机变量序列 $X_1,X_2,\cdots$ 及随机变量X，有 $X_n\stackrel{\text{c}\text{.c}\text{.}}{\to }X$ 与下式等价

$\exists {\epsilon }_n\downarrow 0,\text{s}\text{.t}\text{.}{\displaystyle \sum _{n=1}^{\infty }P\left(\left|X_n-X\right|>{\epsilon }_n\right)}<\infty$ (14)

证“⟸”：因为存在使(14)式成立的数列 $\left\{{\epsilon }_n\right\}$ ， ${\epsilon }_n\downarrow 0$ ，所以对任意 $\epsilon >0$ ，必存在N，当 $n>N$ 时， ${\epsilon }_n<\epsilon$ 。由此得当 $n>N$ 时， $P\left(\left|X_n-X\right|>\epsilon \right)\le P\left(\left|X_n-X\right|>{\epsilon }_n\right)$ ，有

$\begin{array}{c}{\displaystyle \sum _{n=1}^{\infty }P\left(\left|X_n-X\right|>\epsilon \right)}\le {\displaystyle \sum _{n=1}^{N}P\left(\left|X_n-X\right|>\epsilon \right)}+{\displaystyle \sum _{n=N+1}^{\infty }P\left(\left|X_n-X\right|>{\epsilon }_n\right)}\\ \le {\displaystyle \sum _{n=1}^{N}P\left(\left|X_n-X\right|>\epsilon \right)}+{\displaystyle \sum _{n=1}^{\infty }P\left(\left|X_n-X\right|>{\epsilon }_n\right)}<\infty \end{array}$

得 $X_n\stackrel{\text{c}\text{.c}\text{.}}{\to }X$ 。

“⟹”：若 $X_n\stackrel{\text{c}\text{.c}\text{.}}{\to }X$ ，取实数序列 $\left\{{\eta }_n\right\}$ ， ${\eta }_n\downarrow 0$ ，则对 ${\eta }_1>0$ ，有

$M_1={\displaystyle \sum _{n=1}^{\infty }P\left(\left|X_n-X\right|>{\eta }_1\right)}<\infty$

又因为

${\displaystyle \sum _{n=1}^{\infty }P\left(\left|X_n-X\right|>{\eta }_2\right)}<\infty$

所以存在正整数 $N_1$ ，使得

${\displaystyle \sum _{n=N_1+1}^{\infty }P\left(\left|X_n-X\right|>{\eta }_2\right)}<\frac{1}{2^2}$

所以有

${\displaystyle \sum _{n=1}^{N_1}P\left(\left|X_n-X\right|>{\eta }_1\right)}+{\displaystyle \sum _{n=N_1+1}^{\infty }P\left(\left|X_n-X\right|>{\eta }_2\right)}<M_1+\frac{1}{2^2}$

同理，对 ${\eta }_k>0$ ，存在正整数 $N_{k-1}$ ，使得

${\displaystyle \sum _{n=N_{k-1}+1}^{\infty }P\left(\left|X_n-X\right|>{\eta }_k\right)}<\frac{1}{k^2}$

对 ${\eta }_{k+1}>0$ ，存在正整数 $N_k$ ，且满足 $N_{k-1}+1\le N_k$ ，使得

${\displaystyle \sum _{n=N_k+1}^{\infty }P\left(\left|X_n-X\right|>{\eta }_{k+1}\right)}<\frac{1}{{\left(k+1\right)}^2}$

所以

${\displaystyle \sum _{n=N_{k-1}+1}^{N_k}P\left(\left|X_n-X\right|>{\eta }_k\right)}\le {\displaystyle \sum _{n=N_{k-1}+1}^{\infty }P\left(\left|X_n-X\right|>{\eta }_k\right)}<\frac{1}{k^2}$

令 $N_0=0$ ，有

${\displaystyle \sum _{k=1}^{\infty }{\displaystyle \sum _{n=N_{k-1}+1}^{N_k}P\left(\left|X_n-X\right|>{\eta }_k\right)}}<M_1+{\displaystyle \sum _{k=1}^{\infty }\frac{1}{k^2}}<\infty$

对每个 $k\ge 1$ ，当 $N_{k-1}+1\le n\le N_k$ 时，取这些 ${\epsilon }_n={\eta }_k$ 。由此得 ${\epsilon }_n\downarrow 0$ ，而且满足

${\displaystyle \sum _{n=1}^{\infty }P\left(\left|X_n-X\right|>{\epsilon }_n\right)}={\displaystyle \sum _{k=1}^{\infty }{\displaystyle \sum _{n=N_{k-1}+1}^{N_k}P\left(\left|X_n-X\right|>{\eta }_k\right)}}<M_1+{\displaystyle \sum _{k=1}^{\infty }\frac{1}{k^2}}<\infty$ 。 □

由Borel-Cantelli引理知 $X_n\stackrel{\text{c}\text{.c}\text{.}}{\to }X\Rightarrow X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X$ ，但 $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X\cancel{\Rightarrow }{X}_n\stackrel{\text{c}\text{.c}\text{.}}{\to }X$ ，如下例。

例3.1 设 $\xi ,{\xi }_1,{\xi }_2,\cdots$ 是独立同分布的随机变量序列， $\xi$ 服从双边Pareto分布，其密度函数为

$f\left(x\right)=\{\begin{array}{l}{\left|x\right|}^{-3},当\left|x\right|>1\\ 0,其它\end{array}$

则 $E\left|\xi \right|=2<\infty$ ， $E\left(\xi \right)=0$ ， $E\left({\xi }^2\right)=\infty$ 。令 $X_n=\frac{{\xi }_1+{\xi }_2\cdots +{\xi }_n}{n}$ ，由Kolmogorov强大数定律( [1] , p. 295)， $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }0\iff E\left|\xi \right|<\infty$ 且 $E\left(\xi \right)=0$ ；由Hsu-Robbins-Erdos强大数定律( [1] ，p312)， $X_n\stackrel{\text{c}\text{.c}\text{.}}{\to }0\iff E\left({\xi }^2\right)<\infty$ 且 $E\left(\xi \right)=0$ 。由此知 $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }0$ ，但不成立。

由(5)式知 $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X\Rightarrow X_n\stackrel{p}{\to }X$ ，但 $X_n\stackrel{p}{\to }X\cancel{\Rightarrow }{X}_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X$ ，如下面的例子。

例3.2 令随机变量 $X_n$ 的分布为 $P\left(X_n=0\right)=1-\frac{1}{n}$ ， $P\left(X_n=1\right)=\frac{1}{n}$ ，则对 $0<\epsilon <1$ ，有 $P\left(\left|X_n-0\right|>\epsilon \right)=P\left(X_n=1\right)=\frac{1}{n}\to 0$ 当 $n\to \infty$ ，得 $X_n\stackrel{p}{\to }0$ 。然而当随机变量序列 $X_1,X_2,\cdots$ 相互独立时，对任意 $0<\epsilon <1$ ，

${\displaystyle \sum _{n=1}^{\infty }P\left(\left|X_n-0\right|>\epsilon \right)}={\displaystyle \sum _{n=1}^{\infty }P\left(X_n=1\right)}={\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^2}}=\infty$

由Borel-Cantelli引理知 $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }0$ 不成立。

下面的命题3.2和3.3是两个很强的条件。

命题3.2 设有随机变量序列 $X_1,X_2,\cdots$ 及随机变量X，若

$\exists {\epsilon }_k\downarrow 0,\text{s}\text{.t}\text{.}P\left(\left|X_n-X\right|>{\epsilon }_k\right)=0,\text{for}\text{all}{\epsilon }_k$ (15)

则。简记为 $X_n\stackrel{\text{a}\text{.s}.}{=}X,\forall n$ 。

证 因

$\begin{array}{c}P\left(X_n\ne X\right)=P\left(\left|X_n-X\right|\ne 0\right)\\ =P\left({\displaystyle \underset{k=1}{\overset{\infty }{\cup }}\left\{\left|X_n-X\right|>{\epsilon }_k\right\}}\right)\\ \le {\displaystyle \sum _{k=1}^{\infty }P\left(\left|X_n-X\right|>{\epsilon }_k\right)=0}\end{array}$

所以

$P\left(X_n=X\right)=1-P\left(X_n\ne X\right)=1-0=1$ . □

易知(15)式⟺ $X_n\stackrel{\text{a}\text{.s}.}{=}X,\forall n$ ，因从右推出左是显然的。

若对任意n，下式成立

$\exists {\epsilon }_n\downarrow 0,\text{s}\text{.t}\text{.}P\left(\left|X_n-X\right|>{\epsilon }_n\right)=0$ (16)

则容易知道(16)式比(15)式给的条件稍弱，因 $k\ge n$ 时， ${\epsilon }_k\le {\epsilon }_n$ ，所以(15)式⟹(16)式。然而(16)式⇏(15)式，如下面的例3.3。

例3.3 令随机变量 $X_n$ 的分布为 $P\left(X_n=0\right)=1-\frac{1}{n}$ ， $P\left(X_n=\frac{1}{n}\right)=\frac{1}{n}$ 。令，正实数序列 ${\epsilon }_1,{\epsilon }_2,\cdots$ 取为 ${\epsilon }_n=\frac{2}{n}$ ，则有(16)式成立。但对任意的正实数序列 ${{\epsilon }^{\prime }}_1,{{\epsilon }^{\prime }}_2,\cdots$ 单调递减以0为极限，知当 ${{\epsilon }^{\prime }}_k\ge \frac{1}{n}$ 时， $P\left(\left|X_n-0\right|>{{\epsilon }^{\prime }}_k\right)=0$ ；当 ${{\epsilon }^{\prime }}_k<\frac{1}{n}$ 时， $P\left(\left|X_n-0\right|>{{\epsilon }^{\prime }}_k\right)=P\left(X_n=\frac{1}{n}\right)=\frac{1}{n}>0$ 。对任意给定n必有某些 ${{\epsilon }^{\prime }}_k<\frac{1}{n}$ ，所以(15)式不成立。

上面直接由 $X_n$ 的分布容易得到 $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }0$ ，因对样本空间中任意 $\omega$ ，有 ${\lim }_{n\to \infty }{X}_n\left(\omega \right)=0$ ，所以 $P\left({\lim }_{n\to \infty }{X}_n\left(\omega \right)=0\right)=1$ 。

下面命题说明(16)式比完全收敛的条件更强。

命题3.3 设有随机变量序列 $X_1,X_2,\cdots$ 及随机变量X，若(16)式成立，则(3)式成立。

证 因存在使(16)式成立的数列 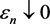$\left\{{\epsilon }_n\right\}$ ，，所以对任意 $\epsilon >0$ ，必存在N，当 $n>N$ 时， ${\epsilon }_n<\epsilon$ ，由此得到

$\begin{array}{c}{\displaystyle \sum _{n=1}^{\infty }P\left(\left|X_n-X\right|>\epsilon \right)}\le {\displaystyle \sum _{n=1}^{N}P\left(\left|X_n-X\right|>\epsilon \right)}+{\displaystyle \sum _{n=N+1}^{\infty }P\left(\left|X_n-X\right|>{\epsilon }_n\right)}\\ ={\displaystyle \sum _{n=1}^{N}P\left(\left|X_n-X\right|>\epsilon \right)}+0<\infty \end{array}$

得(3)式成立。 $\square$

由命题3.3知，(16)式成立可得(3)式成立，从而 $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X$ 。不过也很容易地由(16)式直接得到 $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X$ 。因对任意 $\epsilon >0$ ，存在N，使得当 $m>N$ 时， ${\epsilon }_m<\epsilon$ ，所以当 $n>N$ 时

$P\left({\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>\epsilon \right\}}\right)\le {\displaystyle \sum _{m=n}^{\infty }P\left(\left|X_m-X\right|>\epsilon \right)}\le {\displaystyle \sum _{m=n}^{\infty }P\left(\left|X_m-X\right|>{\epsilon }_m\right)}=0$

从而

$\underset{n\to \infty }{\lim }P\left({\displaystyle \underset{m=n}{\overset{\infty }{\cup }}\left\{\left|X_m-X\right|>\epsilon \right\}}\right)=0$

得(5)式成立，所以有 $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X$ 。

由命题3.3知，(16)式⟹(3)式，但(3)式⇏(16)式，如下面的例3.4。

例3.4 设有随机变量序列 $X_1,X_2,\cdots$ ，其中 $X_n$ 的分布律为

$P\left(X_n=0\right)=1-\frac{1}{n^2},P\left(X_n=1\right)=\frac{1}{n^2}$

则对任意 $0<\epsilon <1$ ，有

${\displaystyle \sum _{n=1}^{\infty }P\left(\left|X_n-0\right|>\epsilon \right)}={\displaystyle \sum _{n=1}^{\infty }P\left(X_n=1\right)}={\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^2}}<\infty$

所以(3)式成立。然而对任意的正实数序列 ${\epsilon }_1,{\epsilon }_2,\cdots$ 单调递减以0为极限，存在N，当 $n>N$ 时， ${\epsilon }_n<1$ 。所以当 $n>N$ 时， $P\left(\left|X_n-0\right|>{\epsilon }_n\right)=P\left(X_n=1\right)=\frac{1}{n^2}>0$ 。由此得(16)式不成立。

由以上命题，有如下结论

$X_n\stackrel{\text{a}\text{.s}.}{=}X$ ⟺(15)⇒(16)⇒(14)⟺ $X_n\stackrel{\text{c}\text{.c}}{\to }X$ ⇒ $X_n\stackrel{\text{a}\text{.s}\text{.}}{\to }X$ ⟺(12)⇒ $X_n\stackrel{p}{\to }X$

而且举例说明了上面蕴含关系的相反方向不成立。

文章引用

袁代林. 随机变量序列完全收敛的等价及充分条件
Equivalent and Sufficient Conditions of Complete Convergence of Random Variables Sequence[J]. 应用数学进展, 2018, 07(06): 673-679. https://doi.org/10.12677/AAM.2018.76080

参考文献