Advances in Applied Mathematics
Vol.
07
No.
09
(
2018
), Article ID:
26709
,
6
pages
10.12677/AAM.2018.79133
The Representation of the Generalized Inverse of a Hamilton Matrix
Yu Guo*, Zeyuan Li, Xiaotong Liu, Wenhui He
School of Mathematical Science, Inner Mongolia University, Hohhot Inner Mongolia

Received: Aug. 15th, 2018; accepted: Aug. 30th, 2018; published: Sep. 6th, 2018

ABSTRACT
The aim of this paper is to establish an explicit representation of the Drazin inverse of a Hamilton matrix
under certain conditions. Then we give a formula for the Drazin inverse of a Hamilton matrix 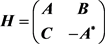 when the generalized Schur complement
.
when the generalized Schur complement
.
Keywords:Hamilton Matrix, Generalized Inverse, Drazin Inverse, Schur Complement

Hamilton矩阵广义逆的表示
郭宇*,李泽塬,刘晓彤,贺文慧
内蒙古大学,数学科学学院,内蒙古 呼和浩特
收稿日期:2018年8月15日;录用日期:2018年8月30日;发布日期:2018年9月6日

摘 要
本文首先给出了Hamilton矩阵
在一定条件下Drazin逆 的表达式,其次给出了当广义Schur补
时Drazin逆
的表达式。
的表达式,其次给出了当广义Schur补
时Drazin逆
的表达式。
关键词 :Hamilton矩阵,广义逆,Drazin逆,Schur补

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Hamilton体系是由19世纪爱尔兰数学家兼物理学家W. R. Hamilton从几何光学着手创建起来的理论模式,而后他将此模式创造性的应用于经典力学,得到了在经典力学范畴内的又一种力学描述形式—Hamilton力学 [1]。作为Hamilton系统中最简单且最基本的形式,有限维线性Hamilton系统所对应的系数矩阵如下:
,
其中 是Hermite矩阵, 是A的共轭转置,此时称H是Hamilton矩阵 [2]。Hamilton矩阵作为一种特殊的分块矩阵,在数学以及力学的很多方面都有重要的作用,如谱的计算、Riccati方程的解以及相关的不变子空间刻画等 [3]。
设矩阵 ,A的Drazin逆是满足以下条件的唯一复矩阵 :
, , ,
其中k是使得 成立的最小非负整数,记 为A的指标 [4]。当 时,则称 为A的群逆。如果A是非奇异的,则 且 ,本文中令 。
Drazin逆在Markov链、奇异微分方程和差分方程、迭代方法等各领域起着重要作用 [5]。本文主要研究了Hamilton矩阵在一定条件下的Drazin逆,并给出了一些 的表达式。
2. 引理
为了得到本文的主要结论,首先给出以下引理。
引理1 ( [6]). 令 ,如果 ,那么 。
引理2 ( [6]). 令 ,如果 ,那么 。
引理3 ( [7]). 令 ,如果 ,则 。
引理4 ( [8]). 令 ,如果 ,P是l-幂零的,则 。
如果 ,Q是s-幂零的,则
.
引理5 ( [9]). 令 , , 。若 , , ,则
, .
3. 主要结论及证明
定理1. 令 ,其中A为方阵,如果 , , , ,那么
.
证明:将矩阵H分解,得
,
令
, ,
通过条件我们得到
 ,
,
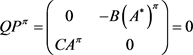 ,
,
因此,矩阵P和Q满足引理2,得到
定理2. 令 ,其中A为方阵,如果 , , , ,那么
.
证明:将矩阵H分解,得
,
令
, ,
通过引理3,我们可以得到
, .
通过条件得
,
,
因此,矩阵P和Q满足引理2,得到
定理3. 令
,其中A为方阵,如果
,  ,
,
,那么
,
,
,那么
.
证明:将矩阵H分解,得
,
令
, ,
通过条件我们得到
,
,
因此,矩阵P和Q满足引理1,得到
下面我们给出A在矩阵H的广义Schur补 时 的表达式。
定理4. 令 ,其中A为方阵,如果 , , , ,那么
,
其中
,
,
.
证明:由 可得
,
令
, ,
通过条件可得 , , 。由引理,我们得到
, (1)
接下来我们求 。
我们将Q分解为 ,其中
, ,
可以得到 是 阶幂零的, ,并且 ,由引理4可得
,
其中 。
下面求 ,由引理5,
 ,
,
,
,
再由 ,可以得到
, ,
令 , ,则
,
将 代入(1),证毕。
基金项目
内蒙古大学校级大学生创新创业训练计划项目(项目编号:201711198)。
文章引用
郭宇,李泽塬,刘晓彤,贺文慧. Hamilton矩阵广义逆的表示
The Representation of the Generalized Inverse of a Hamilton Matrix[J]. 应用数学进展, 2018, 07(09): 1147-1152. https://doi.org/10.12677/AAM.2018.79133
参考文献
- 1. 冯康. 哈密尔顿系统的辛几何算法[M]. 杭州: 浙江科技出版社, 2003.
- 2. 吴德玉, 阿拉坦仓. 分块算子矩阵谱理论及其应用[M]. 北京: 科学出版社, 2013.
- 3. 邢立刚. 一类无穷维Hamilton算子谱的刻画[M]. 呼和浩特: 内蒙古大学出版社, 2007.
- 4. Drzain, M.P. (1958) Pseudo-Inverses in Associative Rings and Semigroups. The American Mathematical Monthly, 65, 506-514. https://doi.org/10.1080/00029890.1958.11991949
- 5. Bru, R., Climent, J.J. and Neumann, M. (1995) On the Index of Block Upper Triangular Matrices. SIAM Journal on Matrix Analysis and Applications, 16, 436-447. https://doi.org/10.1137/S0895479892235587
- 6. Xia, L. and Deng, B. (2017) The Drazin Inverse of the Sum of Two Matrices and Its Applications. Filomat, 31, 5151-5158. https://doi.org/10.2298/FIL1716151X
- 7. Catral, M., Olesky, D.D. and Van Den Driessche, P. (2009) Block Representations of the Drazin Inverse of a Bipartite Matrix. The Electronic Journal of Linear Algebra, 18, 98-107. https://doi.org/10.13001/1081-3810.1297
- 8. Hartwig, R.E., Wang, G. and Wei, Y.M. (2001) Some Additive Results on Drazin Inverse. Linear Algebra and Its Applications, 322, 207-217. https://doi.org/10.1016/S0024-3795(00)00257-3
- 9. Miao, J. (1989) Results of Drazin Inverse of a 2 × 2 Block Matrices. Journal of Shanghai Normal University, 18, 25-31.
NOTES
*通讯作者。