Advances in Applied Mathematics
Vol.
07
No.
11
(
2018
), Article ID:
27626
,
9
pages
10.12677/AAM.2018.711162
Study on the Formation Mechanism of Corruption and the Mechanism of Reward and Punishment
Xueli Chen, Jicheng Hou
Beijing University of Information Technology, Beijing
Received: Oct. 23rd, 2018; accepted: Nov. 13th, 2018; published: Nov. 20th, 2018

ABSTRACT
Corruption has always been the object of attention and research in many countries. Like other countries, China has been doing its part in preventing and punishing corruption. Severe penalties, such as the death penalty, have even been promulgated, but there’s still no effective control of corruption, so we have to rethink what kind of mechanism we can put in place to better reduce or even eliminate corruption. This paper starts from a new way of thinking; a four-party evolutionary game model, including corruption, investigation and punishment, third party intervention mechanism and public opinion supervision, is established by using evolutionary games. By analyzing the game model, this paper provides a valuable reference for the improvement of the mechanism of prevention and punishment of corruption.
Keywords:Corruption, Evolutionary Game, Replication Dynamics
腐败现象形成机理与奖惩机制研究
陈雪莉,侯吉成
北京信息科技大学,北京
收稿日期:2018年10月23日;录用日期:2018年11月13日;发布日期:2018年11月20日

摘 要
腐败问题一直是很多国家关注和研究的对象,同其他国家一样,中国在预防腐败和惩罚腐败上也一直很尽职尽责,甚至还颁布了诸如死刑等严厉的刑罚,但是仍然没有让腐败现象得到很好的控制。这让我们不得不重新思考到底建立什么样的机制才能更好地减少甚至杜绝腐败现象。本文从一个全新的思路出发,使用演化博弈的方法建立一个腐败–查处–第三方干预机制–舆论监督的四方演化博弈模型,通过对博弈模型的分析,为腐败的预防与惩罚机制的完善提供有价值的参考。
关键词 :腐败,演化博弈,复制动态

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
腐败问题一直是社会科学研究的热点之一,它通常被定义为“利用职务便利谋取私利” [1] ,在现实中不论是多大职位的官员都有可能腐败,因为腐败往往意味着轻而易举获得巨大的经济收入,而人的有限理性在面对金钱诱惑时往往会十分脆弱。腐败问题对一个国家的影响是巨大的,它直接关系到一个国家的经济以及各方面发展和人民民众的根本利益,所以我国一直都很重视反腐工作。近些年学者们大都使用完全信息静态博弈思想研究腐败问题,但是现实中完全理性的人根本不可能存在,因此在腐败问题的分析上有很大的局限性。本文采用演化博弈的方法分析腐败问题,这对腐败问题的研究或许是一个新的出发点和突破口。
在本文中我们规定博弈方分别为下级官员、上级官员,第三方干预(比上下级官员权利更大的国家监察机关)和新媒体普通民众等舆论监督。为了便于分析,本文暂不考虑腐败现象中的行贿者。采用的方法:1) 分析下级官员腐败的原因和影响各博弈方策略选择的要素;2) 构建博弈得益矩阵;3) 根据得益矩阵分别求出复制动态;4) 对博弈复制动态方程进行稳定性分析;5) 提出防治腐败的对策和建议。
2. 腐败现象四方演化博弈模型构建
自我国进入新时代以来,腐败行为不再单单依赖于国家官员和监察机关等公务部门调查处理,有许多的腐败受贿案件也是通过网络媒体和普通民众的举报传播引起相关机构的重视进而进行调查从而得以查处。
2.1. 模型假设
假设1:博弈方为有差别(各博弈方)的有限理性群体:参与者1是下级官员,参与者2是上级官员,参与者3是监察机关参与者4是舆论监督,他们的策略集合分别为{不腐败,腐败},{查处,不查处},{监察,不监察},{举报,不举报}。
假设2: , (具体根据腐败金额而定),其中各个参数值符号及其对应含义如表1所示。
假设3:监察机关监察上、下级官员所需成本以及上级官员成功查处腐败后所获额外收益均从下级官员腐败所获额外收益和腐败罚金中补偿,除此之外若腐败金额还有剩余则收归监察机关。
假设4:博弈模型中,若上级官员选择查处腐败策略,则舆论监督的影响可忽略不计。
Table 1. Symbols of parameters and their meanings
表1. 各参数符号及其含义
2.2. 演化博弈收益矩阵
因每位参与主体均有两个策略组合,所以理论上可形成 种博弈策略组合,具体见表2。
Table 2. The income Matrix of asymmetric Evolutionary Game on Corruption
表2. 腐败问题非对称演化博弈收益矩阵
2.3. 复制动态方程求解
假设博弈初始阶段,在下级官员群体中,采取{不腐败}策略的下级官员所占群体比例为x,则采取{腐败}策略的比例为 ;在上级官员群体中,采取{查处}策略的上级领导所占群体比例为y,则采取{不查处}策略的比例为 ;在第三方监察官员群体中,采取{监察}策略的群体所占群体比例为z,则采取{不监察}策略的比例为 ;在第四方舆论监督群体中,采取{举报}策略所占群体比例为 ,采取{不举报}策略所占群体比例为 ,其中 [2] 。
现假设在两个博弈群体中,所有博弈方群体成员均采用纯策略,即在策略集合中选取唯一确定的策略。令M是某一博弈群体中所有纯策略组合的集合,定义 博弈群体中所有在 时刻采用纯策略 的成员集合,变量 为在t阶段采用纯策略 的成员群体比例,则可得:
(1)
在t阶段采用纯策略 的期望收益为:
(2)
其中 表示采用纯策略 的博弈方在另一类博弈方成员采用纯策略 时的期望收益,可知群体的平均期望收益为:
(3)
在博弈中有限理性的博弈方会根据直觉和判断力发现不同策略的得益差异,得益较差类型的博弈方或迟或早都会发现改变策略对自己更有利,进而开始模仿其他类型的博弈方,所以博弈中几种类型博弈方的比例是随时间变化的,是时间t的函数,而比例动态变化的速度往往取决于博弈方学习模仿的速度。通常情况下,博弈方学习模仿的速度取决于两个因素,一是模仿对象的数量大小;二是模仿对象的成功程度(可用模仿对象策略得益表示)。从而提出下面这样的连续时间复制动态模型
,( )为常数 (4)
对(1)求导可得:
(5)
将(1),(4)代入(5)化简可得:
(6)
下面分别计算本文四方博弈群体的复制动态方程并进行分析。
2.3.1. 下级官员复制动态分析
下级官员选择“不腐败”和“腐败”策略的期望收益分别用 表示:
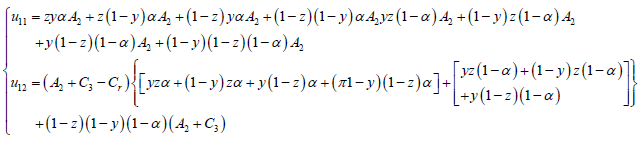 (7)
(7)
化简得:
(8)
下级官员的平均期望得益为:
(9)
将(8)代入(9)中可得:
(10)
由此得到下级官员的复制动态方程为;
(11)
方程(11)的含义是,选择“不腐败”策略的下级官员的比例随时间的变化率 与x成正比,与选择“不腐败”时下级官员期望收益大于平均收益的幅度 也成正比 [3] 。
2.3.2. 上级官员复制动态分析
上级官员的‘查处’和‘不查处’策略的期望收益分别用 表示:
(12)
化简得:
(13)
上级官员的平均期望得益为:
(14)
将(13)代入(14)中得:
(15)
所以上级官员的复制动态方程为:
(16)
方程(16)的含义是选择“查处”策略的上级关于的比例随时间的变化率 与y成正比,也与选择“查处”时期望收益大于平均收益的幅度 成正比。
2.3.3. 监察机关复制动态分析
第三方干预“监察”和“不监察”策略的期望收益分别用 表示:
(17)
化简得:
(18)
第三方干预的平均期望得益为:
(19)
将(18)代入(19)中得:
(20)
所以第三方干预的复制动态方程为:
(21)
方程(21)的含义是选择“监察”策略的第三方干预的比例随时间的变化率 与z成正比,也与选择“监察”时期望收益大于平均收益的幅度 成正比。
2.3.4. 舆论监督复制动态方程
舆论监督“举报”和“不举报”的期望收益分别用 表示:
(22)
化简得:
(23)
舆论监督的平均期望得益为:
(24)
将(23)代入(24)中得:
(25)
所以第四方舆论监督的复制动态方程为:
(26)
方程(26)的含义是选择“举报”策略的第四方舆论监督的比例随时间的变化率 与 成正比,也与选择“举报”时期望收益大于平均收益的幅度 成正比。
2.4. 复制动态稳定性分析
复制动态的稳定状态,即在复制动态过程中采用两种策略博弈方比例不变的水平。在这种均衡状态下,任何一个参与者偏离均衡都将是无利可图的,所以参与博弈者都不会想单独改变策略。在数学上,相当于当干扰使x出现低于 时, 必须大于0,当干扰使x出现高于 时, 必须小于0,也就是说在这些稳定状态处 的导数 必须小于0,即 ,这便是微分方程的“稳定性定理” [4] 接下来分别求解博弈中四个群体的稳定状态并分析。
2.4.1. 下级官员稳定性分析
由(11)计算可知:若
,有
,即此时所有x都为稳定状态;若
,令
得
为
的两个稳定状态 [5] ;由于
,有下面两种情况:由
知,
时,
,
,故
为平衡点,
不是平衡点,此时下级官员的复制动态会趋向于稳定状态
即博弈方采用“不腐败”策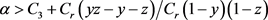 时,有
,
,故
为平衡点,
不是平衡点,此时下级官员的复制动态会趋向于稳定状态
,即博弈方采用“腐败”策略。
时,有
,
,故
为平衡点,
不是平衡点,此时下级官员的复制动态会趋向于稳定状态
,即博弈方采用“腐败”策略。
2.4.2. 上级官员稳定性分析
首先根据
找出上级官员的稳定状态,由(16)计算可知,若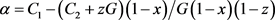 ,有
,即此时所有y都为稳定状态;若
,令
得
为y的两个稳定状态;由于
,有以下两种情况:由
知:
,有
,即此时所有y都为稳定状态;若
,令
得
为y的两个稳定状态;由于
,有以下两种情况:由
知:
时, , ,此时 为平衡点, 不是平衡点,上级官员的复制动态会趋向于 ,即博弈方都采用“查处”策略; 时 , ,此时 为平衡点, 不是平衡点,上级官员的复制动态会趋向于 ,即博弈方都采用“不查处”策略。
2.4.3. 监察机关稳定性分析
由(21)计算可知:若
时,有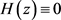 ,即此时所有z都为稳定状态;
,即此时所有z都为稳定状态;
若 ,令 得 为z的两个稳定状态;由于 , ,有以下两种情况: 时,有 ,此时 为平衡点, 不是平衡点,监察官员的复制动态会趋向于 ,即博弈方都采用“监察”策略; 时,有 ,此时 为平衡点, 不是平衡点,监察官员的复制动态会趋向于 ,即博弈方都采用“不监察”策略。
2.4.4. 舆论监督稳定性分析
由(26)可知:若
时,有
,此时所有
都为稳定状态;若
,令
得
为
的两个稳定状态;由于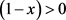 ,
,有以下两种情况:
时,有
,此时
为平衡点,
不是平衡点,舆论监督群体的复制动态会趋向
,即博弈方采用“举报”策略;
时,有
此时
为平衡点,
不是平衡点,监察官员的复制动态会趋向于
,博弈方采用“不举报”策略。
,
,有以下两种情况:
时,有
,此时
为平衡点,
不是平衡点,舆论监督群体的复制动态会趋向
,即博弈方采用“举报”策略;
时,有
此时
为平衡点,
不是平衡点,监察官员的复制动态会趋向于
,博弈方采用“不举报”策略。
2.5. 四方博弈复制动态均衡解分析
综合博弈中四个群体各自复制动态分析 [6] 可得均衡解如表3。
Table 3. Equilibrium solution of tetragonal game
表3. 四方博弈均衡解
表3中有:
分析可知,当下级官员腐败受贿金额 增加时,对其腐败的罚金 也应同样增加,如此才能有效减少下级官员选择“腐败”策略,使其逐渐趋向于选择“不腐败”策略,而具体该以怎样的比例增加,需要根据不同地区的经济政策和发展情况制定实施。对于上级官员来说查处腐败所需成本 的大小直接影响其策略选择,如果个别腐败现象查处成本 较大,现实生活中上级官员便有极大可能不采取任何调查举措,这便会导致腐败行为者更加猖狂。随着上级官员选择“不查处”策略群体比例的增加,监察机关增大对其不作为的经济处罚 ,同时如果能增加其成功查处腐败后所获经济奖赏或者政治褒奖 都能有效促使更多的上级官员趋向于选择“查处”策略,所以赏罚结合才能更有效的督促官员们更多地为人民服务,更多的履行自己的职责,减少腐败现象。
对第三方监察机关来说,国家增加其监察不力的惩罚 ,才会使其更加尽职尽责,更好的监察上、下级官员,减少社会上腐败案件和包庇腐败现象的循环发生。第四方舆论监督泛指如今网络新媒体报道以及民众匿名举报等一系列普通民众监督,分析可知只有当举报腐败后所获收益 大于自身举报所需成本 时,民众们才会更多地趋向于选择“举报”策略,这也是有限理性下大部分普通人的正常心理。因此有关负责部门面对普通民众的匿名举报时应更加重视,如果举报有实,应给与物质精神或者经济方面的丰富奖励,从而鼓励其更多地监督身边各种贪污腐败行为,进而形成社会上良好的政治风气。同样网络新媒体等途径举报受贿腐败也是现如今很有影响力的一个举措,毕竟现在是一个网络发达的时代,通过网络民众能更好地关注到一些平常接触不到的事情,对新媒体报道来说成功举报腐败行贿现象会使其阅读量、点击量和关注度都能得到很大的提高,这对他们来说也是获取经济效益的一个有效途径。所以监察机关或者其他政府部门面对民众举报时,应正确看待调查,不能全然采取不重视或者不闻不问的态度。
3. 结论
腐败问题一直是国家和人民共同关心的问题,本文构建四方博弈分析如何能有效减少腐败现象,针对不同博弈方群体分别给出了一些意见建议,而在现实生活中更要从思想道德建设方面入手,加强对基层官员和领导的自身素质教育,加强普通民众对腐败现象危害性的认知,让全民参与监督腐败,建立更完善更严苛的奖罚体制,对清廉洁身自好的官员予以奖励和荣誉,对不为人民服务选择腐败的官员给予严厉的惩罚,从多方面着手以期实现零腐败目标,具体给出几个建议:
1) 提高上级领导查处腐败现象后所得收益 ,这里多指经济效益,如此上级领导会更乐于对腐败现象进行查处,理性的下级官员更不会冒着更高的被查处风险选择腐败,这也侧面说明了“高薪养廉” [7] 思想的重要性,关于这方面可借鉴其他国家做法。
2) 加重对下级官员腐败行为的经济处罚 [8] ,这样腐败者才会因为影响到自身实际利益而有所收敛,所以应完善相关法律法规,寻找摸索最符合自身国情的有效措施。
3) 提高对上级官员不查处腐败的经济惩处 ,现实中存在不少官官相护、上级官员包庇下级官员腐败甚至伙同参与腐败等一系列不正风气,所以需完善监察政策 [9] ,不单单要惩处下级官员,对待不认真查处腐败现象的上级官员更要给予严厉的惩罚,让官员们感觉到时刻身处监督中而不敢也不能腐败。
致谢
本篇论文是在我的导师侯吉成教授精心指导和悉心关怀下完成的。在文章写作过程中,侯老师对我的极大支持和鼓励,对文章出了很多宝贵的意见与建议,给了我最大的帮助。在此向侯吉成老师致以崇高的敬意和衷心的感谢!
文章引用
陈雪莉,侯吉成. 腐败现象形成机理与奖惩机制研究
Study on the Formation Mechanism of Corruption and the Mechanism of Reward and Punishment[J]. 应用数学进展, 2018, 07(11): 1393-1401. https://doi.org/10.12677/AAM.2018.711162
参考文献
- 1. 朱江南, 王燕燕. 严刑能遏制腐败吗?——以中国为例的博弈论分析[J]. 经济社会体制比较, 2013(2): 145-153.
- 2. 宋余超. 网络舆情形成阶段主体博弈模型研究[D]: [硕士学位论文]. 福州: 福州大学, 2016.
- 3. 俞建. 博弈论选讲[M]. 北京: 科学出版社, 2014: 47-60.
- 4. 谢识予. 经济博弈论(第三版) [M]. 上海: 复旦大学出版社, 2012: 210-246.
- 5. 徐建中, 徐莹莹. 基于演化博弈的制造企业低碳技术采纳决策机制研究[J]. 运筹与管理, 2014(5): 264-272.
- 6. Dieckmann, U. and Law, R. (1996) The Dynamical Theory of Coevolution: A Derivation from Stochastic Ecological Processes. Journal of Mathematical Biology, 34, 579-612. https://doi.org/10.1007/BF02409751
- 7. 李芳. 成本与收益理论在预防贿赂犯罪中的应用研究[D]: [硕士学位论文]. 长沙: 湖南大学, 2010: 1-3.
- 8. 金明军. 我国基层干部腐败防治问题研究[D]: [硕士学位论文]. 大庆: 东北石油大学, 2016: 28-33.
- 9. 易刚强. 基于演化博弈理论的公职人员腐败及监督方反腐败的行为选择机理研究[D]: [硕士学位论文]. 成都: 西南财经大学, 2014.
