Advances in Applied Mathematics
Vol.
09
No.
02
(
2020
), Article ID:
34191
,
6
pages
10.12677/AAM.2020.92019
Division of Landslide Stages Based on DBSCAN Algorithm
Jingyun Lu, Wenqiang Luo, Yan Li
School of Mathematics and Physics, China University of Geosciences, Wuhan Hubei

Received: Jan. 25th, 2020; accepted: Feb. 7th, 2020; published: Feb. 14th, 2020

ABSTRACT
The division of landslide stages is an important issue in the evolution of landslides. The Density-Based Spatial Clustering of Applications with Noise (DBSCAN) algorithm is used to cluster the cumulative displacement sequence data of the landslide in this paper. When the number of clustering clusters is greater than the number of stages, a statistic M is introduced to indicate the degree of the landslide changing from a stable development state to an unstable rapid deformation development state. The landslide moment corresponding to the smallest statistical value m is selected as the stage division point of landslide evolution and deformation. The experimental results show that it agrees with the boundary point of the actual landslide stage. It is shown that the DBSCAN algorithm can effectively divide the landslide stage accurately.
Keywords:DBSCAN Algorithm, Statistics M, Stage Division, Landslide

基于DBSCAN算法的滑坡阶段划分
卢静云,罗文强,李燕
中国地质大学数学与物理学院,湖北 武汉

收稿日期:2020年1月25日;录用日期:2020年2月7日;发布日期:2020年2月14日

摘 要
滑坡的阶段划分是滑坡演化过程中的一个重要问题。在本文中,利用DBSCAN算法对滑坡的累积位移序列数据进行聚类,在聚类簇的个数大于阶段数情况下,引入一个统计量M表示滑坡从稳定发育状态变化为不稳定的快速变形发育状态的程度。选择最小的统计值m所对应的滑坡时刻为滑坡演化变形的阶段划分点。实验结果显示,与实际的滑坡阶段分界点吻合,表明DBSCAN算法能有效的对滑坡阶段进行准确的划分。
关键词 :DBSCAN算法,统计量M,阶段划分,滑坡

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
滑坡的阶段划分是滑坡演化过程中的一个重要问题。找到合适的指标检测滑坡进入失稳破环的状态,即滑坡演化发育的后期阶段,对滑坡的预警预报具有重要理论和现实意义。
罗文强,李飞翱等 [1] 提出了多元时间序列分析的滑坡演化阶段划分,建立多因素的时间序列预测模型并利用Chow分割点检验(Chow Breakpoint Test),将滑坡划分为3个阶段。黄丽等 [2] 提出了基于有序样品聚类最优二分割算法的滑坡演化阶段划分,利用有序样品聚类的最优二分割算法对滑坡演化阶段进行划分。
文献 [1] 中的Chow分割点检验实质上是分割成2个以上子集,计算整体与子集的相对变化程度,寻找最优分割子集的计算量较为复杂。文献 [2] 中的分割算法计算局部的最优分割点,存在主观判断的问题。利用机器学习算法研究滑坡的演化过程是目前较广泛的一个发展方向。DBSCAN (Density-Based Spatial Clustering of Applications with Noise)聚类算法是一个被较常使用的机器学习算法,已被广泛的应用到异常值检测、模式识别等领域 [3] [4] [5]。
由于滑坡影响因素之间复杂且关系耦合,建立数学模型存在对复杂的问题解释不足 [6]。考虑到滑坡的众多影响因素对滑坡综合影响下,最终都是通过滑坡的累积位移变化体现出来。因此本文采用数据挖掘领域 [4] 的DBSCAN聚类算法对滑坡累积位移序列数据作滑坡阶段划分研究。
2. 算法介绍
2.1. DBSCAN算法的基本原理
DBSCAN算法是一种基于密度聚类的算法 [3],一般假设样本的类别能通过样本的分布情况即紧密程度来确定。同属于一个类别的样本,样本之间是紧密相连的,也就是说,在某类别的任一样本局部一定有相同类别的样本存在,得到一个聚类类别,就是将密度相连的样本归为一个类别。通过将所有各组密度相连的样本划为各个不同的类别,最后就得到所有聚类的类别结果。
DBSCAN描述样本集的紧密程度是基于一组领域,参数(p, N)用来描述领域的样本分布的紧密程度。其中,p是样本的领域距离,N是样本的p领域中样本个数的阈值,(p, N)是算法初始设定的固定值,对于样本集 ,DBSCAN算法的具体密度描述定义如下:
1) p领域:对于 ,其p领域包含样本集D与 的距离不大于p的子样本集,即 ,样本 的密度记为 。
2) 核心对象:对于任一样本 ,如果其p领域对应的密度 至少包含N个样本,即 ,则 是核心对象。
3) 非核心对象:对于任一样本 ,如果其p领域对应的密度 包含少于N个样本,即 ,则 是非核心对象。
4) 密度直达:如果样本 在样本 的p领域中,且 是核心对象,则称 由 密度直达。
5) 密度可达:对于 和 ,如果存在样本序列 ,有 ,,且 由 密度直达,则称 由 密度可达。即,密度可达具有传递性。此时序列中的传递样本全部为核心对象。
6) 密度相连:对于 和 ,如果存在核心对象样本 ,使 和 均由 密度可达,则称 和 密度相连。
2.2. DBCSCAN算法与统计量M
DBSCAN聚类算法的特点在于对聚类簇的个数未知,有可能大于我们需要划分的三个阶段,若聚类簇的个数k大于3,则需要考虑合并聚类簇,使得滑坡累积位移数据聚类为3个聚类簇。由于本文实际上为应用DBSCAN算法对滑坡的累积位移序列作阶段划分,可理解为分割问题。在累积位移序列中,聚类簇的分界点可以考虑只存在于非核心对象中,问题转化为在k-1个聚类分界点中选择出最合适的两个分界点作为滑坡的阶段划分的分割点。
因此,考虑选取一个合适的统计量M,利用启发式的分割算法,选择最小的两个统计值m,将滑坡划分为三个阶段。选取的两个最优阶段划分时刻点同时也要保持使得分割成的子序列大于20。统计值m的确定用分段函数 的函数值表示
(1)
其中, 为距离 最近的两个核心对象。 为距离 最近的两个核心对象的密度值。
选用分段函数 的函数值作为样本 对应的统计值m,若样本点 为非核心对象时,以样本点 的密度值与距离样本点 最临近的两个核心对象的密度的比值之和作为其对应的统计值m。若样本点为核心对象时,以样本点 的对数密度值为其对应的统计值m,显然核心对象的统计值m是大于非核心对象的统计值m的。统计值m越小,表示核心对象与非核心对象之间的差异越大。核心对象的密度值越大,可以表示滑坡处于一个稳定发育的状态,非核心对象的密度值越小,可以表示滑坡对于前一段时间的状态发生偏离,处于一个不稳定的快速变形发育状态。因此用统计量M表示滑坡在时刻i的密度阈值小于N时,从稳定发育状态转变为快速变形发育状态的突变程度。
2.3. DBSCAN算法的参数确定
2.3.1. p领域的半径确定
由于选用的滑坡累积位移序列,对于不同的滑坡阶段,滑坡的位移差显然是不同的,如果选择确定数值的半径p,对于滑坡的前期阶段由于位移差较小,导致前期样本的密度较大,在滑坡后期阶段的位移差较大,导致后期样本的密度又较小。因此,选择样本 的比例为半径,即
(2)
参数 的确定:对于每个样本点 计算一个 :
(3)
取全部样本点的平均值为 :
(4)
2.3.2. 密度阈值N的确定
由于在p领域中样本点的密度计算时,包含样本点本身。选取全部样本点的平均值为参数p时,相应地,密度阈值N设定应该保持样本点包含最邻近的两个样本点在其p领域中,即密度阈值N应该设定为3。
3. 滑坡实例分析
新滩滑坡位于三峡西陵峡中的新滩镇,本文取1978年1月到1985年6月共90个月的累计位移监测数据 [2]。从图1新滩滑坡的累积位移图中可以看出在滑坡的稳定发育状态下,新滩滑坡的位移差较小;在滑坡的不稳定发育状态下,滑坡的位移差较大。新滩滑坡呈现出较明显的阶段发育特性。在稳定发育状态下的新滩滑坡数据呈现密度较为集中,相应地,此时刻的滑坡数据具有较大的密度值;在不稳定发育状态下的新滩滑坡数据较为分散,此时刻的滑坡数据具有较小的密度值。滑坡从稳定发育状态下的高密度值下降到不稳定发育状态下的低密度值,可以表征滑坡的变形发育的剧烈程度。
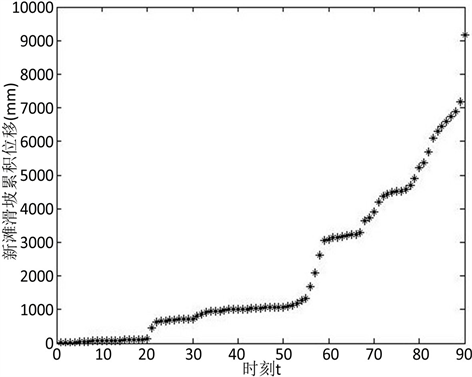
Figure 1. Cumulative displacement of Xintan landslide
图1. 新滩滑坡累积位移
本文中,以全部相邻时刻间的位移变化量的平均值作为参数 ,。密度阈值为3,实验结果表明当半径参数p选取的较小时,DBSCAN算法将滑坡累积位移序列聚类的簇是远远大于三个阶段的。此时,时刻12~13、17~22、31~32、55~58、70、79组成了滑坡的非核心对象,因此DBSCAN算法对新滩滑坡的序列数据聚类成了7个聚类簇。
由图2的新滩滑坡密度图的结果我们知道,算法将新滩滑坡的累积位移序列数据聚类成7个聚类簇,此时需要将7个聚类簇进一步合并成3个聚类簇。本文将从6个聚类簇的分界点中选择出最好的两个分界点作为滑坡的聚类簇的个数缩小后的最优分界点。由图3新滩滑坡密度统计值可以看出在时刻20~21的时候,滑坡得到最小的密度统计值。表明在这一时刻,滑坡从稳定的状态变化到不稳定的状态的程度最剧烈,选取时刻20~21为滑坡的阶段划分点。在时刻56~58的时候,滑坡得到第二小的密度统计值,而且与时刻20之间构成的子序列长度是大于20的,因此中间时刻57为滑坡的阶段划分点。时刻0~20为新滩滑坡发育变形的第一阶段,时刻21~57为发育变形的第二阶段,时刻58~90为发育变形的第三阶段。
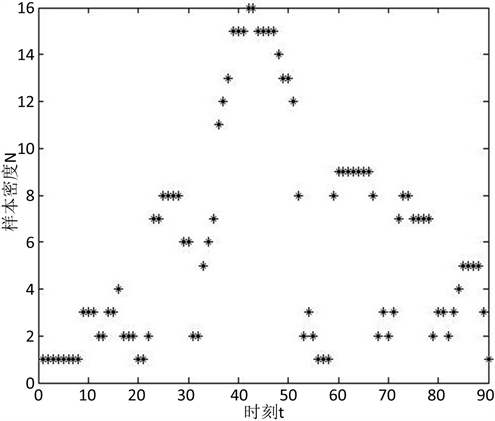
Figure 2. Sample density of Xintan landslide
图2. 新滩滑坡的样本密度
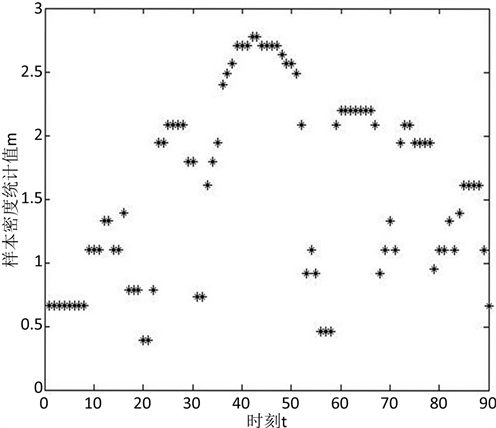
Figure 3. Sample density statistics m of Xintan landslide
图3. 新滩滑坡的样本密度统计值m
4. 结论
本文利用滑坡累积位移序列,采用DBSCAN算法对滑坡进行阶段划分,并进一步对聚类簇合并成3个聚类簇,本文设计的密度统计值M能有效地筛选出滑坡累积位移序列中最合适的序列分割点,作为滑坡阶段的划分点。实验结果与实际检测结果吻合,证明算法能有效地运用于滑坡的阶段划分。
基金项目
中国地质大学长江流域地质过程及资源环境研究计划(编号:CUGCJ1802)。
文章引用
卢静云,罗文强,李 燕. 基于DBSCAN算法的滑坡阶段划分
Division of Landslide Stages Based on DBSCANAlgorithm[J]. 应用数学进展, 2020, 09(02): 166-171. https://doi.org/10.12677/AAM.2020.92019
参考文献
- 1. 罗文强, 李飞翱, 刘小珊, 黄丽. 多元时间序列分析的滑坡演化阶段划分[J]. 地球科学, 2016, 41(4): 711-717.
- 2. 黄丽, 樊孝菊, 罗文强. 基于有序样品聚类最优二分割算法的滑坡演化阶段划分[J]. 湖北文理学院学报, 2015, 36(2): 13-16.
- 3. 韩梅. 基于改进DBSCAN的复杂工业过程建模数据异常点检测研究[D]: [硕士学位论文]. 天津: 天津工业大学, 2016.
- 4. 黄雯. 数据挖掘算法及其应用研究[D]: [硕士学位论文]. 南京: 南京邮电大学, 2013.
- 5. 秦佳睿. DBSCAN聚类算法的改进及在数据分析系统中的应用[D]: [硕士学位论文]. 长沙: 长沙理工大学, 2017.
- 6. 韩舸. 基于外因响应的分阶段滑坡位移预测模型研究[D]: [硕士学位论文]. 武汉: 中国地质大学, 2012.