Advances in Applied Mathematics
Vol.
09
No.
07
(
2020
), Article ID:
36491
,
10
pages
10.12677/AAM.2020.97120
Plastic Simulation of Elliptical Orifice with Double Cracks in One-Dimensional Hexagonal Quasi-Crystals
Jinyan Liang, Wu Li
School of Mathematics, Taiyuan University of Technology, Jinzhong Shanxi

Received: Jun. 26th, 2020; accepted: Jul. 7th, 2020; published: Jul. 14th, 2020

ABSTRACT
In this paper, the problem of elliptical hole with double cracks in one-dimensional hexagonal quasi-crystals is simulated. By using conformal mapping method, the physical plane problem that is difficult to deal with in quasi-crystals is transformed into a familiar and regular mathematical plane problem. Based on the existing theory, the size of the cohesive force area at the tip of the double cracks in the elliptical hole is obtained. In the case of limit, it is the same as the existing result.
Keywords:One-Dimensional Hexagonal Quasi-Crystal, Elliptical Orifice with Double Cracks, Complex Function

一维六方准晶中带双裂纹的椭圆孔口问题的塑性模拟
梁晋燕,李梧
太原理工大学数学学院,山西 晋中

收稿日期:2020年6月26日;录用日期:2020年7月7日;发布日期:2020年7月14日

摘 要
本文主要对一维六方准晶中带双裂纹椭圆孔口问题进行了裂纹尖端的塑性模拟,利用保角映射法,将准晶中难处理的物理平面问题转变为我们所熟悉的、有规则的数学平面问题,基于已有的理论,最后得到椭圆孔所带双裂纹的尖端内聚力区域的尺寸大小,并且在极限的情况下与已有结果相同。
关键词 :一维六方准晶,带双裂纹的椭圆孔口,复变函数

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
数学和力学界对于固体中带有裂纹的孔口类问题一直以来都非常关注,而准晶作为一种新的固体结构材料 [1] 必会引起广大学者的重视。经研究发现,要想深入探究准晶的弹性问题,就不仅仅需要探究其内的声子场,还需去探究与声子场相耦合的相位子场。准晶自被发现以来,对带裂纹的准晶进行塑性模拟的研究就变得极其活跃,建立物理模型的方法则成为了大部分学者的选择 [2]。很多学者灵活地运用复变函数中的保角映射法、复势法以及傅里叶变换等方法,同时结合物理模型,对各类带裂纹的准晶孔口问题都做了很有意义的探究 [3] [4] [5] [6],并逐渐在该知识领域里形成了系统的知识网络。本文基于Barenblatt和Dugdale的理论观点 [7],讨论了一维六方准晶中带双裂纹椭圆孔口的问题,并对其裂纹尖端进行了塑性模拟。
2. 一维六方准晶中带双裂纹椭圆孔口问题的塑性模拟
2.1. 一维六方准晶中的基本公式
一维六方准晶中的广义Hooke定律为 [8]
(1)
其中,
是声子场和相位子场的应变分量,
是这两个场的应力分量,
是耦合的弹性常数,
、
是声子场、相位子场的独立弹性常数,且有
。几何方程为
(2)
其中
,这里
是指声子场的各位移分量,v指相位子场的位移。
其平衡方程为(不计体力)
(3)
上述的就是广义胡克定律、几何方程以及平衡方程构成了弹性理论中一维六方准晶的基本方程。
在这里,我们以图1模型中的坐标轴
为准晶的准周期方向,由于准晶的几何对称性,所以裂纹穿过
轴时,即横穿一维六方准晶中的准周期方向时,变形就不再随着
的变化而变化,故有
(4)
把式(4)代入式(1)~(3),上述问题就能被简化为两个问题来求解,其中一个问题可以依据文献 [9] 中介绍的经典弹性理论求解 [10],接下来我们主要讨论第二个问题,即
(5)
(6)
(7)
(8)
将上文的(8)式代入到(5)、(6)后,得到的结果再代入(7),得到
,,其中,
。
在
时,有
(9)
显然,该问题最后可以化为方程组(9)去求解。显然地,我们可以用两个解析函数的实部来表示
和v [11],即
(10)
其中Re代表复变函数的实部,
。
2.2. 一维六方准晶中带双裂纹椭圆孔口问题的塑性模拟
如图1模型所示,其中a为椭圆孔口的长半轴,b为椭圆孔口的短半轴,孔口每边的裂纹长为
,如2.1中所述,
轴为准周期方向,裂纹穿透该方向。方程(9)为该二维弹性问题的控制方程 [12],这种情形下,平衡方程为
(11)
根据Dugdale的观点,在裂纹的尖端附近存在“内聚力区域”,假设屈服应力是
,其裂纹尖端附近的塑性区域长为R (如图1),则边界条件为:
(12)
这个边值问题可以归结为以下两个子问题的叠加:
(13a)
与
(13b)

Figure 1. Plastic simulation of elliptical orifice with double cracks in one-dimensional hexagonal quasi-crystals
图1. 一维六方准晶中带双裂纹椭圆孔口问题的塑性模拟
对于问题(13a),若准晶只在椭圆孔口以及双裂纹的表面受到了
的作用,而在无穷远处没有受到任何外应力的作用,那么,除去一个常数项外,这两个问题的解是等价的。现在,我们考虑只在椭圆孔口、所带双裂纹的表面受到
作用的问题,该问题的边界条件为
(14)
这里裂纹面的相位子场应力
只是从物理角度的一个假设,其具体的测量值到目前还没有相关的报道,也可以简单假设为
。下面求解边值问题(9)与(14)。
令
,若
为解析函数,则有
(15)
若
(16)
则依Cauchy-Riemann关系,有
(17)
结合(5)、(6)、(8)、(10)、(15),有
(18)
利用式(17),上式可写为
(19)
其中
,。由(19)可知,
,,任一个函数
,都满足
,从而有
(20)
若L是带有双裂纹的椭圆孔口,则式(14)就变为
(21)
作保角映射
(22)
其中
(23)
单位圆周
被映射为带双裂纹的椭圆孔L,
平面上的单位圆也被保角映射到z平面上带有双裂纹椭圆孔的外部,且有
,,,。
令
,则有
(24)
把该结果代入(21)中,再把单位圆上的点
代入后,得
给上述两式的等号两端各乘以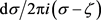 ,再沿着单位圆周
进行积分,得
,再沿着单位圆周
进行积分,得
(25)
(26)
因为在单位圆
内,
和
是解析函数,那么根据Cauchy积分定理,有
(27)
由式(22),得
(28)
由式(28),以及
,有
。
、
可以展成下面的Taylor级数,因为它们都是
内的解析函数,
而
与
可看作
, 在单位圆周
上的边值,所以(25)与(26)中的
与
是
内的函数
、
的边值。利用文献 [7] 中所提到的无穷远处的Cauchy积分公式,即,
,有
(29)
把式(29)和式(28)代入式(25)以及(26),可得
(30)
由式(28)知,
在单位圆外
是解析的,在
上是连续的,利用无穷远处的Cauchy积分公式,并令其结果为
(31)
将式(31)代入式(30)得
(32)
由上式可得
(33)
利用式(24),有
(34)
将上式代入式(19),得
(35)
对于问题(13b),边界条件(13b)可以写为
(36)
做相同的保角变换(22),并把式(24)代入式(36),整理后得:
同上一个问题类似,得:
由Cauchy积分定理有:
结合式(28),(29),(31)得到:
求解上式,可得:
(37)
利用式(24),有
(38)
将上式代入式(19),得
上式说明材料常数和应力的分布是不相关的,这个结论和经典弹性理论是吻合的。解上述方程组以及(35),可得到应力
、
、
、
。
3. 应力强度因子的计算
材料会发生塑性变形是因为在裂纹尖端有高度的应力集中,那么应力的最大值就超过了原材料的塑性极限,同时会在裂纹尖端产生所谓的塑性区 [13]。而裂纹顶端附近的应力与位移均由应力强度因子所控制 [14],因此去求解材料的应力强度因子无论在断裂力学还是弹性力学中都显得极其重要。
(39)
该公式用来计算
平面上的应力强度因子,其中
为与裂纹的顶端相对应的点。
对于问题(13a)而言,由式(28)可知
(40)
又由式(31)有
(41)
从而有
(42)
结合(39),可得在
处,有
(43)
这是裂纹尖端附近的声子场应力强度因子与、相位子场应力强度因子,同样的方法可计算得问题(13b)的应力强度因子为
(44)
4. 裂纹尖端塑性区尺寸的计算
根据Dugdale的观点,在虚拟的裂纹尖端总应力强度因子应该等于零,即
,那么一维六方准晶中,在裂纹尖端均需要满足这个等式,利用上文中求得的应力强度因子,代入该等式,便可以得到这两个问题中塑型区域的尺寸大小,因此我们有:
对于一维六方准晶中带双裂纹的椭圆孔口问题,根据上文分析以及文献 [8],我们可知问题中的塑性区域R的尺寸大小均由下式确定
当在这个问题中,我们令
,那么就有
计算过程如下:
当
时,
,则
,且有
,则对于式
, 式中有
,经过化解,得
,再令
,有
。
因此解得
。此时问题转化为了中心裂纹问题,裂纹长为
,而式
与式
是近似相等的,其中a由c代替,而这个结果与文献 [8] 中的结果是相吻合的。
5. 结语
本文基于Dugdale的观点,对一维六方准晶中带双裂纹椭圆孔口的反平面剪切问题进行了裂纹尖端的塑性模拟,并获得了一维六方准晶带双裂纹椭圆孔口问题中裂纹尖端发生塑性变形时内聚力区域的尺寸,这对于弹性体塑性变形的研究以及断裂力学都是有一定意义的,同时也为之后这方面的研究提供了一个理论参数。
文章引用
梁晋燕,李 梧. 一维六方准晶中带双裂纹的椭圆孔口问题的塑性模拟
Plastic Simulation of Elliptical Orifice with Double Cracks in One-Dimensional Hexagonal Quasi-Crystals[J]. 应用数学进展, 2020, 09(07): 1006-1015. https://doi.org/10.12677/AAM.2020.97120
参考文献
- 1. 董闯. 准晶材料[M]. 北京: 国防工业出版社, 1998: 58-175.
- 2. 王仁卉, 胡承正, 桂嘉年. 准晶物理学[M]. 北京: 科学出版社, 2004.
- 3. Fan, T.Y., Li, X.F. and Sun, Y.F. (1999) A Moving Screw Dislocation in a One-Dimensional Hexagonal Quasicrystals. Acta Physica Sinica (Overseas Edition), 8, 288-295. https://doi.org/10.1088/1004-423X/8/4/007
- 4. 皮建东, 刘官厅, 郭怀民. 一维六方准晶狭长体中共线裂纹问题的精确解[J]. 内蒙古师范大学学报(自然科学汉文版), 2006, 35(4): 391-396.
- 5. Li, X.F. and Fan, T.Y. (1999) A Straight Dislocation in One Dimensional Hexagonal Quasicrystals. Physica Status Solidi (B), 212, 19-26. https://doi.org/10.1002/(SICI)1521-3951(199903)212:1<19::AID-PSSB19>3.0.CO;2-O
- 6. Liu, G.T., Guo, R.P. and Fan, T.Y. (2003) On the Interaction between Dislocations and Cracks in One-Dimensional Hexagonal Quasicrystals. Chinese Physics, 2, 1149-1155. https://doi.org/10.1088/1009-1963/12/10/317
- 7. 范天佑. 断裂理论基础[M]. 北京: 科学出版社, 2003.
- 8. 范天佑. 准晶数学弹性理论及应用[M]. 北京: 北京理工大学出版社, 1999.
- 9. 徐芝纶. 弹性力学: 上册[M]. 第3版. 北京: 高等教育出版社, 1990.
- 10. Ding, D.H., Yang, W.G., Hu, C.Z., et al. (1993) Generalized Elasticity Theory of Quasicrystals. Physical Review B, 48, 7003-7010. https://doi.org/10.1103/PhysRevB.48.7003
- 11. 刘官厅. 准晶弹性的复变方法与非线性发展方程的显示解[M]. 呼和浩特: 内蒙古人民出版社, 2005.
- 12. Liu, G.T., Fan, T.Y. and Guo, R.P. (2004) Governing Equations and General Solutions of Plane Elasticity of One-Dimensional Quasicrystals. International Journal of Solids and Structures, 41, 3949-3959.
https://doi.org/10.1016/j.ijsolstr.2004.02.028
- 13. 丁棣华, 王仁卉, 杨文革, 等. 准晶的弹性、塑性与位错[J]. 物理学进展, 1998, 18(3): 223-260.
- 14. Ding, D.H., Yang, W.G., Hu, C.Z., et al. (1994) Linear Elasticity Theory of Quasicrystals and Defects in Quasicrystals. Materials Science Forum, 150-151, 345-354. https://doi.org/10.4028/www.scientific.net/MSF.150-151.345









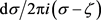 ,再沿着单位圆周
进行积分,得
,再沿着单位圆周
进行积分,得