Advances in Applied Mathematics
Vol.
12
No.
05
(
2023
), Article ID:
65102
,
8
pages
10.12677/AAM.2023.125212
基于优化Tikhonov最小二乘模型的曲面重建
付飞凡,杨奋林*,刘广英
吉首大学数学与统计学院,湖南 吉首
收稿日期:2023年4月7日;录用日期:2023年4月29日;发布日期:2023年5月10日

摘要
曲面3D重建是通过SfS系列方法从灰度图像中获取梯度场后,采用L2范数建立深度函数的能量泛函进行重建,这是一个不适定问题。本研究一方面通过将三角测量获取的粗糙深度图Z0与深度函数进行拟合作为Tikhonov正则项,将其转化为适定问题,并用L曲线选取合适的正则化参数;另一方面,利用先离散再优化的方法将上述问题表示为Sylvester矩阵方程,使用Hessenberg-Schur方法求解得到待重建曲面。数值实验表明,优化后的模型抑制噪声和偏差的效果更优,重建精度更高。
关键词
曲面重建,最小二乘技术,Tikhonov正则项,L曲线,Sylvester方程

Surface Reconstruction Based on Optimized Tikhonov Least Squares Model
Feifan Fu, Fenlin Yang*, Guangying Liu
College of Mathematics and Statistics, Jishou University, Jishou Hunan
Received: Apr. 7th, 2023; accepted: Apr. 29th, 2023; published: May 10th, 2023

ABSTRACT
Surface 3D reconstruction is to obtain gradient field from gray image by SfS series method, and then reconstruct it by using L2 norm to establish the energy functional of depth function, which is an ill-posed problem. In this study, on the one hand, the rough depth map Z0 obtained by triangulation is fitted with the depth function as Tikhonov regular term, which is transformed into an adaptive problem, and the appropriate regularization parameters are selected with L curve. On the other hand, the above problems are expressed as Sylvester matrix equations by the first discretization and then optimization method, and the reconstructed surfaces are obtained by Hessenberg-Schur method. Numerical experiments show that the optimized model can suppress the noise and deviation better, and the reconstruction accuracy is higher.
Keywords:Surface Reconstruction, Global Least Squares Technique, Tikhonov Regular Term, L Curve, Sylvester Equation

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
三维重建是利用测得曲面的二维梯度场或表面法向的矢量数据来恢复物体三维信息的过程,它对许多应用都是必不可少的,如地震成像 [1] 、Hartmann波前检测 [2] 、光栅投影 [3] 和三维精密测量 [4] 等。假
设图像通过正交投影获得,其3D表面为 ,它的梯度场可以表示为 。最
基本的曲面重建方法是基于线积分,并优化局部代价函数,但是它不能添加任何形式的正则项。Frankot和Chellappa [5] 以及Kovesi [6] 他们分别使用复杂的傅里叶变换和Shapelets,这两种方法都是周期性的,并不现实。Horn和Brooks [7] 提出了变分法,此方法目的在于根据重建曲面上的边界条件最小化最小二乘泛函,后来有很多学者也遵循这一思路。Harker [8] 等人将最小化泛函问题表达为一个半正定的Sylvester方程,提高了求解速度。
笔者借鉴Horn和Harker等人的思想,在最小二乘积分重建技术的基础上引入深度图与深度函数拟合后的Tikhonov正则项,利用L曲线选取最佳参数从而优化了Tikhonov最小二乘模型,提高重建精度。在Sylvester方程下使用Hessenberg-Schur (HS)算法进行求解。最后通过数值实验与现有的算法进行对比。
2. 最小二乘泛函曲面重建
2.1. 最小二乘模型
假设图像是通过正交投影获得的,并且表面具有明确的形式 ,将梯度空间参数细化为
, 。获取高度z即解的前提是有一个被噪声破坏的梯度场。假设噪
声是高斯噪声,最小二乘成本函数的连续形式为 [8] :
(1)
式中 和 分别代表测量梯度,这个成本函数是函数差的平方项的体积。利用有限差分的思想,此成本函数在矩形网格上等价的离散形式为:
(2)
式中 和 表示测量得到的梯度矩阵; 表示F范数。由于微分是一个线性算子,导数可以写成一个简单的矩阵乘法,即线性变换:
(3)
这里“≈”表示最小平方意义上的相等。 和 分别是x和y方向的有限差分矩阵。 会对x方向的微分产生影响。因此,在测量的梯度场 和 中,最小二乘意义上最接近的曲面是以下成本函数的最小值:
(4)
2.2. 带有Tikhonov正则项的最小二乘模型
最常见的正则化项是解的范数的一个界限 [9] 。在离散意义上,解的F范数为:
(5)
它是一个有效的0阶正则化项。用最右端的形式书写,方程(5)就满足Sylvester方程的框架。其中 和 是单位矩阵。对于1阶正则化项而言,它可以利用函数沿单位向量 的方向导数推导出曲面上某一点的最大方向导数,进而得到一个限定曲面陡度的正则化项,其离散化为:
(6)
类似的可以导出一个二阶正则化项,它是曲面平均曲率的边界:
(7)
对于从梯度重建曲面的问题而言,要最小化的函数取决于2D曲面而不是向量。所以Tikhonov正则化的常用方法不直接适用。为了推导出2D域的适当函数,从方程(4)开始,通过比较方程(5)~(7),将矩阵 和 分别定义为x和y方向上的一般“平滑”算子。因此,Tikhonov最小二乘泛函的一般形式如下:
(8)
这里 是由三角测量得到的粗糙深度图,将其作为表面的先验估计。然而将先验估计值纳入算法中的事实可能会对光度立体技术在应用过程中产生巨大的影响。下一节将在L曲线框架中考虑正则化参数的选择,以此来优化Tikhonov最小二乘模型。
3. 模型优化与求解
3.1. 正则化参数的选择
L曲线 [10] 是在未知其他噪声特性的情况下选择正则化参数的最简单方法之一。L曲线是 的曲线,其中 是最小平方成本函数:
(9)
是标准形式的正则化项:
(10)
因此,L曲线是最小二乘残差和正则化项大小相互作用的可视化结果。将x方向和y方向导数算子的奇异值分解(SVD)表示为
(11)
(12)
一旦计算了导数矩阵的SVD,L曲线上的点可以计算为:
(13)
以及
(14)
上述式子中 , , 。根据F范数在正交变换下的不变性,由于 和 是对角矩阵,这些计算成本比SVD的计算成本更小,因此可以通过计算L曲线上的几个点来确定适当的正则化参数,将最佳参数值带入方程(8)中,从而达到优化模型的目的。
3.2. 建立Sylvester方程求解成本函数
若待重建图像有 个采样点,则方程(8)中系数矩阵 和 的大小为 。虽然 和 是稀疏矩阵,空间复杂度较高,但Harker使用Sylvesyer方程将系数矩阵大小降低为 。从而本研究将成本函数公式(8)中的参数利用L曲线优化后对 进行微分并使得它的值为0,得到该函数相应的正规方程:
(15)
此方程是未知曲面 中的Sylvester方程。对于曲面重建问题,本研究考虑“平滑”算子 , 在这种情方程(15)可以改写为:
(16)
方程(16)也是一个Sylvester方程,但由于 和 有相同的特征值,所以此方程没有唯一解。要想求得唯一解,可以采取HS算法 [8] 求解。首先使用Householder变换将矩阵 和 分解为上三角形式的矩阵(11)和(12),Householder矩阵 和 是正交的,不会影响解的数值精度,显然有 , 。方程(16)可以化简为:
(17)
此方程左乘 右乘 可得:
(18)
其中 。
令 , , , ,方程(18)可以写为:
(19)
此方程可以写为以下形式:
(20)
它等价于下面方程组:
(21)
以 中元素为未知量进行方程组(21)的求解,将矩阵重新组合,得到待重构的曲面 为:
(22)
4. 实验结果与分析
为了将更新参数后的结果与现有的方法进行对比,本研究进行了以下实验:
1) 用理想数据合成一个待重建的地形图。利用蒙特卡洛测试,比较成本函数的误差,并将本研究中的重建结果图与现有方法结果图进行对比,分析方法的鲁棒性;
2) 采用蒙特卡洛测试,就不同尺寸图像的计算时间而言,将现有方法的结果与本研究中的结果进行对比。
本研究选取了尺寸大小为 的合成地形图,其类似于MATLAB中的“峰值”检测,测试曲面及其梯度场如图1所示。
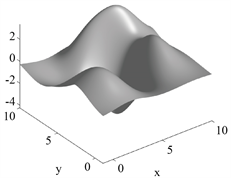 (a) 测试曲面Z
(a) 测试曲面Z
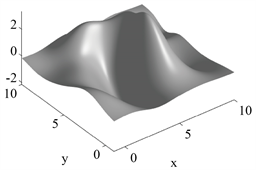 (b) 梯度场Zx
(b) 梯度场Zx
 (c) 梯度场Zy
(c) 梯度场Zy
Figure 1. Topographic map and its gradient field to be reconstructed
图1. 待重建的地形图及其梯度场
将全局最小二乘(Global Least Squares, GLS)以及Dirichlet边界结果与本研究得到的结果进行比较。选择GLS的原因在于,一方面它和本研究一样,都是在Sylvester方程框架下进行求解,另一方面,当梯度场被高斯噪声破坏后,GLS是一个标准的解决方案;选择Dirichlet边界的原因在于,确定曲面的边界可以减少自由度的数量,从而减少未知数的数量,在这种情况下,Dirichlet问题的解是唯一的,同样可以利用Sylvester方程求解,并且对异常值具有极强的鲁棒性。
根据现有文献的方法,将 的高斯噪声添加到梯度场中,当受高斯噪声影响时,解析梯度不再是可积的。图2展示了图1中测试曲面Z被高斯噪声破坏时的梯度。
为了使得从被噪声破坏的梯度场中重建曲面的效果更好,本研究利用L曲线算法,选取100个要计算的L曲线上的点数,从中选取正则化参数 的最佳值。 的选择结果如图3中(a)所示。从图中可以看出,当 时为最佳值,优化模型后重建的曲面如图3中(b)所示。图3中的(c)和(d)分别为GLS以及Dirichlet边界重建曲面的效果图,可以看出利用L曲线以及Dirichlet边界重建的曲面抑制噪声以及偏差的效果更好,但是本研究的方法在边界上要比Dirichlet边界更稳定更平滑;GLS以及本研究方法整体效果更优,虽然本研究方法在左侧和右侧边缘处高度值恢复有误差,边缘处有少量锯齿状的不稳定值存在,但是比GLS重建表面更光滑。
 (a) 被噪声破坏后的梯度场Zx
(a) 被噪声破坏后的梯度场Zx
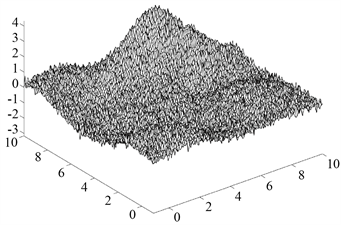 (b) 被噪声破坏后的梯度场Zy
(b) 被噪声破坏后的梯度场Zy
Figure 2. Gradient of test surface Z damaged by Gaussian noise
图2. 测试曲面Z被高斯噪声破坏时的梯度
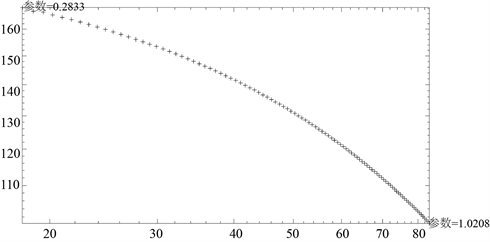 (a) L曲线
(a) L曲线
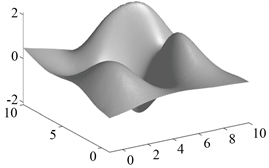 (b) Tikhonov (L曲线)
(b) Tikhonov (L曲线)
 (c) GLS
(c) GLS
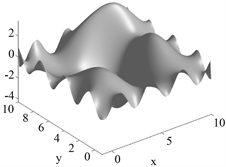 (d) Dirichlet边界
(d) Dirichlet边界
Figure 3. L curve and the reconstructed surface renderings under the three methods
图3. L曲线以及三种方法下的重建曲面效果图
为了更进一步分析三种方法的鲁棒性,采用均方误差(MSE)以及相对均方误差(RMSE)来衡量。
, (23)
其中, 表示图像像素点 处测得的高度, 表示真实高度。所得MSE和RMSE如表1所示,分别展示了三种方法下的重建误差。
Table 1. Reconstruction error of each algorithm under noise σ = 0.05 and surface size of 128 × 128
表1. 在噪声 下表面尺寸为128 × 128下各算法的重建误差
从表1可以看出,本研究所采用方法比另外两种方法下的误差显著降低,其主要原因在于本研究中的方法通过惩罚曲面的平均曲率来对成本函数起作用,因此是一个低通型滤波器,可以达到消除噪声的目的,鲁棒性增强;GLS受异常值扰动的影响较大,因此鲁棒性弱于本研究中的方法;Dirichlet边界在图像边缘处鲁棒性较弱。
不同尺寸图像的计算时间比较的结果将在表2中展示。
Table 2. The computation time of the algorithm
表2. 算法的计算时间
表2结果显示,通过L曲线优化后的模型在小尺寸图像的重建上有着较强的优势,比另外两种方法快了将近0.1 s;在中等尺寸和大尺寸图像的重建中弱于GLS;虽然大尺寸图像上Dirichlet边界优势显著,但本研究仍具有较好的应用价值。
5. 结语
笔者通过引入L曲线来选取参数 的最优值,从而优化了Tikhonov最小二乘模型。利用有限差分思想将模型进行离散,使得离散后的解满足Sylvester方程。利用HS算法求解降低计算时间。仿真实验表明,在理想情况下,优化模型后的方法能够有效抑制噪声和偏差,在小尺寸图像上比五点差分格式的GLS耗时更短,误差更小;优化模型后重建出的三维图精度更高,更接近原始曲面,整体效果更优。未来考虑具有边界条件的Tikhonov正则化,设计出更快速有效的数值方法,进一步缩短重建时间,提高重建精度和质量。
基金项目
2022年湖南省教育厅科学研究项目(22A0368);吉首大学校级科研项目(Jdy22012)。
文章引用
付飞凡,杨奋林,刘广英. 基于优化Tikhonov最小二乘模型的曲面重建
Surface Reconstruction Based on Optimized Tikhonov Least Squares Model[J]. 应用数学进展, 2023, 12(05): 2086-2093. https://doi.org/10.12677/AAM.2023.125212
参考文献
- 1. Feng, F., Li, C.W. and Zhang, S.J. (2018) Wavefront Reconstruction by a Defocused Shack-Hartmann Sensor Based on Moment of Spot. Acta Optica Sinica, 38, Article ID: 0628001. https://doi.org/10.3788/AOS201838.0628001
- 2. Fu, C.H., He, Y.G., Liu, W.J., et al. (2015) Hartmann-Shack Sensor with Dual-Wedge Micro-Scanning in Wavefront Detection Technology. Journal for Light and Electronoptic, 44, 2813-2818.
- 3. 何煦, 袁理. 基于子孔径斜率离散采样的波前重构[J]. 光学精密工程, 2016, 24(1): 20-29.
- 4. Nie, E., Hu, X.Q., Dong, B., et al. (2018) Study of Phase Retrieval Algorithm Based on Hybrid Unwrap-ping under Mosaic Pupil of Regular Hexagons. Optical Technique, 44, 519-524.
- 5. Frankot, R. and Chellappa, R. (1988) A Method for Enforcing Integrability in Shape from Shading Algorithms. IEEE PAMI, 10, 439-451. https://doi.org/10.1109/34.3909
- 6. Kovesi, P. (2005) Shapelets Correlated with Surface Normals Produce Sur-faces. Tenth IEEE International Conference on Computer Vision (ICCV’05), 2, 994-1001. https://doi.org/10.1109/ICCV.2005.224
- 7. Horn, B. and Brooks, M.J. (1985) The Variational Approach to Shape from Shading. Computer Vision Graphics & Image Processing, 33, 174-208. https://doi.org/10.1016/0734-189X(86)90114-3
- 8. Harker, M. and O’Leary, P. (2008) Least Squares Surface Reconstruction from Measured Gradient Fields. IEEE Conference on Computer Vision & Pattern Recognition, 1-7. https://doi.org/10.1109/CVPR.2008.4587414
- 9. Harker, M. and O’Leary, P. (2015) Regularized Reconstruction of a Surface from Its Measured Gradient Field Algorithms for Spectral, Tikhonov, Constrained, and Weighted Regulari-zation. Journal of Mathematical Imaging and Vision, 51, 46-70. https://doi.org/10.1007/s10851-014-0505-4
- 10. Hansen, P.C. and O’Leary, D.P. (1993) The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems. SIAM Journal on Scientific Computing, 14, 1487-1503. https://doi.org/10.1137/0914086
NOTES
*通讯作者。
