Advances in Applied Mathematics
Vol.
12
No.
10
(
2023
), Article ID:
73483
,
13
pages
10.12677/AAM.2023.12100407
一类特殊链环的Kauffman多项式
徐芷微
辽宁师范大学数学学院,辽宁 大连
收稿日期:2023年9月6日;录用日期:2023年10月1日;发布日期:2023年10月10日

摘要
Kauffman多项式在纽结理论中占据一定地位,是纽结和链环中最有用的双变量Laurent多项式不变量之一,其已经成为量子拓扑的基本构建块。本文主要研究一类特殊不定向链环——复叠链环,研究了这类链环的Kauffman多项式以及Kauffman多项式对应的生成函数。借助直线型链环的Kauffman多项式对复叠链环的Kauffman多项式进行计算,这为研究定向复叠链环的Kauffman多项式以及BLM/Ho多项式奠定基础。
关键词
Kauffman多项式,递归关系式,生成函数

The Kauffman Polynomials of a Special Class of Links
Zhiwei Xu
School of Mathematics, Liaoning Normal University, Dalian Liaoning
Received: Sep. 6th, 2023; accepted: Oct. 1st, 2023; published: Oct. 10th, 2023

ABSTRACT
The Kauffman polynomial is probably the most useful two-variable polynomial invariants of knots and links. It generalizes the Jones polynomial, and it has become basic building blocks of quantum topology. In this paper, we mainly study a special type of links—the covering links, and we study the Kauffman polynomials of the link and the corresponding generating functions. The Kauffman polynomials of the covering links is calculated by using the Kauffman polynomials of linear links, which lays a foundation for the study of Kauffman polynomials and BLM/Ho polynomials of the oriented covering links.
Keywords:Kauffman Polynomial, Recurrence Relation, Generating Function

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
纽结(链环)多项式是一个纽结不变量,且是以系数符合给定纽结(链环)性质的多项式。其中重要的纽结多项式有:Alexander,Alexander-Conway,Jones多项式等,其均为定向纽结和链环的单变量Laurent多项式不变量。HOMFLY多项式是定向纽结和链环的双变量Laurent多项式不变量。Kauffman多项式F是纽结和链环的双变量的半定向多项式不变量,他可以更好地区分纽结(链环)和他的镜像。根据纽结或链环的Kauffman多项式F可以得出该纽结或链环的Jones多项式和BLM/Ho多项式等。Kauffman多项式F的原始版本是不定向纽结和链环图的正则合痕不变量,用L表示。
2014年,Berceanu B,Nizami A R利用简单递归关系,给出计算闭辫子Jones多项式的新方法,得出Jones多项式的一般展开式和有理生成函数 [1] 。2015年,Duzhin S,Shkolnikov M给出有理链环(纽结) HOMFLY多项式的详细公式 [2] 。Taşköprü K,Altıntaş İ研究了作为广义Fibonacci多项式的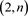 环面链环的HOMFLY多项式,给出
环面链环的HOMFLY多项式,给出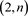 环面链环的HOMFLY多项式和广义的Fibonacci多项式之间的矩阵表示 [3] 。2018年,Ismet Altintas,Kemal Taşköprü,Merve Beyaztaş证明环面链环的尖括号多项式的递归关系式与Fibonacci多项式相似,给出其一些基本性质 [4] 。2019年,Altıntaş İ,Taşköprü K研究了可以作为Fibonacci类型多项式的
环面链环的HOMFLY多项式和广义的Fibonacci多项式之间的矩阵表示 [3] 。2018年,Ismet Altintas,Kemal Taşköprü,Merve Beyaztaş证明环面链环的尖括号多项式的递归关系式与Fibonacci多项式相似,给出其一些基本性质 [4] 。2019年,Altıntaş İ,Taşköprü K研究了可以作为Fibonacci类型多项式的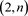 环面链环的Kauffman多项式和BLM\Ho多项式,借助BLM\Ho多项式来解释Kauffman多项式 [5] 。在此基础上,本文研究了一类n分支不定向直线型链环和复叠链环,并计算其Kauffman多项式。为实现此类链环Kauffman多项式的计算,第一部分介绍了纽结理论相关的基础知识和基本概念;第二部分计算n分支直线型链环的Kauffman多项式;第三部分借助n分支直线型链环的Kauffman多项式计算n分支复叠链环的Kauffman多项式。
环面链环的Kauffman多项式和BLM\Ho多项式,借助BLM\Ho多项式来解释Kauffman多项式 [5] 。在此基础上,本文研究了一类n分支不定向直线型链环和复叠链环,并计算其Kauffman多项式。为实现此类链环Kauffman多项式的计算,第一部分介绍了纽结理论相关的基础知识和基本概念;第二部分计算n分支直线型链环的Kauffman多项式;第三部分借助n分支直线型链环的Kauffman多项式计算n分支复叠链环的Kauffman多项式。
2. 预备知识
2.1. 纽结与链环
[6] 纽结:设K为S3中的一个简单闭曲线,且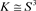 ,则称K为一个纽结,如果给定K一个定向,则称K为一个定向纽结。图1为平凡结。
,则称K为一个纽结,如果给定K一个定向,则称K为一个定向纽结。图1为平凡结。

Figure 1. Trivial knot
图1. 平凡结
[7] 链环:将若干个互不相交的圆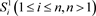 嵌入到三维欧氏空间R3中,这些圆形成的空间图称为链环,记
嵌入到三维欧氏空间R3中,这些圆形成的空间图称为链环,记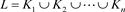 ,每个纽结
,每个纽结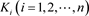 为链环L的一个分支,在此之中n为链环L的分支数。如果给每个链环的每一个分支一个固定的方向,则称这个链环为一个定向链环。
为链环L的一个分支,在此之中n为链环L的分支数。如果给每个链环的每一个分支一个固定的方向,则称这个链环为一个定向链环。
[6] 注1:纽结为分支数为1的链环。
[6] 注2:若链环L所有的分支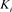 都是平凡结,则称链环L为平凡链环。如图2所示。
都是平凡结,则称链环L为平凡链环。如图2所示。
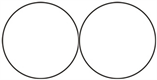
Figure 2. Trivial link
图2. 平凡链环
2.2. [8] 纽结(链环)的投影图
对于一个纽结(链环),选取一个合适的平面,选择一个合适的方向对其进行投影,把三维空间中的纽结(链环)正则投影到这个平面上,得到的投影图中只有有限多个交叉点;每个交叉点都是二重点,在上下线处的投影都是互相穿越交叉的。则称其为纽结(链环)投影图。
注:投影图会因为选取平面的不同而不同。
2.3. [9] [10] Reidemeister Move (R变换)
R变换是纽结理论中最基本的变换,它可以概括三维空间中纽结所有的拓扑情形。R变换是改变纽结的正则投影图的三种方式,其中每一种方式都会改变交叉点之间的关系。Reidemeister变换有三种变换方式,分别为R1变换、R2变换、R3变换。如图3所示。
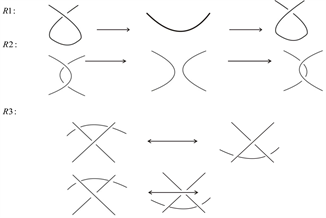
Figure 3. Reidemeister moves
图3. Reidemeister变换
2.4. [11] 纽结的分离并
在链环L的补空间 中,存在一个二维球面S,将其嵌入可以将链环L分为不同的连通分支,并且这两个分支分布在球面S的两侧,则称链环L为可分离的。如果将所得的这两个不同的连通分支记为
中,存在一个二维球面S,将其嵌入可以将链环L分为不同的连通分支,并且这两个分支分布在球面S的两侧,则称链环L为可分离的。如果将所得的这两个不同的连通分支记为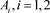 ,则此时
,则此时 ,称L为L1和L2的分离并,记作
,称L为L1和L2的分离并,记作 。
。
2.5. [5] Kauffman多项式 定义
定义
Kauffman多项式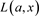 是不定向链环投影图K的一个双变量的Laurent多项式,Kauffman多项式
是不定向链环投影图K的一个双变量的Laurent多项式,Kauffman多项式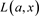 是链环K的合痕不变量。并且Kauffman多项式
是链环K的合痕不变量。并且Kauffman多项式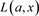 的特殊化是链环的尖括号多项式,其也是BLM/Ho多项式的双变量推广。
的特殊化是链环的尖括号多项式,其也是BLM/Ho多项式的双变量推广。
2.6. [5] Kauffman多项式 的计算满足如下几个规则
的计算满足如下几个规则
1) 
其中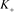 、
、 、
、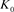 、
、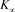 是如图4所示的不定向图。
是如图4所示的不定向图。
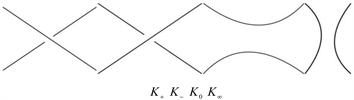
Figure 4. 、
、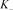 、
、 and
and 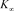
图4. 、
、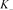 、
、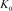 和
和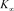
2) ,其中O为平凡结。
,其中O为平凡结。
3)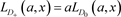 。
。
4) 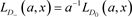
其中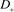 、
、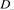 、
、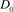 是如图5所示的不定向图。
是如图5所示的不定向图。
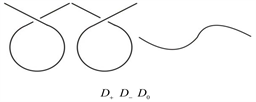
Figure 5.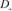 、
、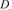 and
and 
图5.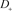 、
、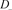 和
和
2.7. [5] Kauffman多项式 的性质
的性质
1)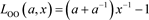 或
或 ,
, ,其中OO为2分支的平凡链环。
,其中OO为2分支的平凡链环。
2) 是一个平凡的m分支链环,
是一个平凡的m分支链环,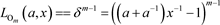 。
。
3)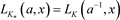 ,其中
,其中 表示链环K的镜像。
表示链环K的镜像。
4)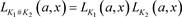 ,其中
,其中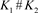 为链环
为链环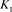 和
和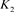 的组合。
的组合。
5)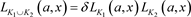 ,其中
,其中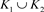 为链环
为链环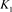 和
和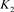 的不相交并。
的不相交并。
3. 一类特殊链环的Kauffman多项式L
n分支直线型链环Ln的Kauffman多项式L(Ln)
[11] 定义3.1 n分支直线型链环Ln:由n个分支所构成,且是由n个平凡结按照特定方式并在一起,如图6所示。
注1:最简单的非平凡的直线型链环为2个分支的直线型链环,即Hopf链环。
注2:规定1分支的直线型链环为平凡结。

Figure 6. Linear links Ln
图6. 直线型链环Ln
[12] 定义3.2 n分支复叠链环Kn:由n个分支构成,是由n个平凡结两两相扣所得。如图7所示。
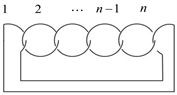
Figure 7. The covering links of n components link Kn
图7. n分支复叠链环Kn
定理3.1 n分支直线型链环Ln,其Kauffman多项式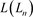 表达式为
表达式为
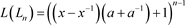 .
.
证明 对于n分支直线型链环Ln,对其左下角交叉点应用Kauffman多项式的拆接关系式,令其生成链环分别为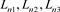 ,如图8所示。
,如图8所示。
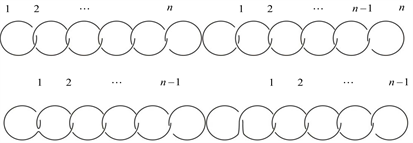
Figure 8. The skein relation of Ln
图8. Ln的拆接关系式
即拆接关系式为
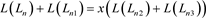 ,
,
其中链环 为平凡结与
为平凡结与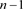 分支直线型链环
分支直线型链环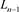 的并;对
的并;对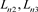 应用一系列R1变换得到链环
应用一系列R1变换得到链环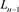 。可以得到如下关系式
。可以得到如下关系式
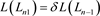 ,
,
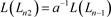 ,
,
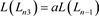 .
.
即拆接关系式等价于
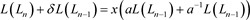 ,其中
,其中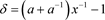
对其进行整理,得到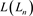 的递归关系式
的递归关系式
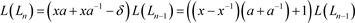 ,
,
则有
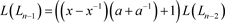 ,
,
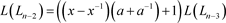 ,
,

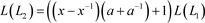
由于L1为1分支的直线型链环,为平凡结,则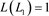 。
。
对上述等式进行合并整理,有
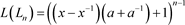 .
.
定理得证。
定理3.2 n分支复叠链环Kn的Kauffman多项式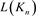 的递归关系式为
的递归关系式为
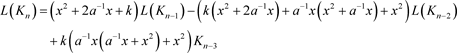
初值为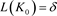 ,
,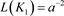 ,
,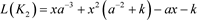 ,其中
,其中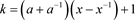 。
。
证明 下面对一类不定向n分支复叠链环Kn的Kauffman多项式进行研究,首先对链环Kn左上角的交叉点应用Kauffman多项式的拆接关系式,令其生成的三个链环分别为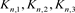 ,拆接关系式如图9所示。
,拆接关系式如图9所示。
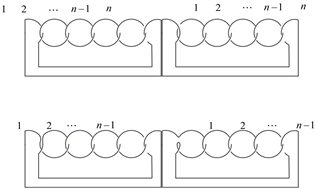
Figure 9. The skein relation of Kn
图9. Kn的拆接关系式
即拆接关系式为
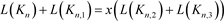 (3.1)
(3.1)
而对链环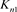 应用一系列R2变换,其可看作n分支直线型链环Ln;对链环
应用一系列R2变换,其可看作n分支直线型链环Ln;对链环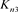 应用一系列R1变换,其可看作
应用一系列R1变换,其可看作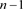 分支复叠链环
分支复叠链环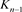 。
。
则3.1式等价于
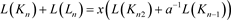 . (3.2)
. (3.2)
观察发现, 为
为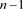 分支链环,令其为
分支链环,令其为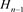 。接着对链环
。接着对链环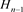 左上角的交叉点A应用Kauffman多项式的拆接关系式,令其所生成的链环分别为
左上角的交叉点A应用Kauffman多项式的拆接关系式,令其所生成的链环分别为 ,拆接关系如图10所示。
,拆接关系如图10所示。
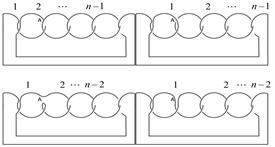
Figure 10. The skein relation of 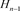
图10. 的拆接关系式
的拆接关系式
即拆接关系式为
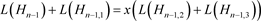 , (3.3)
, (3.3)
而对链环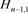 应用一系列R1、R2变换,其可看作
应用一系列R1、R2变换,其可看作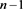 分支直线型链环
分支直线型链环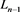 ;对链环
;对链环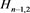 应用一系列R1变换,其可看作
应用一系列R1变换,其可看作 分支链环
分支链环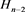 ;链环
;链环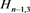 为
为 分支链环,令其为
分支链环,令其为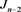 。
。
则3.3式等价于
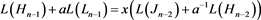 . (3.4)
. (3.4)
下面对 分支的链环
分支的链环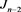 的Kauffman多项式进行研究,对链环
的Kauffman多项式进行研究,对链环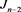 的交叉点B应用Kauffman多项式的拆接关系式,令其生成的链环分别为
的交叉点B应用Kauffman多项式的拆接关系式,令其生成的链环分别为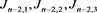 ,如图11所示。
,如图11所示。
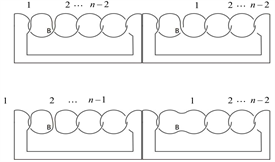
Figure 11. The skein relation of 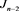
图11. 的拆接关系式
的拆接关系式
即拆接关系式为
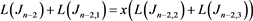 , (3.5)
, (3.5)
而对链环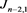 应用一系列R2变换,其可看作
应用一系列R2变换,其可看作 分支复叠链环
分支复叠链环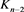 ;对链环
;对链环 应用一系列R1变换,其可看作
应用一系列R1变换,其可看作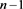 分支直线型链环
分支直线型链环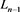 ;链环
;链环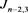 为
为 分支链环
分支链环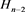 。
。
则3.5式等价于
 . (3.6)
. (3.6)
对3.2、3.4、3.6式进行合并、整理,可得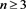 时,Kn的Kauffman多项式
时,Kn的Kauffman多项式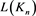 的递归关系式为:
的递归关系式为:
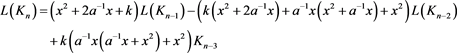 (3.7)
(3.7)
初值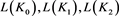 的计算分别如下:
的计算分别如下:
1) 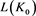
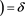

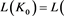 .
.
2) 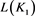
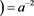
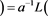
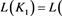 .
.
3) 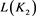
对链环K2的左上方的交叉点应用Kauffman多项式的拆接关系式,令生成的链环分别为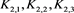 ,如图12所示。
,如图12所示。

Figure 12. The skein relation of K2
图12. K2的拆接关系式
则有如下表达式

而对链环 应用一系列R2变换,其可看作2分支直线型链环L2;对链环
应用一系列R2变换,其可看作2分支直线型链环L2;对链环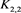 应用一系列R1变换,其可看作1分支链环L1。
应用一系列R1变换,其可看作1分支链环L1。
即
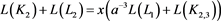 (3.8)
(3.8)
接着对链环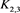 的右上方的交叉点应用Kauffman多项式的拆接关系式,令其生成的三个链环分别为
的右上方的交叉点应用Kauffman多项式的拆接关系式,令其生成的三个链环分别为 ,拆接关系式如图13所示。
,拆接关系式如图13所示。
则有
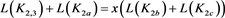
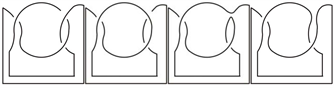
Figure 13. The skein relation of 
图13. 的拆接关系式
的拆接关系式
而对链环 应用一系列R1、R2变换,其可看作平凡结;对链环
应用一系列R1、R2变换,其可看作平凡结;对链环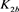 应用一系列R1变换,其可看作平凡结。即
应用一系列R1变换,其可看作平凡结。即
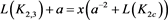 (3.9)
(3.9)
接着对链环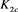 的左侧的交叉点应用Kauffman多项式的拆接关系式,令其生成的链环分别为
的左侧的交叉点应用Kauffman多项式的拆接关系式,令其生成的链环分别为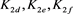 。如图14所示。
。如图14所示。
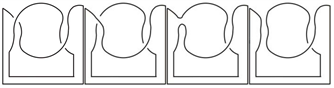
Figure 14. The skein relation of 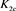
图14.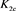 的拆接关系式
的拆接关系式
则有如下表达式
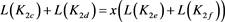
而对链环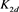 应用一系列R2变换,其可看作两个平凡结的并;对链环
应用一系列R2变换,其可看作两个平凡结的并;对链环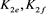 应用一系列R1变换,其可看作平凡结。即
应用一系列R1变换,其可看作平凡结。即
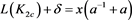 (3.10)
(3.10)
对3.8~3.10式进行合并整理,得到链环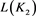 的表达式为:
的表达式为:
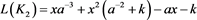
其中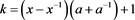 。
。
综上所述,定理得证。
注:全文k均为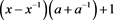 。
。
定理3.3 n分支复叠链环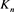 的Kauffman多项式
的Kauffman多项式 所对应特征多项式的特征根为
所对应特征多项式的特征根为
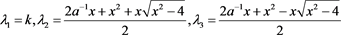
其中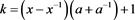
证明 由定理3.2可知,链环Kn的Kauffman多项式的递归关系式为
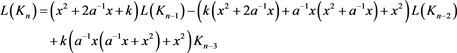
则其对应的特征多项式为
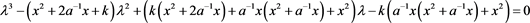
即
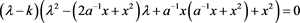
则该特征多项式的三个特征根分别为
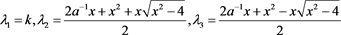 .
.
定理得证。
推论3.4 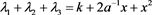
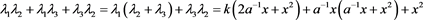
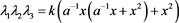
其中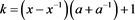
证明 将 、
、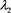 、
、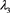 的值带入即可得到。
的值带入即可得到。
性质3.5 序列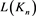 对应的生成函数为
对应的生成函数为
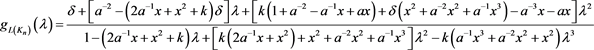
其中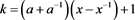 。
。
证明 的生成函数的形式如下:
的生成函数的形式如下:
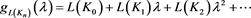
分别对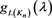 乘以
乘以
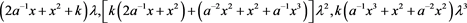
则有
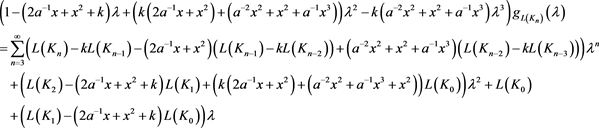
由序列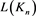 的递归关系式可知
的递归关系式可知
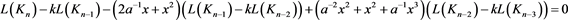 ,
,
则
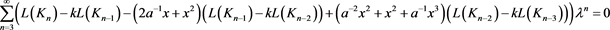
则原式等价于
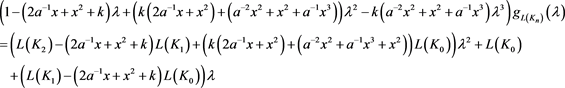
将三个初值 、
、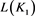 、
、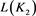 的值依次代入上述等式,即可得到序列
的值依次代入上述等式,即可得到序列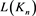 所对应的生成函数为
所对应的生成函数为
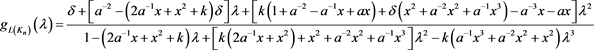
命题得证。
定理3.6 序列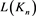 的通解为
的通解为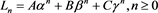 ,其中
,其中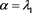 ,
,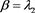 ,
,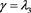
其中
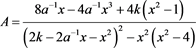

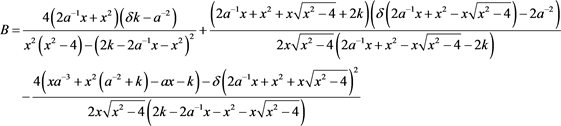
其中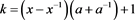
证明 序列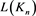 的通项公式为
的通项公式为
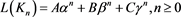
则分别令 ,有
,有
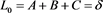 (1)
(1)
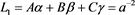 (2)
(2)
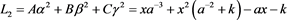 ,其中
,其中 . (3)
. (3)
解系数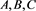 分别如下:
分别如下:
首先对系数C进行求解。对(1)式分别左右乘以 、
、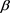 、
、 有(4)式,对(1)式分别左右乘以
有(4)式,对(1)式分别左右乘以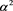 、
、 、
、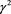 有(5)式。
有(5)式。
则有如下等式
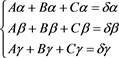 (4)
(4)
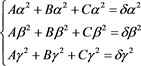 (5)
(5)
则将上述(4)、(5)两式分别与(2)、(3)式作差,有(6)式和(7)式:
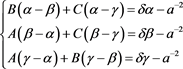 (6)
(6)
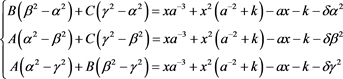 (7)
(7)
对上述(6)、(7)两式进行合并整理,得到C的表达式为:
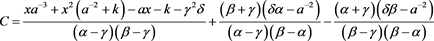
同理可以求出

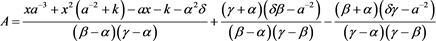
将 、
、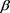 、
、 的值带入上述三个式子即可得到
的值带入上述三个式子即可得到
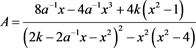
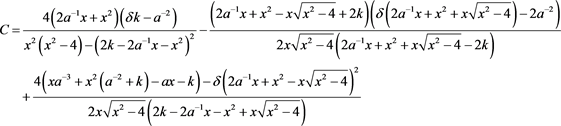

定理得证。
4. 结语
本文主要研究一类特殊不定向链环——复叠链环的Kauffman多项式。借助直线型链环的Kauffman多项式对复叠链环的Kauffman多项式进行研究。利用Kauffman多项式的拆接关系式推出其递归关系式,进而研究了这个递归关系式的生成函数。为研究定向复叠链环的Kauffman多项式以及BLM/Ho多项式奠定基础。
文章引用
徐芷微. 一类特殊链环的Kauffman多项式
The Kauffman Polynomials of a Special Class of Links[J]. 应用数学进展, 2023, 12(10): 4153-4165. https://doi.org/10.12677/AAM.2023.12100407
参考文献
- 1. Berceanu, B. and Nizami, A.R. (2014) A Recurrence Relation for the Jones Polynomial. Journal of the Korean Mathe-matical Society, 51, 443-462. https://doi.org/10.4134/JKMS.2014.51.3.443
- 2. Duzhin, S. and Shkolnikov, M. (2015) A Formula for the HOMFLY Polynomial of Rational Links. Arnold Mathematical Journal, 1, 345-359. https://doi.org/10.1007/s40598-015-0013-7
- 3. Taşköprü, K. and Altıntaş, İ. (2015) HOMFLY Polynomials of Torus Links as Generalized Fibonacci Polynomials. The Electronic Journal of Combinatorics, 22, P4.8. https://doi.org/10.37236/5324
- 4. Altıntas, I., Tasköprü, K. and Beyaztas, M. (2018) Bracket Polynomials of To-rus Links as Fibonacci Polynomials. International Journal of Advances in Applied Mathematics and Mechanics, 5, 35-43.
- 5. Altintas, I. and Takprü, K. (2019) Unoriented Knot Polynomials of Torus Links as Fibonacci-Type Polyno-mials. Asian-European Journal of Mathematics, 12, No. 4. https://doi.org/10.1142/S1793557119500530
- 6. (英)M. A. Armstrong. 基础拓扑学[M]. 北京: 人民邮电出版社, 2010.
- 7. 刘卫丽. 关于纽结的一个多项式不变量[D]: [硕士学位论文]. 大连: 大连理工大学, 2014.
- 8. Adams, C. (1994) The Knot Book. W.H. Freeman and Company, New York.
- 9. Adams C. (2004) The Knot Book. American Mathematical Society, New York.
- 10. Rolfsen, D. and Chelsea, A. (1976) Knots and Links. American Mathematical Society, New York.
- 11. 颜春惺. 一些定向链环的HOMFLY多项式[D]: [硕士学位论文]. 北京: 中国石油大学, 2021.
- 12. Alexander, J. W. (1928) Topological Invariants of Knots and Links. Transactions of the American Mathematical Society, 30, 275-306. https://doi.org/10.1090/S0002-9947-1928-1501429-1