International Journal of Mechanics Research
Vol.06 No.01(2017), Article ID:20035,13
pages
10.12677/IJM.2017.61004
Overview—Cell Migration Models
Jiju Feng, Liqun Tang*, Zejia Liu
School of Civil Engineering and Transportation, South China University of Technology, Guangzhou Guangdong

Received: Mar. 9th, 2017; accepted: Mar. 23rd, 2017; published: Mar. 30th, 2017

ABSTRACT
Cell migration occurred along with the whole life process of biology, both the embryonic development and disease are inseparable from the cell migration. In addition, cell migration model also can assist the experimental verification. Therefore, the cell migration and the related model play an important role in the analysis of various cell behaviors. In this paper, we introduce a comprehensive review of research on cell migration, which includes the forms of cell migration, cell model and various models of cell migration. There are some summary and discussion on the advantages and disadvantages of models in the domestic and foreign research on cell migration.
Keywords:Cell Migration, Model, External Source, Pseudopod
细胞迁移模型综述
冯继菊,汤立群*,刘泽佳
华南理工大学土木与交通学院工程力学系,广东 广州

收稿日期:2017年3月9日;录用日期:2017年3月23日;发布日期:2017年3月30日

摘 要
细胞迁移的发生伴随着生物体整个生命过程,无论是胚胎的发育,还是疾病的发生都离不开细胞的迁移;且细胞迁移模型的建立也可以辅助实验验证,因此细胞迁移模型在分析细胞迁移行为过程中起到重要作用。本文在前人的基础上综合介绍了国内外细胞力学中关于细胞迁移的力学研究,阐述细胞迁移过程涉及的力学模型方面,包括细胞迁移形式、细胞模型以及各种细胞迁移模型。文章综述和探讨了各种模型的优缺点,并对国内外研究细胞迁移模型的研究进程进行总结以及展望和探究。
关键词 :细胞迁移,模型,外界源,伪足

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
作为生命的基本单元,细胞是一个需要结合各种方法来理解的复杂生物系统,其中细胞力学的发展对其理解越来越重要 。活细胞能够感应机械力并将其转化为生物学响应 [1] 。机械力被认为是细胞功能的主要调节者,细胞的力学性能对细胞感应力、将力传递到细胞内部或者其他细胞、以及转换成化学信等的机制是必不可少的 [2] 。细胞力学的研究主要集中在细胞-力的感应传导 [3] 、细胞变形分析 [4] 、细胞骨架的力学特性 [5] 、细胞内外各种相关蛋白对调节和控制细胞变形运动的分子层面的作用 [6] [7] [8] [9] 及细胞在细胞外基质纤维ECM中的迁移运动等 [10] [11] [12] [13] 。
因为细胞迁移是细胞生物学的一个基本的现象,对器官、神经以及原胚肠等形态发生至关重要 [14] ,且细胞的迁移机制对癌细胞的扩散十分关键。目前恶性肿瘤的治疗仍然是生命科学界的一道难题,因为细胞迁移是癌细胞侵袭的一个基本方面,对抗和治疗癌症的手段主要在于确定和调节癌细胞迁移的主要因素,不仅要考虑分子层面的生物化学作用,也要考虑其力学调控机理。所以细胞迁移的力学研究就尤为突出和重要。
在研究细胞迁移的过程中发现,细胞突出(亦叫伪足)的形成是其必不可少的步骤,而突出的形成主要依靠肌动蛋白的流动或者肌动蛋白纤维的聚合,以及细胞骨架的收缩、钙离子的浓度和Rho GTP酶等的综合作用 [15] 。而不同的细胞迁移模式对应各种各样的伪足类型,例如由肌动蛋白聚合驱使形成的板状伪足和由肌球蛋白收缩产生内压导致气泡伪足的形成分别适用于不同的迁移模式 [16] [17] 等。伪足的形成使细胞在ECM中的迁移更容易和方便,对于细胞的扩散也有一定作用。所以研究细胞在不同环境中的迁移模式变化对理解细胞迁移机制十分重要,且迁移模型的建立有助于理解实验观测中无法解释的现象。
2. 细胞迁移的模式
在真核生物体内,除了基因表达、胞外离子浓度调节和酶的控制,细胞会通过不同的迁移形式穿过ECM到达目的地。细胞形状的可塑性和突出的多样性能够使细胞根据环境调整迁移模式以支持癌细胞扩散 [18] [19] [20] 。且癌细胞在体内的入侵、转移和扩散都会依赖周围的组织环境和信号调节来确定迁移模式,依据细胞伸出突出的形状及与ECM结构接触粘性特点可分为两大类迁移模式,即间充质细胞迁移模式和阿米巴细胞迁移模式 [19] ,如图1。
2.1. 间充质细胞迁移模式
如图1左所示为三维ECM中间充质细胞迁移模式的形态。研究发现细胞内的Rac GTPase和Rho两种分子是决定细胞在不同环境中适应于不同迁移模式的主要因素 [20] [21] ,其中当Rac1活性度较高时,调节肌动蛋白聚合使细胞以间充质细胞迁移模式形态迁移 [22] 。无论是在有机体内外都可以观察到符合此迁移模式的细胞表面有由肌动蛋白纤维聚合产生的片状或纺锤丝状的细胞膜突出(即片状或丝状伪

Figure 1. Two patterns of cell migration [18]
图1. 细胞迁移两种形式 [18]
足) [23] 。此模式通过前端伸出突出、局部形成黏着斑、周围水解纤维、胞体收缩和后端分离这五步完成一个迁移循环 [19] 。研究发现间充质细胞迁移模式区别于阿米巴迁移模式的特征主要在三个方面,即有黏着斑的形成、存在应力纤维和水解酶的作用 [19] ,而这些特点在阿米巴细胞迁移过程中不明显或完全没有。
首先,对癌细胞的研究发现细胞的粘性和ECM刚度变化会影响细胞的迁移状态 [22] [24] [25] ,而间充质细胞迁移过程中接触纤维需要很强的粘性力 [19] ,所以这种迁移模式通过整合素与ECM结合形成局部黏着斑,且主要适用于体型较大的粘附细胞,如平滑肌细胞 [22] 、纤维母细胞 [18] 及胶质瘤[26]等,所以间充质细胞迁移模式的速度较低 [19] ;其次,由细胞体的收缩和对ECM的锚固,交联蛋白将肌动蛋白纤维中的粗纤维进行了高度组织化的并联排列,产生应力纤维协助迁移 [19] [27] ;最后,在通过观察迁移过程发现细胞周围存在大量的水解酶,细胞分泌水解蛋白酶水解阻碍迁移的ECM纤维,并分泌相关因子促使纤维能够重组使自身能够顺利通过障碍进行迁移 [11] 。
通过细胞内部信号作用使得肌动蛋白纤维聚合产生片状或丝状伪足,结合整合素与ECM形成局部黏着斑和应力纤维,以及外部水解蛋白酶作用导致的纤维水解和重组,使得细胞以间充质细胞迁移模式进行迁移。这些特征可以明显的区别间充质细胞迁移模式,但是此种迁移模式涉及较多的化学分子,比如酶、整合素等,很难模拟出相对精确的力学平衡方程。
2.2. 阿米巴细胞迁移模式
如图1右为三维ECM中阿米巴细胞迁移模式的形态。研究发现当细胞内Rho分子浓度较高时,细胞皮质层的收缩性提高,进而引发整个胞体的收缩,同时肌动球蛋白的收缩导致肌动蛋白皮层断裂,使细胞质流出胞体填充细胞膜即形成气泡伪足,使细胞以阿米巴细胞迁移模式进行迁移 [22] [28] 。实验观察阿米巴细胞迁移模式中细胞会形成一个或多个气泡伪足辅助迁移 [29] [30] [31] 。
阿米巴细胞迁移过程主要通过四步循环,分别是皮质层断裂(或细胞膜与皮质的分离)、细胞质流动形成气泡、皮层愈合后与细胞膜相连(或皮层与细胞膜相连)、胞体的收缩 [17] [31] [32] 。阿米巴细胞迁移模式区别于其他迁移模式具有四个明显的特征:气泡形成过程中无肌动蛋白纤维聚合、细胞与ECM接触无局部黏着斑形成、高度变形速度非常快、不存在独特的水解和基质重组。
首先阿米巴细胞迁移模式主要依靠伸出的气泡带动胞体的整体前进,而决定气泡生长的主要因素是胞内信号引起的内压变化,在胞内显著缺乏肌动蛋白层和肌动蛋白纤维聚合的情况下,气泡能够驱使细胞发生迁移 [28] [31] [33] ;第二,胞内信号和细胞质的流动对气泡的生长至关重要,由于缺乏整合素受体,所以局部黏着斑的形成受限,对ECM的牵引力和细胞黏性要求很小 [19] 。因此迁移模式适用于体型较小类似于球体或椭球体的悬浮细胞,如T淋巴癌细胞、肺癌细胞 [34] 、白细胞 [35] 等,所以其速度是间充质模式的10~30倍 [19] ;最后可根据迁移过程中是否有水解酶来判断是否符合此迁移模式 [36] ,由于细胞膜缺乏相关水解酶,故而没有水解现象和基质重组。
阿米巴细胞迁移模式中因缺少肌动蛋白的聚合,故细胞能够消耗很少的能量到达目的地 [31] ,且因伸出的气泡具有较好的弹性和可塑性,所以细胞能够入侵ECM中很小的空间 [14] ,其速度更快、方向更准确 [37] 。此迁移模式主要依靠细胞膜的力学特性,通过内部信号、细胞膜、皮质层及细胞质的相互耦合作用,及气泡伪足探索,结合少量ECM纤维作用来完成迁移过程。
3. 细胞迁移力学模型
无论是间充质细胞迁移还是阿米巴细胞迁移模式,在细胞实验研究中,都需要相关理论来解释实验现象。细胞模型和细胞迁移模型的建立不仅可以对细胞迁移实验现象进行合理解释,也可以对细胞在外界荷载作用下的复杂力学响应进行分析。近几十年来对细胞的力学实验研究发现,细胞迁移的能力与细胞的主动和被动变形紧密相关 [38] [39] [40] 。近年来,国内外对细胞迁移迁移研究主要以两方面出发,细胞模型 [41] [42] 和细胞迁移模型 [43] [44] [45] 。
3.1. 细胞模型
细胞模型发展通过用不同的实验方法和在已有模型基础上演化,建立新的更有意义的能解决更多实际问题的细胞模型,其中实验方法包括:试管吸入细胞实验和磁扭转血细胞计数MTC和原子力显微技术AFM等;模型演化包括使用Gibson等人 [46] 提出的多胞材料模型、Ingber等人 [47] [48] 骨架结构模型及基于单个活细胞骨架纤维的超微结构观测和力学测量的基础上提出固体模型。
在细胞模型发展和完善过程中,试管吸入实验起重要的验证作用 [41] [49] 。如图2,通过实验观察可将细胞看作不同材料相组成的共同体。细胞模型可分为单一相介质、固液相结合介质,其中单一相有固体模型,固液两相模型以及采用MTC及AFM技术得到的频域模型。
3.1.1. 固体模型
固体模型包含将细胞看成整体的弹性固体模型和只考虑细胞骨架作用的细胞骨架网络模型。
前者将细胞简化成均匀的各向同性固体、忽略细胞各层区别及相互作用,将细胞看作是不可压缩的线弹性或粘弹性固体,由一个Maxwell模型和弹簧串联而成 [50] [51] 。此粘弹性固体模型解决了细胞的微小应变和变形状态,但不能完全解释细胞的吸入行为;后者将细胞的骨架作为细胞整体结构响应,提出三种骨架网络模型:胞元模型 [52] 、张力整合模型 [53] [54] 和绳索网络模型 [55] 。这些模型有各自的适用范围 [56] - [65] 。
3.1.2. 固液两相模型
由固、液相结合的模型包括将细胞看成是由连续皮层包围的球形液滴模型 [41] [49] [66] [67] [68] [69] 和分别将细胞内固相和液相区分考虑的两相模型 [70] 。
前者主要用于模拟悬浮细胞,解释细胞在微吸管实验中的流变性质,包括由各向异性的粘性流体皮层包围的均匀牛顿粘性流体的牛顿流体液滴模型 [41] [49] 、包含一定厚度的细胞膜、类液体的细胞内质和

Figure 2. A test-tube experiments [37]
图2. 试管实验 [37]
和骨架环绕的细胞核组成的复合牛顿流体液滴模型 [66] [67] 、细胞质粘性对剪切速率的剪切稀化液滴模型 [68] 和由含有预应力的皮层壳包围Maxwell液体的液滴模型 [69] 。两相模型区分对待细胞质中的固体聚合物和液态间质 [70] ,将固相假设成线弹性材料(占细胞体积约20%)、液相假设为无粘性液体(占细胞体积约80%)且可以透过固相扩散 [71] [72] 。
3.1.3. 频域模型
振荡型MTC技术及AFM技术的提出主要因为实际生理环境中很多种类的细胞都会受到动态作用力,于是发展了与之前模型完全不同的频域模型 [73] [74] [75] [76] 。使用振荡型MTC及AFM实验,将磁珠嵌入细胞表面,其嵌入深度决定了磁珠扭转位移,通过改变加入的磁场大小来决定珠子的转动和平移,发现细胞动态储能模量与磁场振荡频率之间存在弱幂级数关系,于是就提出了指数定律结构阻尼模型来描述细胞的流变学行为,主要用于解释贴壁细胞的动态行为 [76] ,并结合三维有限元来解决MTC实验中细胞变形形状和应力应变问题 [77] 。
3.2. 细胞迁移模型
细胞迁移是指在持续的力学刺激下,细胞发生形态学改变、表面受体蛋白重新分布,引起一系列化学变化和信号传导,这些级联反应引起细胞形态学上的进一步变化,如极化、突起、黏附,最终导致细胞的迁移运动 [43] [44] [45] [78] 。细胞的迁移运动既需要细胞内外信号源的刺激和调节控制 [44] ,也需要不同类型的伪足协助。结合细胞的趋性特征,加上伪足的调节使不同的迁移模式更顺利 [79] 。而伪足的类型主要由细胞与ECM相互作用决定,主要包括四种类型:丝状伪足、板状伪足、气泡和侵入性伪足 [16] ,如图3。细胞对药物 [80] [81] [82] [83] [84] 、热 [85] 、电场 [86] 等外界源的趋性使其迁移更容易发生。在内外信号和伪足的作用下,由细胞两种迁移模式衍生了很多细胞迁移模型。
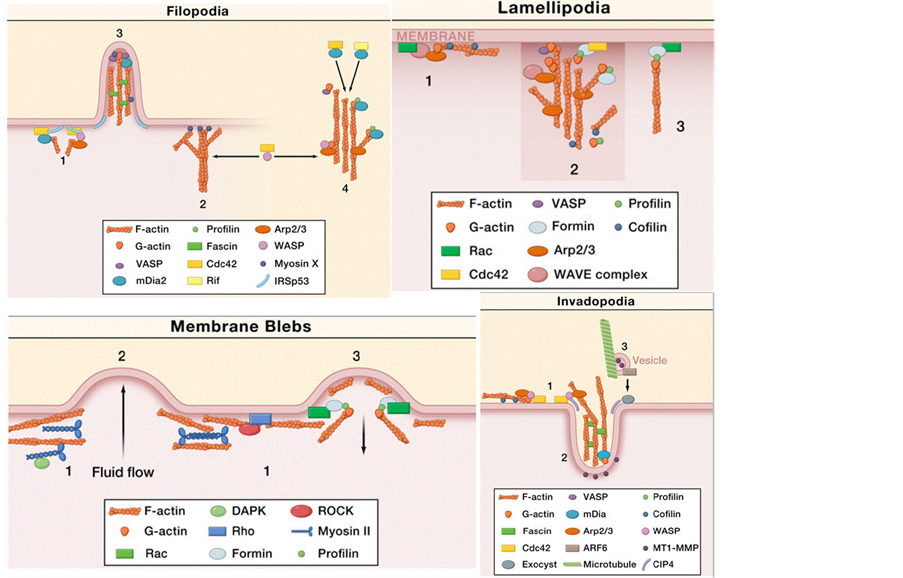
Figure 3. Four types of pseudopod [16]
图3. 伪足四种类型 [16]
模型考虑的源信号包括细胞与ECM结构的内部信号和施加于细胞与ECM结构外界信号。内部信号源有细胞表面受体浓度、ECM中配体浓度、基质刚度;外界信号源有化学引诱物、电场、温度等。也会考虑是否有伪足参与迁移过程来划分迁移模型。
3.2.1. 受内部源影响的无伪足细胞迁移模型
当细胞迁移仅受内部源,即细胞表面受体和基质中的配体浓度的影响时,Zaman等人 [87] 建立一个三维的无外源刺激的随机细胞模型,模型为忽略细胞内部肌动蛋白纤维聚合作用、基质中金属蛋白酶水解对受体和配体作用的小球。在受配体结合形成的粘性过高或过低影响下,细胞速度都很小;在适合的粘性中,细胞速度呈正相关,但是细胞的迁移轨迹表现随机,没有目标性。此模拟了间充质细胞迁移模式中黏着斑的形成及对细胞迁移的作用和影响,但忽略了间充质细胞迁移模式的其他主要特征。
Dokukina等人 [88] 提出符合间充质细胞迁移模式的二维的离散骨架模型,在改变基质的杨氏模量情况下观察细胞的运动轨迹,发现当细胞从软基底迁移到硬基底时,其所受牵引力、速度和面积全部增加;反之,细胞会改变迁移轨迹避开软基底。这种现象与间充质细胞迁移形态的实验现象几近一致 [89] [90] 。但由弹性杆件组成的模型结构单一,忽略细胞与ECM大部分力学特性,并没有表达间充质细胞迁移模式的力学特征。
于是Wong等人 [91] 提出三维包含基质降解、受配体浓度变化的细胞与ECM相互作用模型。模型考虑细胞在不同受配体浓度梯度中的迁移问题,不足是模型将细胞与ECM作为整体建模,忽略细胞的分层结构和内部肌动蛋白纤维作用,但模型却充分反映了间充质细胞迁移模式中黏着斑和水解这两个主要特征,并进一步模拟和探讨了这种模式的迁移速度、作用力等力学特征,具有一定的参考价值。
细胞在无外界源作用和伪足参与时也能自发的发生迁移运动,是因为细胞内部分子的调控机制,及ECM中基质浓度、弹性模量变化等的辅助。这三种无外源无伪足的细胞迁移模型都反映了间充质细胞迁移模式的部分特点,忽略了肌动蛋白纤维聚合作用。
3.2.2. 受外界源影响的无伪足细胞迁移模型
当有外界源作用时,研究者建立了几种有外界源影响的无伪足细胞迁移模型。外界源包括化学物质、电场和温度场等,如常用化学物质有磷脂酰肌醇-3羟基酶、物质环磷酸腺苷等 [80] 、细胞最合适的电压介于40~180 mV/mm之间 [86] 、细胞对温度在29-41℃之间较为敏感 [85] 等。不同类型的外界源对细胞迁移的影响是不一样的。
Mousavi等人 [92] [93] 发展了一种受内外因子作用的三维细胞模型,如图4。模型将细胞看成在牛顿纤维胶介质中的球,ECM是线粘弹性介质;模型考虑结构内部的肌动蛋白纤维聚合、肌球蛋白收缩、基
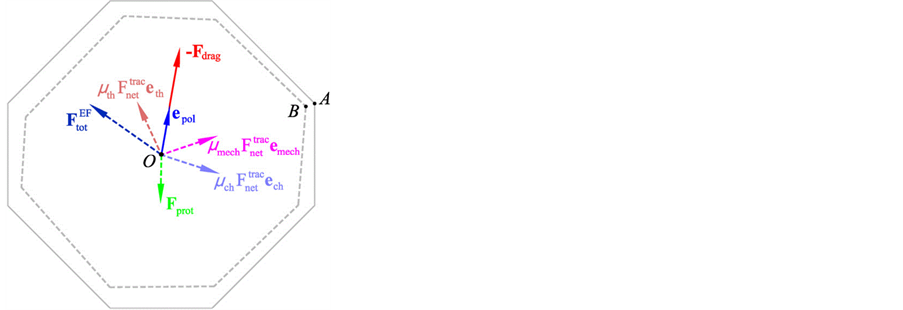
Figure 4. The three-dimensional sensing model [80] [81]
图4. 三维感应模型 [80] [81]
质刚度变化,外部的源信号有机械力、化学离子、温度场和电场的作用。完整的解释了细胞在三维环境中应力分布、源对运动轨迹的影响,反应了细胞骨架对细胞收缩的影响和细胞的趋性特点,与实验结果相差无几 [94] [95] [96] 。此模型对间充质细胞迁移模式中的肌动蛋白纤维聚合现象进行合理的模拟,但对于黏着斑、应力纤维和水解等主要特征并没有模拟。
而Yang等人 [97] [98] 结合人工智能机器人对符合阿米巴细胞迁移模式的T淋巴细胞的迁移现象进行实验研究,给出在有化学引诱物刺激作用下的三维细胞数学模型,主要分析不同浓度的化学引诱物对细胞迁移的影响。模型考虑了细胞配体浓度变化、肌动蛋白聚合、分子马达等的作用力,但是缺少对阿米巴细胞迁移模式特征的表达和模拟,没有突出在外界源信号中阿米巴细胞迁移模式的形态和特点。
3.2.3. 受外界源影响的有伪足细胞迁移模型
不同类型的细胞,在源信号刺激下根据不同环境下伸出不同类型的伪足,细胞就会产生不同的迁移模式,从而对应不同的迁移模型。
Van Haastert等人 [99] 对符合阿米巴细胞迁移模式的细胞在有源信号时进行试验,并建立二维有伪足的细胞迁移数学模型 [83] 。实验指出当存在化学引诱物时,细胞会生成朝向源信号生长和爬行的伪足,如图5在引诱物梯度控制下,细胞迁移形态变化。模型虽然合理解释源信号、伪足与迁移之间的相互联系和作用,但忽略了细胞固有的力学属性,且没有模拟阿米巴细胞迁移模式的气泡伪足,及对无黏着斑形成和无水解现象的解释。
而Lim等人 [23] 针对阿米巴细胞迁移模式提出二维的数学模型,在机械信号作用下模拟气泡伪足对迁移的作用,明确提出了模型中无黏着斑形成和水解现象,合理解释了阿米巴细胞迁移模式的主要特征。但是模型忽略细胞核,结构单一,气泡的生成方式主要依靠外界施加作用力,没有将细胞自身的生化机

Figure 5. The track of pseudopod sprout [87]
图5. 伪足生长轨迹 [87]
制转化为力学作用。
Allena R [100] [101] 综合外界源信号强度作用,建立三维细胞与伪足模型。模型考虑胞内肌动蛋白纤维粘弹性作用、混在细胞液中的细胞器的黏性作用以及细胞质的流体作用。模型模拟了由肌动蛋白纤维聚合引起的片状或丝状伪足的生成状态、个数和应力状态等,如图6。模型中细胞质、肌动蛋白网络和伪足被分成不同的区域,简化了交互过程,充分展现了间充质细胞迁移模式的伪足生成过程的状态,但同时也忽略了细胞结构各层之间的相互作用,以及黏着斑和水解现象的模拟。
目前为止,对外界源信号作用于细胞迁移的研究主要集在化学物质的作用,对于其他外界源信号,比如电场和温度场等的研究较少,相对应的细胞迁移模型则很少。这三种受外界源信号作用的有伪足伸出的细胞迁移模型主要表达了细胞的两种迁移模式下伸出伪足的不同,包括其生成原因、状态和结构;但是没有表达其它能够区别两种迁移模式的主要特征。
4. 总结与展望
文章对国内外细胞力学关于迁移模型方面的具体研究进行总结和回顾,从实验观察得到细胞迁移的两种模式,然后根据不同类型的细胞的不同的迁移方式,衍生出不同的细胞模型和细胞迁移模型。这些模型为研究细胞迁移提供合理的理论方法,对理解细胞内部的力学特性、变形特征以及迁移特点都必不可少,且将细胞内部的信号机制、ECM结构变化、外界源以及伪足的作用充分展示出来,使我们对细胞
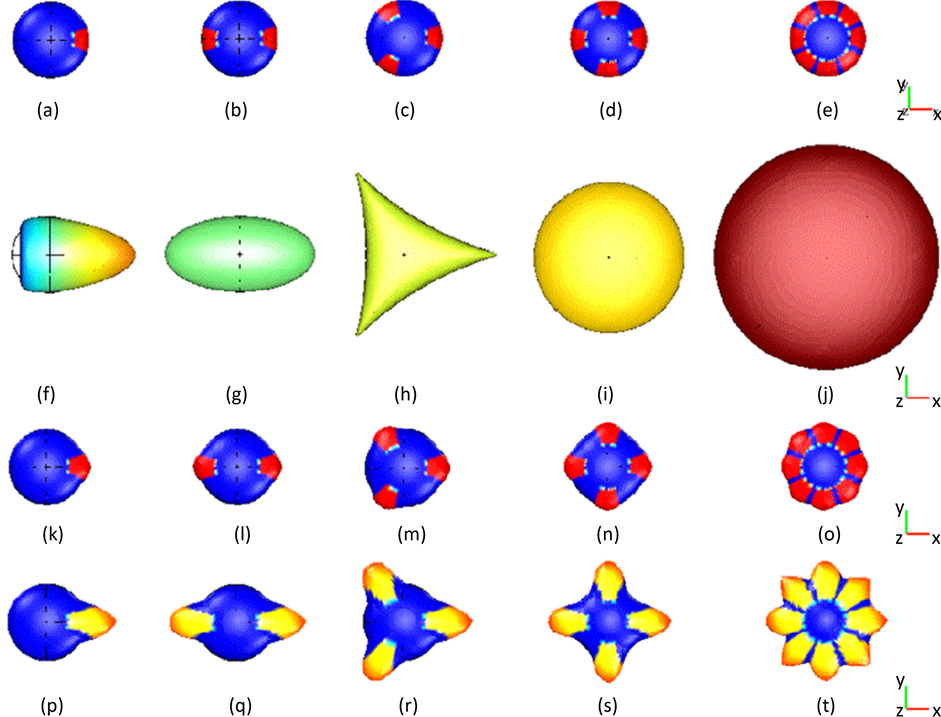
Figure 6. The process of pseudopod morphology variation [88]
图6. 伪足形态变化过程[88]
迁移系统有更深刻的理解和认识。
但已有的模型并不是很完善和统一。细胞模型忽略了细胞内部复杂的多相结构,使用较多的力学假设和简化,不能完整展示细胞的力学特性。三类细胞迁移模型分别反应了在内部信号作用下间充质细胞迁移模式的水解现象或黏着斑形成、在外界源影响时无伪足生出情况下,细胞两种迁移模式的达到迁移条件的区别,及在考虑内外因素和伪足作用下的两种细胞迁移模式的形态特征和区别;但这三类迁移模型分别忽略了肌动蛋白纤维聚合作用和应力纤维的存在、肌动蛋白聚合形成的伪足的不同机制之间的转换和模型完整的完整性。
为了解决这些模型存在的问题,需要考虑细胞的多相结构的耦合,考虑细胞的主动迁移机制,纤维的作用以及伪足在迁移中的作用表达等。细胞迁移模型的发展,使我们对微结构或超微结构的细胞或细胞组分更进一步理解,能够精确探测细胞各个部位的作用力和位移,并能够对细胞施加定向作用力,以找到能够抑制特定细胞迁移的方法,达到解决癌细胞扩散的目的。
基金项目
国家自然科学基金(11472109)。
文章引用
冯继菊,汤立群,刘泽佳. 细胞迁移模型综述
Overview—Cell Migration Models[J]. 力学研究, 2017, 06(01): 24-36. http://dx.doi.org/10.12677/IJM.2017.61004
参考文献 (References)
- 1. Bao, G. and Suresh, S. (2003) Cell and Molecular Mechanics of Biological Materials. Nature Materials, 2, 715-725. https://doi.org/10.1038/nmat1001
- 2. Janmey, P.A. and Mcculloch, C.A. (2007) Cell Mechanics: Integrating Cell Responses to Mechanical Stimuli. Annual Review of Biomedical Engineering, 9, 1-34. https://doi.org/10.1146/annurev.bioeng.9.060906.151927
- 3. Borau, C., Kamm, R.D. and Garcia-Aznar, J.M. (2011) Mechano-Sensing and Cell Migration: A 3D Model Approach. Physical Biology, 8, 1-13. https://doi.org/10.1088/1478-3975/8/6/066008
- 4. Karcher, H., Lammerding, J., Huang, H.D., et al. (2003) A Three-Dimensional Viscoelastic Model for Cell Deformation with Experimental Verification. Biophysical. Journal, 85, 3336-3349. https://doi.org/10.1016/S0006-3495(03)74753-5
- 5. Fletcher, D.A. and Mullins, D. (2010) Cell Mechanics and the Cytoskeleton. Nature, 463, 485-492. https://doi.org/10.1038/nature08908
- 6. Cukierman, E., Pankov, R., Stevens, D.R., et al. (2001) Taking Cell-Matrix Adhesions to the Third Dimension. Science, 294, 1708-1712. https://doi.org/10.1126/science.1064829
- 7. Giannone, G., Dubin-Thaler, B.J., Rossier, O., et al. (2007) Lamellipodial Actin Mechanically Links Myosin Activity with Adhesion-Site Formation. Cell, 128, 561-575. https://doi.org/10.1016/j.cell.2006.12.039
- 8. Qian, J., Wang, J. and Gao, H. (2008) Lifetime and Strength of Adhesive Molecular Bond Clusters between Elastic Media. Langmuir, 24, 1262-1270. https://doi.org/10.1021/la702401b
- 9. Belletti, B., Nicoloso, M.S., Schiappacassi, M., et al. (2008) Stathmin Activity Influences Sarcoma Cell Shape, Motility, and Metastatic Potential. Molecular Biology of the Cell, 19, 2003-2013. https://doi.org/10.1091/mbc.E07-09-0894
- 10. Friedl, P., Zanker, K.S. and Brocker, E.B. (1998) Cell Migration Strategies in 3D Extracellular Matrix: Differences in Morphology, Cell Matrix Interactions, and Integrin Function. Microscopy Research and Technique, 43, 369-378. https://doi.org/10.1002/(SICI)1097-0029(19981201)43:5<369::AID-JEMT3>3.0.CO;2-6
- 11. Even-Ram, S. and Yamada, K.M. (2005) Cell Migration in 3D Matrix. Current Opinion in Cell Biology, 17, 524-532. https://doi.org/10.1016/j.ceb.2005.08.015
- 12. Friedl, P. and Gilmour, D. (2009) Collective Cell Migration in Morphogenesis, Regeneration and Cancer. Nature Reviews Molecular Cell Biology, 10, 445-457. https://doi.org/10.1038/nrm2720
- 13. Wolf, K. and Friedl, P. (2009) Mapping Proteolytic Cancer Cell-Extracellular Matrix Interfaces. Clinical & Experimental Metastasis, 26, 289-298. https://doi.org/10.1007/s10585-008-9190-2
- 14. Tsujioka, M. (2011) Cell Migration in Multicellular Environments. Development, Growth & Differentiation, 53, 528- 537. https://doi.org/10.1111/j.1440-169X.2011.01268.x
- 15. Blaser, H., Reichman-Fried, M., Castanon, I., et al. (2006) Migration of Zebra Fish Primordial Germ Cells: A Role for Myosin Contraction and Cytoplasmic Flow. Developmental Cell, 11, 613-627. https://doi.org/10.1016/j.devcel.2006.09.023
- 16. Ridley, A.J. (2011) Life at the Leading Edge. Cell, 145, 1012-1022. https://doi.org/10.1016/j.cell.2011.06.010
- 17. Charras, G. and Paluch, E. (2008) Blebs Lead the Way: How to Migrate without Lamellipodia. Nature Reviews Molecular Cell Biology, 9, 730-736. https://doi.org/10.1038/nrm2453
- 18. Wolf, K., Mazo, I., Leung, H., et al. (2003) Compensation Mechanism in Tumor Cell Migration: Mesenchymal-Amoeboid Transition after Blocking of Pericellular Proteolysis. The Journal of Cell Biology, 160, 267-277. https://doi.org/10.1083/jcb.200209006
- 19. Friedl, P. and Wolf, K. (2003) Tumour-Cell Invasion and Migration: Diversity and Escape Mechanisms. Nature Reviews Cancer, 3, 362-374. https://doi.org/10.1038/nrc1075
- 20. Sanz-Moreno, V. and Marshall, C.J. (2010) The Plasticity of Cytoskeletal Dy-namics Underlying Neoplastic Cell Migration. Current Opinion in Cell Biology, 22, 690-696. https://doi.org/10.1016/j.ceb.2010.08.020
- 21. Friedl, P. and Wolf, K. (2010) Plasticity of Cell Migration: A Multiscale Tuning Model. The Journal of Cell Biology, 188, 11-19. https://doi.org/10.1083/jcb.200909003
- 22. Bergert, M., Chandradoss, S.D., Desai, R.A., et al. (2012) Cell Mechanics Control Rapid Transitions between Blebs and Lamellipodia during Migration. Proceedings of the National Academy of Sciences of the United States of America, 109, 14434-14439. https://doi.org/10.1073/pnas.1207968109
- 23. Lim, F.Y., Koon, Y.L. and Chiam, K.H. (2013) A Computational Model of Amoeboid Cell Migration. Computer Methods in Biomechanics and Biomedical Engineering, 16, 1085-1095. https://doi.org/10.1080/10255842.2012.757598
- 24. Lammermann, T. and Sixt, M. (2009) Mechanical Modes of “Amoeboid” Cell Migration. Current Opinion in Cell Biology, 21, 636-644. https://doi.org/10.1016/j.ceb.2009.05.003
- 25. Barnhart, E.L., Lee, K.C., Keren, K., et al. (2011) An Adhe-sion-Dependent Switch between Mechanisms That Determine Motile Cell Shape. PLOS Biology, 9, 19. https://doi.org/10.1371/journal.pbio.1001059
- 26. Paulus, W., Baur, I., Beutler, A.S., et al. (1996) Diffuse Brain Invasion of Glioma Cells Requires Beta 1 Integrins. Laboratory Investigation: A Journal of Technical Methods and Pathology, 75, 819-826.
- 27. Shao, D.Y., Levine, H. and Rappel, W.J. (2012) Coupling Actin Flow, Adhesion, and Morphology in a Computational Cell Motility Model. Proceedings of the National Academy of Sciences of the United States of America, 109, 6851- 6856. https://doi.org/10.1073/pnas.1203252109
- 28. Paluch, E., Sykes, C., Prost, J., et al. (2006) Dynamic Modes of the Cortical Actomyosin Gel during Cell Locomotion and Division. Trends in Cell Biology, 16, 5-10. https://doi.org/10.1016/j.tcb.2005.11.003
- 29. Charras, G.T., Hu, C.-K., Coughlin, M., et al. (2006) Reassembly of Contractile Actin Cortex in Cell Blebs. The Journal of Cell Biology, 175, 477-490. https://doi.org/10.1083/jcb.200602085
- 30. Charras, G.T., Coughlin, M., Mitchison, T.J., et al. (2008) Life and Times of a Cellular Bleb. Biophysical Journal, 94, 1836-1853. https://doi.org/10.1529/biophysj.107.113605
- 31. Charras, G.T. (2008) A Short History of Blebbing. Journal of Microscopy-Oxford, 231, 466-478. https://doi.org/10.1111/j.1365-2818.2008.02059.x
- 32. Charras, G.T., Yarrow, J.C., Horton, M.A., et al. (2005) Non-Equilibration of Hydrostatic Pressure in Blebbing Cells. Nature, 435, 365-369. https://doi.org/10.1038/nature03550
- 33. Paluch, E., Piel, M., Prost, J., et al. (2005) Cortical Actomyosin Breakage Triggers Shape Oscillations in Cells and Cell Fragments. Biophysical Journal, 89, 724-733. https://doi.org/10.1529/biophysj.105.060590
- 34. Rintoul, R.C. and Sethi, T. (2001) The Role of Extracellular Matrix in Small-Cell Lung Cancer. The Lancet. Oncology, 2, 437-442. https://doi.org/10.1016/S1470-2045(00)00421-6
- 35. Friedl, P., Borgmann, S. and Brocker, E.B. (2001) Amoeboid Leukocyte Crawling through Extracellular Matrix: Lessons from the Dictyostelium Paradigm of Cell Movement. Journal of Leukocyte Biology, 70, 491-509.
- 36. Friedl, P. and Wolf, K. (2003) Proteolytic and Non-Proteolytic Migration of Tumour Cells and Leucocytes. Biochemical Society Symposium, 277-285. https://doi.org/10.1042/bss0700277
- 37. Yoshida, K. and Soldati, T. (2006) Dissection of Amoeboid Movement into Two Mechanically Distinct Modes. Journal of Cell Science, 119, 3833-3844. https://doi.org/10.1242/jcs.03152
- 38. 樊学军. 细胞力学[J]. 力学进展, 1995, 25(2): 197-208.
- 39. 李敬生, 昌庆, 等. 细胞结构的力学模型及模拟的最新进展[J]. 力学进展, 2004, 34(3): 393-398.
- 40. Lim, C.T., Zhou, E.H. and Quek, S.T. (2006) Mechanical Models for Living Cells—A Review. Journal of Biomechanics, 39, 195-216. https://doi.org/10.1016/j.jbiomech.2004.12.008
- 41. Evans, E. and Yeung, A. (1989) Apparent Viscosity and Cortical Tension of Blood Granulocytes Determined by Micropipet Aspiration. Biophysical Journal, 56, 151-160. https://doi.org/10.1016/S0006-3495(89)82660-8
- 42. 李宝龙. 细胞骨架力学模型的研究进展[J]. 四川建筑科学, 2004, 40(2): 34-38.
- 43. Lauffenburger, D.A. and Horwitz, A.F. (1996) Cell Migration: A Physically Integrated Molecular Process. Cell, 84, 359-369. https://doi.org/10.1016/S0092-8674(00)81280-5
- 44. Ridley, A.J., Schwartz, M.A., Burridge, K., et al. (2003) Cell Migration: Integrating Signals from Front to Back. Science, 302, 1704-1709. https://doi.org/10.1126/science.1092053
- 45. Friedl, P. and Wolf, K. (2009) Proteolytic Interstitial Cell Migration: A Five-Step Process. Cancer and Metastasis Reviews, 28, 129-135. https://doi.org/10.1007/s10555-008-9174-3
- 46. Gibson, L.J. and Ashby, M.F. (1982) The Mechanics of Three-Dimensional Cellular Materials. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 382, 43-59. https://doi.org/10.1098/rspa.1982.0088
- 47. Ingber, D.E. (1993) Cellular Tensegrity: Defining New Rules of Biological Design That Govern the Cytoskeleton. Journal of Cell Science, 104, 613-627.
- 48. Ingber, D.E. (1998) Cellular Basis of Mechanotransduction. The Biological Bulletin, 194, 323-325. https://doi.org/10.2307/1543102
- 49. Yeung, A. and Evans, E. (1989) Cortical Shell-Liquid Core Model for Passive Flow of Liquid-Like Spherical Cells into Micropipets. Biophysical Journal, 56, 139-149. https://doi.org/10.1016/S0006-3495(89)82659-1
- 50. Theret, D.P., Levesque, M.J., Sato, M., et al. (1988) The Application of a Homogeneous Half-Space Model in the Analysis of Endothelial Cell Micropipette Measurements. Journal of Biomechanical Engineering, 110, 190-199. https://doi.org/10.1115/1.3108430
- 51. Schmid-Schonbein, G.W., Sung, K.L., Tozeren, H., et al. (1981) Passive Mechanical Properties of Human Leukocytes. Biophysical Journal, 36, 243-256. https://doi.org/10.1016/S0006-3495(81)84726-1
- 52. Satcher, R.L., Jr. and Dewey, C.F., Jr. (1996) Theoretical Estimates of Mechanical Properties of the Endothelial Cell Cytoskeleton. Biophysical Journal, 71, 109-118. https://doi.org/10.1016/S0006-3495(96)79206-8
- 53. Stamenovic, D. and Coughlin, M.F. (1999) The Role of Prestress and Architecture of the Cytoskeleton and Deformability of Cytoskeletal Filaments in Mechanics of Adherent Cells: A Quantitative Analysis. Journal of Theoretical Biology, 201, 63-74. https://doi.org/10.1006/jtbi.1999.1014
- 54. Stamenovic, D. and Coughlin, M.F. (2000) A Quantitative Model of Cellular Elasticity Based on Tensegrity. Journal of Biomechanical Engineering, 122, 39-43.
- 55. Coughlin, M.F. and Stamenovic, D. (2003) A Prestressed Cable Network Model of the Adherent Cell Cytoskeleton. Biophysical Journal, 84, 1328-1336. https://doi.org/10.1016/S0006-3495(03)74948-0
- 56. Ross, C. and Ethier, C.A.S. (2007) Introductory Biomechanics: From Cells to Organisms.
- 57. Wang, N., Butler, J.P. and Ingber, D.E. (1993) Mechanotransduction across the Cell Surface and through the Cytoskeleton. Science, 260, 1124-1127. https://doi.org/10.1126/science.7684161
- 58. Wang, N. and Ingber, D.E. (1994) Control of Cytoskeletal Mechanics by Extracellular Matrix, Cell Shape, and Mechanical Tension. Biophysical Journal, 66, 2181-2189. https://doi.org/10.1016/S0006-3495(94)81014-8
- 59. Hubmayr, R.D., Shore, S.A., Fredberg, J.J., et al. (1996) Pharmacological Activation Changes Stiffness of Cultured Human Airway Smooth Muscle Cells. The American Journal of Physiology, 271, C1660-C1668.
- 60. Cai, S., Pestic-Dragovich, L., O’donnell, M.E., et al. (1998) Regulation of Cytoskeletal Mechanics and Cell Growth by Myosin Light Chain Phosphorylation. American Journal of Physiology-Cell Physiology, 275, C1349-C1356.
- 61. Mcconnaughey, W.B. and Petersen, N.O. (1980) Cell Poker: An Apparatus for Stress-Strain Measurements on Living Cells. The Review of Scientific Instruments, 51, 575-580. https://doi.org/10.1063/1.1136256
- 62. Petersen, N.O., Mcconnaughey, W.B. and Elson, E.L. (1982) Dependence of Locally Measured Cellular Deformability on Position on the Cell, Temperature, and Cytochalasin B. Proceedings of the National Academy of Sciences of the United States of America, 79, 5327-5331. https://doi.org/10.1073/pnas.79.17.5327
- 63. Zahalak, G.I., Mcconnaughey, W.B. and Elson, E.L. (1990) Determination of Cellular Mechanical Properties by Cell Poking, with an Application to Leukocytes. Journal of Biomechanical Engineering, 112, 283-294. https://doi.org/10.1115/1.2891186
- 64. Bausch, A.R., Ziemann, F., Boulbitch, A.A., et al. (1998) Local Measurements of Viscoelastic Parameters of Adherent Cell Surfaces by Magnetic Bead Microrheometry. Biophysical Journal, 75, 2038-2049. https://doi.org/10.1016/S0006-3495(98)77646-5
- 65. Bausch, A.R., Hellerer, U., Essler, M., et al. (2001) Rapid Stiffening of Integrin Receptor-Actin Linkages in Endothelial Cells Stimulated with Thrombin: A Magnetic Bead Microrheology Study. Biophysical Journal, 80, 2649-2657. https://doi.org/10.1016/s0006-3495(01)76234-0
- 66. Dong, C., Skalak, R. and Sung, K.L. (1991) Cytoplasmic Rheology of Passive Neutrophils. Biorheology, 28, 557-567.
- 67. Hochmuth, R.M., Ting-Beall, H.P., Beaty, B.B., et al. (1993) Viscosity of Passive Human Neutrophils Undergoing Small Deformations. Biophysical Journal, 64, 1596-1601. https://doi.org/10.1016/S0006-3495(93)81530-3
- 68. Tsai, M.A., Frank, R.S. and Waugh, R.E. (1993) Passive Me-chanical Behavior of Human Neutrophils: Power-Law Fluid. Biophysical Journal, 65, 2078-2088. https://doi.org/10.1016/s0006-3495(93)81238-4
- 69. Dong, C., Skalak, R., Sung, K.L., et al. (1988) Passive Deformation Analysis of Human Leukocytes. Journal of Biomechanical Engineering, 110, 27-36. https://doi.org/10.1115/1.3108402
- 70. Mow, V.C., Kuei, S.C., Lai, W.M., et al. (1980) Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression? Theory and Experiments. Journal of Biomechanical Engineering, 102, 73-84. https://doi.org/10.1115/1.3138202
- 71. Leterrier, J.F. (2001) Water and the Cytoskeleton. Cellular and Molecular Biology, 47, 901-923.
- 72. Shin, D. and Athanasiou, K. (1999) Cytoindentation for Obtaining Cell Biomechanical Properties. Journal of Orthopaedic Research, 17, 880-890. https://doi.org/10.1002/jor.1100170613
- 73. Mahaffy, R.E., Shih, C.K., Mackintosh, F.C., et al. (2000) Scanning Probe-Based Frequency-Dependent Microrheology of Polymer Gels and Biological Cells. Physical Review Letters, 85, 880-883. https://doi.org/10.1103/PhysRevLett.85.880
- 74. Maksym, G.N., Fabry, B., Butler, J.P., et al. (2000) Mechanical Properties of Cultured Human Airway Smooth Muscle Cells from 0.05 to 0.4 Hz. Journal of Applied Physiology, 89, 1619-1632.
- 75. Fabry, B., Maksym, G.N., Butler, J.P., et al. (2001) Scaling the Microrheology of Living Cells. Physical Review Letters, 87, 4. https://doi.org/10.1103/PhysRevLett.87.148102
- 76. Alcaraz, J., Buscemi, L., Grabulosa, M., et al. (2003) Microrheology of Human Lung Epithelial Cells Measured by Atomic Force Microscopy. Biophysical Journal, 84, 2071-2079. https://doi.org/10.1016/S0006-3495(03)75014-0
- 77. Mijailovich, S.M., Kojic, M., Zivkovic, M., et al. (2002) A Finite Element Model of Cell Deformation during Magnetic Bead Twisting. Journal of Applied Physiology, 93, 1429-1436. https://doi.org/10.1152/japplphysiol.00255.2002
- 78. 余昶, 张怡, 刘肖珩. 流体剪切应力诱导内皮细胞迁移的力学-化学信号途径[J]. 航天医学工程, 2007, 20(4): 308-312.
- 79. 彭亦良, 梁后杰. 癌细胞运动与迁移的分子机制[J]. 中国生物化学与分子生物学报, 2006, 22(10): 794-798.
- 80. Zigmond, S.H., Levitsky, H.I. and Kreel, B.J. (1981) Cell Polarity: An Examination of Its Behavioral Expression and Its Consequences for Polymorphonuclear Leukocyte Chemotaxis. The Journal of Cell Biology, 89, 585-592. https://doi.org/10.1083/jcb.89.3.585
- 81. Weiner, O.D. (2002) Regulation of Cell Polarity during Eukaryotic Chemotaxis: The Chemotactic Compass. Current Opinion in Cell Biology, 14, 196-202. https://doi.org/10.1016/S0955-0674(02)00310-1
- 82. Hoeller, O. and Kay, R.R. (2007) Chemotaxis in the Absence of PIP3 Gradients. Current Biology, 17, 813-817. https://doi.org/10.1016/j.cub.2007.04.004
- 83. Van Haastert, P.J.M. and Bosgraaf, L. (2009) The Local Cell Curvature Guides Pseudopodia towards Chemoattractants. Hfsp Journal, 3, 282-286. https://doi.org/10.2976/1.3185725
- 84. King, J.S. and Insall, R.H. (2009) Chemotaxis: Finding the Way forward with Dictyostelium. Trends in Cell Biology, 19, 523-530. https://doi.org/10.1016/j.tcb.2009.07.004
- 85. Bahat, A., Caplan, S.R. and Eisenbach, M. (2012) Thermotaxis of Human Sperm Cells in Extraordinarily Shallow Temperature Gradients over a Wide Range. PLoS ONE, 7, e41915. https://doi.org/10.1371/journal.pone.0041915
- 86. Zhao, M. (2009) Electrical Fields in Wound Healing—An Overriding Signal That Directs Cell Migration. Seminars in Cell & Developmental Biology, 20, 674-682. https://doi.org/10.1016/j.semcdb.2008.12.009
- 87. Zaman, M.H., Kamm, R.D., Matsudaira, P., et al. (2005) Computational Model for Cell Migration in Three-Dimen- sional Matrices. Biophysical Journal, 89, 1389-1397. https://doi.org/10.1529/biophysj.105.060723
- 88. Dokukina, I.V. and Gracheva, M.E. (2010) A Model of Fibroblast Motility on Substrates with Different Rigidities. Biophysical Journal, 98, 2794-2803. https://doi.org/10.1016/j.bpj.2010.03.026
- 89. Lo, C.M., Wang, H.B., Dembo, M., et al. (2000) Cell Movement Is Guided by the Rigidity of the Substrate. Biophysical Journal, 79, 144-152. https://doi.org/10.1016/S0006-3495(00)76279-5
- 90. Discher, D.E., Janmey, P. and Wang, Y.L. (2005) Tissue Cells Feel and Respond to the Stiffness of Their Substrate. Science, 310, 1139-1143. https://doi.org/10.1126/science.1116995
- 91. Wong, H.C. and Tang, W.C. (2011) Computational Study of Local and Global ECM Degradation and the Effects on Cell Speed and Cell-Matrix Tractions. Nano Communication Networks, 2, 119-124. https://doi.org/10.1016/j.nancom.2011.05.005
- 92. Jamaleddin Mousavi, S., Hamdy Doweidar, M. and Doblare, M. (2013) 3D Computational Modelling of Cell Migration: A Mechano-Chemo-Thermo-Electrotaxis Approach. Journal of Theoretical Biology, 329, 64-73. https://doi.org/10.1016/j.jtbi.2013.03.021
- 93. Mousavi, S.J., Doweidar, M.H. and Doblare, M. (2014) Computational Modelling and Analysis of Mechanical Conditions on Cell Locomotion and Cell-Cell Interaction. Computer Methods in Biomechanics and Biomedical Engineering, 17, 678-693. https://doi.org/10.1080/10255842.2012.710841
- 94. Bosgraaf, L. and Van Haastert, P.J.M. (2009) Navigation of Chemotactic Cells by Parallel Signaling to Pseudopod Persistence and Orientation. PLoS ONE, 4, e6842. https://doi.org/10.1371/journal.pone.0006842
- 95. Higazi, A.A., Kniss, D., Manuppello, J., et al. (1996) Thermotaxis of Human Trophoblastic Cells. Placenta, 17, 683- 687. https://doi.org/10.1016/S0143-4004(96)80019-1
- 96. Nishimura, K.Y., Isseroff, R.R. and Nuccitelli, R. (1996) Human Keratinocytes Migrate to the Negative Pole in Direct Current Electric Fields Comparable to Those Measured in Mammalian Wounds. Journal of Cell Science, 109, 199-207.
- 97. Gou, X., Yang, H., Fahmy, T.M., et al. (2014) Direct Measurement of Cell Protrusion Force Utilizing a Robot-Aided Cell Manipulation System with Optical Tweezers for Cell Migration Control. The International Journal of Robotics Research, 33, 1782-1792. https://doi.org/10.1177/0278364914546536
- 98. Yang, H., Gou, X., Wang, Y., et al. (2015) A Dynamic Model of Chemoattractant-Induced Cell Migration. Biophysical Journal, 108, 1645-1651. https://doi.org/10.1016/j.bpj.2014.12.060
- 99. Van Haastert, P.J.M. (2010) Chemotaxis: Insights from the Extending Pseudopod. Journal of Cell Science, 123, 3031- 3037. https://doi.org/10.1242/jcs.071118
- 100. Allena, R. (2013) Cell Migration with Multiple Pseudopodia: Temporal and Spatial Sensing Models. Bulletin of Mathematical Biology, 75, 288-316. https://doi.org/10.1007/s11538-012-9806-1
- 101. Allena, R. and Aubry, D. (2012) “Run-and-Tumble” or “Look-and-Run”? A Mechanical Model to Explore the Behavior of a Migrating Amoeboid Cell. Journal of Theoretical Biology, 306, 15-31. https://doi.org/10.1016/j.jtbi.2012.03.041