International Journal of Mechanics Research
Vol.06 No.04(2017), Article ID:23044,12
pages
10.12677/IJM.2017.64019
Simulation of Material Constitution and Buckling Analysis Based on a Truss Model
Wei Liu, Zheng Zhang
Institute of Solid Mechanics, Beijing University of Aeronautics and Astronautics, Beijing

Received: Nov. 28th, 2017; accepted: Dec. 11th, 2017; published: Dec. 18th, 2017

ABSTRACT
The mechanical behavior of the truss model is simulated, and the corresponding frame model is constructed for the orthogonal anisotropy and the isotropic material in this paper. The model parameters are determined according to the constitutive relation of the material (Hooke’s law). The influence of the Poisson’s ratio on the model structure validates the applicability of the model and the rationality of the truss model to simulate the mechanical behavior is also discussed. This paper uses the truss model to study the behavior of the material flexing for the isotropic material, the basic parameters of the truss model and the buckling behavior of the material bar are combined to establish the criterion of the flexion failure of the frame model. Failure of the material mesoscopic mechanism is finally discussed.
Keywords:Constitutive Relation, Truss Model, Poisson’s Ratio, Buckling, Mesomechanism
材料本构模拟的桁架模型和屈曲问题分析
刘伟,张铮
北京航空航天大学,固体力学研究所,北京
收稿日期:2017年11月28日;录用日期:2017年12月11日;发布日期:2017年12月18日

摘 要
本文建立桁架模型模拟材料的力学行为,针对正交各向异性和各向同性材料,构建相应的框架模型,并依据材料的本构关系(胡克定律)确定模型参数。本文进一步讨论了材料泊松比对模型构造的影响,验证了模型的适用性和桁架模型模拟力学行为的合理性。对于各向同性材料,本文应用该桁架模型对材料曲屈行为进行了研究,将桁架模型的基本参数确定与材料杆件屈曲行为结合起来,建立框架模型曲屈失效的判据,探讨了杆件失效的材料细观机制。
关键词 :本构关系,桁架模型,泊松比,屈曲,细观机制

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 前言
桁架结构由若干杆件和连接杆件的铰点组成,杆件通过铰点相互作用;桁架结构形式简单、拆卸方便,运输便利,是一种应用十分广泛的工程结构形式。桁架结构中各个杆件受力情况不尽相同,通过合理设计桁架结构,可使各杆最大限度地发挥自身的力学性能,从而有效减轻结构整体重量,是桁架结构应用的关键。
在框架模型的发展中,Schmit构建了多工况情形中弹性结构优化的数学模型 [1] ,采用应用数学规划法来优化设计;Cornell构造以运动极限为准则的线性序列法 [2] ,桁架杆件截面积得到了优化;Bendsoe将桁架结构以重量为约束条件,以位移为设计变量,按照最小势能原理求解原问题极值 [3] ;刘亮等人以有限元法为基础,建立了杆单元位移的计算方法,将结构设计的优化变量与模型参数之间的关系用显式表达 [4] ;程耿东和郭旭提出变量 释放的算法 [5] ,得到了桁架结构的奇异问题的最优解,从而通过已有的拓扑优化算法得到全局最优解。
上述工作主要是针对结构分析,与此不同的是,本文以桁架结构为基础,将桁架这种非连续介质形式用于一般连续介质的力学行为模拟上,通过桁架受力平衡分析,建立桁架中杆件受力平衡关系与被模拟材料的本构关系的当量性,从而建立起桁架模型参数与被模拟材料参数的关系,达到桁架模型变形与被模拟材料变形的一致性,进而可应用桁架模型研究被模拟材料的力学行为,揭示被模拟材料的力学特性。在其他的本构关系的问题方法中,本文与其推论的理论基础基本相似,而本文建立了更具有一般性的桁架模型。
本文后半部分通过桁架模型对材料曲屈行为进行了研究,桁架模型不仅能够模拟真实材料的力学行为,通过模型构造也可以适用于各种不同性质的材料性能模拟,为材料力学行为研究提供一种新的思路。
2. 桁架模型
2.1. 桁架模型的构成
《断裂与损伤力学》(第二版) [6] 采用如图1(b)所示桁架模型,模拟边长为2l的介质正方体元(参看图1(a)),设桁架模型边长也为2l,桁架包括棱边杆和面心对角杆两类杆件,其本构关系可表示为:
(2.1)
式中, 与 、 与 、 与 均分别为棱边杆与面心杆的轴力、刚度以及伸长量,i、j为杆
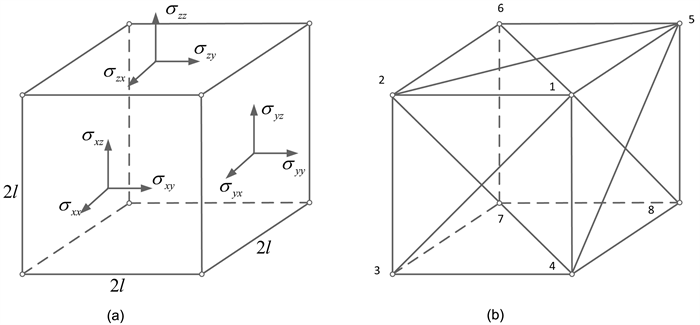
Figure 1. The diagram of truss model. (a) Continuum unit; (b) Truss model
图1. 桁架模型示意图。(a) 连续介质单元;(b) 桁架模型
两端点编号,如图1(b)所示。
2.2. 桁架模型与介质单元的变形一致性
2.2.1. 桁架节点和介质单元的位移关系
首先建立桁架模型与介质(正方形)体元的变形一致性,即桁架模型各个节点的位移与介质体元的位移相等。对于介质体元而言,位移分量 与应变分量 有如下关系(不考虑刚体位移):
(2.2a)
由于介质体元内应变是均匀的,则积分上式有:
(2.2b)
根据桁架模型与介质体元变形一致的设定,可得桁架节点位移分量与体元相应应变分量的关系如下:
(2.3)
式中下标i分别指x,y,z轴,上标为顶点编号。
2.2.2. 桁架的虚功原理
根据虚功原理 [6] ,有
(2.4)
其中,桁架外力虚功 为
(2.5)
即桁架的外虚功可用介质单元的虚应变能表示。桁架内力虚功 为
(2.6)
其中, , 分别是棱边杆与面内杆的内力虚功,即
(2.7)
2.2.3. 桁架的平衡方程(介质应力与桁架内力关系)
将式(2.5)和式(2.6)代入式(2.4),并考虑到式(2.7),由应变变分即虚应变 的独立性,即与介质体元应变相对应的桁架模型变形项的系数,和该介质体元应变项的系数相同,可得:
(2.8)
上式即为由虚功原理得到的桁架节点平衡方程,即在变形一致的前提下,桁架模型与介质体元力学行为等价性条件。将式(2.1)代入上式,即可建立模型参数与材料参数的关系,从而实现用桁架模型模拟材料的力学行为。
2.2.4. 桁架模型参数确定的一般方法
参看图1(b),桁架模型共有12个棱边杆和6个面的12个面内杆。考虑到一般各向异性材料的本构关系 [7] (如下式所示),
(2.9)
令每个棱边杆和面内杆的刚度均不相同,该桁架模型共24个独立参数,而一般各向异性材料的本构参数数目为21个。
将式(2.1)代入式(2.8),化简可得:
(2.10)
其中
桁架模型共24个独立参数,而一般各向异性材料的本构参数数目为21个:桁架模型的24个独立参数分别为12个独立的棱边杆参数和12个独立的面内杆参数,而一般各项异性的参数则是由材料本身的性质所决定了。
3. 正交各向异性材料模拟–桁架模型参数确定
基于上一节的模型,由正交各向异性材料的性质,可设定对应平行棱边杆的材料模量相等,平行面的对应面内杆的材料模量相等。故令三个棱边杆的模量分别为Kxx、Kyy和Kzz,六个面的面内杆的材料模量分别为K13、K24、K16、K25、K18和K45,其中下标为杆两端点编号,编号参看图1(b)。
对于正交各向异性材料,本构关系 [7] 为
(3.1)
其中
(3.2)
通过式(2.10)与式(3.1)比较可知
故令
则式(2.9)简化为
(3.3)
对比式(3.1)和式(3.3)有
(3.4)
由上式可知桁架参数由材料参数计算得到。桁架模型有9个未知杆模量,材料刚度矩阵亦有9个独立常数,桁架模型参数可由材料基本参数唯一确定。
4. 各向同性材料模拟―改进的桁架模型
对各向同性材料而言,式(3.4)中
参考式(3.4)有
(4.1)
即泊松比μ固定为0.25,这一结果大大降低了桁架模型的普适性。
考虑到上述问题,在原有模型中引入六个面的面内剪切板,即只承受剪切、不承受面内拉压的板,为桁架模型加入新的独立参数,以适应材料不同的泊松比。
参考图1,以由节点1234组成的剪切板为例,其剪应变为 ,令其剪切模量为 ,故桁架模型的剪切板的应变能为 ,引入虚功原理得到平衡方程如下:
(4.2)
其中, 为体积应变
线弹性各向同性材料本构关系的一般式为
故有
(4.3)
与各向同性材料的本构关系对比,由式(4.3)可得
(4.4)
从上述结果可以看出,引入剪切板后,材料的泊松比不再固定,可以随着被模拟材料本身的性质变化。值得注意的是,当材料的泊松比大于0.25且小于0.5时,剪切板的弹性模量为负数。而这个结果的产生是因为框架结构既要与介质单元的受力状况相一致,各个节点又要与介质单元对应点的位移相同在此约束下产生的数学结果表现为如上所示。尽管现实中应力应变方向相反的剪切板是不可能存在的,只是以此模拟介质单元的力学性能。
5. 屈曲问题中框架模型的受力形式
5.1. 杆的应力与微元体应力关系
基于宏观杆件屈曲分析,对单个框架的受力进行分析,考察框架的受力形式,建立相应的框架模型失效和实际杆件失效的等效关系,通过对比分析得到的框架模型的失效判据,即各个构件的失效临界载荷。
首先,假设框架模型中某一个或数个构件的应力达到其失效的条件,即认为整个构件失效。其次,设棱边杆和面内杆为同种材料,在此情况下有
(5.1)
此时 ,故令 , 。
根据前文桁架各元件应力与微元体应力关系(2.8)有:
(5.2)
其中 代表以i,j两点为节点的杆的压(拉)力。
对于各项同性材料,根据胡克定律,微元体应力与构件力之间的关系(5.2)可以简化为
(5.3)
其中 , , 分别代表沿x,y,z轴棱边杆的应力, 为被模拟材料的泊松比, 代表以i,j两点为节点的杆截面的压(拉)应力。
5.2. 宏观单向压应力情况下框架模型受力形式
在此引入杆屈曲的宏观受力状态,即载荷方向正压应力 , ,则各个杆的应力状态可简化(5.3)为:
(5.4)
从上述表达式中我们可以总结如下几点:
1) 当某点处于单向应力状态时,各杆的受力状态与被模拟材料的参数有关,也与构件的具体尺寸有关。公式中的 项中 代表了框架模型边长的1/2,故各个杆件的应力数值受杆件的尺寸比例取值影响。
2) 由于被模拟材料的宏观失效形式是杆件屈曲,故在微观上我们亦考察与宏观失效形式相一致的框架模型杆件受压失效形式,而不考虑杆件受拉应力的失效形式。根据式(5.1),棱边杆的弹性模量为
(5.5)
故知:
a) 在 时,棱边杆的弹性模量为正数,与宏观杆屈曲的受力失效形式一致;
b) 在 时,棱边杆的弹性模量为负数,与客观材料情况不一致,不做失效考虑。
3) 应该明确的是,由于构件的材料参数相同,故判别构件失效的依据为压应力较大的构件首先失效,进而建立框架模型的失效判据。故
a) 当 时,最大的受力杆是与受力方向平行的棱边杆,应力为 ,即被模拟材料发生屈曲时,首先发生失效的是的棱边杆;
b) 当 时,与受力方向相平行的面中的面内杆压应力最大,应力为
即被模拟材料发生屈曲时,首先发生失效的是与受力方向相平行的面中的面内杆。
5.3. 宏观三向压应力情况下框架模型受力形式
根据微元体应力与构件力之间的关系(5.3)和(5.4),若微元体受到三向压应力,即
各个杆的应力大小相同,应力数值可简化为:
(5.6)
可以看出当框架模型对应的微元体介质单元处于三向压应力状态时,尽管各杆的受力状态与被模拟材料的参数有关,但棱边杆与面内杆的应力比值是固定的,即 ,所以面内杆的压应力一直大于棱边杆。故在三向压力状态下,若介质单元发生失效,对应框架模型中首先失效的是面内杆。
5.4. 宏观杆件屈曲时截面受力形式
根据弹性力学理论,杆件受到单向载荷作用,在其垂直于载荷的横截面上,边缘部分受力形式接近单项应力状态,中心部分接近三向应力受力状态。若要分析该截面上各个微元体的失效,应对不同受力状况进行具体分析,即比较上述5.2和5.3两小节中处于这两种受力状况下各框架模型的失效形式,比较结果如下:
处于单向应力状态时
1) 若 ,首先发生失效的是的棱边杆,根据式(5.4),其应力为 ;
2) 若 ,首先发生失效的是与受力方向相平行的面中的面内杆,根据式(5.4),应力为
。
处于三向应力状态时
所以对弹性模量和尺寸(截面形状和杆长度)不变的框架杆件,即 不变的杆件,在其失效截面上,有如下推论:
1) 时,在宏观材料杆件横截面中心部分所对应的框架模型中,与受力方向相平行的面中的面内杆应力最大首先失效,即宏观材料杆件横截面中心部分先于边缘部分失效。
2) 时,在宏观材料杆件横截面边缘部分所对应的框架模型中,与受力方向相平行棱边杆应力最大首先失效,即宏观材料杆件横截面边缘部分先于中心部分失效。
3) 时,在宏观材料杆件横截面边缘部分所对应的框架模型中,与受力方向相平行的面中的面内杆应力最大首先失效,即宏观材料杆件横截面边缘部分先于中心部分失效。
5.5. 本章小结
综上所述,以宏观杆理论分析的屈曲载荷为参照,通过对应的框架模型研究,建立了框架模型的相应的失效判据,即在宏观杆屈曲的应力状态下,首先失效的是相应框架模型压应力大的杆,亦即框架模型失效。
从上述模型失效研究中我们看到,对于宏观杆材料的不同泊松比,框架模型的失效形式是不同的,由此可以反映出该宏观杆材料屈曲特性的不同。我们认为框架模型棱边杆失效时,宏观杆屈曲是由压应力主导的;框架模型与受力方向相平行的面中的面内杆失效时,宏观杆屈曲是由相应的剪切应力主导的。上述分析和认识基于本文的模型研究,与宏观杆屈曲的理论分析相一致,尚缺乏相应的细观材料实验研究。因此,上述结论属于假说性质,但对宏观杆及材料的屈曲机制和行为具有一定的揭示和借鉴意义。
6. 本文小结
本文提出的桁架模型中,杆件只承受杆的轴向力,面内板只受剪切力作用,不承受面内拉压作用;该桁架模型有八个节点,十二个棱边杆、十二个面内杆和六个剪切板,对于不同类型和性质的材料,可具体设定模型杆件和剪切板的材料模量;本文基于桁架模型和被模拟介质体元变形一致的前提,通过虚功原理建立桁架模型与被模拟介质体元的刚度等效关系,从而用材料参数确定桁架模拟模型的参数。
1) 对于各向同性材料,本文在原模型的基础上添加了只承受剪切的面板元件,解决了桁架模型对材料泊松效应的模拟问题。
2) 由改进的桁架模拟模型可知,引入的剪切板材料剪切板模量 时,被模拟的材料泊松比为0.25;值得注意到的是,当材料的泊松比大于0.25且小于0.5时,桁架模型剪切板的材料剪切模量为负,即该剪切板的应力应变方向相反。
3) 基于框架模型的建立继而分析屈曲变化的引发机制,并结合框架模型计算对屈曲问题进行分析,讨论细长构件在压缩载荷下从压缩变形到弯曲变形的变化过程和力学作用,特别是在临界屈曲载荷下,分析框架模型的受力状况。
4) 从模型失效研究中我们看到,对于宏观杆材料的不同泊松比,框架模型的失效形式是不同的,由此可以反映出该宏观杆材料屈曲特性的不同。我们认为框架模型棱边杆失效时,宏观杆屈曲是由压应力主导的;框架模型与受力方向相平行的面中的面内杆失效时,宏观杆屈曲是由相应的剪切应力主导的。
上述结果表明,桁架模型不仅能够模拟真实材料的力学行为,通过模型构造也可以适用于各种不同性质的材料性能模拟,为材料力学行为研究提供了一种新的方式。
文章引用
刘 伟,张 铮. 材料本构模拟的桁架模型和屈曲问题分析
Simulation of Material Constitution and Buckling Analysis Based on a Truss Model[J]. 力学研究, 2017, 06(04): 180-191. http://dx.doi.org/10.12677/IJM.2017.64019
参考文献 (References)
- 1. Schmit, L.A. (1960) Structural Design by Systematic Synthesis. 2nd Conference on Electronic Computation, ASCE, New York, 105-122.
- 2. Cornell, C.A. (1968) Examples of Optimization Design: An Introduction to Structural Optimization. Solid Mechanics Division, University of Waterloo, Waterloo.
- 3. Bendsoe, M.P., Bed-Tal, A. and Zowe, J. (1994) Optimization Methods for Truss Geometry and Topology Design. Structural Optimization, 17, 981-1002. https://doi.org/10.1007/BF01742459
- 4. 刘亮, 翟宇毅. 桁架结构重分析的一种新方法[J]. 计算力学学报, 1998, 5(2): 149-152.
- 5. Cheng, G.D. and Xu, G. (1997) ε-Relaxed Approach Structural Topology Optimization. Structural Optimization, 13, 152-166. https://doi.org/10.1007/BF01197454
- 6. 张行. 断裂与损伤力学[M]. 第二版. 北京: 北京航空航天大学出版社, 2009.
- 7. 王耀先. 复合材料力学与结构设计[M]. 上海: 华东理工大学出版社, 2012.