International Journal of Mechanics Research
Vol.07 No.02(2018), Article ID:25507,12
pages
10.12677/IJM.2018.72007
Some Advances in Fracture Mechanics of Thermoelectric Material
Qingnan Liu, Shenghu Ding*
School of Mathematical Statistics, Ningxia University, Yinchuan Ningxia

Received: Jun. 1st, 2018; accepted: Jun. 14th, 2018; published: Jun. 21st, 2018

ABSTRACT
Thermoelectric material is a kind of functional material which converts heat energy and electric energy to each other. Since the constitutive equations of thermoelectric materials are nonlinear and the corresponding mechanical analysis is very challenging, it is of great significance to sort out the research progress of thermoelectric materials in fracture mechanics. In this paper, the development status and application prospect of thermoelectric materials are introduced. The latest research progress of fracture mechanics of thermoelectric materials is reviewed, including the theoretical research and numerical study of thermoelectric materials fracture mechanics, and experimental research in fracture mechanics of thermoelectric materials. Finally, the future research on the fracture mechanics of thermoelectric materials is prospected.
Keywords:Thermoelectric Materials, Crack, Fracture Mechanics, Numeral Calculation
热电材料断裂力学的若干进展
刘庆楠,丁生虎*
宁夏大学,数学统计学院,宁夏 银川

收稿日期:2018年6月1日;录用日期:2018年6月14日;发布日期:2018年6月21日

摘 要
热电材料是一种将热能和电能进行转换的功能材料。由于热电材料的本构方程是非线性的,相应的力学分析具有很大的挑战性,因此对热电材料在断裂力学中的研究进展进行梳理具有十分重要的意义。本文介绍了热电材料的发展现状和应用前景,综述了热电材料断裂力学的最新研究进展,包括热电材料断裂力学问题的理论研究、数值研究和热电材料断裂力学中的实验研究。最后对未来热电材料的断裂力学研究进行了展望。
关键词 :热电材料,裂纹,断裂力学,数值计算

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
热电材料作为一种被广泛应用的环境友好型材料,已成为国际材料研究领域的热点课题之一。它是一种利用固体内部载流子的运动实现热能和电能直接相互转换的功能材料,在能源、制冷、微电子、航天、军事等领域有着广泛的应用 [1] 。它因体积小、重量轻、无传动部件、无噪声运行、精确可靠等优点引起了越来越多学者的重视。由于材料的脆断总是由宏观裂纹引起的 [2] ,如夹杂,加工,热载荷,电载荷等都会引起裂纹,热电材料是脆性的并且容易因热冲击损坏,因此必须对热电材料的断裂性能进行分析研究。本文主要介绍了运用断裂力学理论来研究热电材料中裂纹尖端附近的应力、应变场和裂纹的扩展规律。
2.热电材料
2.1. 热电材料的发展与背景
热电材料是一种有着广泛应用前景的材料。在环境污染和能源危机日益严重的今天,进行新型热电材料的研究具有很强的现实意义。热电技术将余热转化为电能可以作为解决能源问题的可行方案 [3] ,材料的选择可依其运作温度分为三类 [4] :第一类为碲化铋及其合金,用于热电致冷器;第二类为碲化铅及其合金,用于热电产生器;第三类为硅锗合金,常应用于热电产生器。热电效应在发电和致冷方面有着巨大的应用价值 [5] 。1821年发现的塞贝克效应和1834年发现的帕尔帖效应为热电能量转换器和热电制冷的应用提供了理论依据 [6] 。Seebeck通过加热两个不同电导体之间的连接处来产生电动势发现第一个热电效应。Peltier观察到了当电流从不同材料之间传递时会对材料连接处加热或冷却发现第二个热电效应。塞贝克和珀尔帖现象是相互依存的,这种相互依赖性称为汤姆逊效应,即当有电流和温度梯度时加热或冷却都是可逆的 [7] 。
2.2. 影响热电材料能量转换的因素
热电材料可以将废热转换成电力,从而提高燃料效率,被认为是最有前途的技术材料。热电材料的能量转换效率用优值Z来衡量 [8] ,Z值越大热电材料的热电转换能力也越强。也常用无量纲因子ZT来表示这一特性,ZT值是由塞贝克系数,电导率以及热导率这几个参数来表征
(1)
其中 是热电材料的塞贝克系数, 是热电材料的电导率, 是热电材料的热导率。
Hicks等人提出热电材料的低维化有利于提高热电材料的热电优值,而电子和孔洞的存在会降低热电材料的优值 [9] 。优值Z受材料的种类、组分、掺杂比例和具体结构影响。优值与材料的塞贝克系数以及电导率、热导率有关,同时这三个参数都与温度相关。热电材料是一种非均匀功能梯度材料,现阶段提升热电材料转换能力的措施有以下几种 [10] :首先,最直接的措施是提高热电材料的塞贝克系数。通过改变热电材料内部的构造以及化学合成成分来提高热电材料的塞贝克系数,具体方法有参杂、杂质替代等。通过理论分析及大量实验来寻找塞贝克系数较大的热电材料。其次,可以通过提高载流子的密度、提高载流子迁移率等方式来提高电导率 [11] ,但这些方法同时会使塞贝克系数降低,整体效果不太明显。最后,降低材料的热导率成为提高材料热电性能的主要方法。Bi2Te3基热电材料是最常见具有低的热导率和较高的热导率的热电材料,因而广泛应用于热电制冷和利用温差发电技术等领域。常见的热电材料还有硫属化铅基热电材料,用高能球磨法制备的BiSbTe纳米晶块体材料和p型MgAgSb基热电材料,三种热电材料的晶体结构图见图1 [12] 。因其晶体结构的不同而被应用于热电能量转换器和热电制冷等不同领域。例如市面上的一种移动型冰箱,具有无噪音体积小便于携带等优点,天气冷时还可变为保温器,这种冰箱应用的就是热电材料。还有利用温差产生电力来驱动手表等技术都是热电材料的发展及应用。
Zhang和Wang用解析法研究了对矩形热电板施加电和温度载荷,计算了裂纹尖端的电流密度和能量通量强度因子,结果显示可以通过增加裂纹尺寸来降低热导率 [13] 。化学家们将钠原子添加到一种具有有序晶格结构的热电材料中以增加材料的导电性,允许电子穿过材料的裂缝以减缓热量的传播 [14] 。在用保角映射函数和Mori-Tanaka方法研究椭圆体热电复合材料的性能时,发现通过增加填充率可以降低电导率和热导率 [15] 。其次高温高压也可以降低材料的电阻率得到极低的热导率,通过电学测试发现高压对材料的热电性能影响不大 [16] 。
3. 热电材料断裂力学的理论分析
断裂力学是研究材料裂纹扩展规律的学科,从裂纹起裂、扩展到失稳过程都在其分析范围内。其核心任务就是求解含各种缺陷的固体材料或结构在外载荷作用下的应力、应变场和确定裂纹尖端处的应力强度因子,应力强度因子是衡量裂纹尖端区应力场强度的参量 [17] 。
裂纹尖端应力场强度表示为
(2)
其中
为应力分量,K为应力强度因子,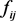 为极坐标角
的函数。
为极坐标角
的函数。
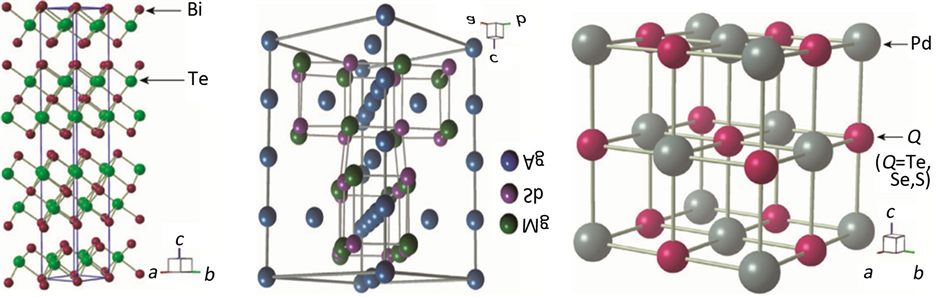
Figure 1. Crystal structure diagram of three different thermoelectric materials
图1. 三种不同的热电材料的晶体结构图
在断裂力学研究中,断裂准则是含裂纹构件的应力强度因子小于材料断裂韧度时,裂纹不扩展,构件安全;反之,裂纹扩展,构件不安全 [18] 。由于热电材料通常是脆性半导体材料,因其固有的脆性和低的韧性,对热电材料施加力、热或电载荷时,材料会出现裂纹或微裂纹的情况,所以要对裂纹尖端场进行分析。
热电材料断裂理论研究的求解方法中,最常见的是Westergaard应力函数法和Muskhelishvili方法。对于张开型和滑开型裂纹在求解时通常使用Westergaard应力函数法,而在研究复合型裂纹时习惯使用Muskhelishvili应力函数法。Muskhelishvili方法是通过保角变换将物理平面上的区域映射为数学平面上的单位圆上去求解。由于复变函数的实部和虚部都满足Laplace方程,求解共轭的调和函数。如果知道一个调和函数,则可以由柯西–黎曼方程求出与之共轭的调和函数。对于Muskhelishvili方法在求解二维平面问题时需要求解两个解析函数,而Westergaard应力函数法在求解过程中,可以不必先求得应力场,而先求得复应力函数从而求解应力强度因子,只需要求解一个解析函数。从断裂力学的观点来看,对于大多数结构和零件来说,宏观裂纹的存在是不可避免的。用复变函数方法研究热电材料裂纹的二维问题,求解热电材料断裂力学中的裂纹问题,首要解决的是裂纹尖端应力奇异性 [19] 。
设静止条件下,仅在平面内考察无限均匀热电材料,假设自由电荷和热源不存在,热电材料控制场方程为
(3)
(4)
其中V是电势,T是温度, 是电流密度,q是热通量, 、 和 分别是电导率热导率和赛贝克系数。
由于能量能通过电子和热传输,因此能量通量表示为
(5)
Zhang和Wang用复变函数方法解决了无限介质中的裂纹问题 [20] ,得出了热通量,电通量和裂纹尖端附近的应力场表达式
(6)
(7)
(8)
边界条件为
(9)
其中常数项 和 是施加到边界上的外力。结果表明:电通量强度因子和热流强度因子取决于远场电
通量负荷和应用的总能量的负荷。同样地运用复变函数方法和共形映射方法,还研究了椭圆孔或裂纹的二维问题 [21] 。研究发现当椭圆孔退化为贯通裂纹时,裂纹尖端处的电流密度,能量通量,热通量和应力场呈现传统的平方根奇异性。之后Zhang等人基于电和热的非线性耦合控制方程,采用傅里叶变换和奇异积分方程分析了裂纹为有限高和宽的热电材料的热电转换效率,得出在有裂纹的热电材料中可以得到更高的转换效率 [22] 。Zeleke在不考虑材料中缺陷的影响下,使用经典理论同时对热电转换器中的热和电流进行建模。利用广义傅立叶定律和欧姆定律的动力学方程,导出了耦合热电现象的能量守恒和电荷守恒的动力学方程 [23] 。Wang首次建立了热电材料的倾斜椭圆形热电耦合的理论模型。讨论了双轴加载下椭圆孔的扩展问题。结果表明:对于双轴加载椭圆孔,由于非线性耦合,解不能是两个单轴受力情况的解的线性叠加。当长轴垂直于加载方向时有最大的热电集中 [24] 。
热电材料在服役期间常因热冲击而产生机械失效甚至断裂 [25] ,因此对热电材料的热冲击应力及断裂分析是非常必要的。Jin对多层热电薄膜材料的热应力进行了研究。通过建立新的模型得到比材料强度模型更高的热应力 [26] ,同时研究了Bi2Te3基于沿其厚度方向的一维温度荷载作用下的热电材料板,解决了稳态和瞬态时的温度场和应力场 [27] 。基于奇异积分方程研究热电薄膜,发现在薄膜末端剪切应力存在奇异性。讨论了界面导电率的影响以及薄膜的弹塑性变形 [28] 。郭亚博用解析法研究了单层热电材料板和层合热电材料板的热冲击,发现应力强度因子随着热电材料板厚度的增加而增加,而热冲击阻力随着热电材料板的厚度的增加而减小,也得到了在稳态和瞬态状态下的相关温度和应力场 [29] 。在此基础上Wang等人研究了沿其厚度方向施加热载荷的Bi2Te3热电材料板,同样得到了稳态和瞬态中的相关温度和应力场表达式,发现瞬态应力远大于稳态应力,应力强度因子随着板厚度的增加而增加。如图2表示了三种不同厚度热电材料板的热冲击阻力,可知当板较薄时,抗热冲击性的值增大 [30] 。
Huang对热电薄膜制冷器的热应力进行了研究,假定汤姆逊效应的冷却功率,对一维和二维温度场和应力场进行了分析,发现了热应力的分层结构和温度差引起的非耦合热弹性理论可以作为判定薄膜结构是否受热应力破坏,并对相邻层间的剪切应力提供了初步认识 [31] 。Hikage等人研究了热电发电器的热膨胀,得到了热电材料的热膨胀系数受材料内部晶体大小的影响的结论 [32] 。在此之后Ravi等人对高温热电材料的热膨胀性能进行了研究,证明了热电材料的热膨胀系数对材料的内部应力大小具有重要影响 [33] 。Chuan-Bin研究了无限远热电介质中圆弧裂纹的平面问题。结果表明,电通量强度因子和能量通量强度因子分别取决于远场电通量负荷和施加的总能量通量负荷 [34] 。Song等在研究热电材料裂纹问题中用复变函数方法,讨论裂纹对热电材料的转换效率的影响,分析了当电流流动和热通量分离时,热电转换效率可以高于在相同温度条件下一维热电偶的最大转换效率 [35] 。文中给出电流密度和热通量的表达式为
(10)
(11)
由(10)和(11)式可知,在热和电不可渗透裂纹的情况下,电流密度和热通量在裂纹尖端处具有奇异性。
(12)
(13)
由(12)和(13)式可知,在电渗透热不渗透裂纹的时候,电流密度在裂纹尖端处没有奇异性,热通量具有平方根奇异性。
Wang采用有限厚度切口方法讨论了裂纹表面热电边界条件对材料的影响 [36] 。之后用复变函数法研究了填充在裂纹中的空气的导热率以及裂纹厚度对裂纹尖端场的影响 [37] 。如图3和图4为热电材料中裂纹为a时裂纹表面的温度场和电势场,发现裂纹内的空气的导热性不能忽略,并且应该考虑裂纹的有限厚度的影响。
Ding等人研究了梯度非均匀材料的热弹性断裂,探究材料非均匀性参数和热阻对热应力强度因子的影响,热阻的变化会显著影响到裂纹表面的温度 [38] 。为更好的研究梯度层的热行为提供了依据。之后Ding和Li使用傅立叶变换、叠加原理和奇异积分方程等方法研究受热与机械应力载荷下部分绝缘的两种不同功能梯度材料间的界面裂纹,推导出温度和位移场的表达式。同时对材料的非均匀性参数,热应力强度因子和最小应变能密度进行了研究 [39] 。
4. 热电材料断裂的数值研究
对于较为复杂的热电材料裂纹问题的研究,数值计算方法是非常有效的分析工具。例如有限差分法、有限元法、边界元法、非连续变形分析等。基于有限元方法,Pérez-Aparicio等人研究了热电偶的二维珀尔
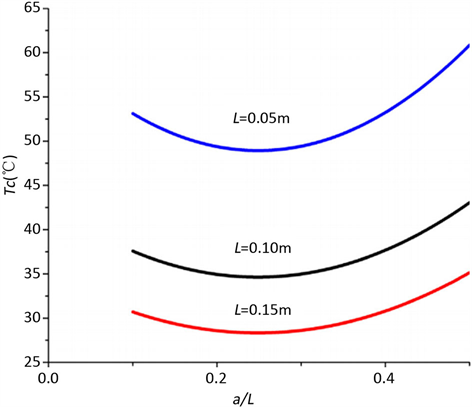
Figure 2. Thermal shock function of different thickness plates
图2. 不同厚度板的热冲击函数
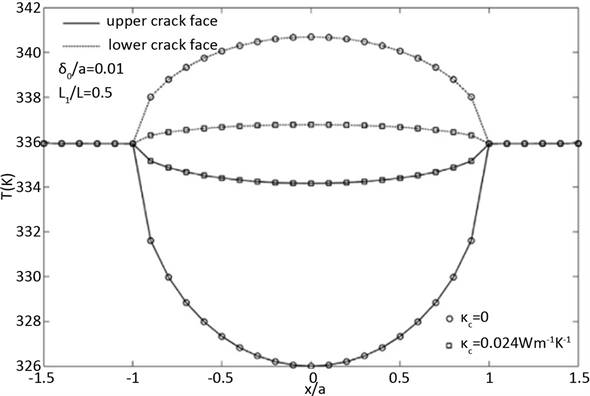
Figure 3. The temperature field on the crack surface and the lamellar thermoelectric materials of the crack extension line which the length is a
图3. 裂纹面上的温度场和裂纹延伸线为a的层状热电材料
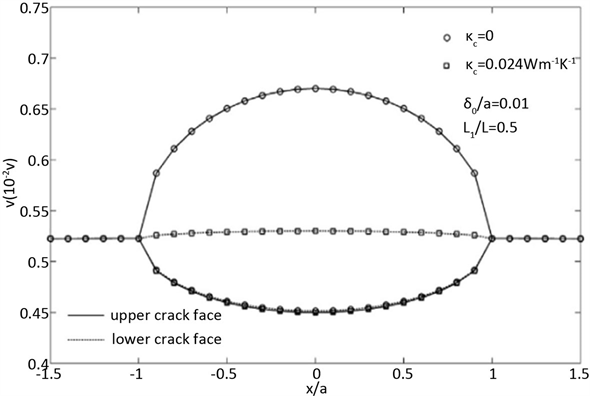
Figure 4. The electric potential field on the crack surface and the lamellar thermoelectric materials of the crack extension line which the length is a
图4. 裂纹面上的电势场和裂纹延伸线为a的层状热电材料
帖效应。证明了由于电子和热通量的耦合,离散化材料中可变温度的参数和表示电子所带热能的对流型为非线性 [40] 。Clin等人通过数值模拟讨论了在不同温度下沿着器件同一方向上各热电偶的应力分布现象,发现热、冷端的温差越大相应的应力也就越大 [41] 。Turenne等人通过数值模拟探讨了热电器件的边界条件、热电偶长度对器件应力分布的影响,利用有限元分析法指出了用两个刚性板将模型固定将会增加热电偶上的冯米赛斯应力,同时发现若热电偶越短,则热梯度也就越高,从而在热电偶连接处产生的应力也就越大 [42] ,在这之后用同样的方法评估了TE材料性能对模块中的热梯度产生的机械应力水平的影响 [43] 。
杨利娜用有限元分析软件ANSYS数值模拟了单边裂纹的脉冲放电过程,得出了脉冲放电后裂纹尖端的温度场及应力场,并计算出了放电前后不同长度裂纹的尖端应力强度因子,证明了脉冲放电可以减小裂纹尖端的应力强度因子,通过减小裂纹的扩展速率,可以抑制裂纹的继续扩展 [44] 。Chen和Lee提出了一种瞬态模拟模型,研究了脉冲热功率对发电机热性能和电性能的影响 [45] 。Wang利用有限元模型研究非线性热电耦合场在热电材料中的应用。采用有限差分法解决时间依赖的响应,根据温度场就可以进行热应力分析、标准热弹性分析和有限元分析 [46] 。
求解热应力对于预测微电子器件可靠性和防止一般的故障也至关重要 [47] 。只有知道设备中的热应力才能对薄膜热电装置的热机械可靠性进行评估。因为在工作条件下薄膜结构严格受到热梯度的影响 [48] 。与有限元法和其他数值方法相比,材料模型具有其显著优点并且仍然可以为设计提供合理的结果 [49] 。使用已有的热电装置去预防热应力的破坏 [50] 。热电材料是一种具有大的热功率,低电阻率和低导热率的材料 [51] 。热冲击可导致脆性热电材料中的微裂纹损伤累积,微裂纹可以影响热电性能和机械完整性 [52] 。张等人在建立热裂缝热电材料板的热冲击模型后,通过数值方法研究耐热冲击性。发现应力强度因子和耐热冲击性对材料的尺寸敏感,应力强度因子随着板厚度的增加而变大 [30] 。
5. 热电材料断裂力学的实验研究
在生产和制造热电材料和复合材料时,其内部产生缺陷,若电势和温度不连续以及热电场和应力集中很容易导致机械故障或电击穿。所以对这些缺陷的评估在热电部件的能量转换效率,强度和可靠性方面起着重要作用。在研究热电材料的缺陷问题方面,许多进行的主要是实验研究。Wang等人通过实验模拟在珀尔帖冷却与热传导和热耦合中验证掺杂的单晶硅微冷却器,图5为微冷却器表面的峰值冷却和最大冷却热量 [53] 。
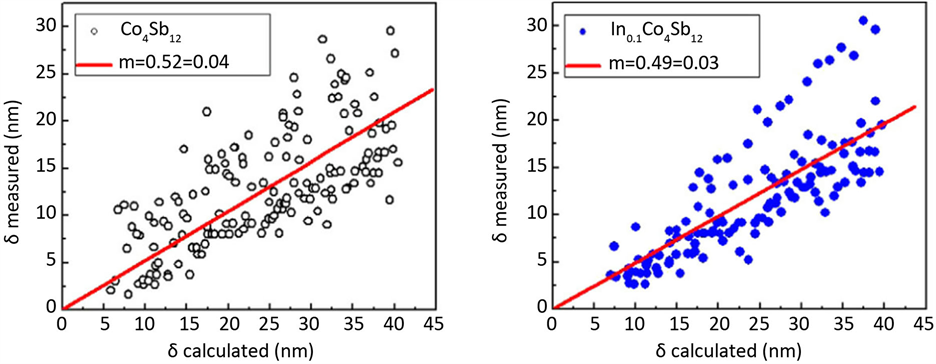
若进行高压烧结热电材料的实验探究,则应考虑材料中残余应力的存在,否则会有裂纹甚至破碎 [54] 。戚德奎等人研究了锌铅热电材料的力学特性受快速急冷法的影响规律,采用熔体旋甩法结合放电等离子烧结技术快速制备了一系列具有高热电性能和高力学强度的锌铅块体材料,并且得到的样品具有极高的抗压强度 [55] 。对热电材料强度的研究是测量断裂韧性的重要指标 [56] 。例如用三点弯曲的方法去测量断裂强度 [57] ,采用脉冲电烧结技术研究热电材料的硬度和断裂韧性,其中高优值归因于高电导率 [58] 。热梯度和热瞬变产生的应力随热电材料的热膨胀系数而变化。通过脉冲电流烧结可以抑制材料膨胀的可能机制 [59] ,减缓裂纹生长的敏感性,使用共振超声波检查材料的硬度和断裂韧性等 [60] 。国内武汉理工大学研究员刘刚对P型Bi2Te3,CoSb10宽温域热电材料结构力学性能进行了研究,对该热电材料的抗折断能力进行了测定,达到了提高材料的抗折强度的目的 [61] 。James同样对热电材料方钴矿CoSb10和In0.1CoSb10的断裂韧性进行了研究分析 [62] 。如图6给出了两种热电材料裂纹尖端韧性数据,结果表明方
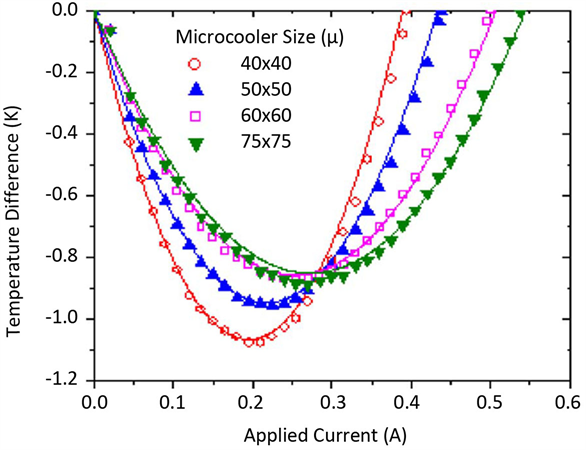
Figure 5. Experiment data on cooling performance of monocrystalline silicon
图5. 单晶硅冷却性能的实验数据
 (a) (b)
(a) (b)
Figure 6. The inherent crack tip toughness data of two materials
图6. 两种材料的固有裂纹尖端韧性数据
钴矿的断裂韧性可以明显低于以前所知的。之后采用维氏显微压痕硬度测试方法分析热电材料的力学性能 [63] 。
威布尔模量是衡量断裂强度的量度,是机械可靠性的指标 [64] 。Kritietal通过实验研究了Cu2Se的机械性能,考虑了裂纹韧性和耐热冲击性 [65] 。结果表明,Cu2Se的断裂韧性值明显高于其他现有热电材料在相同工作温度下的断裂韧性值。
6. 结束语
热电材料断裂力学问题研究具有重要的学术价值和应用前景,属于前沿学科。它涉及到多学科的相互渗透,包括传热学、力学、电学、材料科学等学科。但是由于热电材料的本构方程是非线性的,该领域仍然存在着许多尚未解决的关键问题。作者认为需要进一步研究和发展的方向包括热电材料断裂力学基础理论方面的研究和热电材料结构分析方面的研究。在进行热电材料多场耦合分析和结构设计时,还应该考虑材料的制备以及材料结构成型过程中的工艺力学问题,同时还应该考虑热电材料的损伤检测与性能表征的理论及实验技术,研究解决系统分析软件的开发问题等。在由裂纹引起的热电材料断裂研究中,重点求解应力强度因子。现阶段对热电材料的裂纹问题研究才刚刚开始,例如分析周期裂纹,斜裂纹和多裂纹孔口等问题。在求解热电材料裂纹问题中,建立正交同性或者异性复合材料板的力学模型,求解不同边界条件下的裂纹温度场和电场及应力强度因子。
基金项目
国家自然科学基金项目(11762016),宁夏自然科学研究项目(NZ17009),宁夏高等学校优秀轻年培育项目(NGY2017002)。
文章引用
刘庆楠,丁生虎. 热电材料断裂力学的若干进展
Some Advances in Fracture Mechanics of Thermoelectric Material[J]. 力学研究, 2018, 07(02): 54-65. https://doi.org/10.12677/IJM.2018.72007
参考文献
- 1. 王超, 张蕊, 杜欣, 等. 新型热电材料综述[J]. 电子科技大学学报, 2017, 46(1): 133-150.
- 2. 范天佑. 断裂理论基础[M]. 北京: 科学出版社, 2003.
- 3. Wu, H.J., Chen, B.Y. and Cheng, H.Y. (2017) The p-n, Conduction Type Transition in Ge-Incorporated Bi 2 Te 3, Thermoelectric Materials. Acta Materialia, 122, 120-129. https://doi.org/10.1016/j.actamat.2016.09.043
- 4. 徐桂英, 葛昌纯. 热电材料的研究和发展方向[J]. 材料导报, 2000, 14(11): 38-41.
- 5. 马秋花, 赵昆渝, 李智东, 等. 热电材料综述[J]. 电工材料, 2004(1): 43-47.
- 6. 缪婷婷, 马维刚, 李震, 等. 一种测量热电材料塞贝克系数的新方法[J]. 工程热物理学报, 2011, 32(4): 629-633.
- 7. Jaumot, F.E. (1958) Thermoelectric Effects. Proceedings of the IRE, 46, 538-554. https://doi.org/10.1109/JRPROC.1958.286827
- 8. 任尚芬, 程伟. 能源效率、热电效应和纳米技术[J]. 物理, 2007, 36(9): 673-675.
- 9. Hicks, L.D., Harman, T.C. and Dresselhaus, M.S. (1993) Use of Quantum-Well Superlattices to Obtain a High Figure of Merit from Nonconventional Thermoelectric Materials. Applied Physics Letters, 63, 3230-3232. https://doi.org/10.1063/1.110207
- 10. Jin, Z.H. and Wallace, T.T. (2014) Functionally Graded Thermoelectric Materials with Arbitrary Property Gradations: A One-Dimensional Semianalytical Study. Journal of Electronic Materials, 44, 1-6.
- 11. Fengrong, Y.U., Chen, S., Liu, W., et al. (2012) Current Studies and Perspective of Bi_2Te_3 Thermoelectric Materials. Journal of Yanshan University, 32, 525-540.
- 12. Li, S., Li, X., Ren, Z.F., et al. (2018) Recent Progress on High Performance of Tin Chalcogenides Thermoelectric Materials. Journal of Materials Chemistry A, 6, 2432-2448. https://doi.org/10.1039/C7TA09941J
- 13. Zhang, A.B., Wang, B.L., Wang, J., et al. (2017) Effect of Cracking on the Thermoelectric Conversion Efficiency of Thermoelectric Materials. Journal of Applied Physics, 121, Article ID: 045105. https://doi.org/10.1063/1.4974848
- 14. Today, P. (2007) New High-Efficiency Thermoelectric Material Achieved by Cracking the Crystal. Journal of AIP, 336-338, 842-845.
- 15. Wang, Y.Z. (2015) Effective Material Properties of Thermoelectric Composites with Elliptical Fibers. Applied Physics A, 119, 1081-1085. https://doi.org/10.1007/s00339-015-9072-9
- 16. 宿太超. 高性能热电材料的高温高压合成研究[D]: [博士学位论文]. 长春: 吉林大学, 2009.
- 17. 程靳, 赵树山. 断裂力学[M]. 北京: 科学出版社, 2006.
- 18. 康颖安. 断裂力学的发展与研究现状[J]. 湖南工程学院学报: 自然科学版, 2014, 16(24): 39-42.
- 19. Song, H.P. and Li, C.F.G.J. (2015) Two-Dimensional Problem of a Crack in Thermoelectric Materials. Journal of Thermal Stresses, 38, 325-337. https://doi.org/10.1080/01495739.2015.1015369
- 20. Zhang, A.B. and Wang, B.L. (2013) Crack Tip Field in Thermoelectric Media. Theoretical & Applied Fracture Mechanics, 66, 33-36. https://doi.org/10.1016/j.tafmec.2013.11.006
- 21. Zhang, A.B. and Wang, B.L. (2016) Explicit Solutions of an Elliptic Hole or a Crack Problem in Thermoelectric Materials. Engineering Fracture Mechanics, 151, 11-21. https://doi.org/10.1016/j.engfracmech.2015.11.013
- 22. Zhang, A.B., Wang, B.L., Wang, J., et al. (2017) Thermodynamics Analysis of Thermoelectric Materials: Influence of Cracking on Efficiency of Thermoelectric Conversion. Applied Thermal Engineering, 127, 1442-1450. https://doi.org/10.1016/j.applthermaleng.2017.08.154
- 23. Zeleke, M.A., Xin, L. and Liu, L.S. (2017) Bond Based Peridynamic Formulation for Thermoelectric Materials. Materials Science Forum, 51-59. https://doi.org/10.4028/www.scientific.net/MSF.883.51
- 24. Wang, P. and Wang, B.L. (2017) Thermoelectric Fields and Associated Thermal Stresses for an Inclined Elliptic Hole in Thermoelectric Materials. International Journal of Engineering Science, 119, 93-108. https://doi.org/10.1016/j.ijengsci.2017.06.018
- 25. Lee, E.P., Hsia, S.H., Lin, J.J., et al. (2017) Hemodynamic Analysis of Pediatric Septic Shock and Cardiogenic Shock Using Transpulmonary Thermodilution. Biomed Research International, 2017, Article ID: 3613475. https://doi.org/10.1155/2017/3613475
- 26. Jin, Z.H. (2015) Thermal Stresses in a Multilayered Thin Film Thermoelectric Structure. Microelectronics Reliability, 54, 1363-1368.
- 27. Jin, Z.H., Wallace, T.T., Lad, R.J., et al. (2014) Energy Conversion Efficiency of an Exponentially Graded Thermoelectric Material. Journal of Electronic Materials, 43, 308-313. https://doi.org/10.1007/s11664-013-2868-5
- 28. Liu, Y., Wang, B.L. and Zhang, C. (2016) Thermoelastic Behavior of a Thermoelectric Thin-Film Attached to an Infinite Elastic Substrate. Philosophical Magazine, 97, 43-57.
- 29. 郭亚博. 热电材料热冲击阻力性能的研究[D]: [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2015.
- 30. Wang, B.L., Guo, Y.B. and Zhang, C.W. (2016) Cracking and Thermal Shock Resistance of a Bi2Te3, Based Thermoelectric Material. Engineering Fracture Mechanics, 152, 1-9. https://doi.org/10.1016/j.engfracmech.2015.12.005
- 31. Huang, M.J., Chou, P.K. and Lin, M.C. (2006) Thermal and Thermal Stress Analysis of a Thin-Film Thermoelectric Cooler under the Influence of the Thomson Effect. Sensors and Actuators A: Physical, 126, 122-128. https://doi.org/10.1016/j.sna.2005.10.006
- 32. Hikage, Y., Masutani, S., Sato, T., et al. (2007) Thermal Expansion Properties of Thermoelectric Generating Device Component. 26th International Conference on Thermoelectrics Proceedings, Jeju, 3-6 June 2007, 331-335. https://doi.org/10.1109/ICT.2007.4569489
- 33. Ravi, V., Firdosy, S., Caillat, T., et al. (2009) Thermal Expansion Studies of Selected High-Temperature Thermoelectric Materials. Journal of Electron Materials, 38, 1433-1442. https://doi.org/10.1007/s11664-009-0734-2
- 34. Chuan-Bin, Y.U. and Gao, C.F. (2016) Analysis of a Circular Arc-Crack in Thermoelectric Media. 207-212.
- 35. Song, H.P. and Song, K. (2016) Electric and Heat Conductions across a Crack in a Thermoelectric Material. Journal of Theoretical & Applied Mechanics, 46, 83-98. https://doi.org/10.1515/jtam-2016-0006
- 36. Zhang, A.B. and Wang, B.L. (2013) Applicability of the Crack Faces Thermoelectric Boundary Conditions for Thermopiezoelectric Materials. Mechanics Research Communications, 52, 19-24. https://doi.org/10.1016/j.mechrescom.2013.06.004
- 37. Zang, A.B. and Wang, B.L. (2016) Temperature and Electric Potential Fields of an Interface Crack in a Layered Thermoelectric or Metal/Thermoelectric Material. International Journal of Thermal Sciences, 104, 396-403. https://doi.org/10.1016/j.ijthermalsci.2016.01.023
- 38. Ding, S.H., Zhou, Y.T. and Li, X. (2014) Interface Crack Problem in Layered Orthotropic Materials under Thermo-Mechanical Loading. International Journal of Solids & Structures, 51, 4221-4229. https://doi.org/10.1016/j.ijsolstr.2014.08.007
- 39. Ding, S.H. and Li, X. (2015) Thermoelastic Analysis of Nonhomogeneous Structural Materials with an Interface Crack under Uniform Heat Flow. Elsevier Science Inc., New York.
- 40. Perez-Aparicio, J.L., Taylor, R.L. and Gavela, D. (2007) Finite Element Analysis of Nonlinear Fully Coupled Thermoelectric Materials. Computational Mechanics, 40, 35-45. https://doi.org/10.1007/s00466-006-0080-7
- 41. Clin, T., Turenne, S., Vasilevskiy, D., et al. (2009) Numerical Simulation of the Thermomechanical Behavior of Extruded Bismuth Telluride Alloy Module. Journal of Electronic Materials, 38, 994-1001. https://doi.org/10.1007/s11664-009-0756-9
- 42. Turenne, S., Clin, T.H., Vasilevskiy, D., et al. (2010) Finite Element Thermomechanicial Modeling of Large Area Thermoelectric Generators Based on Bismuth Telluride Alloys. Journal of Electronic Materials, 39, 1926-1933. https://doi.org/10.1007/s11664-009-1049-z
- 43. Picard, M., Turenne, S. and Masut, R.A. (2013) Numerical Simulation of Performance and Thermomechanical Behavior of Thermoelectric Modules with Segmented Bismuth-Telluride-Based Legs. Journal of Electronic Materials, 42, 2343-2349. https://doi.org/10.1007/s11664-012-2435-5
- 44. 杨利娜. 单边裂纹电磁热止裂强化对比研究及裂纹扩展实验方法[D]: [硕士学位论文]. 秦皇岛: 燕山大学, 2013.
- 45. Chen, L.S. and Lee, J.Y. (2015) Effect of Pulsed Heat Power on the Thermal and Electrical Performances of a Thermoelectric Generator. Applied Energy, 150, 138-149. https://doi.org/10.1016/j.apenergy.2015.04.009
- 46. Wang, B.L. (2017) A Finite Element Computational Scheme for Transient and Nonlinear Coupling Thermoelectric Fields and the Associated Thermal Stresses in Thermoelectric Materials. Applied Thermal Engineering, 110, 136-143. https://doi.org/10.1016/j.applthermaleng.2016.08.115
- 47. Li, J.F., Pan, Y., Wu, C.F., et al. (2017) Processing of Advanced Thermoelectric Materials. Scientia Sinica Technologica, No. 9, 1-18.
- 48. Suhir, E. (2013) Could Electronics Reliability Be Predicted, Quantified and Assured. Microelectronics Reliability, 53, 925-936. https://doi.org/10.1016/j.microrel.2013.03.011
- 49. Ni, J.E. and Case, E.D. (2013) Thermal Fatigue of Cast and Hot-Pressed Lead-Antimony-Silver-Tellurium (LAST) Thermoelectric Materials. Journal of Electronic Materials, 42, 1382-1388. https://doi.org/10.1007/s11664-012-2254-8
- 50. Fukada, Y. (2010) Thermoelectric Element and Thermoelectric Module. US 20100059096 A1.
- 51. Pierce, J. and Vaudo, R.P. (2010) Methods of Depositing Epitaxial Thermoelectric Films Having Reduced Crack and/or Surface Defect Densities and Related Devices. WO, US 7804019 B2.
- 52. Jayaram, V., Shivakumara, C., Satyanarayana, M., et al. (2012) Study of the Stability of Na0.7CoO2 Thermoelectric Materials under Shock Dynamic Loading in a Shock Tube.
- 53. Wang, P., Barcohen, A., Yang, B., et al. (2006) Analytical Modeling of Silicon Thermoelectric Microcooler. Journal of Applied Physics, 100, Article ID: 014501. https://doi.org/10.1063/1.2211328
- 54. 乐群. 高压烧结热电材料残余应力分析与数值模拟[D]: [硕士学位论文]. 武汉: 武汉理工大学, 2008.
- 55. 戚德奎, 鄢永高, 李涵, 等. 快速急冷法对β-Zn4+xSb3材料热电及力学性能的影响[J]. 无机材料学报, 2010, 25(6): 603-609.
- 56. Case, E.D. (2006) Weibull Analysis of the Biaxial Fracture Strength of a Cast p-Type LAST-T Thermoelectric Material. Philosophical Magazine Letters, 86, 673-682. https://doi.org/10.1080/09500830600962720
- 57. Yoneda, S., Ohno, Y., Isoda, Y., et al. (2009) Mechanical Properties of PbTe Thermoelectric Materials by Three-Point Bending Fracture Strength Test. Journal of the Society of Materials Science Japan, 46, 174-177.
- 58. Gao, P., Berkun, I., Schmidt, R.D., et al. (2014) Transport and Mechanical Properties of High-ZT, Mg2.08Si0.4−x, Sn0.6Sbx, Thermoelectric Materials. Journal of Electronic Materials, 43, 1790-1803. https://doi.org/10.1007/s11664-013-2865-8
- 59. Ni, J.E., Case, E.D., Schmidt, R.D., et al. (2013) The Thermal Expansion Coefficient as a Key Design Parameter for Thermoelectric Materials and Its Relationship to Processing-Dependent Bloating. Journal of Materials Science, 48, 6233-6244. https://doi.org/10.1007/s10853-013-7421-7
- 60. Schmidt, R.D., Case, E.D., Iii, J.G., et al. (2012) Room-Temperature Mechanical Properties and Slow Crack Growth Behavior of Mg2Si Thermoelectric Materials. Journal of Electronic Materials, 41, 1210-1216. https://doi.org/10.1007/s11664-011-1879-3
- 61. 刘刚. Bi2Te3或CoSb3宽温域热电材料的制备界面结构和力学性能[D]: [硕士学位论文]. 武汉: 武汉理工大学, 2012: 1-15.
- 62. Eilertsen, J., Subramanian, M.A. and Kruzic, J.J. (2013) Fracture Toughness of Co4Sb12 and In0.1Co4Sb12 Thermoelectric Skutterudites Evaluated by Three Methods. Journal of Alloys and Compounds, 552, 492-498. https://doi.org/10.1016/j.jallcom.2012.11.066
- 63. Ma, J.M., Firdosy, S.A., Kaner, R.B., et al. (2014) Hardness and Fracture Toughness of Thermoelectric La3−xTe4. Journal of Materials Science, 49, 1150-1156. https://doi.org/10.1007/s10853-013-7794-7
- 64. Fan, X. (2013) Mechanical Characterization of Hydroxyapatite, Thermoelectric Materials and Doped Ceria.
- 65. Tyagi, K., Gahtori, B., Bathula, S., et al. (2015) Crystal Structure and Mechanical Properties of Spark Plasma Sintered Cu2Se: An Efficient Photovoltaic and Thermoelectric Material. Solid State Communications, 207, 21-25. https://doi.org/10.1016/j.ssc.2015.02.004