Software Engineering and Applications
Vol.04 No.03(2015), Article ID:15527,7
pages
10.12677/SEA.2015.43007
Application of Differential Operator and Linear Fitting in Crosshair Center Pinpoint
Bochao Liu, Jian Zhao
Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun Jilin
Email: liubochao@ciomp.ac.cn
Received: Jun. 19th, 2015; accepted: Jun. 22nd, 2015; published: Jun. 26th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In order to satisfy the requirement of crosshair center pinpoint for lens decentration measurement, a crosshair center pinpoint method based on differential operator and linear fitting is proposed. First, the edges of crosshair in both X and Y directions can be obtained by using differential operator to compute the difference in both X and Y directions. Then, two linear equations in both X and Y directions are fitted with orthogonal least square method using the edges obtained. Finally, the intersection point of the two linear equations is used as the crosshair center. Experimental results indicate that the precision of the crosshair center pinpoint is less than one pixel in the images grabbed by the CCD whose resoluntion is 1292 × 964 pixel and pixel size is 3.75 μm × 3.75 μm and the precision of pinpoint is less than 2 μm in lens decentration measurement. It can satisfy the system requirements of non-contact, online, real time, higher precision and rapid speed, as well as strong anti-jamming and stabilization.
Keywords:Crosshair Center, Differential Operator, Linear Fitting, Sub-Pixel
微分算子和直线拟合在十字丝中心定位中的应用
刘博超,赵建
中国科学院长春光学精密机械与物理研究所,吉林 长春
Email: liubochao@ciomp.ac.cn
收稿日期:2015年6月19日;录用日期:2015年6月22日;发布日期:2015年6月26日

摘 要
为了满足镜头中心偏差测量中十字丝中心精确定位的要求,本文提出了一种基于微分算子和直线拟合的十字丝中心定位方法。根据十字丝成像的特殊性,首先,使用微分算子分别在X方向和Y方向求差分得到十字丝X方向和Y方向的边缘。接着,采用正交最小二乘法将刚刚得到的X方向和Y方向的边缘分别拟合为X方向和Y方向上的两条直线方程。最后,计算两条拟合直线的交点作为十字丝的中心。实验结果表明:在分辨率为1292 × 964像元为3.75 μm × 3.75 μm的CCD采集到的图像中十字丝中心的定位精度小于1个像素,在镜头中心偏差测量过程中其定位精度小于2 μm。基本满足镜头中心偏差测量对十字丝中心定位精度高、抗干扰能力强、重复性好等要求。
关键词 :十字丝中心,微分算子,直线拟合,亚像素

1. 引言
图像测量[1] 技术是近年来在测量领域中新兴的一种高性能测量技术。它以光学技术为基础,将光电子学、计算机技术、激光技术、图像处理技术等多种现代科学技术融合为一体,构成光、机、电、算综合体的测量系统。所谓的图像测量,就是把测量对像图像当作检测和传递信息的手段或载体加以利用的精确测量技术,是一种结合视频图像和计算机识别的图像处理技术,是测量被测对象时把图像当作检测和传递的手段或载体加以利用的测量方法,其目的是从图像中提取有用的信号。它通过对于获得的二维图像进行处理和分析,得到需要的三维场景的信息,最终实现测量的目的。目前视频图像的测量理论还没有通用的方法和算法,针对不同测量对象和条件,要研究不同的实用方法和算法。图像测量技术广泛应用于智能交通、安防、工业产品质量检测等各个领域,并且随着计算机技术和信息技术的发展,其实现方法和手段也将日新月异。
由于十字丝[2] 成像的特殊性,其经常被作为传递信息的载体用于图像测量技术之中。基于反射式的光学镜头中心偏差测量系统[3] 是一种光学镜头辅助装调设备[4] ,其工作过程为:将光源产生的十字丝聚焦在被测镜面的球心相对于其上所有镜面成像的像点上,通过反射成像在CCD上,旋转转台记录十字丝在CCD上成像的运动轨迹,将运动轨迹的零点位置和由运动轨迹拟合出的圆的直径作为两个重要参数代入光学公式中进行计算。因此,是否能够准确地定位十字丝中心的位置对整个光学镜头中心偏差测量系统的精度有着重要的影响。
本文针对十字丝成像正交性的特点,提出了一种结合微分算子[5] 和直线拟合[6] 定位十字丝中心的方法,即首先使用微分算子分别在X方向和Y方向求差分得到十字丝X方向和Y方向的边缘,然后采用正交最小二乘法将得到的X方向和Y方向的边缘拟合为X方向和Y方向上的两条直线方程,最后计算两条拟合直线的交点作为十字丝的中心坐标。实验结果表明,该方法具有良好的重复性,定位精度可以达到亚像素级[7] ,基本满足镜头中心偏差测量对十字丝中心定位[8] 精度高的要求。
2. 微分算子提取垂直边缘和水平边缘
对于离散的数字图像来说,一元函数f(x)一阶微分可以定义为差分形式:
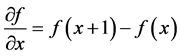
而对于一幅二维数字图像而言,X方向和Y方向上的一阶微分可以分别定义为:
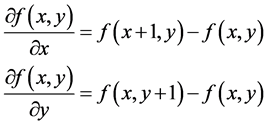
参照常用的Roberts算子、Prewitt算子、Sobel算子[9] 等边缘检测[10] 算子的定义,我们可以定义如图1所示的垂直算子和水平算子用于提取十字丝的垂直边缘和水平边缘。
在光学镜头中心偏差测量系统中使用的分辨率为1292 × 964的CCD采集到的实时显示的十字丝图像如图2所示。
的十字丝垂直边缘和水平边缘如图3所示。图3仅为中间输出结果的示意图,在实际应用的过程中只需保存垂直方向结果的x、y坐标以及水平方向结果的x、y坐标用于接下来的直线拟合即可。
3. 最小二乘直线拟合
3.1. 经典的最小二乘直线拟合
经典的最小二乘直线拟合如图4所示,其基本过程为:

Figure 1. Vertical operator and horizontal operator 图1. 垂直算子和水平算子
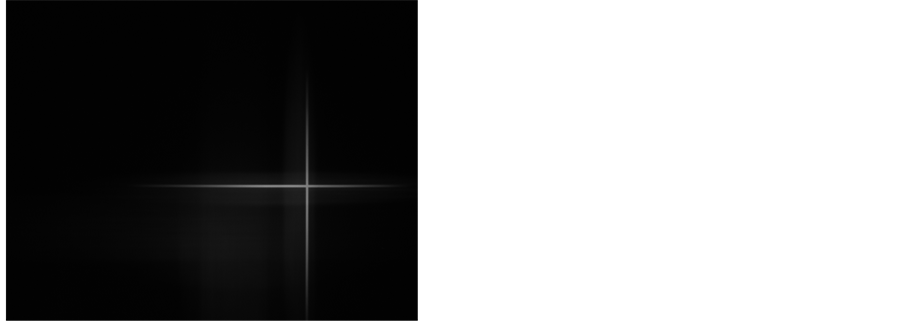
Figure 2. Real-time image of crosshair 图2. 实时的十字丝图像

Figure 3. Schematic diagram of horizontal and vertical edge 图3. 垂直和水平边缘示意图

Figure 4. Classical least square linear fitting 图4. 经典最小二乘直线拟合
1) 假设拟合后的直线方程为y = kx + b,其中k为斜率,b为截距,是最终要求的两个量;
2) 假定任意一点的x坐标xi是准确的,求使得 取得最小值时的k和b;
取得最小值时的k和b;
3) 根据2中的要求,应有 成立;
成立;
4) 解3中的方程可得:

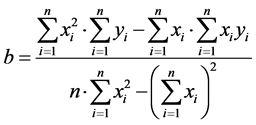
3.2. 正交的最小二乘直线拟合
在经典的最小二乘直线拟合过程中假定任意一点的x坐标xi是准确的,然而在系统中得到的十字丝边缘的x、y坐标都是随机的,因此我们考虑使用如图5所示的正交的最小二乘[11] 直线拟合方法,以任意一点到拟合直线的距离为参考标准拟合X方向和Y方向的两条直线,其基本过程为:1) 假设拟合后的直线方程为y = kx + b,其中k为斜率,b为截距,是最终要求的两个量;

Figure 5. Orthogonal least square linear fitting 图5. 正交最小二乘直线拟合
2) 计算任意一点(xi, yi)到直线y = kx + b的距离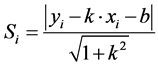 ;
;
3) 求使得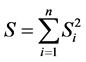 取得最小值时的k和b;
取得最小值时的k和b;
4) 根据3中的要求同样应有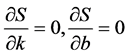 成立,即
成立,即

5) 解4中的方程可得:

其中,
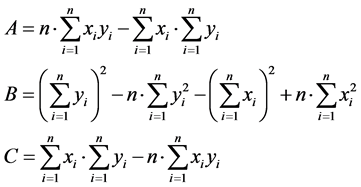
解得的竖直方向和水平方向直线方程各有两组解,在拟合竖直方向直线方程时取k的绝对值较大的一组解,在拟合水平方向直线方程时取k的绝对值较小的一组解。
4. 测量实验与结果
为了验证本文提出方法的精度和重复性,我们将被测镜头固定后在光学镜头中心偏差测量系统上进行了实验,相机采用分辨率为1292 × 964、像元尺寸为3.75 μm × 3.75 μm的CCD。表1为将CCD曝光时间设置为25 ms,每隔10帧采集一次,用本文提出的方法计算10次十字丝中心位置得到的测量结果。
从表1列出的实验结果可以看出,在同一位置计算得到的十字丝中心最大位置和最小位置间的距离小于1个像素,能够达到亚像素级[12] ,多次测量的结果之间小于2 μm,具有较高的重复定位精度。
为了验证本文提出方法对光照的抗干扰能力,我们将被测镜头固定后分别在不同的曝光时间下采集到的图像如图6所示,表2为在不同曝光时间下计算得到的十字丝中心位置。



 (a) 10 ms (b) 15 ms (c) 20 ms (d) 25 ms
(a) 10 ms (b) 15 ms (c) 20 ms (d) 25 ms


 (e) 30 ms (f) 35 ms (g) 40 ms (h) 45 ms
(e) 30 ms (f) 35 ms (g) 40 ms (h) 45 ms
Figure 6. Images of different exposure time 图6. 不同曝光时间图像
从表2列出的实验结果可以看出,在同一位置不同曝光时间下计算得到的十字丝中心最大位置和最小位置间的距离也小于1个像素,同样能够达到亚像素级,多次测量的结果之间小于2 μm,对光照强度的变化具有较高的抗干扰能力。
5. 结论
本文根据光学镜头中心偏差测量系统检测精度高的要求并针对十字丝成像的特点,提出了一种结合微分算子和直线拟合定位十字丝中心的方法,并将该方法应用于光学镜头中心偏差测量系统中。首先提取垂直和水平方向的边缘,然后拟合两个方向的直线方程,最后计算两条直线方程的交点作为十字丝中心位置。实验结果证明:在光学镜头中心偏差测量系统中采用的分辨率为1292 × 964像元为3.75 μm × 3.75 μm的CCD采集到的图像中,十字丝中心的定位精度小于1个像素,在镜头中心偏差测量过程中其定位精度小于2 μm。基本满足镜头中心偏差测量对十字丝中心定位精度高、抗干扰能力强、重复性好的要求。
文章引用
刘博超,赵建, (2015) 微分算子和直线拟合在十字丝中心定位中的应用
Application of Differential Operator and Linear Fitting in Crosshair Center Pinpoint. 软件工程与应用,03,51-58. doi: 10.12677/SEA.2015.43007
参考文献 (References)
- 1. 陶李, 王珏, 邹永宁 (2012) 改进的Zernike矩工业CT图像边缘检测.中国光学, 1, 48-56.
- 2. 杜飞明, 廖兆曙, 张桂林 (2007) 一种十字丝中心坐标检测方法. 计算技术与自动化, 3, 81-85.
- 3. 郭帮辉 (2014) 基于镜面间隔和中心偏差测量的光学镜头辅助装调设备的研究. 博士论文, 中国科学院大学, 北京.
- 4. 赵阳, 巩岩 (2012) 投影物镜小比率模型的计算机辅助装调. 中国光学, 4, 94-400.
- 5. 丁畅 (2014) 图像处理的偏微分方程方法研究. 硕士论文, 大连海事大学, 大连.
- 6. 姚宜斌, 黄书华, 孔建 (2014) 空间直线拟合的整体最小二乘算法. 武汉大学学报(信息科学版), 5, 571-574.
- 7. 刘国栋, 刘炳国, 陈凤栋 (2009) 亚像素定位算法精度评价方法的研究. 光学学报, 12, 3446-3451.
- 8. 王林波, 王延杰, 邸男 (2014) 基于几何特征的圆形标志点亚像素中心定位. 液晶与显示, 6, 1003-1009.
- 9. Rafael, C.G., Richard, E.W., 著, 阮秋琦, 阮智宇, 译 (2005) Digital image processing. 2nd Edition, 电子工业出版社, 北京.
- 10. 赵慧, 刘建华, 梁俊杰 (2014) 5种常见边缘检测方法的比较分析. 现代电子技术, 6, 89-92.
- 11. 刘道华, 张礼涛, 曾召霞 (2013) 基于正交最小二乘法的径向基神经网络模型. 信阳师范学院学报(自然科学版), 3, 428-431.
- 12. 陈阔, 冯华君, 徐之海 (2013) 亚像素精度的行星中心定位算法. 光学精密工程, 7, 1881-1890.
