Dynamical Systems and Control
Vol.05 No.03(2016), Article ID:18026,9
pages
10.12677/DSC.2016.53011
A New Method Based on Groebner Bases for Solving the Beckmann Traffic Equilibrium Assignment Model
Xianpeng Wei1, Qiuyan Zhan2, Lu Chao2
1College of Transportation, Shanghai Maritime University, Shanghai
2College of Art and Science, Shanghai Maritime University, Shanghai

Received: Jun. 26th, 2016; accepted: Jul. 16th, 2016; published: Jul. 20th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Beckmann traffic equilibrium assignment model is the basis of the study of traffic assignment problem. However, at present, the solution of Beckmann traffic equilibrium assignment model is still dependent on the F-W iterative algorithm and intelligent optimization methods, which can’t obtain the exact solution. In order to find the exact solution of the Beckmann traffic equilibrium assignment model, this paper uses the advantage of Groebner bases theory in solving multidimensional polynomial equations, transforms the Beckmann model into a polynomial equation, then introduces the new variables and mapping to make the general polynomial into monomial, and then a method for solving the traffic equilibrium assignment model of Beckmann exactly is given. Finally, an example is given to show the effectiveness of the proposed method.
Keywords:Traffic Engineering, Traffic Equilibrium Assignment, Beckmann, Groebner Bases

基于Groebner基的Beckmann交通平衡分配模型新解法
魏贤鹏1,战秋艳2,朝鲁2
1上海海事大学交通运输学院,上海
2上海海事大学文理学院,上海

收稿日期:2016年6月26日;录用日期:2016年7月16日;发布日期:2016年7月20日

摘 要
Beckmann交通平衡分配模型是研究交通分配问题的基础,然而目前该模型的求解主要依赖于F-W迭代算法和智能优化算法,无法求得精确解。为了寻找Beckmann交通平衡分配模型的精确解,本文借助Groebner基理论在求解多维多项式方程方面的优势,将Beckmann模型转化为多项式方程,通过引入新的变量和映射将一般多项式转化为单项式,给出了精确求解Beckmann交通平衡分配模型的方法。最后给出算例验证了该方法的有效性。
关键词 :交通工程,交通平衡分配,Beckmann,Groebner基

1. 引言
交通流分配是交通需求四阶段预测的最后阶段,是实现交通规划设计的关键一步,其目的就是将预测得到的OD交通量,根据已知道路网的描述,按照一定的规则符合实际的分配到路网中的各条道路上去,进而求出路网中各路段的交通量、所产生的OD费用矩阵,并根据城市交通网络的使用状况作出分析和评价 [1] 。然而要实现交通量符合实际地分配到道路网络中并非易事,目前许多交通分配模型是建立在Wardrop第一原理概念上的,最具代表性的模型是1956年著名学者Beckmann提出的描述Wardrop第一原理的数学规划模型。Beckmann模型涉及维数多,且是一个非线性规划模型,求解该模型成为一个难题,直到1975年LeBlanc等学者将Frank-Wolfe算法用于求解Beckmann模型,简称F-W解法,该方法是用线性规划逐步逼近非线性的方法,是一种迭代法。在每步迭代中,先找到目标函数最速下降方向,然后再找到一个最优步长,在最速下降方向上截取最优步长得到下一步迭代起点,重复迭代直到找到最优解为止 [2] 。为处理实际中的大规模网络问题,许多学者将智能进化方法应用到交通分配模型求解中,如神经网络算法 [3] 、遗传算法 [4] - [6] 、蚂蚁算法 [7] 、启发式算法 [8] [9] 、模拟退火算法 [10] 、免疫克隆退火算法 [11] 、粒子群算法 [12] 等。无论是W-F解法还是智能优化方法,都只能得到模型的近似解,因此寻求模型精确解是交通平衡分配的重要内容。
Groebner基理论的形成最早是在1927年,F. S. Nlacauly在全体单项式组成的集合中引入全序的概念,研究其理想的不变量。直到1965年B. Buchberger利用除法算法系统地研究了域上多元多项式环的理想生成元问题,才可以解决与理想相关的问题。从此,Groebner基的理论及其应用得到快速发展。2002年中南大学陈小松教授成功将Groebner基理论应用到求解最短路径问题中 [13] ,到2007年陈小松教授指导其学生朱玉莲将Groebner基理论应用到机场停车位优化分配中 [14] 。国外学者Serkan Hoten给出了Groebner基理论求解整数规划问题的方法 [15] 。
本文考虑到Beckmann交通平衡分配模型是一个维数较大的凸规划问题或非线性规划问题。借助Groebner基理论在求解多维多项式方程方面的优势,首次将Groebner基理论应用到求解Beckmann交通平衡分配模型上。首先将Beckmann交通平衡分配模型转化为具体的多项式,通过引入新的变量和映射将一般多项式转化为单项式,然后由Grobner基方法求解。
2. 问题的转化及Groebner基方法
由于居民出行的单位是次,组成的交通流量是整数,所以本节介绍有关Groebner基和整数规划的理论。以整数规划问题的标准形式为例简述Groebner基理论。
标准形式:
满足约束条件
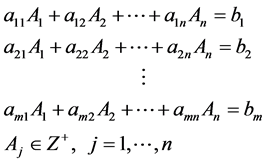 (1)
(1)
其中, 是非负整数集,
是非负整数集,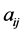 是已知的常数,
是已知的常数,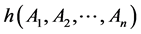 表示与变量
表示与变量 有关的函数。其简写形式为:
有关的函数。其简写形式为:
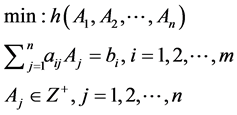 (2)
(2)
本文把以上问题转化为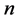 元多项式的问题,从而用多元多项式理论和方法求解。先给出本文用到的关于多元多项式
元多项式的问题,从而用多元多项式理论和方法求解。先给出本文用到的关于多元多项式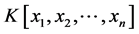 中的基本结论。
中的基本结论。
定义1 [14] 设K表示一个域,对于任意的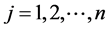 ,定义映射
,定义映射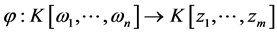 为
为
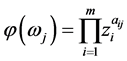
且对于一般的多项式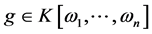 ,定义
,定义 。因为对可行域的整数点
。因为对可行域的整数点 ,及单项式
,及单项式 有
有
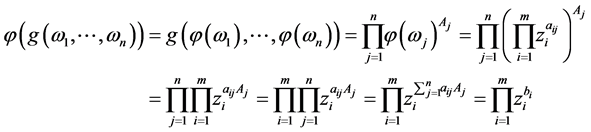
综上推倒定义1将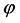 的单项式
的单项式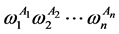 映射到
映射到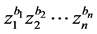 ,从而映射
,从而映射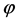 建立了优化问题(2)的等式两边的关系。
建立了优化问题(2)的等式两边的关系。
定义2 [14] 假若给定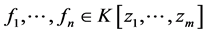 ,固定
,固定 上单项式的顺序使具有如下性质:任一含有某个
上单项式的顺序使具有如下性质:任一含有某个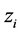 的单项式大于任一含仅有
的单项式大于任一含仅有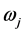 的单项式。设
的单项式。设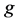 是下述理想的Groebner基:
是下述理想的Groebner基:
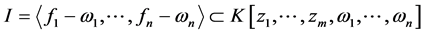 。对于属于
。对于属于 的任意
的任意 ,
,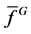 表示
表示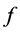 被
被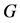 约化的余式。则
约化的余式。则
a) 当且仅当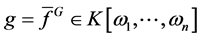 时多项式
时多项式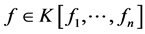 ;
;
b) 如果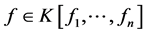 并且
并且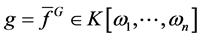 ,那么
,那么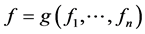 ;
;
c) 如果每个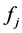 和
和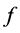 都是单项式而且
都是单项式而且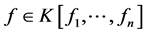 ,那么
,那么 也是单项式。
也是单项式。
定理 [16] 在整数规划问题(2)中,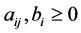 且记
且记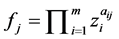 ,设基由
,设基由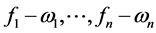 生成的理想记为
生成的理想记为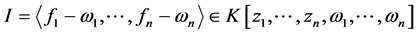 ,并G为I的Groebner基(取合适的单项式序)则当
,并G为I的Groebner基(取合适的单项式序)则当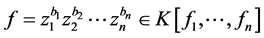 时,
时,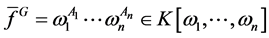 给出整数规划问题(2)的最优解。
给出整数规划问题(2)的最优解。
综上,我们可以得到一个求解整数规划问题(2)的Groebner基算法。
输入:优化问题(2)中的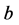 以及由目标函数
以及由目标函数 定义的单项式序>
定义的单项式序>
输出:问题(2)的最优解。
Step1: ;
;
Step2: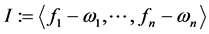 ;计算
;计算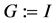 关系序>的Groebner基;
关系序>的Groebner基;
Step3:置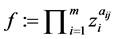 ,计算余式
,计算余式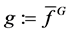 ;
;
Step4:若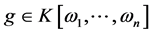 那么输出
那么输出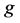 的指数向量,否则无解。
的指数向量,否则无解。
3. Beckmann模型和求解过程
3.1. Beckmann均衡分配模型 [2]
Beckmann均衡分配模型是Wardrop第一原理的数学描述,是研究交通分配问题的基础,具体的模型表达式见式(3)至式(5)。
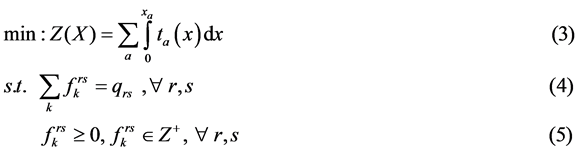
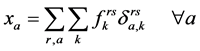
其中,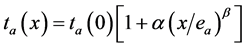 。
。
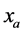 表示路段a上的交通量,它组成的向量为
表示路段a上的交通量,它组成的向量为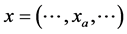 ;
;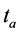 表示路段a的交通阻抗;
表示路段a的交通阻抗;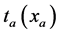 表示路段a的以流量为自变量的阻抗函数;
表示路段a的以流量为自变量的阻抗函数; 表示点对
表示点对 间的第k条路径的交通量,其向量为
间的第k条路径的交通量,其向量为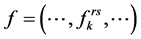 ;
;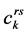 表示点对
表示点对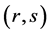 间的第k条路径的阻抗;
间的第k条路径的阻抗;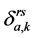 是路段–径路相关变量,即0-1变量,如果路段a属于从出发地r目的地为s的OD间第k条径路,则
是路段–径路相关变量,即0-1变量,如果路段a属于从出发地r目的地为s的OD间第k条径路,则 ,否则
,否则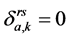 ;
;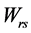 表示点对
表示点对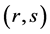 之间的所有径路集合;
之间的所有径路集合;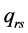 表示点对
表示点对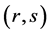 之间的交通量;
之间的交通量;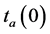 表示车辆平均自由行使时间;
表示车辆平均自由行使时间;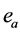 表示路段a的交通容量;
表示路段a的交通容量;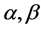 为参数,
为参数, 。
。
3.2. 应用Groebner基理论求解过程
3.2.1. 求解思路
Beckmann模型中路段阻抗与路段中交通量有关,所以组成的路径也是不唯一的,然而Groebner基理论处理的是确定多项式的求解。所以假设每一个OD对之间的所有路径都有可能有交通量产生,当达到平衡时,所有被利用的路径具有相等而最小的阻抗,而未被利用的路径与其具有相等或更大的阻抗。
若 ,必有
,必有 ,说明如果从r到s有两条及以上的径路被选中,那么他们行驶时间相等;若
,说明如果从r到s有两条及以上的径路被选中,那么他们行驶时间相等;若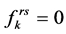 ,必有
,必有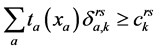 ,说明如果从r到s的径路流量等于零,那么该径路的行驶时间一
,说明如果从r到s的径路流量等于零,那么该径路的行驶时间一
定超过被选中的径路行驶时间。最终约束条件都转换为确定的线性等式,目标函数为多维的非线性函数,应用Groebner基理论求解。
3.2.2. 求解过程
由3.2.1节的分析可将Beckmann模型变为如下形式:
 (6)
(6)
该式中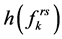 表示目标函数只与变量
表示目标函数只与变量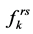 有关的函数。假设从起点r到终点s的所有径路的个数为n。对式(6)中每一个等式引入一个不确定的变量
有关的函数。假设从起点r到终点s的所有径路的个数为n。对式(6)中每一个等式引入一个不确定的变量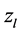 ,并且给以乘幂得到式(7):
,并且给以乘幂得到式(7):
 (7)
(7)
对于任意的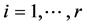 ,
, ,
,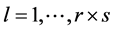 。把等式的左边和右边分别相乘并且重新排列指数,得到等式(8)。
。把等式的左边和右边分别相乘并且重新排列指数,得到等式(8)。
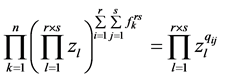 (8)
(8)
由命题1可以得到映射 ,即
,即
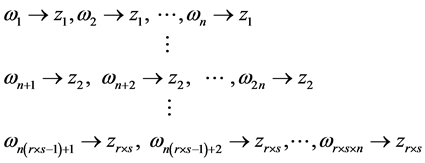
这一问题的可行域内的整数点
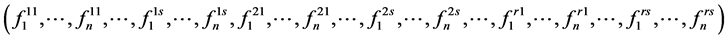 是满足如下条件的点:
是满足如下条件的点:
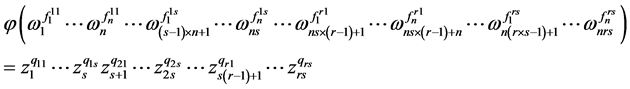
并且在这种情况下,每个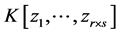 中的单项式是
中的单项式是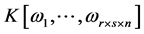 中某单项式的像。
中某单项式的像。
由命题2考虑理想
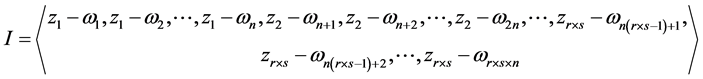 ,并采用下列词典序:
,并采用下列词典序: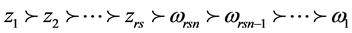 ,就可以得到一个关于理想
,就可以得到一个关于理想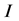 的Groebner基记为G。取
的Groebner基记为G。取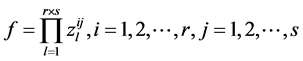 ,求
,求 关于
关于 的约化多项式
的约化多项式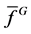 ,记为
,记为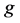 ,如果
,如果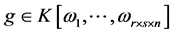 ,那么
,那么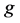 的指数向量就是所要求的模型解,否则问题无解。
的指数向量就是所要求的模型解,否则问题无解。
4. 案例分析
4.1. 算例描述
本文以文献 [9] 中西安湘子庙历史街区慢行网络为例说明该算法的有效性。网络的拓扑结构见图1。各个路段属性数据见表1。
4.2. 求解过程
算例中有四个OD对,每个OD对的流量分别为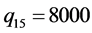 ;
;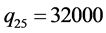 ;
;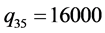 ;
;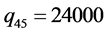 ;其中OD对1-5有四条路径,其他OD对只有一条路径,所有路径对应的路段见表2。
;其中OD对1-5有四条路径,其他OD对只有一条路径,所有路径对应的路段见表2。
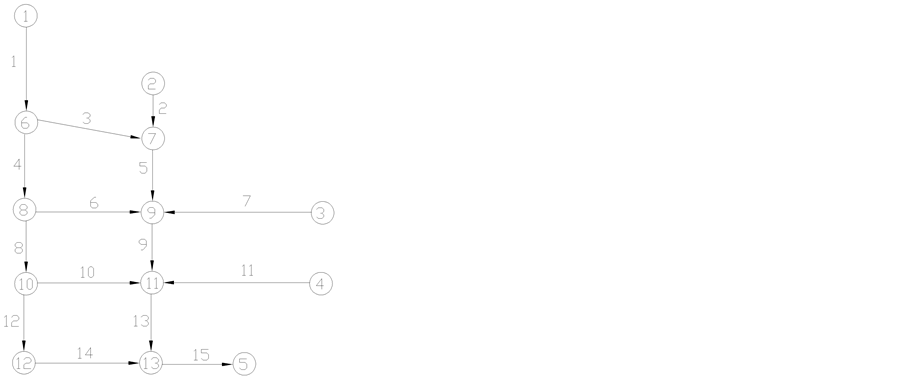
Figure 1. Schematic diagram of road network
图1. 路网示意图
Table 1. Link attribute table
表1. 路段属性表
Table 2. Correspondence relation of path-link
表2. 路径-路段对应关系
将各个路径的流量转换为路段流量,结合表1中路段费用函数代入3.1节中Beckmann模型,整理得到式(9)~(13)。
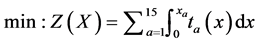 (9)
(9)
 (10)
(10)
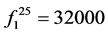 (11)
(11)
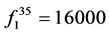 (12)
(12)
 (13)
(13)
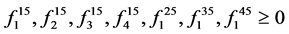
其中,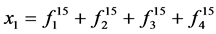 ;
;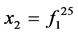 ;
;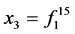 ;
;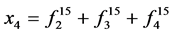 ;
;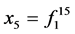 ;
;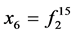 ;
;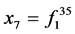 ;
;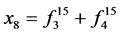 ;
;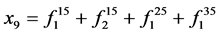 ;
;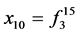 ;
; ;
;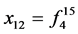 ;
;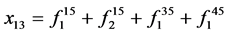 ;
;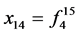 ;
;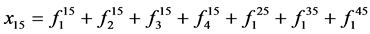 ;
;
将式(10)~(13)中等式约束分别引入变量 ,
,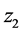 ,
,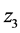 ,
,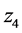 并且两边乘幂得到
并且两边乘幂得到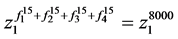 ,
, ,
,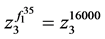 ,
,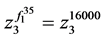 再将三个等式左右两边分别相乘得
再将三个等式左右两边分别相乘得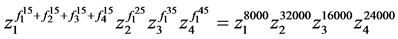 。由命题1得到映射:
。由命题1得到映射:
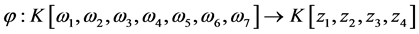
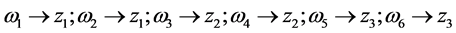
由命题2得到理想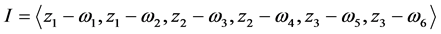 ,根据目标函数定义特定的序,使用Mathematica软件中
,根据目标函数定义特定的序,使用Mathematica软件中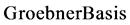 命令得到一组Groebner基G:
命令得到一组Groebner基G:
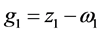
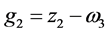
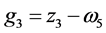


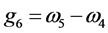
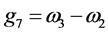
令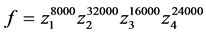 ,由定理2中的算法求得f被G约化的余式
,由定理2中的算法求得f被G约化的余式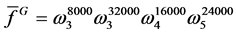 。
。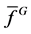 的指数向量对应目标函数的解,即
的指数向量对应目标函数的解,即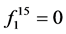 ,
,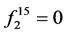 ,
,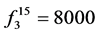 ,
,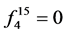 ,
,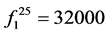 ,
,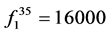 ,
, 。所以平衡后各个路段的流量为:
。所以平衡后各个路段的流量为: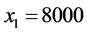 ;
;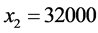 ;
;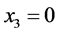 ;
; ;
;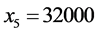 ;
; ;
;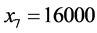 ;
;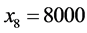 ;
;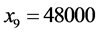 ;
;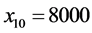 ;
;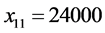 ;
;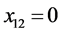 ;
; ;
;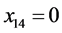 ;
;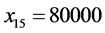 。由计算结果可知,每一个OD对的所有路径中,阻抗较小的路径都分配了流量且行驶时间相等,而阻抗大的路径流量为零,满足Wardrop第一原理,所以Groebner基理论可以用于求解Beckmann模型。与W-F迭代解法和智能优化解法相比,Groebner基理论得到的解是模型的精确解,有更高的精度。然而该方法在面对大规模路网时,由于路径多,目标函数比较复杂,针对目标函数定义特定序的工作量比较大。而对于中小城市路网使用Groebner基理论的方法作交通流量分配更经济。
。由计算结果可知,每一个OD对的所有路径中,阻抗较小的路径都分配了流量且行驶时间相等,而阻抗大的路径流量为零,满足Wardrop第一原理,所以Groebner基理论可以用于求解Beckmann模型。与W-F迭代解法和智能优化解法相比,Groebner基理论得到的解是模型的精确解,有更高的精度。然而该方法在面对大规模路网时,由于路径多,目标函数比较复杂,针对目标函数定义特定序的工作量比较大。而对于中小城市路网使用Groebner基理论的方法作交通流量分配更经济。
5. 结论与展望
Groebner基方法在求解非线性多项式方程方面具有优势,可以从任一多项式理想的一组给定生成元有效计算出另一组良好的生成元(称为Groebner基),且有Hilbert基定理保证得到约化的Groebner基是唯一的,所以求得的解准确可靠。是求解精确解的重要方法。本文结合Groebner基理论将Beckmann模型转化为多项式方程组,给出了精确求解Beckmann模型的新方法,并结合实例验证了该方法的有效性。
然而,该方法是假设每个OD对上的所有路径都有机会分配交通量,这就大大增加了计算机的内存需求,对于OD对较多的路网,路径非常多,需要高性能计算机处理。同时,依据目标函数定义特定的序也是一件庞大的工作。所以如何制定恰当的规则寻找有效路径,使得那些平衡后为零的路径在分配之前就剔除掉,保留下来的路径再用该方法寻找精确解是未来研究的方向。
基金项目
国家自然科学基金委员会资助项目(11571008)。
文章引用
魏贤鹏,战秋艳,朝 鲁. 基于Groebner基的Beckmann交通平衡分配模型新解法
A New Method Based on Groebner Bases for Solving the Beckmann Traffic Equilibrium Assignment Model[J]. 动力系统与控制, 2016, 05(03): 96-104. http://dx.doi.org/10.12677/DSC.2016.53011
参考文献 (References)
- 1. 邵春福. 交通规划原理[M]. 北京: 中国铁道出版社, 2006: 172-180.
- 2. 刘灿齐. 现代交通规划学[M]. 北京: 人民交通出版社, 2001: 206-244.
- 3. 董敬欣, 吴建平. 基于神经网络的交通平衡求解算法[J]. 系统仿真学报, 2005, 17(6): 1380-1383.
- 4. Li, R.M. and Li, W. (2005) The Application of Genetic Algorithm to Dynamic Traffic Assignment. IEEE. Proceedings of Intelligent Vehicles Symposium, Las Vegas, 6-8 June 2005, 827-832.
- 5. 陆化普, 孙煦, 吴娟. 公交专用道优化设计的双层规划模型[J]. 中国路学报, 2015, 28(2): 88-93.
- 6. 刘强, 陆化普, 王庆云. 区域综合交通枢纽布局双层规划模型[J]. 东南大学学报(自然科学版), 2010, 40(6): 1359-1362.
- 7. 徐勋倩, 王亚萍. 用蚂蚁算法处理固定需求交通平衡分配问题[J]. 南通工学院学报: 自然科学版, 2004, 3(2): 24- 27.
- 8. Mahut, M. (2005) A Heuristic Algorithm for Simulation-Based Dynamic Traffic Assignment. Proceedings of IEEE Intelligent Transportation Systems, Vienna, 13-15 September 2005, 239-244.
- 9. 王秋平, 刘星明, 魏华. 历史街区慢行交通连续网络设计鲁棒优化模型[J]. 长安大学学报(自然科学版), 2015, 35(5): 112-116.
- 10. 李宗平, 李冰. 城市交通连续平衡网络设计问题的模拟退火算法[J]. 系统工程, 2004, 22(2): 87-91.
- 11. 孙杨, 宋瑞, 何世伟, 等. 混合交通网络设计及免疫克隆退火算法求解研究[J]. 交通运输系统工程与信息, 2009, 9(3): 103-108.
- 12. 王素欣, 高利, 崔小光, 等. 交通分配的粒子群优化算法[J]. 交通运输工程学报, 2007, 7(5): 97-100.
- 13. 陈小松, 彭丰富. Groebner基理论在最短路径问题中的应用[J]. 中南工业大学学报, 2002, 33(6): 648-650.
- 14. 朱玉莲. Groebner基理论及其在一些优化问题上的应用[D]: [硕士学位论文]. 长沙: 中南大学, 2007: 15-18.
- 15. Hoşten, S. and Sturmfels, B. (2005) Integer Programming and Combinatorial Optimization. Springer-Verlag, New York, Berlin, Heidelberg, 267-270.
- 16. 周梦. 计算机代数与应用[M]. 武汉: 武汉大学出版社, 2002: 205-210.
