Dynamical Systems and Control
Vol.05 No.04(2016), Article ID:18850,18
pages
10.12677/DSC.2016.54018
Padé Approximation and Its Application in Solving Nonlinear Systems
Youhua Qian*, Haixia Fu, Liang Shen
College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua Zhejiang

Received: Oct. 8th, 2016; accepted: Oct. 27th, 2016; published: Oct. 31st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Many problems in engineer science and natural science are often summed up in solving nonlinear systems. For many years, the rational function approximation has attracted more and more attention, which is one of the typical nonlinear approximation approaches. We mainly study one of the classical rational function approximations—Padé approximation in this paper. We take the orthogonal function system as the base function, and study some Padé approximation problems under the base function of orthogonal trigonometric function and orthogonal polynomial function respectively. Then the approximation effect is demonstrated by the concrete examples. Finally, we combine the Padé approximation with the homotopy analysis method to solve the nonlinear system, and verify its effectiveness by a three-degree-of-freedom system.
Keywords:Padé Approximation, Orthogonal Function System, Homotopy Analysis Method, Nonlinear System

帕德逼近及在求解非线性系统中的应用
钱有华*,付海霞,沈梁
浙江师范大学数理与信息工程学院,浙江 金华

收稿日期:2016年10月8日;录用日期:2016年10月27日;发布日期:2016年10月31日

摘 要
工程和自然科学中的许多问题常常可以归结为非线性系统的求解。多年来,作为非线性逼近的典型之一的有理函数逼近愈来愈引起人们的关注。本文主要研究了帕德逼近这一经典的有理函数逼近。我们以正交函数系作为基函数,分别研究了正交三角函数系和正交多项式函数系下的帕德逼近问题,并通过具体的例子展示了其逼近效果。最后,我们将帕德逼近与同伦分析方法结合来求解非线性系统,并通过一个三自由度系统验证了它的有效性。
关键词 :帕德逼近,正交函数系,同伦分析方法,非线性系统

1. 引言
在自然科学和工程技术的实际计算中,用函数的泰勒展开的部分和作为该函数的近似是一种最基本的方法。有理函数因为其自身的特点,使得我们在它的极点附近得到的近似的效果比较好。此外,逼近公式计算的应用,因为不需要考虑自变量的高次幂,使得有理函数分式形式的逼近显得比较简单有效。此外,因为应用有理函数逼近求解时需要联立求解的高次方程的次数比应用多项式逼近求解时更低,所以有理分式逼近在求解已知函数的极点和零点时有着很大的方便性 [1] [2] 。此外,在逼近过程中应用公式进行计算时,由于无须计算自变量的高次幂,有理分式逼近表现出了有效的简化性。帕德逼近则是一种特定类型的有理函数逼近,它是泰勒多项式逼近的自然引申。也就是说,要寻找一个分子和分母的数目有限的有理函数,使得它的幂级数展开式的各项系数和给定的幂级数所对应的系数尽可能多的相同 [3] 。早在19世纪,弗罗贝尼乌斯、雅可比、帕德和其他数学家就对这种逼近进行了深入的研究,并且开发和建立了一系列重要和基本的结果,这为其今后的发展奠定了坚实的基础,后来我们称之为帕德逼近。自上世纪七十年代以来,帕德逼近的理论、方法及其应用得到了迅速发展,越来越多的科学家已经重视并对其开展了大量的研究。事实证明,帕德逼近与数学中的几个分支有着非常紧密的联系,比如逼近理论、微分方程 [4] [5] 、解析函数论等。它在量子场论 [6] 、数值分析、临界现象和控制论等其他自然科学领域的应用已经取得了显著的成效。
2. Padé逼近方法介绍
定义1 [7] [8] 经典的Padé逼近方法定义如下:
设 是由下述形式幂级数定义的函数
是由下述形式幂级数定义的函数
 (1)
(1)
如果存在两个无公共因子且次数不超过 、
、 的多项式
的多项式 、
、 ,它们的系数由下列方程所确定 [9] :
,它们的系数由下列方程所确定 [9] :
 (2)
(2)
并且假定有标准化条件 ,则称有理因式
,则称有理因式 为
为 的
的 阶Padé逼近,并记为:
阶Padé逼近,并记为: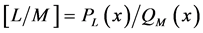 ,其中
,其中
 (3)
(3)
用 乘以(2)式并比较方程两端系数,可得关于
乘以(2)式并比较方程两端系数,可得关于 ;
; 的线性方程组(假设
的线性方程组(假设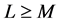 ):
):
 (4)
(4)
 (5)
(5)
利用行列式的变换可直接求得:
 (6)
(6)
3. 正交基函数下Padé逼近
3.1. 正交基函数下Padé逼近的概念
定义2设 为
为 上的连续函数,若
上的连续函数,若
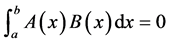 (7)
(7)
则称 与
与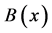 在
在 上正交。
上正交。
若函数 满足
满足
 (8)
(8)
称 在
在 上是标准化的。
上是标准化的。
我们自然考虑函数集合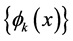 ,
, ,且具有下面性质:
,且具有下面性质:
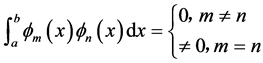 (9)
(9)
可以看出,这个集合中每两个元素都是正交的,
我们称这样的函数集合为正交函数系。
若
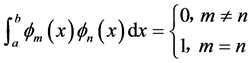
称该函数系为标准正交系。一般限制正交系中的第一个函数恒等于1。
设 为一组标准正交基函数系,则
为一组标准正交基函数系,则 。
。
定义3称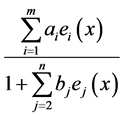 为
为 的
的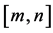 阶帕德近似,若
阶帕德近似,若
 ,
,
其中 。当
。当 时,
时, 的
的 阶帕德近似为
阶帕德近似为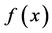 取前
取前 项。
项。
解的存在性和唯一性是判断帕德逼近在同一组基的作用下是否唯一的重要理论依据, [10] 给出了有理样条帕德逼近解的存在性和唯一性,及其相关性质,为后面的研究打下了基础。
下面考虑 的
的 阶帕德近似解的存在唯一性:
阶帕德近似解的存在唯一性:

(1) 当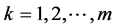 时,
时,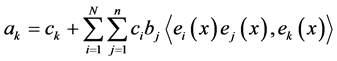 。求出
。求出 的值,自然就知道
的值,自然就知道 的值;
的值;
(2) 当 时,
时, ,
,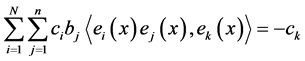 ,即
,即
 (10)
(10)
方程组(10)的系数矩阵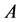 和增广矩阵
和增广矩阵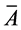 分别为
分别为
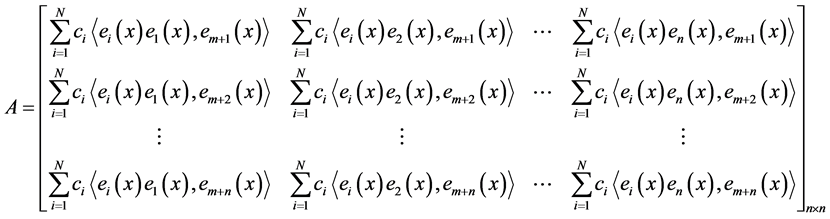

所以,当 时,方程组(10)存在唯一解,即
时,方程组(10)存在唯一解,即 的值唯一。
的值唯一。
3.2. 正交三角函数系下的Padé逼近
考虑在区间 上的三角函数系
上的三角函数系 ,通过简单计算,有如下结论:
,通过简单计算,有如下结论:
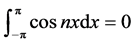
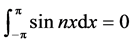

 (11)
(11)




三角函数系 ,在内积运算
,在内积运算

下构成一组正交函数系。
例1求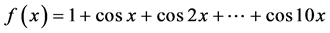 的
的 阶帕德近似。
阶帕德近似。
解:选取三角函数系 作为正交基函数,考虑
作为正交基函数,考虑

的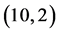 阶帕德近似。
阶帕德近似。
设 的
的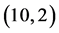 阶帕德近似为
阶帕德近似为 ,则
,则
 (12)
(12)
解得:

故 的
的 阶帕德近似为:
阶帕德近似为:
 (13)
(13)
同理可求得 的
的 阶帕德近似为:
阶帕德近似为:
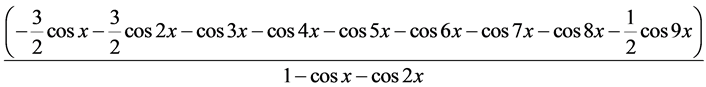 (14)
(14)
 的
的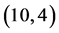 阶帕德近似为:
阶帕德近似为:
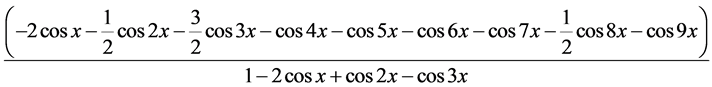 (15)
(15)
 的
的 阶帕德近似为:
阶帕德近似为:
 (16)
(16)
 的
的 阶帕德近似为:
阶帕德近似为:
 (17)
(17)
 的
的 阶帕德近似为:
阶帕德近似为:
 (18)
(18)
由上述 的帕德近似解的存在唯一性条件,我们可以知道:
的帕德近似解的存在唯一性条件,我们可以知道: ,
, ,
,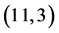 ,
, 阶帕德近似不止一个,即它们不存在唯一解。
阶帕德近似不止一个,即它们不存在唯一解。
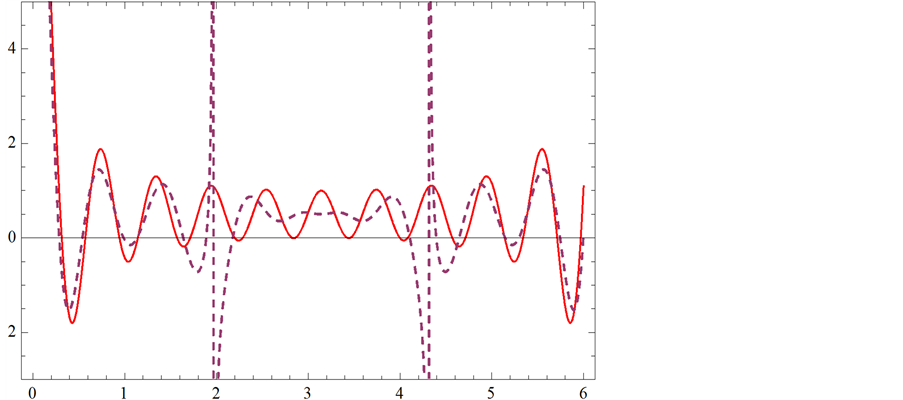
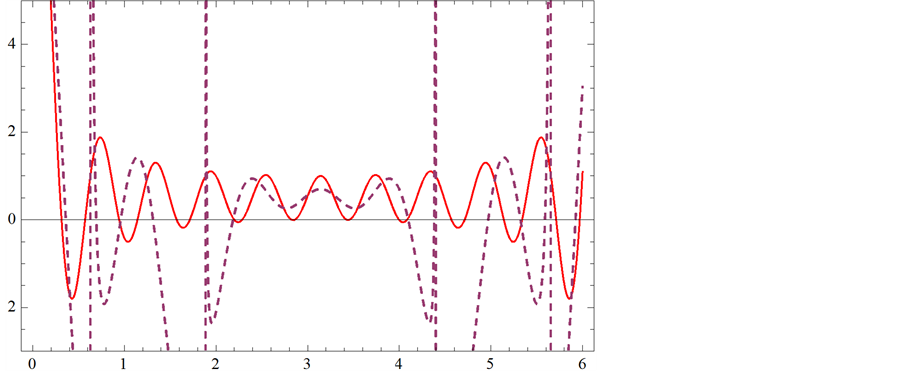
我们可以得到:图1中, 帕德近似逼近
帕德近似逼近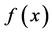 的效果是最好的,其次是图2,图3,图4,但图5,图6逼近效果最差。
的效果是最好的,其次是图2,图3,图4,但图5,图6逼近效果最差。
3.3. 正交多项式函数系下的Padé逼近
定义4 [11] 若 在区间
在区间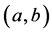 上可积,且
上可积,且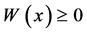 ,则
,则 可作为权函数。对于一个多项式的序列
可作为权函数。对于一个多项式的序列 和权函数
和权函数 ,定义内积:
,定义内积:
若

则这些多项式称为正交多项式。
若 除了正交之外,还有
除了正交之外,还有 ,则称
,则称 为标准正交多项式。
为标准正交多项式。
例2若权函数为1,区间为 ,
, ,对应的正交多项式序列有:
,对应的正交多项式序列有:
 紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
Figure 1. (11,3) order Padé approximation compared with f(x)
图1. (11,3)阶帕德逼近与f(x)的比较
 紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
Figure 2. (11,4) order Padé approximation compared with f(x)
图2. (11,4)阶帕德逼近与f(x)的比较
 (19)
(19)
 紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
Figure 3. (11,2) order Padé approximation compared with f(x)
图3. (11,2)阶帕德逼近与f(x)的比较
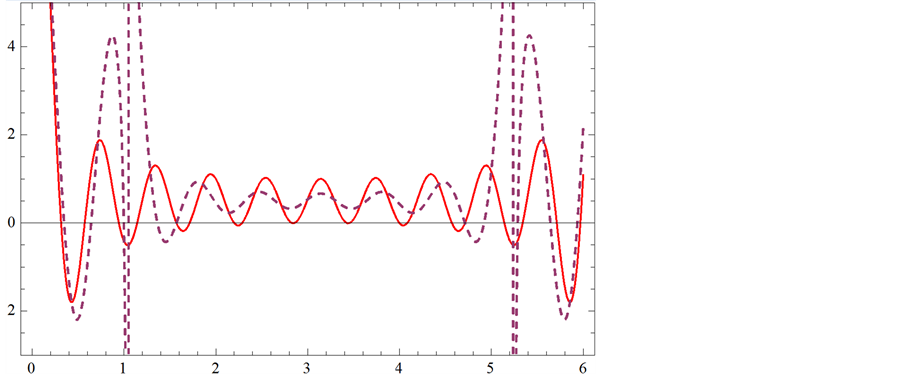 紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
Figure 4. (10,2) order Padé approximation compared with f(x)
图4. (10,2)阶帕德逼近与f(x)的比较
它们称为勒让德多项式。
对于任意向量空间的基,Gram-Schmidt正交化可以求出一个正交基。对于多项式空间的基,正交化的结果便是勒让德多项式。
例3设 ,利用勒让德多项式作为基函数,求
,利用勒让德多项式作为基函数,求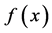 的
的 阶帕德近似。
阶帕德近似。
当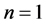 时,求
时,求 的
的 阶帕德近似,求得在勒让德多项式作为基函数时,
阶帕德近似,求得在勒让德多项式作为基函数时, 的
的 阶帕德近似为:
阶帕德近似为:
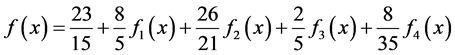 (20)
(20)
根据正交多项式下Padé逼近的定义,求得 的
的 阶帕德近似为:
阶帕德近似为:
 (21)
(21)
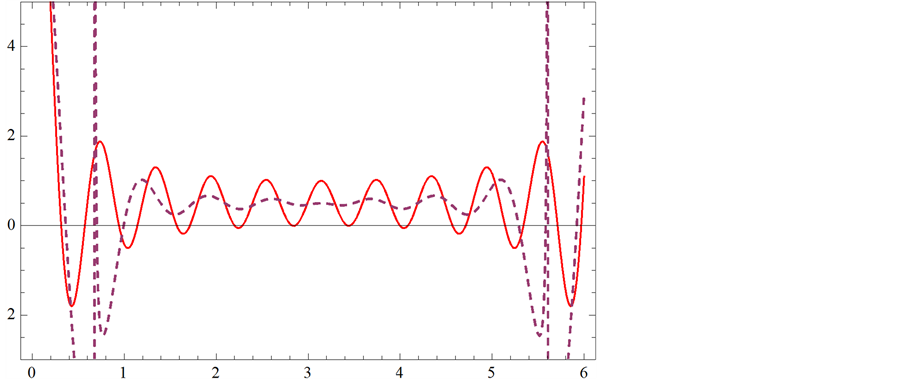 紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
Figure 5. (10,3) order Padé approximation compared with f(x)
图5. (10,3)阶帕德逼近与f(x)的比较
 紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
Figure 6. (10,4) order Padé approximation compared with f(x)
图6. (10,4)阶帕德逼近与f(x)的比较
 的
的 阶帕德近似为:
阶帕德近似为:
 (22)
(22)
 的
的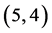 阶帕德近似为:
阶帕德近似为:
 (23)
(23)
 的
的 阶帕德近似为:
阶帕德近似为:
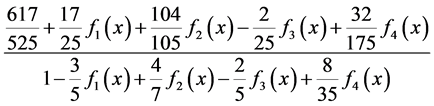 (24)
(24)
图7,图8的逼近效果最理想。图9的整体趋势吻合,但 的帕德近似与
的帕德近似与 的解吻合效果并不好。图10在
的解吻合效果并不好。图10在 上
上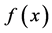 的帕德近似与
的帕德近似与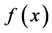 的解是吻合的,当
的解是吻合的,当 时,误差也随之变大。图11在
时,误差也随之变大。图11在 这段逼近效果最佳,但当
这段逼近效果最佳,但当 时,
时, 的帕德近似与
的帕德近似与 整体趋势不吻合。
整体趋势不吻合。
4. 帕德逼近在非线性系统求解中的应用
实际生活中非线性问题是经常出现的。由于非线性系统的复杂性,求解时直接法几乎是不能使用的。
 紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
Figure 7. (5,2) order Padé approximation compared with f(x)
图7. (5,2)阶帕德逼近与f(x)的比较
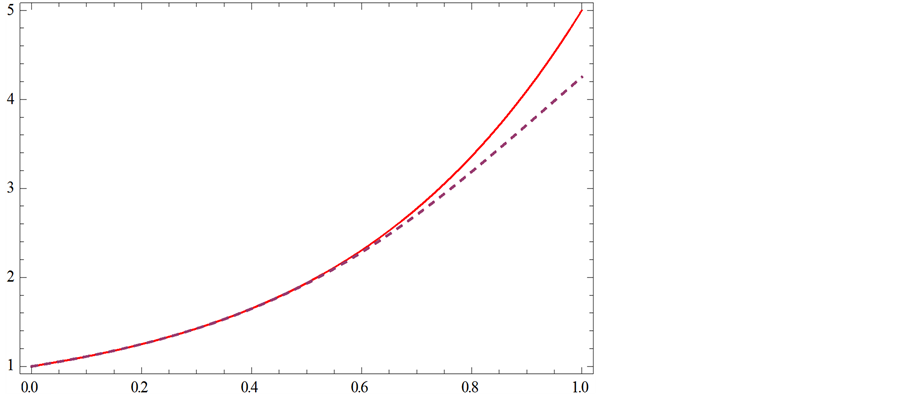 紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
Figure 8. (5,4) order Padé approximation compared with f(x)
图8. (5,4)阶帕德逼近与f(x)的比较
 紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
Figure 9. (5,1) order Padé approximation compared with f(x)
图9. (5,1)阶帕德逼近与f(x)的比较
 紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
Figure 10. (5,3) order Padé approximation compared with f(x)
图10. (5,3)阶帕德逼近与f(x)的比较
本文中我们引用同伦分析法来求解非线性系统,因为同伦分析法的优点是克服了摄动方法依赖于小参数的局限性,而且它在逻辑上包含了其他非摄动方法,更具有一般性。但是这种方法也有无法回避的缺点,因此我们很有必要发展一种能解决多自由度线性系统的解析近似方法。鉴于帕德逼近的高度精确性的优势 [12] ,也有很多学者在研究如何将其应用于求解中,并且取得了一些较大的进展。如对最低阶的函数求解其帕德逼近,展开后得到一种新的非线性方程求根的迭代算法。
受帕德逼近的启发,我们想到能否将帕德逼近应用于非线性系统中的求解呢?将求解非线性系统的一种方法——同伦分析法与帕德逼近相结合再进行求解。
4.1. 同伦分析方法
考虑多自由度非线性系统的一般表达式:
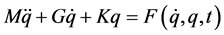 (25)
(25)
 紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
紫虚线代表f(x)帕德逼近曲线;红实线代表f(x)曲线
Figure 11. (5,5) order Padé approximation compared with f(x)
图11. (5,5)阶帕德逼近与f(x)的比较
其中,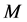 是质量系数矩阵、
是质量系数矩阵、 是
是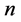 维未知向量、
维未知向量、 是线性刚度系数矩阵、
是线性刚度系数矩阵、 是阻尼系数矩阵,它们都是
是阻尼系数矩阵,它们都是 阶仿真,
阶仿真,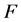 是关于
是关于 的向量值函数。系统的非线性体现在
的向量值函数。系统的非线性体现在 上。特别地,若
上。特别地,若 ,则该系统为线性系统。
,则该系统为线性系统。
下面我们用同伦分析的思想来求解系统(24),先定义一个非线性算子:
 (26)
(26)
这里 是未知向量函数,
是未知向量函数, 和
和 分别代表时间和空间自变量,设
分别代表时间和空间自变量,设
 (27)
(27)
且
 (28)
(28)
 (29)
(29)
设 为系统(24)的精确解
为系统(24)的精确解 的初始猜测解,
的初始猜测解,
 ,
, 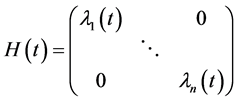
其中 ,
, 为非零实数。一般情况下,我们取
为非零实数。一般情况下,我们取 ,
, ,这样
,这样 可以看成是一个非零常数。
可以看成是一个非零常数。
引进辅助线性算子 ,满足:若
,满足:若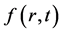 为
为 维零向量,则有
维零向量,则有 。设
。设 为嵌入变量,构造如下同伦:
为嵌入变量,构造如下同伦:
 (30)
(30)
令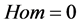 ,得到零阶形变方程:
,得到零阶形变方程:
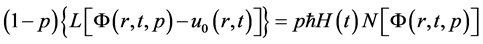 (31)
(31)
当 时,由
时,由 的性质知
的性质知 为(30)的解;当
为(30)的解;当 时,(25)的精确解
时,(25)的精确解 为(31)的解。因此,根据微分方程中解对初值的连续依赖性,当嵌入变量
为(31)的解。因此,根据微分方程中解对初值的连续依赖性,当嵌入变量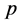 从0增大到1时,
从0增大到1时,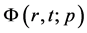 从初始猜测解
从初始猜测解 连续变化到原始方程的精确解
连续变化到原始方程的精确解 。这种连续变化在同伦理论中称为形变。
。这种连续变化在同伦理论中称为形变。
现定义 阶形变向量导数
阶形变向量导数


利用向量值函数的泰勒展开定理, 可以展开成关于
可以展开成关于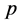 的幂级数:
的幂级数:
 (32)
(32)
于是
 (33)
(33)
需要注意的是,我们拥有很大的自由选取辅助线性算子 、辅助矩阵参数
、辅助矩阵参数 、初始猜测解
、初始猜测解 。假设它们选取合适,那么有:
。假设它们选取合适,那么有:
对所有的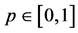 ,零阶形变方程(31)的解
,零阶形变方程(31)的解 都存在;
都存在;
对 ,形变向量导数
,形变向量导数 都存在;
都存在;
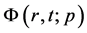 的幂级数(33)在
的幂级数(33)在 时收敛。
时收敛。
在上述假设下,我们求得系统(25)的级数解为
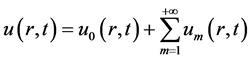 (34)
(34)
为方便起见,以向量函数为分量构成的向量定义如下:
 (35)
(35)
将零阶形变方程(31)对嵌入变量 求导
求导 次,然后除以
次,然后除以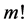 ,最后令
,最后令 ,得到
,得到 阶形变方程
阶形变方程
 (36)
(36)
其中
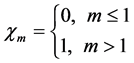
且
 (37)
(37)
于是
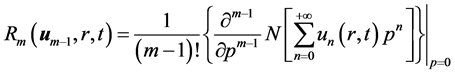 (38)
(38)
该高阶形变方程只依赖于向量函数构成的矢量 ,所以通过依次求解线性高阶形变方程(37)可一次得到
,所以通过依次求解线性高阶形变方程(37)可一次得到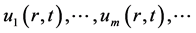 ,易知
,易知 的
的 阶近似解为
阶近似解为
 (39)
(39)
利用maple,mathematica等数学软件可以求出满足一定精度条件的近似解。
4.2. 同伦帕德逼近方法
帕德逼近可以应用到同伦分析方法中去,我们把这种改进的方法称为同伦–帕德逼近。从级数(33)出发,我们对嵌入变量 使用帕德近似,得到
使用帕德近似,得到 阶同伦–帕德近似解为
阶同伦–帕德近似解为
 (40)
(40)
很多时候, 阶同伦–帕德近似比
阶同伦–帕德近似比 阶同伦分析解更加精确。
阶同伦分析解更加精确。
由于级数(34)是收敛的,因此如果我们选取的基函数是 ,那么就可以按照变量
,那么就可以按照变量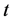 的幂对级数(39)进行重排,设
的幂对级数(39)进行重排,设
 (41)
(41)
则改进的 阶同伦–帕德逼近就可以写成如下形式
阶同伦–帕德逼近就可以写成如下形式
 (42)
(42)
4.3. 具体例子
下面看一个非线性系统的例子:
 (43)
(43)
满足初始条件
 ,
,  ,
,  ,
,  ,
,  ,
, 
该系统满足初始条件的精确解为
 ,
,  ,
,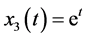 (44)
(44)
初始猜测解:
 ,
,  ,
, (45)
(45)
辅助线性算子:
 (46)
(46)
非线性算子:
 (47)
(47)
零阶形变方程:
 (48)
(48)
 阶形变方程:
阶形变方程:
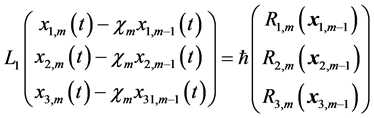 (49)
(49)
根据初始条件和初始猜测解有:
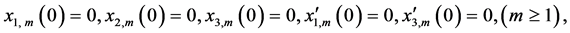
且
 (50)
(50)
仿照(25)的做法,我们再用mathematica编程,对 解
解 阶形变方程(48):
阶形变方程(48):
 (51)
(51)
再令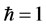 ,算得
,算得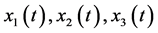 的6阶解析近似分别为
的6阶解析近似分别为
 (52)
(52)
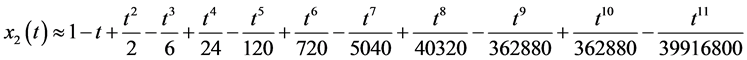 (53)
(53)
 (54)
(54)
在 范围内,我们画出
范围内,我们画出 的10阶解析近似的图像。
的10阶解析近似的图像。
如图12所示,我们可以看出:当 时,用我们的同伦分析方法求得的非线性系统(43)的近似解与其精确解的确非常接近;但当
时,用我们的同伦分析方法求得的非线性系统(43)的近似解与其精确解的确非常接近;但当 在更大的范围内取值时,就会产生较大的误差。因此,我们考虑用同伦Padé逼近方法来改进,过程如上诉方法分析,求得[5,5]阶同伦–帕德近似解,其图像如下所示。
在更大的范围内取值时,就会产生较大的误差。因此,我们考虑用同伦Padé逼近方法来改进,过程如上诉方法分析,求得[5,5]阶同伦–帕德近似解,其图像如下所示。
如图13所示,我们可以看出:同伦Padé逼近求解的近似解和精确解的吻合范围差不多,并没有扩大,即帕德逼近对于用同伦方法求解非线性方程时能加速解的收敛性。
由上述分析结果显示,即使时间历程 处于一个较大的范围,结合了帕德逼近和同伦分析方法的解析解仍然与数值积分解吻合得很好。也就是说,运用同伦–帕德逼近的技巧加速解的收敛性。在求非线性解析解的时候,帕德逼近作为一种特殊的有理函数逼近,能够有效的将结果的正确范围扩大,从而有利
处于一个较大的范围,结合了帕德逼近和同伦分析方法的解析解仍然与数值积分解吻合得很好。也就是说,运用同伦–帕德逼近的技巧加速解的收敛性。在求非线性解析解的时候,帕德逼近作为一种特殊的有理函数逼近,能够有效的将结果的正确范围扩大,从而有利

 紫虚线代表近似解,红实线代表精确解
紫虚线代表近似解,红实线代表精确解
Figure 12. The curves of x1(t), x2(t), x3(t) are obtained by the homotopy analysis method for nonlinear systems
图12. 非线性系统同伦分析方法所得x1(t),x2(t),x3(t)

 紫虚线代表近似解,红实线代表精确解
紫虚线代表近似解,红实线代表精确解
Figure 13. The curves of x1(t), x2(t), x3(t) are obtained by homotopy padé approximation method
图13. 同伦Padé逼近方法所得x1(t),x2(t),x3(t)
于我们对于数学问题结果的计算和预测 [13] [14] [15] [16] 。因此,研究帕德逼近及在非线性系统中的应用是十分必要的。
基金项目
感谢国家自然科学基金项目(11572288)的资助!
文章引用
钱有华,付海霞,沈 梁. 帕德逼近及在求解非线性系统中的应用
Padé Approximation and Its Application in Solving Nonlinear Systems[J]. 动力系统与控制, 2016, 05(04): 161-178. http://dx.doi.org/10.12677/DSC.2016.54018
参考文献 (References)
- 1. 徐献瑜. Padé逼近概论[M]. 上海: 上海科学技术出版社, 1990.
- 2. Baker, G.A. (1975) Essentials of Padéapproximants. Academic Press, New York.
- 3. Baker, G.A. and Graves-Morris, P. (1981) Padé Approximants. Part 1: Basic theory. Encyclopedia of Mathematics and Its Applications, Addison-Wesley, Reading.
- 4. Vakakis, A.F. and Azeez, M.F.A. (1998) ANALYTIC approximation of the Homoclinic Orbits of the Lorenz System at σ = 10, b = 8/3 and ρ = 13.926. Nonlinear Dynamics, 15, 245-257. http://dx.doi.org/10.1023/A:1008202529152
- 5. Mikhlin, Y.V. (2000) Analytical Construction of Homoclinic Orbits of Two- and Three-Dimensional Dynamical Systems. Journal of Sound and Vibration, 230, 971-983. http://dx.doi.org/10.1006/jsvi.1999.2669
- 6. Wheeler, J.C. and Gordon, R. (1970) The Padé Approximant in Theoretical Physics. Academic, New York.
- 7. 王仁宏. 数值有理逼近[M]. 上海: 上海科学技术出版杜, 1980.
- 8. 王仁宏. 数值逼近[M]. 北京: 高等教育出版社, 1999.
- 9. Prevost, M. (2000) Diophantine Approximations Using Padé Approximations. Journal of Computational and Applied Mathematics, 122, 231-50. http://dx.doi.org/10.1016/S0377-0427(00)00365-4
- 10. 朱功勤. 多元有理逼近方法[M]. 北京: 中国科学技术出版社, 1996.
- 11. Gautschi, W. (2001) The Use of Rational Functions in Numerical Quadrature. Journal of Computational and Applied Mathematics, 133, 111-126. http://dx.doi.org/10.1016/S0377-0427(00)00637-3
- 12. Oscar Cata. (2010) Padé Approximants and the Prediction of Non-Perturbative Parameters in Particle Physics. Applied Numerical Mathematics, 60, 1273-1285. http://dx.doi.org/10.1016/j.apnum.2010.08.011
- 13. 胡沁春, 黄立宏, 何怡刚, 李宏民. Morlet小波变换的开关电流模拟实现[J]. 湖南大学学报(自然科学版), 2009, 36(2): 58-61.
- 14. 王元庆, 洪伟. 广义传输线方程结合Padé逼近用于信号完整性分析[J]. 微波学报, 2008, 24(1): 19-22.
- 15. 辛焕海, 屠竞哲, 谢俊, 甘德强. 基于LMI的小时滞饱和系统稳定域估计方法[J]. 控制理论与应用, 2009, 26(9): 970-976.
- 16. 王福永. 基于Padé逼近的纯滞后系统内模控制器的设计[J]. 苏州大学学报(工科版), 2004, 24(4): 26-29.