Dynamical Systems and Control
Vol.06 No.03(2017), Article ID:21301,8
pages
10.12677/DSC.2017.63015
Behavior Control for Boiti-Leon-Pempinelli Nonlinear System Based on Confined Riccati Equation
Qing Liu
Institute of Optics and Electronics, School of Engineering, Lishui University, Lishui Zhejiang

Received: Jun. 16th, 2017; accepted: Jul. 7th, 2017; published: Jul. 10th, 2017

ABSTRACT
A series of traveling waves of q-deformation hyperbolic function, q-deformation trigonometric function, hyperbolic function and trigonometric function for BLP nonlinear system are investigated. The relationship is found between various dynamical behavior of BLP system and multiple parameters based on confined Riccati equation. Predicting variation of the behavior of nonlinear system using variation of these parameters is proposed. Idea to control dynamical behavior of nonlinear system by means of changing parameters is given.
Keywords:Behavior Control, Nonlinear System, Riccati Equation
基于Riccati方程约束的Boiti-Leon-Pempinelli 非线性系统行为的控制
留庆
丽水学院工学院光电研究所,浙江 丽水
收稿日期:2017年6月16日;录用日期:2017年7月7日;发布日期:2017年7月10日

摘 要
Boiti-Leon-Pempinelli (BLP)非线性系统的许多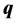 形变双曲函数、
形变双曲函数、 形变三角函数、双曲函数和三角函数形式行波解被研究。研究表明在Riccati方程条件下,BLP系统不同的动力行为与被约束Riccati方程的多个参量之间存在着联系。为此,提出借助这些参量来预报非线性系统行为变化规律,和利用改变参量的方法实现对非线性系统的动力学行为控制的思想。
形变三角函数、双曲函数和三角函数形式行波解被研究。研究表明在Riccati方程条件下,BLP系统不同的动力行为与被约束Riccati方程的多个参量之间存在着联系。为此,提出借助这些参量来预报非线性系统行为变化规律,和利用改变参量的方法实现对非线性系统的动力学行为控制的思想。
关键词 :行为控制,非线性系统,Riccati方程

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在物理学、光学、力学、工程技术等领域,非线性系统被广泛用于描述各种自然现象和动力学规律,对非线性系统解析解的研究成为人们研究非线性系统动力学行为的一种重要手段和方法。许多求解非线性偏微分方程解析解的方法被不断地提出和发展,如形变映射法 [1] 、Cole-Hopf变换法 [2] 、拓展tanh函数法 [3] 、进一步拓展tanh函数法 [4] 、Riccati方程映射法 [5] 、有理函数方法 [6] 、Riccati方程展开法 [7] 、多 Riccati方程有理数展开法 [8] 、多Riccati方程有理函数指数法 [9] ,等等。
(2 + 1)维Boiti-Leon-Pempinelli (BLP)非线性系统
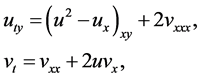 (1)
(1)
被广泛地用于研究原子物理、分子物理、粒子物理领域的一些实际问题。许多研究者用多种方法获得了BLP非线性系统不同类型丰富的解析解 [10] [11] [12] [13] [14] ,这些形式完全不相同的解析解之间是否存在相互联系?目前还没有这方面相关的进展。
这篇论文研究了在Riccati方程约束条件下,BLP非线性系统的一些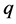 形变双曲函数、
形变双曲函数、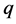 形变三角函数、双曲函数或三角函数形式的行波解。结果发现这些不同形式的行波解之间存在着相互联系,并非是独立的。通过改变Riccati方程的参量,能使这些
形变三角函数、双曲函数或三角函数形式的行波解。结果发现这些不同形式的行波解之间存在着相互联系,并非是独立的。通过改变Riccati方程的参量,能使这些 形变双曲函数、
形变双曲函数、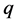 形变三角函数、双曲函数或三角函数形式行波解之间相互转化。基于这些结果,本论文提出利用参量的变化规律来预测BLP非线性系统的动力学行为的变化规律,借助改变参量实现对非线性系统动力学行为控制的思想。
形变三角函数、双曲函数或三角函数形式行波解之间相互转化。基于这些结果,本论文提出利用参量的变化规律来预测BLP非线性系统的动力学行为的变化规律,借助改变参量实现对非线性系统动力学行为控制的思想。
2. 带多个任意参量的BLP非线性系统的有理指数解
为了揭示出对受Riccati方程约束的BLP非线性系统的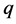 形变双曲函数、
形变双曲函数、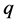 形变三角函数、双曲函数或三角函数形式行波解之间内在的联系。首先必须设法能将这些不同形式的行波解统一起来。其解决方案是寻找(2 + 1)维BLP系统带多个任意参量统一的有理指数解。其方法如下:
形变三角函数、双曲函数或三角函数形式行波解之间内在的联系。首先必须设法能将这些不同形式的行波解统一起来。其解决方案是寻找(2 + 1)维BLP系统带多个任意参量统一的有理指数解。其方法如下:
对BLP系统作以下变换
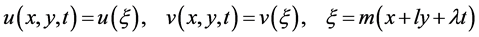 (2)
(2)
即把方程(2)代入方程(1)中,简化后可得到:
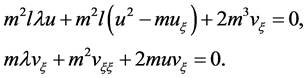 (3)
(3)
设方程(3)有下列拟解:
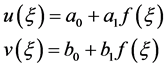 (4)
(4)
其中 是待定常数,函数
是待定常数,函数 满足Riccati方程:
满足Riccati方程:
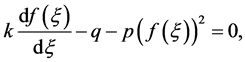 (5)
(5)
其中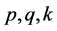 都是常数。方程(5)有下列带多任意参量的有理指数解 [6] :
都是常数。方程(5)有下列带多任意参量的有理指数解 [6] :
 (6)
(6)
其中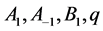 为任意常量,
为任意常量,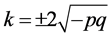 。
。
把方程(4)~(5)代入方程(3),然后令结果方程中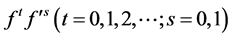 的所有系数为零,得到一组的关于
的所有系数为零,得到一组的关于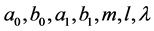 的代数方程组。求解这组代数方程,可得:
的代数方程组。求解这组代数方程,可得:
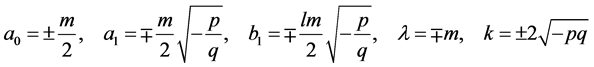 (7)
(7)
其中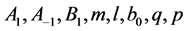 是任意常量。
是任意常量。
把方程(7)连同方程(6)代入方程(4),化简得到方程(1)有下列有理指数函数解:
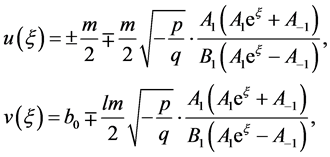 (8)
(8)
其中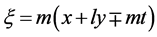 ,而
,而 是任意常量,
是任意常量, 。需要指出的是,若
。需要指出的是,若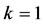 ,方程(8)是方程(1)的解;若
,方程(8)是方程(1)的解;若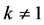 时,需要对方程(8)等式右边所有的
时,需要对方程(8)等式右边所有的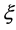 ,作
,作 变换后才是方程(1)的解。
变换后才是方程(1)的解。
3. BLP非线性系统不同的动力学行为及控制方法
方程(8)是BLP非线性系统带多个任意参量的有理指数函数解,对这些任意参量赋予某些确定的值和对方程(8)中的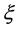 作
作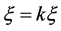 变换后,能够写出BLP系统已知的
变换后,能够写出BLP系统已知的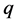 形变双曲函数、
形变双曲函数、 形变三角函数、双曲函数、三角函数形式的行波解,获得BLP系统丰富的动力学行为。
形变三角函数、双曲函数、三角函数形式的行波解,获得BLP系统丰富的动力学行为。
(1) 设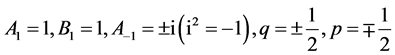 ,那么
,那么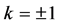 。取
。取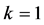 ,方程(8)变成
,方程(8)变成
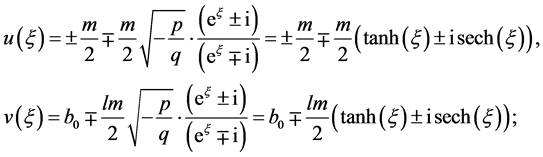 (9)
(9)
(2) 设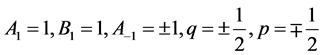 ,那么
,那么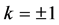 。取
。取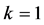 ,方程(8)变成
,方程(8)变成
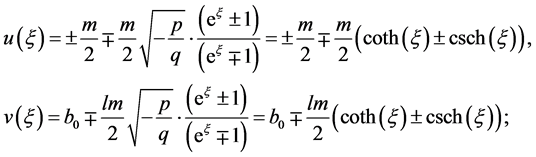 (10)
(10)
(3) 设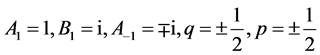 ,那么
,那么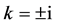 。取
。取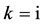 ,做
,做 变换,方程(8)变成
变换,方程(8)变成
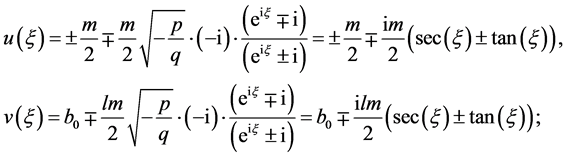 (11)
(11)
(4) 设 ,那么
,那么 。取
。取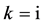 ,做
,做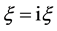 变换,方程(8)变成
变换,方程(8)变成
 (12)
(12)
(5) 设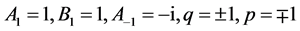 ,那么
,那么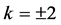 。取
。取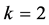 ,做
,做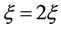 变换,方程(8)变成
变换,方程(8)变成
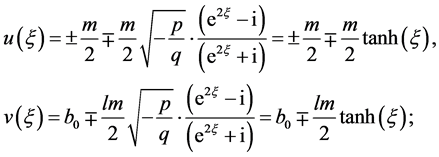 (13)
(13)
(6) 设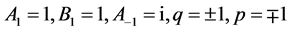 ,那么
,那么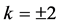 。取
。取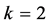 ,做
,做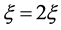 变换,方程(8)变成
变换,方程(8)变成
 (14)
(14)
(7) 设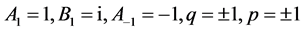 ,那么
,那么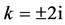 。取
。取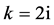 ,做
,做 变换,方程(8)变成
变换,方程(8)变成
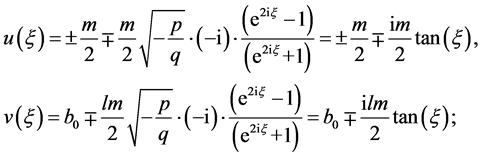 (15)
(15)
(8) 设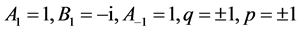 ,那么
,那么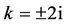 。取
。取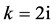 ,做
,做 变换,方程(8)变成
变换,方程(8)变成
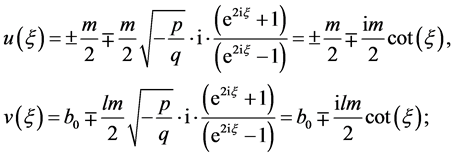 (16)
(16)
(9) 设 ,那么
,那么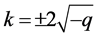 ,取
,取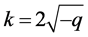 ,做
,做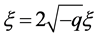 变换方程(8)变成
变换方程(8)变成
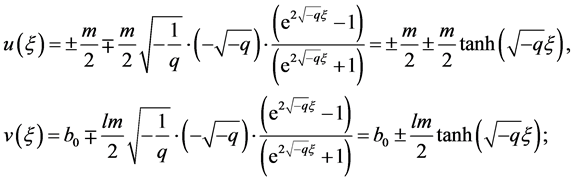 (17)
(17)
(10) 设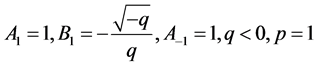 ,那么
,那么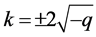 ,取
,取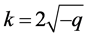 ,做
,做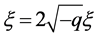 变换方程(8)变成
变换方程(8)变成
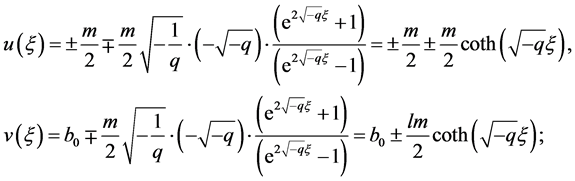 (18)
(18)
(11) 设 ,那么
,那么 ,取
,取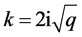 ,做
,做 变换方程(8)变成
变换方程(8)变成
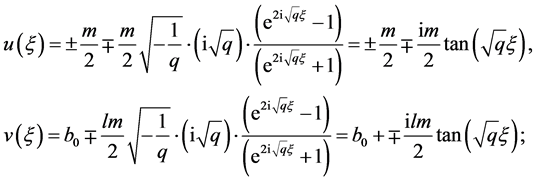 (19)
(19)
(12) 设 ,那么
,那么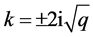 ,取
,取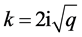 ,做
,做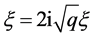 变换方程(8)变成
变换方程(8)变成
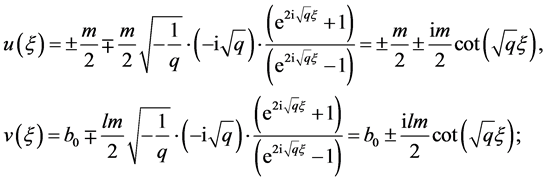 (20)
(20)
(13) 设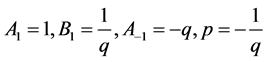 ,那么
,那么 ,取
,取 ,做
,做 变换方程(8)变成
变换方程(8)变成
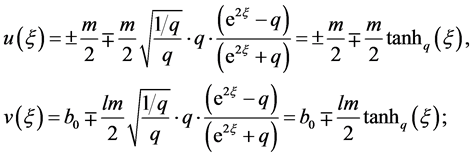 (21)
(21)
(14) 设 ,那么
,那么 ,取
,取 ,做
,做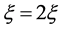 变换方程(8)变成
变换方程(8)变成
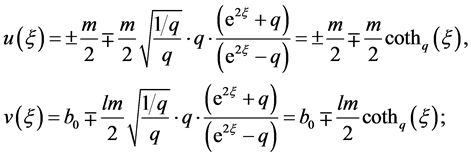 (22)
(22)
(15) 设 ,那么
,那么 ,取
,取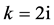 ,做
,做 变换方程(8)变成
变换方程(8)变成
 (23)
(23)
(16) 设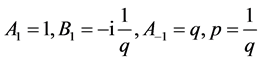 ,那么
,那么 ,取
,取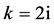 ,做
,做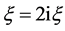 变换方程(8)变成
变换方程(8)变成
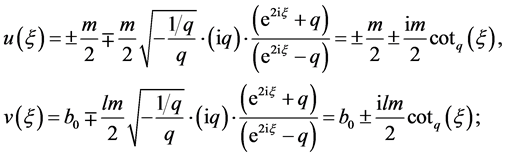 (24)
(24)
其中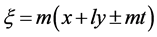 ,而
,而 是任意常量。
是任意常量。
方程(9)~(24)仅是参量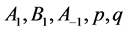 取某些特定值,从方程(8)获得具有
取某些特定值,从方程(8)获得具有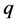 形变双曲函数、
形变双曲函数、 形变三角函数、双曲函数或三角函数形式的BLP非线性系统的行波解。显然它们都是方程(8)的特解,这些解尽管形式不相同,好像彼此不相干,实际上它们是通过方程(8)中的参量
形变三角函数、双曲函数或三角函数形式的BLP非线性系统的行波解。显然它们都是方程(8)的特解,这些解尽管形式不相同,好像彼此不相干,实际上它们是通过方程(8)中的参量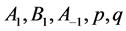 联系在一起。由于参量
联系在一起。由于参量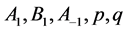 是任意常量,从理论上来说方程(8)能得到无限多的BLP非线性系统的行波解,表示BLP非线性系统具有无限多不相同的动力行为。这些行为中绝大部分是无法用
是任意常量,从理论上来说方程(8)能得到无限多的BLP非线性系统的行波解,表示BLP非线性系统具有无限多不相同的动力行为。这些行为中绝大部分是无法用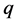 形变双曲函数、
形变双曲函数、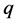 形变三角函数、双曲函数或三角函数形式表示的行波解,只能写成有理指数函数形式的行波解。由于这些BLP非线性系统的行波解,都是被参量
形变三角函数、双曲函数或三角函数形式表示的行波解,只能写成有理指数函数形式的行波解。由于这些BLP非线性系统的行波解,都是被参量 联系在一起,因此,掌握了这些参量的变化规律,我们就能预测BLP非线性系统行为的变化规律。例如:当约束方程参量满足
联系在一起,因此,掌握了这些参量的变化规律,我们就能预测BLP非线性系统行为的变化规律。例如:当约束方程参量满足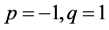 ,内部参量
,内部参量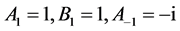 时,我们能预测BLP非线性能产生冲击波。
时,我们能预测BLP非线性能产生冲击波。
另一方面,如果想要控制BLP非线性系统动力学行为,只要控制好与之相对应的参量 值就可实现。并可通过参量
值就可实现。并可通过参量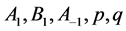 数值的变化,实现BLP非线性系统在不同行为之间的转化。例如:需要减弱或削除冲击波对BLP非线性产生的影响,可以借助方程(8),通过改变约束参量
数值的变化,实现BLP非线性系统在不同行为之间的转化。例如:需要减弱或削除冲击波对BLP非线性产生的影响,可以借助方程(8),通过改变约束参量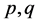 和内部参量
和内部参量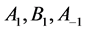 的方法,削弱冲击波的幅度,或将其转化为其它种类的行波。
的方法,削弱冲击波的幅度,或将其转化为其它种类的行波。
4. 结论
本论文构造了一个广义的Riccati方程,并获得该方程归一化的带多参量的有理解数函数解,利用这个广义的Riccati方程和这个归一化的有理解数函数解,求得了(2 + 1)维Boiti-Leon-Pempinelli非线性系统广义的有理指数函数解。借助这个解中包含的多个参量和一个简单的自变量变换方法,就能获得BLP非线性系统丰富的行波解,包括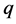 形变双曲函数、
形变双曲函数、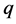 形变三角函数、双曲函数、三角函数和有理指数函数形式的行波解。一个重要的应用是,可借助BLP非线性系统解析解中包含的多个参量,来预测BLP非线性系统动力行为变化规律,以及通过控制参量变化的方法,实现对BLP非线性系统动力行为的控制。
形变三角函数、双曲函数、三角函数和有理指数函数形式的行波解。一个重要的应用是,可借助BLP非线性系统解析解中包含的多个参量,来预测BLP非线性系统动力行为变化规律,以及通过控制参量变化的方法,实现对BLP非线性系统动力行为的控制。
本论文给出了在广义的Riccati方程约束条件下BLP非线性系统带有多参量的有理解数函数解,揭示出这个解包含丰富的动力行为。但对于BLP非线性系统某个具体的动力行为,哪些参量是影响其行为的主要因素?对于BLP非线性系统不同的动力行为,这些参量对其行为影响的地位是否会发生变化?存在着什么的规律?这些问题有待于进一步研究。
致谢
本项目获得浙江省自然科学基金资助,项目号:LY13A050001。
基金项目
浙江省自然科学基金资助,项目号:LY13A050001。
文章引用
留 庆. 基于Riccati方程约束的Boiti-Leon-Pempinelli非线性系统行为的控制
Behavior Control for Boiti-Leon-Pempinelli Nonlinear System Based on Confined Riccati Equation[J]. 动力系统与控制, 2017, 06(03): 119-126. http://dx.doi.org/10.12677/DSC.2017.63015
参考文献 (References)
- 1. Lou, S.Y. and Ni, G.J. (1989) The Relations among a Special Type of Solutions in Some (D + 1)-Dimensional Nonlinear Equations. Journal of Mathematical Physics, 30, 1614-1620. https://doi.org/10.1063/1.528294
- 2. Ma, W.X. and Fuchssteiner, B. (1996) Explicit and Exact Solutions to a Kolmogorov-Petrovskii-Piskunov Equation. International Journal of Non-Linear Mechanics, 31, 329-338. https://doi.org/10.1016/0020-7462(95)00064-X
- 3. Fan, E.G. (2000) Extended Tanh-Function Method and Its Applications to Nonlinear Equations. Physics Letters A, 277, 212-218. https://doi.org/10.1016/S0375-9601(00)00725-8
- 4. Dai, C.Q. and Wang, Y.Y. (2008) Combined Wave Solutions of the (2 + 1)-Dimensional Generalized Nizhnik-Novi- kov-Veselov System. Physics Letters A, 372, 1810-1815. https://doi.org/10.1016/j.physleta.2007.05.120
- 5. Liu, Q. (2007) Some Exact Solutions for Stochastic mKdV Equation. Chaos, Solitons & Fractals, 32, 1224-1230. https://doi.org/10.1016/j.chaos.2005.11.044
- 6. Liu, Q., Shen, S.Y. and Wang, Z.H. (2013) The Rational Solutions to a Generalized Riccati Equation and Their Application. International Journal of Modern Physics B, 27, 1350013. https://doi.org/10.1142/S0217979213500136
- 7. 张文玲, 马松华, 陈晶晶. (2 + 1)维Korteweg-de Vries 方程的复合波解及局域激发[J]. 物理学报, 2014, 63(8): 58- 64.
- 8. Chen, Y. and Wang, Q. (2005) Multiple Riccati Equa-tions Rational Expansion Method and Complexiton Solutions of the Whitham-Broer-Kaup Equation. Physics Letters A, 347, 215-227. https://doi.org/10.1016/j.physleta.2005.08.015
- 9. Liu, Q., Wang, Z.H. and Jia, D.L. (2013) A Multiple Riccati Equations Rational-Exponent Method and Its Application to Whitham-Broer-Kaup Equation. International Journal of Modern Physics B, 27, 1350014. https://doi.org/10.1142/S0217979213500148
- 10. Fang, J.P., Ma, S.H., Fei, J.X., Hong, B.H. and Zheng, C.L. (2007) Localized Structures on Periodic Background Wave of (2 + 1)-Dimensional Boiti-Leon-Pempinelli System via an Object Reduction. Communications in Theoretical Physics, 48, 811-814. https://doi.org/10.1088/0253-6102/48/5/009
- 11. 马松华, 强继业, 方建平. (2 + 1)维Boiti-Leon-Pempinelli 系统的混沌行为及孤子间的相互作用[J]. 物理学报, 2007, 56(2): 620-627.
- 12. 费金喜, 应颖洁, 雷燕. (2 + 1)维Boiti-Leon-Pempinelli方程系统的对称约化和精确解[J]. 丽水学院学报, 2014, 36: 8-14.
- 13. Feng, W.G., Li, K.M., Li, Y.Z. and Lin, C. (2009) Explicit Exact Solutions for (2 + 1)-Dimensional Boiti-Leon-Pem- pinelli Equation. Communications in Nonlinear Science and Numerical Simulation, 14, 2013-2017. https://doi.org/10.1016/j.cnsns.2008.06.005
- 14. 蔡珊珊, 周钰谦, 刘倩. (2 + 1)维Boiti-Leon-Pempinelli方程的椭圆函数周期波解[J]. 四川师范大学学报(自然科学版), 2015, 38(4): 504-507.