Dynamical Systems and Control
Vol.
08
No.
04
(
2019
), Article ID:
32179
,
6
pages
10.12677/DSC.2019.84026
Bifurcation Analysis of Discrete SIS Model with Saturated Incidence and Saturated Treatment Function
Yuqing Chen, Mingxuan Liang, Qiaomei Tang, Xiaoliang Zhou
School of Mathematics and Statistics, Lingnan Normal University, Zhanjiang Guangdong

Received: Aug. 23rd, 2019; accepted: Sep. 1st, 2019; published: Sep. 17th, 2019

ABSTRACT
In this paper, we discuss the discrete SIS models with saturation incidence and saturation treatment function. We obtain the type and hyperbolicity of the disease-free equilibrium point. We also use the central manifold theorem and the bifurcation theory to obtain the conditions of Transcritical bifurcation and flip bifurcation for disease-free equilibrium point. Finally, the biological explanation of bifurcation is given.
Keywords:Discrete SIS Model, Stability, Transcritical Bifurcation, Flip Bifurcation
具有饱和发生率和饱和治疗函数的离散SIS传染病模型的分岔分析
陈雨青,梁铭轩,唐巧媚,周效良
岭南师范学院数学与统计学院,广东 湛江

收稿日期:2019年8月23日;录用日期:2019年9月1日;发布日期:2019年9月17日

摘 要
本文探讨了一类具有饱和发生率和饱和治疗函数的离散SIS模型,得到模型无病平衡点的类型及双曲性利用中心流形定理与分岔理论得到无病平衡点产生跨临界分岔和flip分岔的条件。最后给出分岔的生物学解释。
关键词 :离散SIS模型,稳定性,跨临界分岔,Flip分岔

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近几十年来,为了预防和控制传染病的传播,许多传染病模型被数学家们提出 [1] [2] [3] 。传染病模型主要分为连续模型和离散模型两大类,由于公共卫生部门收集的传染病数据都是离散数据,相比于连续模型,离散模型更容易理解和应用,且离散模型具有更加丰富的动力学行为,离散模型也可以通过连续模型离散化得到,因此,近年来离散传染病模型的研究越来越多 [4] [5] 。关于离散传染病模型的研究主要集中于模型平衡点的分岔,稳定性和持久性。研究传染病模型的分岔性质可以得到传染病模型的解受外界干扰时的性态变化和其对应模型拓扑结构的变化的影响,从而得到传染病模型相关的动力学性质,这对于传染病的防控措施与流行规律的理论研究是非常重要的。
在传染病模型中,许多因素影响着模型的动力学行为,如治疗函数、发生率等。Zhang和Liu于文献 [6] 研究了具有饱和治疗函数与饱和发生率的SIR传染病模型的倒向分岔,Wang和Ruan于文献 [7] 中研究了具有常数治疗函数与双线性发生率的SIR传染病模型的鞍结点分岔、Hopf分岔和同宿分岔。在已有研究的基础上,综合考虑当医疗条件有限且感染者数量较大时延迟治疗所产生的影响,以及在特定时间里,每个染病者接触易感者的数量有限,Zhou和Zhang在文献 [8] 中研究了如下具有饱和发生率和饱和治疗函数的连续SIS模型:
(1)
这里的S和I分别代表了t时刻的易感者和染病者数量;A代表人口的补充率;d是自然死亡率;u是疾
病致死率;v指的是感染性个体的自然恢复率;饱和发生率为
, 表示单位时间内易感者接触感染者的数量;饱和治疗函数被定义为
,r指的是治愈率;
描述的是延迟治疗所产生的影响。在文献 [8] 中,作者得到模型(1)的基本再生数
,如
,无病平衡点
是不稳定的,
表示单位时间内易感者接触感染者的数量;饱和治疗函数被定义为
,r指的是治愈率;
描述的是延迟治疗所产生的影响。在文献 [8] 中,作者得到模型(1)的基本再生数
,如
,无病平衡点
是不稳定的,
如果 ,无病平衡点 是稳定的。将模型(1)离散化并进行泰勒展开,我们得到如下的离散SIS传染病模型
(2)
和 指的是n时刻易感者和染病者的数量,假定 ,系数参数 都是正的, 非负。
本文的安排如下:在第二节讨论无病平衡点 的双曲性,在第三节,应用中心流形定理研究并得到非双曲无病平衡点产生跨临界分岔和flip分岔的条件,在第四节进行了总结。
2. 平衡点分析
模型(2)的无病平衡点为 ,其雅克比矩阵为
特征值为
定义如下符号
定理2.1 无病平衡点 有以下性质:
i) 当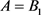 或
时,
非双曲;
或
时,
非双曲;
ii) 当 时, 全局渐近稳定;当 或 时, 是鞍点。
3. 跨临界分岔和Flip分岔
本节考虑无病平衡点 的跨临界分岔和flip分岔,选取A为分岔参数。
从第2节可知,当
时,有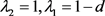 ,当
有
,定义如下符号
,当
有
,定义如下符号
定理3.1 当 时,系统(2)在无病平衡点 产生跨临界分岔。具体地讲,对A的微小扰动使得 时,无病平衡点 是双曲且稳定的;当 时无病平衡点 是双曲且不稳定的。
证明:把A看作分岔参数且把F写成 来体现对A的依赖性,易得
特征值 对应的特征向量为
(3)
利用特征向量组(3)得到如下变换
(4)
由变换(4)可以把系统(1)变为
(5)
当 时,有
,由文献 [9] 的定理2.1.4可知,无病平衡点
的稳定性与分岔可通过研究在中心流形上一参数族映射来确定,令
,在
附近的中心流形有如下形式:
时,有
,由文献 [9] 的定理2.1.4可知,无病平衡点
的稳定性与分岔可通过研究在中心流形上一参数族映射来确定,令
,在
附近的中心流形有如下形式:
假设中心流形如下
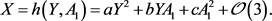
其中, 表示次数大于或等于3的项,由中心流形的不变性可得
对比 的系数解得
因此系统(1)在 附近的中心流形为
将其代入(5)中的第二个等式可得一维映射
当 时,验算如下式子成立:
(6)
根据文献 [9] 可知系统(2)在 处产生跨临界分岔,在 附近系统(2)的拓扑结构与式子(7)的拓扑结构是局部拓扑等价的。
(7)
定理3.2 当 时,系统(2)在无病平衡点 处经历flip分岔。具体地讲,当 时,系统在无病平衡点 处分岔出稳定的2周期轨;当 时,系统(2)在无病平衡点 处分岔出的2周期轨是不稳定的。
证明:令 ,在 附近的中心流形为
这里
类似定理3.1的计算可得到如下一维映射:
当
时,有
,系统(2)在无病平衡点 有
有
这里
由文献 [10] 中的定理3.5.1可知,当 时,系统(2)在无病平衡点 处经历flip分岔。
4. 分岔生物学解释
由定理3.1和定理3.2可知,在无病平衡点
处,系统(2)的局部拓扑结构对参数A非常敏感,A穿过
时,系统(2)在 的双曲性和稳定性都发生了改变;当A穿过
时,系统(2)在
经历倍周期分岔。这表明传染病的流形状态也发生相应改变。通过研究传染病模型的分岔性质,人们可以掌握传染病传播的规律,从而采取有效的措施防止传染病的传播。比如控制外来人口的数量、降低接触率、研发高效疫苗等,调整模型的系数参数,最终使模型的无病平衡点趋于稳定的状态。
的双曲性和稳定性都发生了改变;当A穿过
时,系统(2)在
经历倍周期分岔。这表明传染病的流形状态也发生相应改变。通过研究传染病模型的分岔性质,人们可以掌握传染病传播的规律,从而采取有效的措施防止传染病的传播。比如控制外来人口的数量、降低接触率、研发高效疫苗等,调整模型的系数参数,最终使模型的无病平衡点趋于稳定的状态。
基金项目
国家自然科学基金(No: 11561019);广东省攀登计划专项资金项目(No: pdjha0304/No: pdjh2019b0297);全国大学生创新创业训练计划项目(201910579725)。
文章引用
陈雨青,梁铭轩,唐巧媚,周效良. 具有饱和发生率和饱和治疗函数的离散SIS传染病模型的分岔分析
Bifurcation Analysis of Discrete SIS Model with Saturated Incidence and Saturated Treatment Function[J]. 动力系统与控制, 2019, 08(04): 242-247. https://doi.org/10.12677/DSC.2019.84026
参考文献
- 1. 马知恩, 周义仓, 吴建宏. 传染病建模与动力学[M]. 北京: 高等教育出版社, 2009.
- 2. Safi, M.A., et al. (2013) Qualitative Analysis of an Age-Structured SEIR Epidemic Model with Treatment. Applied Mathematics & Computation, 219, 10627-10642.
https://doi.org/10.1016/j.amc.2013.03.126 - 3. Wang, W. and Ruan, S. (2015) Bifurcations in an Epidemic Model with Constant Removal Rate of the Infectives. Journal of Mathematical Analysis & Applications, 291, 775-793.
https://doi.org/10.1016/j.jmaa.2003.11.043 - 4. Allen, L.J.S. (1994) Some Discrete-Time SI, SIR, and SIS Epidemic Models. Mathematical Biosciences, 124, 83-105.
https://doi.org/10.1016/0025-5564(94)90025-6 - 5. Castillo-Chavez, C. and Yakubu, A.A. (2015) Discrete-Time SIS Models with Complex Dynamics. Nonlinear Analysis, 47, 4753-4762.
https://doi.org/10.1016/S0362-546X(01)00587-9 - 6. Zhang, X. and Liu, X. (2008) Backward Bifurcation of an Epidemic Model with Saturated Treatment Function. Journal of Mathematical Analysis & Applications, 348, 433-443.
https://doi.org/10.1016/j.jmaa.2008.07.042 - 7. Liu, W.M., Levin, S.A. and Iwasa, Y. (1986) Influence of Nonlinear Incidence Rates upon the Behavior of SIRS Epidemiological Models. Journal of Mathematical Biology, 23, 187-204.
https://doi.org/10.1007/BF00276956 - 8. Zhou, T., Zhang, W. and Lu, Q. (2014) Bifurcation Analysis of an SIS Epidemic Model with Saturated Incidence Rate and Saturated Treatment Function. Journal of Dynamics & Control, 226, 288-305.
https://doi.org/10.1016/j.amc.2013.10.020 - 9. Wiggins, S. (1990) Introduction to Applied Nonlinear Dynamical Systems and Chaos. 2nd Edition, Springer-Verlag, New York.
https://doi.org/10.1007/978-1-4757-4067-7 - 10. Guckenheimer, J. and Holmes, P.J. (1983) Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer-Verlag, New York.
https://doi.org/10.1007/978-1-4612-1140-2