Dynamical Systems and Control
Vol.
09
No.
02
(
2020
), Article ID:
34927
,
8
pages
10.12677/DSC.2020.92011
Dynamic Equation and Numerical Simulation of Nonholonomic Multibody System in Quasi-Coordinate Form
Xin Hao, Yanping Liu, Wenli Yao*
Qingdao Key Laboratory for Geomechanics and Offshore Underground Engineering, College of Science, Qingdao University of Technology, Qingdao Shandong

Received: Mar. 12th, 2020; accepted: Mar. 31st, 2020; published: Apr. 7th, 2020

ABSTRACT
The goal is to study a simpler and more canonical dynamic modeling method for nonholonomic multibody system dynamics and control problems. By using the Euler-Lagrangian form of Gauss principle, the differential equations of dynamic motion suitable for nonholonomic multibody systems in quasi-velocity form are derived. Compared with the dynamic differential equations for nonholonomic systems, which are usually expressed in terms of energy functions and generalized coordinates, the method of derivation presented is simple and direct, and the obtained equations are expressed in explicit matrices of quasi-velocity consistent with the degrees of freedom. It has strong generality and standardization, and is suitable for programming modeling and calculation of multibody system requirements. For the example of nonholonomic system, the differential equation of motion expressed by quasi-velocity is established, and the numerical simulation and the corresponding dynamic characteristics are carried out. Compared with the Routh equation with multipliers, the proposed method is superior in computational speed and can be used to solve the constrained default and location singular problems.
Keywords:Quasi Velocity, Non-Holonomic System, Gauss Principle, Multi-Rigid Body System, Quasi-Coordinate

准坐标形式的非完整刚体系统动力学方程及数值模拟
郝鑫,刘彦平,姚文莉*
青岛理工大学理学院岩土力学与近海地下工程重点实验室,山东 青岛

收稿日期:2020年3月12日;录用日期:2020年3月31日;发布日期:2020年4月7日

摘 要
本文的目标是研究针对非完整多体系统动力学与控制问题的更简单规范的动力学建模方法。采用欧拉–拉格朗日形式的高斯原理推导了适于非完整多体系统的准坐标形式的动力学运动微分方程。与目前常用的以动力学状态函数表达的针对非完整系统的动力学微分方程相比,文中的推导方法简单直接,得到的方程维数与自由度一致,且方程以准速度的显式矩阵表达,具有较强的通用性及规范性,适用于多体系统的程式化建模及计算的要求。针对例子中的典型非完整系统,建立了准速度表达的一阶运动微分方程并进行了数值模拟以及相应的动力学特性分析,与通常用于该类问题的带乘子的Routh方程相比,文中的方法在计算速度上占优,同时在不进行额外的违约修正的前提下,可较好地解决违约及位置奇异问题。
关键词 :准速度,非完整系统,高斯原理,多体系统,准坐标

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
“完整”和“非完整”是力学上对约束和系统的分类概念。完整约束是对系统位形的限制,非完整约束是对系统运动的限制。自从Hertz于1894年首次提出非完整系统的一些重要概念以来,众多学者在非完整系统的基本原理、基本方程及在工程中的应用都取得了重要进展。
非完整系统动力学方程的建立主要依据如下力学原理:1) DLP原理(D’Almbert及Bernoulli原理);2) Gauss原理和Jourdain原理;3) Hamilton原理。其中Gauss原理往往被认为是更具普适性的分析动力学的基本原理 [1]。
在非完整系统动力学的发展过程中,基于上述原理建立起各种不同的动力学方程,这些方程形式各异,一般可以划分为两类:1) 基于乘子理论的动力学方程,如Routh方程 [2] ;2) 约化的不带乘子的动力学方程,如Maggi方程、Appell方程等 [3]。这些方程数学上等价,但数值求解中表现的特性并不相同 [4]。
非完整多体系统的动力学建模主要基于上述几种典型的动力学方程, 上述方程的共同特点是:由表征系统运动状态的某函数(动能、Hamilton函数、加速度能等)及广义力按照规定的微分算子就能得到,思路清晰、表达简洁是其一大优点,但方程的不足之处在于建立了动力学基本函数后,还需经过微分算子的求导运算,对于比较复杂的系统,这种求导运算过程非常冗长。相比而言,Appell方程中的微分算子是最简单的,但建立复杂系统的Appell函数并非易事,Kane通过Jourdain原理,得到用准坐标表达的动力学微分方程,但在求偏速度、广义主动力及广义惯性力的过程涉及到矢量运算,符号复杂运算繁琐 [4] [5] [6] [7]。Udwadia等从Gauss原理出发,得到U-K方程,可以处理一阶非完整系统,但该方程中涉及非常复杂的广义逆矩阵的计算问题 [8] [9] [10]。
高斯原理往往被认为是更具普适性的分析力学的基本原理,可适用于完整、非完整约束系统;同时准坐标表达的方程具有很大的概括性(用广义坐标表达不过是它的特殊情形),而且方程的结果往往很简洁,都是一阶方程。
因此,本文引进了由准坐标表达的坐标系统,采用高斯原理作为基本原理进行了动力学方程的推导。文中得到了以准速度的显式矩阵表达形式的非完整多体系统的动力学微分方程,并以此作为建模的基本方程,研究了非完整系统典型例子的动力学问题,与目前常用的Routh方程的方法进行对比分析,从而探索研究非完整系统动力学与控制问题的更简单规范的建模方法。
2. 准速度、准加速度与广义坐标及广义加速度关系的矩阵表示
设系统由n个广义坐标描述,系统受到g个一阶非完整约束:
(1)
其中m为系统的自由度数,可取后面 个准速度为:
(2)
前面m个准速度可选为以 为变量的m个其它任意函数:
(3)
选择准速度的条件为:(2)和(3)两个式子中所包含的n个函数的Jacobi矩阵 非奇异。
由方程(1) (2)得到广义速度的表达式并微分得到:
(4)
定义下列矩阵:
, , , ,
, , , .
则方程(4)可表达为矩阵形式:
(5)
对(5)求变分,得到:
(6)
3. 以准坐标表示的动力学微分方程
Euler-Lagrange形式的Gauss原理为 [2] [3] :
(7)
将系统动能表达为广义速度的显式:
则(7)式可写为:
(8)
其中 为正定且对称的矩阵, ,其中
为对应系统广义坐标的广义力;
为系数矩阵 的第一类Christoffel符号。
将(5)及(6)代入(8)式,得:
(9)
则(9)式可化为:
(10)
其中:
由于 中元素的独立性,故下式成立:
(11)
则根据准速度的选择方法,准加速度矢量 是m维的,总是与系统的自由度数一致。
4. 例子
如图1,一刚体作平面运动,在其重心C处引与刚体固结的坐标系Cξη约束条件为在任一时刻C点速度恒沿 Cξ 方向,设刚体的质量为M,对C点之惯性矩为IC,求刚体在任意外力作用下的运动 [4]。

Figure 1. Example of nonholonomic systems
图1. 非完整系统的例子
作用在刚体上的外力可简化为主矢量F (设它与x轴间的夹角为 )及对C点的主矩LC。
非完整约束条件为:
(12)
其中xC,yC为C点在固定坐标系Oxy的坐标,φ角为Cξ 轴与x轴间的夹角。令 为广义坐标矢量, 为准速度矢量。
4.1. 基于准速度的高斯最小拘束原理的求解
选择准速度如下:
(13)
则:
因此可通过计算得到下列矩阵:
将A*,g*,Q*代入矩阵方程(11),即:
(14)
通过方程(14)计算得到 ,将其代入(13),可得到广义速度,通过一次积分即可得到下一时
刻的广义坐标的值。
数值计算结果见图2,图3显示了针对约束方程(12)的违约关系图,因准坐标方法中速度约束的自动满足,使得数值结果对约束方程的误差几乎可以忽略。
4.2. 基于Routh方程的求解方法
由非完整系统的Routh方程可以得到:
(15)
方程组(15)连同约束方程(12)式,可以得到系统的动力学解,数值求解结果如图4及图5所示。
4.3. 两种方法的对比分析
a. 基于方程的对比:
采用两种方法所得到的方程分别为(14)及(15),通过消掉方程(15)中的 ,我们可以得出两种方法是数学上等价的;但方程(14)仅含有两个封闭的准加速度方程的微分方程组,而要采用方程(15),需要联立约束方程(12),需要求解包含四个方程的微分代数方程组,显然前者的求解难度要小得多;
由方程(15)的右边项可以看出:
当 时, 没有意义,需要额外处理奇异问题,而方程(14)则避免了此问题。
b. 基于数值运算结果的对比:
图2及图4中,通过两种方法所计算的质心坐标在最初五个波峰前几乎是重合的,从数值层面证明了两种方法的数学等效性;
图3及图5显示了两种方法的速度违约情况,通过对比可知,Routh方法由于速度方程的违约,位移曲线随着仿真时间的增长,其违约程度越来越大。
综上所述,同传统的Routh方法相比,采用准坐标形式的动力学矩阵方程(11)来解决非完整系统的动力学问题,计算速度快,且在不需要额外修正的情况下,可有效地避免违约及位置奇异问题。
5. 结论
同目前常用的以动力学状态函数表达的针对非完整系统的动力学微分方程相比,本文采用高斯原理推导得到了以准坐标形式的动力学微分方程,它以准速度的显式矩阵形式表示,维数与自由度一致,具有较强的通用性及规范性,适用于多体系统的程式化建模及计算的要求。

Figure 2. Relation diagram of centroid coordinates with time (quasi-coordinate method)
图2. 质心坐标随时间变化关系图(准坐标法)

Figure 3. Velocity default graph (quasi-coordinate method)
图3. 速度违约图(准坐标法)

Figure 4. The relation diagram of centroid coordinates with time (Routh method)
图4. 质心坐标随时间变化关系图(Routh法)
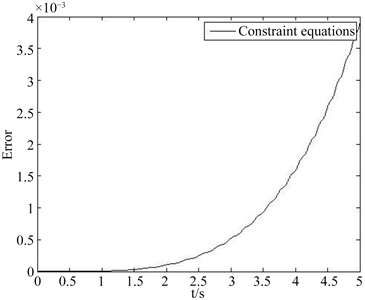
Figure 5. No-revised velocity default graph (Routh method)
图5. 未加修正的速度违约图(Routh法)
文中的准坐标动力学方程同现有的求解非完整约束系统的Routh方程数学上等价,但可不需要额外处理速度违约及位置奇异问题。
本文是对非完整系统动力学与控制问题的更简单规范的建模方法的探索。
文章引用
郝 鑫,刘彦平,姚文莉. 准坐标形式的非完整刚体系统动力学方程及数值模拟
Dynamic Equation and Numerical Simulation of Nonholonomic Multibody System in Quasi-Coordinate Form[J]. 动力系统与控制, 2020, 09(02): 121-128. https://doi.org/10.12677/DSC.2020.92011
参考文献
- 1. 刘才山. 分析动力学中的基本方程与非完整约束[J]. 北京大学学报(自然科学版), 2016, 52(4): 756-766.
- 2. 梅凤翔. 非完整系统力学基础[M]. 北京: 北京工业学院出版社, 1985.
- 3. 刘延柱. 高等动力学[M]. 北京: 高等教育出版社, 2000.
- 4. 陈滨. 分析动力学(第2版) [M]. 北京: 北京大学出版社, 2012
- 5. 黄昭度, 钟奉俄. 工程系统分析力学[M]. 北京: 高等教育出版社, 1992.
- 6. C.A.杰格日达, Щ.X.索尔塔哈诺夫, М.Л.尤士科夫. 非完整系统的运动方程和力学的变分原理[M]. 梅凤翔, 译. 北京: 北京理工大学出版社, 2007.
- 7. 刘恩远. 变质最可控力学系统的Gauss原理和Appell方程[J]. 固体力学学报, 1986, 2.
- 8. Kalaba, R.E. and Udwadia, F.E. (1993) Equations of Motion for Nonholonomic, Constrained Dynamical Systems via Gauss’s Principle. Journal of Applied Mechanic, 60, 662-668.
https://doi.org/10.1115/1.2900855 - 9. Udwadia, F.E. and Kalaba, R.E. (1992) A New Perspective on Constrained Motion. Proceedings of Royal Society A, 439, 407-410.
https://doi.org/10.1098/rspa.1992.0158 - 10. Kozlov, V.V. (2008) Gauss Principle and Realization of Con-straints. Regular and Chaotic Dynamics, 13, 431-434.
https://doi.org/10.1134/S1560354708050055
NOTES
*通讯作者。