Advances in Energy and Power Engineering
Vol.03 No.05(2015), Article ID:16219,16
pages
10.12677/AEPE.2015.35019
Study on the General Accurate Azimuth-Elevation Tracking Angle Formula for Heliostat and Its Applications
Minghuan Guo, Zhifeng Wang
Key Laboratory of Solar Thermal Energy and Photovoltaic System of Chinese Academy of Sciences, IEE-CAS, Beijing
Email: minghuan_guo@163.com, zhifeng@vip.sina.com
Received: Sep. 30th, 2015; accepted: Oct. 23rd, 2015; published: Oct. 26th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
With respect to the widely used azimuth-elevation dual axis tracking heliostats, this paper gives the accurate azimuth-elevation tracking angle formula for a heliostat with a mirror-pivot offset and other six typical geometric error parameters. A nonlinear least-squares mathematical model is established to solve the six typical angular tracking parameters of the azimuth-elevation tracking heliostat based on experimental tracking data, and also gives the two practical numerical solution algorithms. We specially designed a heliostat model and with the help of optical test platform of 3D coordinate measuring machine conducted the indoor laser beam azimuth-elevation tracking experiments. The experimental results validated the general tracking angle formula and the method for estimating the six typical angle error parameters of an azimuth-elevation tracking heliostat. This general accurate azimuth-elevation tracking angle formula can effectively compensate the heliostat pedestal tilt, the initial angle biases of the two rotational axes and the non orthogonal angle error of the two axes and so on. This tracking angle formula has been successfully applied to the 100 heliostats in Badaling 1 MW solar thermal tower power plant (DAHAN solar power plant) in Beijing, China.
Keywords:Heliostat, Azimuth-Elevation Tracking, Tracking Angle Formula
通用的定日镜准确方位–俯仰跟踪公式 及其应用研究
郭明焕,王志峰
中国科学院电工研究所,中国科学院太阳能热利用及光伏系统重点实验室,北京
Email: minghuan_guo@163.com, zhifeng@vip.sina.com
收稿日期:2015年9月30日;录用日期:2015年10月23日;发布日期:2015年10月26日

摘 要
本文针对应用最为广泛的方位–俯仰双轴跟踪定日镜,推导出了“含镜面偏心距和其它6个典型几何误差参数的准确方位–俯仰跟踪公式”,建立了由跟踪实验数据反求定日镜的6个典型角度跟踪参数的非线性最小二乘法数学模型,并给出了2个实用的求解算法。专门设计了一个定日镜模型,并借助三维坐标机的光学测试平台,做了多组室内的激光束方位–俯仰跟踪实验。实验结果很好地验证了跟踪角度公式和估计定日镜的6个典型角度误差参数的方法。该通用的准确方位–俯仰跟踪公式,可有效补偿如定日镜的立柱倾斜、两个旋转轴的非正交等系统误差。定日镜准确跟踪公式,已成功应用于北京八达岭1 MW塔式太阳能热发电站(DAHAN电站)的100台定日镜中。
关键词 :定日镜,方位–俯仰跟踪,跟踪角度公式

1. 引言
定日镜作为塔式太阳能热发电系统中最基本的光学单元,它是由光学反射镜、支撑结构、立柱、传动和跟踪控制系统组成。定日镜通常采用双轴跟踪方式,4种典型的双轴跟踪方式有方位–俯仰跟踪、固定轴水平放置的俯仰-倾斜跟踪、固定轴指向目标位置的自旋–俯仰跟踪和极轴式跟踪,见图1。定日镜双轴跟踪的几何本质是,当定日镜跟踪太阳的时候,旋转中心与镜面中心的连线总与镜面中心的法线重合。也就是说,定日镜无论是采用自旋–俯仰跟踪方式还是方位-俯仰跟踪方式,镜面中心的法向总是相同的。自旋–俯仰跟踪适合于与纠像差的非球面结合,提高平均聚光性能,跟踪结构的成本较高,不适合大规模应用。方位–俯仰跟踪是应用最为广泛的定日镜双轴跟踪方式。俯仰–倾斜双轴跟踪方式,有利于布置较为紧密的定日镜场,提高地面利用率,澳大利亚国家太阳能研究中心的两个塔式系统,采用的就是俯仰-倾斜双轴跟踪方式。极轴式跟踪只适用于单个定日镜应用,不适合用于塔式电站的定日镜场。
DAHAN电站的定日镜场由100面单台反射面积为100 的定日镜组成,每台定日镜由64面正方形单元镜,呈8行8列排布而成,如图2所示。定日镜采用的是方位-俯仰跟踪方式。
如果定日镜的两个旋转轴是相交的,则把两个旋转轴的交点称为定日镜的旋转中心。如果定日镜的镜面中心与旋转中心是重合的,定日镜跟踪太阳时,镜面中心的法向 可以很容易求得,即
可以很容易求得,即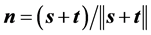 。这里,单位向量
。这里,单位向量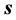 指向太阳,单位向量
指向太阳,单位向量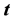 表示从镜面中心指向跟踪目标位置。再根据具体的双轴跟踪的几何关系,就可以方便地从
表示从镜面中心指向跟踪目标位置。再根据具体的双轴跟踪的几何关系,就可以方便地从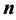 的3个坐标分量中导出固定轴和从动轴的跟踪角度。
的3个坐标分量中导出固定轴和从动轴的跟踪角度。
在实际中,镜面的中心与定日镜的旋转中心并不重合,即镜面参考平面与定日镜的从动轴之间有一定的距离,把这个距离称为镜面的偏心距。遗憾的是,之前还没有针对镜面偏心距的确切的方位-俯仰跟踪公式。给出镜面偏心定日镜的确切的困难在于,在定日镜跟踪太阳的过程中,镜面中心总是在不断移动的。
另外,实际的定日镜总受一些误差因素的干扰,如加工制造的缺陷,或者是环境因素的干扰。因此,在导出确切的方位–俯仰跟踪公式的时候,需要考虑一些典型的几何误差因素。美国的Stone和Jones [1]
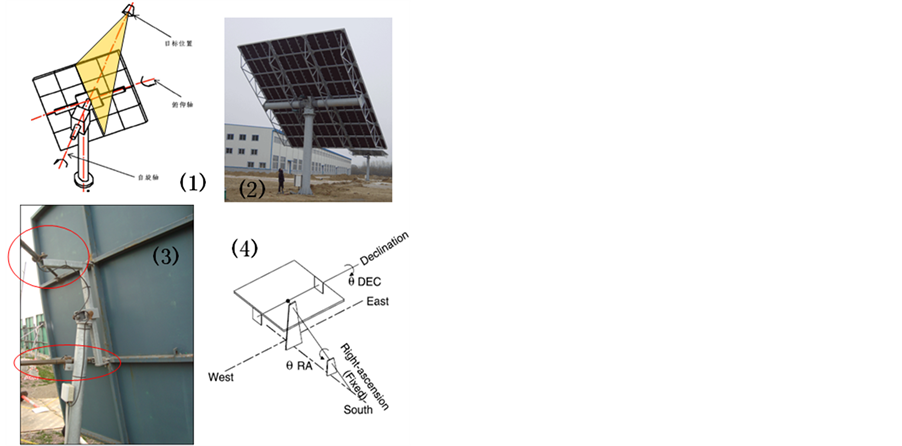
Figure 1. Four typical heliostat dual-axis tracking modes: (1) spinning-elevation or target-oriented, (2) azimuth-elevation, (3) pitch-roll, (4) polar
图1. 四种典型的定日镜双轴跟踪方式:(1) 自旋–俯仰,(2) 方位–俯仰,(3) 俯仰–倾斜,(4) 极轴式
 (a) (b)
(a) (b)
Figure 2. DAHAN heliostat: (a) Heliostat photo; (b) Sketch of heliostat structure
图2. DAHAN电站的定日镜:(a) 定日镜照片;(b) 定日镜结构示意图
列举了定日镜的一些几何误差源,其中包括3个主要的几何误差源,即方位轴的倾斜误差(也叫立柱倾斜)、镜面的倾斜误差(也叫镜面的对齐误差),和编码器的参考位误差,也分析了这些几何误差对定日镜跟踪效果的影响。Chong和Wong [2] 在2009年给出了一个针对碟式太阳跟踪系统的一般方位–俯仰跟踪公式,公式中额外增加了3个跟踪角度参数,不过该公式不涉及补偿镜片偏心距的问题,也只能补偿立柱倾斜误差,而且公式仅限用于最常见的简单太阳位置角度。
定日镜是太阳能塔式热发电的关键聚光单元,跟踪精度是评价定日镜聚光性能的一项重要指标,因此开展定日镜跟踪理论及其应用的研究具有重要意义。
方位–俯仰跟踪定日镜的典型几何误差有镜面偏心距,立柱倾斜的方位角和偏角,两个旋转轴的非正交偏角,镜面平面相对俯仰轴的不平行偏角,两个旋转轴的零位误差(角度),即1个距离误差参数和6个角度误差参数。
这里,首先针对定日镜的镜面偏心距,给出了精确的入射角修正因子,解析表达式可通过求解4次代数方程组得到。为了计算的简洁和方便,又给出了高精度近似解,其精度与理论解几乎无差异,进而给出了定日镜镜面中心准确法向量的表达式。在把镜面中心定义为定日镜旋转中心(2个旋转轴的交点)在镜面平面上的垂直投影的前提下,镜面中心的法向总与旋转中心到镜面中心的连线共线,与具体的双轴跟踪方式无关。
有了镜面中心的准确法向,再经过对应于6个角度误差参数的一系列坐标旋转变换,就可以导出含镜面偏心距和其他典型几何误差参数定日镜的一般方位–俯仰跟踪角度公式。再经过进一步整理和简化,得到完整方位–俯仰跟踪角度公式,只涉及若干步简单的数学计算。
下面针对定日镜的镜面偏心距和其它固定几何误差,给出准确的一般方位–俯仰跟踪公式。
这里讨论的镜面倾斜误差不涉及调整定日镜各个单元镜相对参考平面的倾斜角度,而是指镜面中心的法向偏离要求的法向。镜面参考平面定义为过镜面中心,且与下镜面中心的法向垂直的平面。
由于镜面中心的法向在绕俯仰轴方向的偏离误差与俯仰轴编码器的参考位误差具有一样的跟踪效果,二者区分不开,因此镜面倾斜误差在这里解释为镜片参考平面相对俯仰轴的不平行度,即镜面参考平面与俯仰轴之间的倾斜角度。定日镜的两个旋转轴也可能不严格正交,因此跟踪公式中也包含了俯仰轴与方位轴的垂线之间的偏角。考虑到跟踪轴编码器的参考位误差与方位–俯仰跟踪方式没有直接的几何关系,因此在推导镜面偏心定日镜的准确方位–俯仰跟踪公式的过程中,没有包含跟踪轴的零位误差。
当然,在把方位–俯仰跟踪公式用于实际定日镜时候,就必须确定俯仰轴编码器的参考位和方位轴编码器的参考位。
为了验证本章中给出的针对镜面偏心距的准确方位–俯仰跟踪公式的正确性,专门设计了一个定日镜模型,用来做室内激光束跟踪实验。
2. 镜面偏心定日镜镜面中心的准确法向
对标准的自旋–俯仰跟踪方式,两个旋转轴垂直相交,自旋轴是固定轴,俯仰轴平行于镜面参考平面,且沿着镜面的弧矢方向。作者 [3] 之前已经给出了高精度的自旋–俯仰跟踪公式,用于补偿标准自旋–俯仰跟踪方式中的镜面偏心距。因此,可以用准确自旋–俯仰跟踪公式导出镜面偏心定日镜正常跟踪太阳时镜面中心的准确法向,进而导出带镜面偏心距定日镜的准确方位–俯仰跟踪公式。
2.1. 镜面偏心定日镜的标准自旋俯仰跟踪公式
图3是自旋–俯仰跟踪的几何关系图,图中O表示定日镜的旋转中心,指向目标位置T的向量OT是

 (a) (b)
(a) (b)
Figure 3. Geometry of the standard spinning-elevation tracking heliostat with a mirror-pivot offset: (a) Geometry of spinning-elevation tracking; (b) Angular relationships of heliostat tracking and the residual tracking error in the tracking plane II
图3. 镜面偏心定日镜的标准自旋–俯仰跟踪的几何关系:(a) 自旋–俯仰跟踪的几何关系(未画出镜面偏心);(b) 当前的跟踪平面P内的跟踪角度关系以及跟踪残余误差
自旋轴的指向,ON是镜面中心的法向,OS是太阳位置向量。包含OP0和OT的跟踪平面处在自旋轴的零位位置,并且垂直于地平面;OP0是垂直于OT,并且指向上方。太阳光的入射平面II,也是当前的自旋轴跟踪平面,向量OS、OP、OT和ON都在II内。当OP0绕OT按右手方向转到OP时,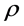 是对应的跟踪自旋角,即∠TON =
是对应的跟踪自旋角,即∠TON =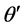 。
。 是名义入射角,∠TON =
是名义入射角,∠TON =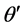 是跟踪仰角,
是跟踪仰角,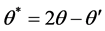 是镜面中心M处的入射角,也等于镜面中心的反射角。与П垂直的俯仰轴和镜面偏心距没有在图3(a)中画出。
是镜面中心M处的入射角,也等于镜面中心的反射角。与П垂直的俯仰轴和镜面偏心距没有在图3(a)中画出。
如图3(b)所示,在太阳光入射平面П内,镜面中心M是旋转中心O在镜面参考平面上的正交投影,镜面偏心距 ,斜向距离
,斜向距离 ,O、M和N共线,
,O、M和N共线,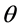 是名义入射角,τ是跟踪仰角修正角,
是名义入射角,τ是跟踪仰角修正角, 是跟踪仰角,
是跟踪仰角,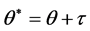 是在镜面中心的太阳光入射角。T1是镜面中心的反射光线与像面(靶面)的交点,T是靶面的中心,靶面与OT垂直。
是在镜面中心的太阳光入射角。T1是镜面中心的反射光线与像面(靶面)的交点,T是靶面的中心,靶面与OT垂直。
如果把OP0、OS、OP、OT和ON的单位向量分别记为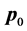 、
、 、
、 、
、 和
和 ,则在左手直角坐标系[O; North-East-Height]下,下面的关系式成立:
,则在左手直角坐标系[O; North-East-Height]下,下面的关系式成立:
 (1)
(1)
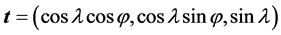 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
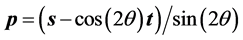 (6)
(6)
 , (当
, (当 时,
时, ) (7)
) (7)
这里,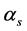 是太阳高度角,
是太阳高度角, 是太阳方位角,l是OT的高度角,φ是OT的方位角,方位角是沿从北到东方向。
是太阳方位角,l是OT的高度角,φ是OT的方位角,方位角是沿从北到东方向。
固定轴指向目标位置定日镜在平面II内的跟踪仰角的一个非常好的高精度近似解为
 (8)
(8)
跟踪仰角 是镜面偏心距Hz和名义入射角
是镜面偏心距Hz和名义入射角 的函数。标准的自旋-俯仰跟踪公式主要由(4)、(5)和(8)组成,镜面中心的准确法向表示为(7)。
的函数。标准的自旋-俯仰跟踪公式主要由(4)、(5)和(8)组成,镜面中心的准确法向表示为(7)。
事实上,精确的修正角τ是方程(9)的解
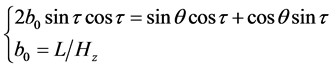 (9)
(9)
方程(9)由可以转化为4次代数方程,
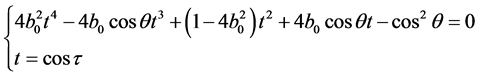 (10)
(10)
方程(10)的解析解如下,
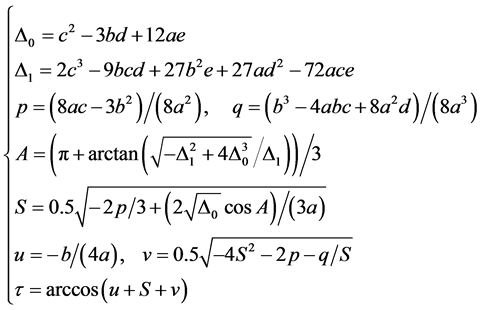 (11)
(11)
显然,解析解(11)远比高精度近似解(8)繁琐,因此在工程应用中推荐使用(8)计算入射角修正角度τ。
2.2. 镜面中心法向的精度
如图3(b)所示,MT与MT1之间的夹角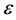 是依赖于
是依赖于 和
和 的跟踪残余误差。根据(8),
的跟踪残余误差。根据(8), 由
由 和L/Hz决定,因此跟踪残余误差
和L/Hz决定,因此跟踪残余误差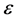 是关于
是关于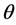 和L/Hz的二元函数。L/Hz 是定日镜旋转中心到跟踪目标位置的斜向距离与镜面偏心距的比值。
和L/Hz的二元函数。L/Hz 是定日镜旋转中心到跟踪目标位置的斜向距离与镜面偏心距的比值。 的计算如下:
的计算如下:
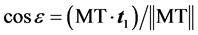 (12)
(12)
 (13)
(13)
 (14)
(14)
 (15)
(15)
跟踪仰角的修正角 由式(8)计算,计算结果显示在如图4(a)中,
由式(8)计算,计算结果显示在如图4(a)中, 的最大值是1.8157˚。跟踪残余误差
的最大值是1.8157˚。跟踪残余误差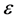 可由(12)~(15)计算,结果显示在图4(b)中。
可由(12)~(15)计算,结果显示在图4(b)中。 的最大值是2.50e-5˚,这比Reda和Andreas给出的太阳位置算法SPA [4] 的极限误差0.0003˚小得多。在典型的CRS聚光场中,L/Hz的最小值一般要大于100,因此对正常的镜面偏心定日镜来说,式(4)、(5)和(8)所给的自旋–俯仰跟踪公式,具有足够高的精度,T1和T几乎是同一个点,(14)是镜面中心的法向的准确表达式。
的最大值是2.50e-5˚,这比Reda和Andreas给出的太阳位置算法SPA [4] 的极限误差0.0003˚小得多。在典型的CRS聚光场中,L/Hz的最小值一般要大于100,因此对正常的镜面偏心定日镜来说,式(4)、(5)和(8)所给的自旋–俯仰跟踪公式,具有足够高的精度,T1和T几乎是同一个点,(14)是镜面中心的法向的准确表达式。
由于镜面中心M的位置可以由镜面中心的法向 确定,即
确定,即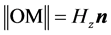 (见(15)),因此只需根据具体的双轴跟踪几何关系,把镜面中心的法向转化成相应的双轴跟踪角度。如果定日镜采用方位–俯仰跟踪方式,便得到镜面偏心定日镜的准确方位-俯仰跟踪公式。
(见(15)),因此只需根据具体的双轴跟踪几何关系,把镜面中心的法向转化成相应的双轴跟踪角度。如果定日镜采用方位–俯仰跟踪方式,便得到镜面偏心定日镜的准确方位-俯仰跟踪公式。
2.3. 镜面中心法向的鲁棒表达式
对于正常跟踪定日镜的镜面中心法向表达式(7)或(14),当名义入射角 接近0时,表达式的数值计算稳定性会变差,因此有必要给出关于镜面中心法向的新的鲁棒表达式[5] 。推导过程如下,
接近0时,表达式的数值计算稳定性会变差,因此有必要给出关于镜面中心法向的新的鲁棒表达式[5] 。推导过程如下,
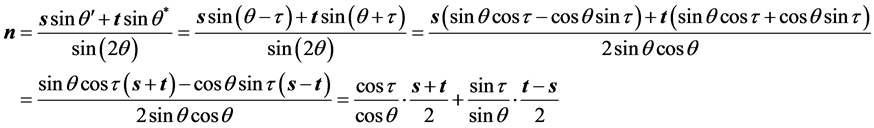
又∵ ,即
,即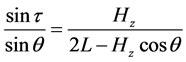
∴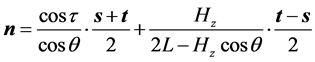 (16)
(16)
3. 镜面偏心定日镜的准确方位–俯仰跟踪公式
3.1. 基于鲁棒镜面中心法向的通用方位–俯仰跟踪公式
要给出的方位–俯仰跟踪公式,不仅包含镜面偏心距,还要包含方位轴相对竖直方向的倾斜、两个旋转轴的非正交度和镜片参考平面相对俯仰轴的不平行度。
图5显示的是镜面偏心定日镜的方位–俯仰跟踪的几何关系,镜面中心的法向ON总是与旋转中心O和镜面中M的连线共线。在图5中, 是定日镜方位轴的倾角,
是定日镜方位轴的倾角,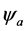 是方位轴的倾斜方位角,II1是定日镜方位轴和俯仰轴确定的双轴平面,
是方位轴的倾斜方位角,II1是定日镜方位轴和俯仰轴确定的双轴平面,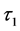 是俯仰轴与垂直于方位轴的直线的偏角,II2 是由俯仰轴和镜面中M确定的平面,
是俯仰轴与垂直于方位轴的直线的偏角,II2 是由俯仰轴和镜面中M确定的平面, 是镜面参考平面相对俯仰轴的倾斜角度,II2 也是局部左手坐标系[O; E1-E2-E3]的E1-E2平面;方位轴沿左手方向旋转,
是镜面参考平面相对俯仰轴的倾斜角度,II2 也是局部左手坐标系[O; E1-E2-E3]的E1-E2平面;方位轴沿左手方向旋转,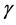 是跟踪方位角,俯仰轴沿右手方向旋转,
是跟踪方位角,俯仰轴沿右手方向旋转,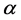 是跟踪仰角。
是跟踪仰角。

 (a) (b)
(a) (b)
Figure 4. Tracking error range of the standard spinning-elevation tracking formula: (a) Calibration angle of tracking elevation angle; (b) Angle of residual tracking error
图4. 标准自旋–俯仰跟踪公式的跟踪误差范围:(a) 跟踪仰角修正角 ;(b) 跟踪误差
;(b) 跟踪误差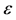
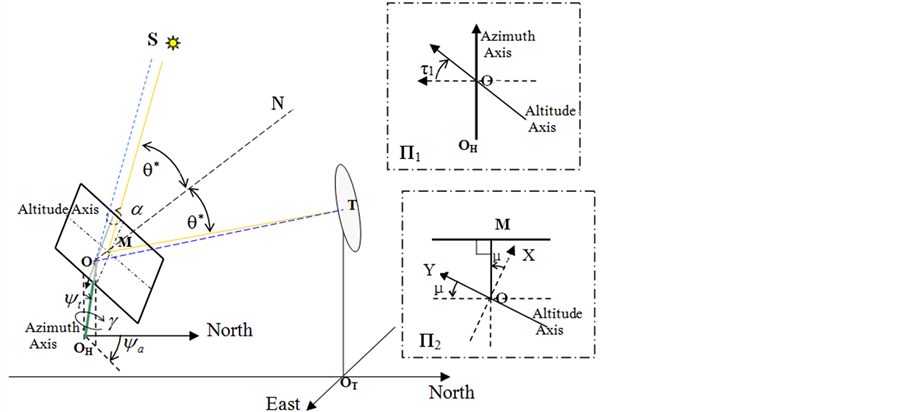
Figure 5. General azimuth-elevation tracking geometry for a heliostat with a mirror-pivot offset and other angular error parameters
图5. 带镜面偏心距和其它角度误差定日镜的一般方位–俯仰跟踪的几何关系
镜面中心的法向ON的E1-E2-E3坐标是 ,而在[O; North-East-Height]坐标系下,由(4)、(8)和(16)算得的镜面中心的法向为
,而在[O; North-East-Height]坐标系下,由(4)、(8)和(16)算得的镜面中心的法向为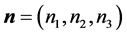 。
。 可以通过顺次施行六次旋转坐标变换转化成
可以通过顺次施行六次旋转坐标变换转化成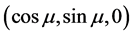 。相对应的,利用左手法则,坐标系[O; North-East-Height]的North轴经过6个连续旋转坐标变换后转到局部坐标系[O; E1-E2-E3]的E1轴位置。6个坐标变换矩阵依次表示如下:
。相对应的,利用左手法则,坐标系[O; North-East-Height]的North轴经过6个连续旋转坐标变换后转到局部坐标系[O; E1-E2-E3]的E1轴位置。6个坐标变换矩阵依次表示如下:
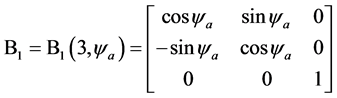
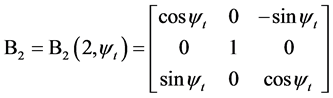
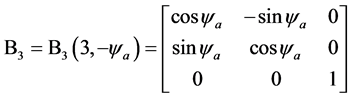
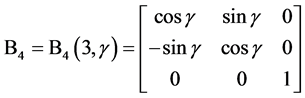
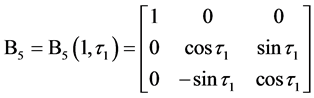
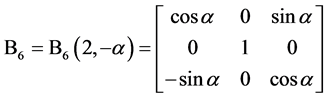
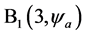 是从起始坐标系([O; North-East-Height])到新坐标系坐标变换矩阵,沿左手方向绕第3个坐标轴旋转角度
是从起始坐标系([O; North-East-Height])到新坐标系坐标变换矩阵,沿左手方向绕第3个坐标轴旋转角度 ;
; 进而把
进而把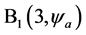 旋转变换后的结果绕第2个旋转轴旋转角度
旋转变换后的结果绕第2个旋转轴旋转角度 ,左手方向是
,左手方向是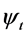 的正方向。可以对旋转坐标变换矩阵
的正方向。可以对旋转坐标变换矩阵 、
、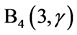 、
、 和
和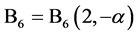 作类似的解释,其中B3中的“-”表示沿右手方向旋转,B6中的“-”表示沿右手方向旋转。
作类似的解释,其中B3中的“-”表示沿右手方向旋转,B6中的“-”表示沿右手方向旋转。
这样,方位-俯仰跟踪的方程可以表示成
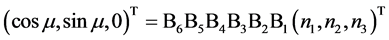 (17)
(17)
再把方程(17)改写为
 (18)
(18)
定义
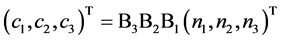 (19)
(19)
则有
 (20)
(20)
 (21)
(21)
比较(20)和(21),便得方位–俯仰跟踪的跟踪仰角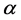 和跟踪方位角
和跟踪方位角 ,即
,即
 (22)
(22)
 (23)
(23)
 (24)
(24)
 (25)
(25)
 (26)
(26)
 (27)
(27)
当 、
、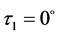 、
、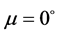 、
、 、
、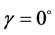 时,定日镜处在竖直位置,镜面中心的法向水平指向正北方,即
时,定日镜处在竖直位置,镜面中心的法向水平指向正北方,即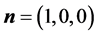 。
。
表达式(4)、(8)、(16)、(19)、(22)~(27)组合起来,完整地给出了镜面偏心定日镜的方位-俯仰跟踪公式。
3.2. 化简后的通用方位–俯仰跟踪公式
上节已经推导出了定日镜准确的通用方位–俯仰跟踪角度公式,里面涉及较复杂的矩阵和向量的数学计算,但是对与普通的工程师来说,使用起来不方便。因此,需要进一步整理和简化,得到完整的方位–俯仰跟踪角度公式,且只涉及若干步简单的数学计算。我们把化简后的方位–俯仰跟踪角度公式记为
 (28)
(28)
公式(28)的逐步计算过程如下,
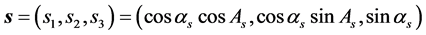
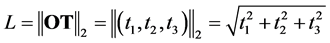
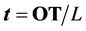
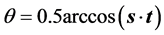
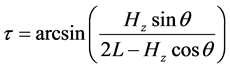
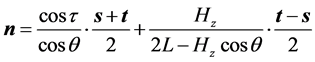
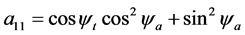
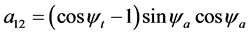
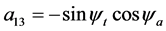
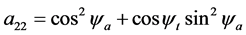
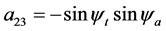
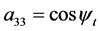
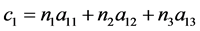
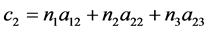
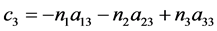
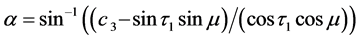
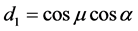
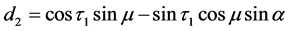
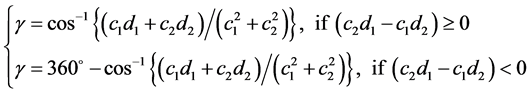
4. 由跟踪实验数据反求定日镜的6个典型角度误差参数
跟踪公式(28)中的跟踪参数,除了镜面偏心距外,还包括了4个典型的几何角度的误差参数,如定日镜方位轴相对竖直方向的倾斜、两个旋转轴的非正交偏角,以及镜面参考平面相对俯仰轴的倾斜角度。此外,在实际的定日镜上使用该通用方位–俯仰跟踪公式的时候,我们还必需确定方位轴编码器和俯仰轴编码器的零位(即与公式中的0°跟踪角度对应的跟踪轴旋转参考位)。
为了使上述的一般方位–俯仰跟踪公式容易用于实际的定日镜,建立了由跟踪实验数据反求定日镜的6个典型角度跟踪参数的非线性最小二乘法数学模型,并给出了2个实用的求解算法[6] 。
最小二乘法数学模型的基本思路是:根据定日镜当前的跟踪方位角、跟踪仰角以及太阳位置向量,求得定日镜镜面中心的法向,进而计算反射太阳光线与目标靶面交点,即得到反射光点在靶面内平面坐标(U-V坐标);再把每组U-V坐标的计算值与观测值的差,作为误差函数,建立最小二乘法数学模型。
4.1. 计算镜面中心的法向
对“带镜面偏心距及其它固定几何误差定日镜的准确方位–俯仰跟踪公式((28))”,若定日镜跟踪方位角的零位角度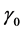 ,跟踪仰角的零。位角度是
,跟踪仰角的零。位角度是 ,即分别用
,即分别用 和
和 代替原来公式中的
代替原来公式中的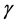 和
和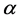 ,则有
,则有
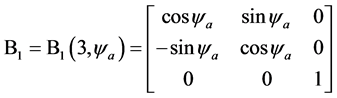
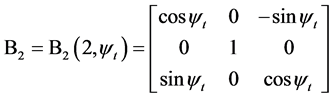
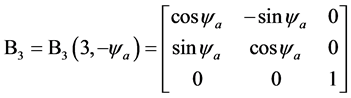
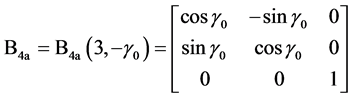
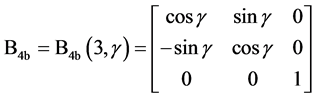
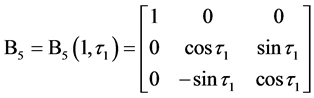
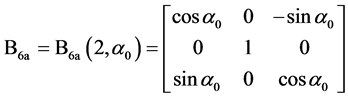
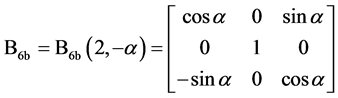
 (29)
(29)
其中, 是定日镜方位轴的倾角,
是定日镜方位轴的倾角, 是方位轴的倾斜方位角,
是方位轴的倾斜方位角, 是俯仰轴与垂直于方位轴的直线的偏角,
是俯仰轴与垂直于方位轴的直线的偏角,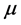 是镜面参考平面相对俯仰轴的倾斜角度,
是镜面参考平面相对俯仰轴的倾斜角度, 是沿左手方向的跟踪方位角,
是沿左手方向的跟踪方位角,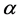 是沿右手方向的跟踪仰角。
是沿右手方向的跟踪仰角。
4.2. 计算镜面中心的反射光线与靶面的交点
根据定日镜当前跟踪方位角、跟踪仰角以及太阳位置向量,求得镜面中心的法向后,就可以计算定日镜镜面中心的反射太阳光线与目标靶面交点,即得到反射光点在靶面内平面坐标(U-V坐标)。图6展示太阳光线在镜面中心反射的几何关系。
如图6,建立以定日镜的旋转中心O (即方位轴与俯仰轴的交点)为原点的左手直角坐标系[O; North-East-Height],M是镜面的中心(即旋转中心在镜面参考平面上的垂直投影),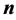 是镜面中心的法向ON的单位向量;T0是靶面坐标系[T0;
是镜面中心的法向ON的单位向量;T0是靶面坐标系[T0;  -
-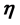 -
-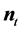 ]的原点,
]的原点, 是靶面的法向,
是靶面的法向, 指向下方,
指向下方,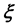 与地面平行,
与地面平行, 、
、 和
和 构成左手直角坐标系;
构成左手直角坐标系; 是单位太阳位置向量,
是单位太阳位置向量,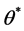 是太阳光线在镜面中心的入射角;T是计
是太阳光线在镜面中心的入射角;T是计
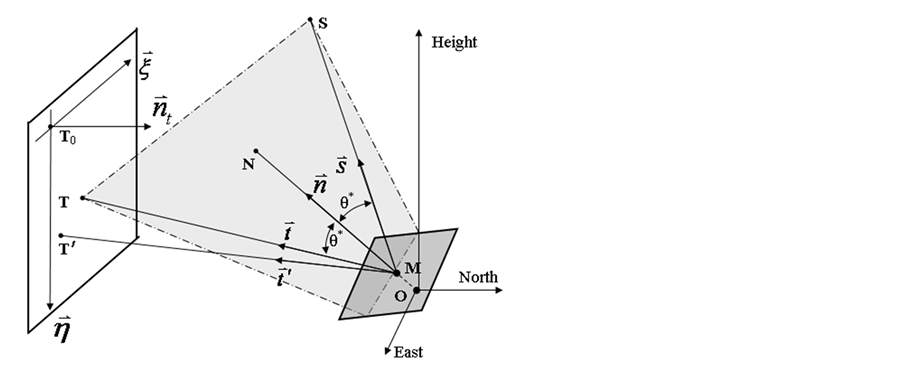
Figure 6. Intersection geometry of the reflected mirror-surface-centre ray with the target plane for a heliostat with a mirror-pivot offset
图6. 过镜面偏心定日镜镜面中心的反射太阳光线与目标靶面相交的几何关系
算出的过镜面中心M的反射太阳光线在靶面上的交点,T'是观测的镜面中心M的反射太阳光线在靶面上的交点; 是向量MT的单位向量,
是向量MT的单位向量, 是向量MT'的单位向量。在靶面坐标系[T0;
是向量MT'的单位向量。在靶面坐标系[T0;  -
- -
- ]下,T和T'的坐标分别为
]下,T和T'的坐标分别为 和
和 ,即
,即 ,
, 。
。
根据(29)求得镜面中心的法向 后,镜面中心的反射光线MT的单位向量
后,镜面中心的反射光线MT的单位向量 计算如下
计算如下
 (30)
(30)
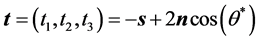 (31)
(31)
向量OT计算如下
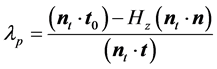 (32)
(32)
 (33)
(33)
从而,
 (34)
(34)
再根据 ,有
,有
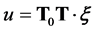 (35)
(35)
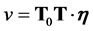 (36)
(36)
4.3. 建立最小二乘法数学模型
为了确定镜面偏心定日镜的方位–俯仰公式中的N = 6个角度跟踪参数 ,需要进行M次方位–俯仰跟踪试验,且
,需要进行M次方位–俯仰跟踪试验,且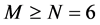 。为了便于书写最小二乘法模型和最小二乘法模型的求解算法,我们记
。为了便于书写最小二乘法模型和最小二乘法模型的求解算法,我们记
 (37)
(37)
设在跟踪实验中,M次 跟踪试验的实验数据为
跟踪试验的实验数据为
太阳位置角度: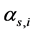 和
和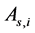 ,
, ;
;
跟踪角度: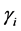 和
和 ,
, ;
;
镜面中心反射光点(镜面中心的反射光线与目标靶面的交点) 的靶面坐标:
的靶面坐标: ,
, 。
。
与 和
和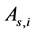 对应的单位太阳位置向量
对应的单位太阳位置向量 ,可由(1)算得。与
,可由(1)算得。与 和
和 对应的镜面中心的法向
对应的镜面中心的法向 ,由(29)计算得到。再由(30)和(31)计算出镜面中心的反射光线的单位向量
,由(29)计算得到。再由(30)和(31)计算出镜面中心的反射光线的单位向量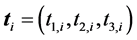 。显然
。显然 和
和 是
是 的函数,即
的函数,即 ,
, ,
,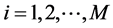 。
。
再根据(32)~(36)计算出镜面中心的反射光线与靶面交点的U-V坐标,记为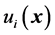 和
和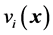 。
。
至此,便得到非线性最小二乘问题的数学模型,误差函数 和目标函数
和目标函数 的表达式如下
的表达式如下
 (38)
(38)
 (39)
(39)
4.4. 两个实用的非线性最小二乘问题求解算法
这里,给出两个实用的非线性最小二乘问题求解算法,即阻尼Gauss-Newton方法和Hartley-Meyer方法,两者都属于修正的Gauss-Newton方法。阻尼Gauss-Newton方法是加了一维搜索后的Gauss-Newton方法。
经反复试验验证,这两种求解方法都表现出良好的收敛特性,对初始值的依赖较弱。这对由带测量误差的跟踪实验数据反求6个典型角度跟踪参数很有利。
阻尼Gauss-Newton方法
给出初始值 ,以及制定精度
,以及制定精度 、
、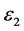 和
和 。
。
Step 1:置 ;
;
Step 2:计算 ;
;
Step 3:计算雅克比矩阵 ,以及
,以及 ;
;
Step 4: ;
;
Step 5:用0.618黄金分割法,反复做一维搜索,确定非负步长因子 ,直到满足
,直到满足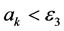 ;
;
Step 6: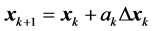 ,并计算
,并计算 ,如果
,如果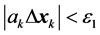 或者
或者 ,则计算结束;
,则计算结束;
Step 7: ,进行Step 2。
,进行Step 2。
最后,目标函数 的极小点和最小值分别是
的极小点和最小值分别是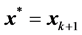 和
和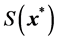 。
。
上面的 表示对N维向量取模,即
表示对N维向量取模,即
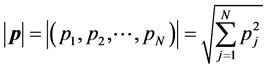
Hartley-Meyer算法
比起阻尼Gauss-Newton方法,Hartley-Meyer方法显得更加简单,也实用。下面给出Hartley-Meyer算法。
给出初始值 ,以及制定精度
,以及制定精度 和
和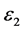 。算法中的信赖域参数
。算法中的信赖域参数 取常数,即
取常数,即 。
。
Step 1:置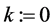 ;
;
Step 2:计算 ;
;
Step 3:计算 ,以及
,以及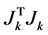 ;
;
Step 4: ;
;
Step 5: ;
;
Step 6: ;
;
Step 7: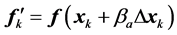 ;
;
Step 8: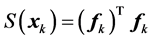 ,
, ;
;
Step 9:如果 ,则
,则 ;
;
否则,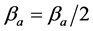 ,进行Step 7;
,进行Step 7;
Step 10: ,并计算
,并计算 ,如果
,如果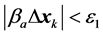 或者
或者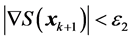 ,则计算结束;
,则计算结束;
Step 11: ,进行Step 2。
,进行Step 2。
最后,得到目标函数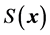 的极小点
的极小点 和最小值
和最小值 。
。
5. 定日镜模型的激光束方位–俯仰跟踪实验
为了验证通用的方位–俯仰跟踪公式的正确性以及由最小二乘法模型确定定日镜的6个角度误差参数方法的有效性,专门设计了一个定日镜模型,并借助三维坐标机的光学测试平台,做了多组室内的激光束方位–俯仰跟踪实验[7] [8] 。实验结果很好地验证了跟踪角度公式和估计定日镜的6个典型角度误差参数的方法。
图7显示的是搭建在三维坐标机测试平台上的激光束方位–俯仰跟踪实验系统。在以定日镜模型的旋转中心O为原点的左手直角坐标系[O; North-East-Height]下,激光束向量为 ,T0 = 0.001 m × (−2593.9, 348.76, 763.79),Hz = 0.129 m,方位轴的倾斜角度为
,T0 = 0.001 m × (−2593.9, 348.76, 763.79),Hz = 0.129 m,方位轴的倾斜角度为 和
和 ,两轴的非正交偏角
,两轴的非正交偏角 ,镜面平面的倾斜角度
,镜面平面的倾斜角度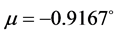 。
。
6. 通用方位–俯仰跟踪公式在北京延庆DAHAN电站的成功应用
定日镜的准确方位–俯仰跟踪公式(28),已成功应用于北京延庆1 MW塔式太阳能热发电站(DAHAN电站)100台定日镜的所有跟踪控制程序中。
下面以图8所示定日镜场中的#12.4和#-9.1两个定日镜为例,展示新的方位–俯仰跟踪公式的应用效
 (a)
(a) (b)
(b)
Figure 7. Azimuth-elevation laser beam tracking test setup for a special designed heliostat model on a CMM platform. (a) Geometry of the heliostat model and laser, (b) Size and position of the target plane
图7. 三维坐标机测试平台上的激光束方位–俯仰跟踪实验系统:(a) 定日镜模型和激光器,(b) 定日镜模型对面的实验靶面
果。每个定日镜一天中可以使用1套(6个)角度误差参数,也可以使用2套角度误差参数,后者一天中上午和下午各使用一套(6个)角度误差参数[9] 。
图9显示定日镜#12.4和#-9.1在一天中的跟踪误差变化情况,比较定日镜在使用通用跟踪角度公式
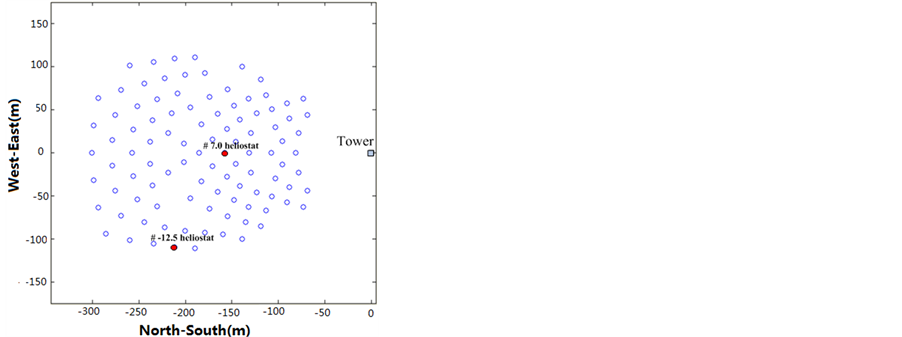
Figure 8. The two test heliostats (#12.4 and #-9.1) in the solar field of the DAHAN solar tower power plant
图8. DAHAN电站定日镜场中的2个实验定日镜(#12.4和#-9.1)
 (a)
(a)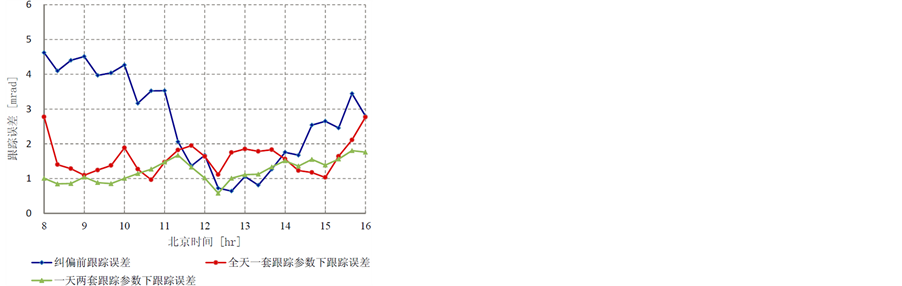 (b)
(b)
Figure 9. The residual tracking error curves of two test heliostats (#12.4 and #-9.1) with different sets of angular tracking parameters in a day
图9. 定日镜在不同跟踪参数模式下的跟踪误差曲线:(a) #12.4定日镜;(b) #-9.1定日镜
前、跟踪公式只用一套跟踪误差参数、跟踪公式中使用2套跟踪误差参数的跟踪误差。
从图9中可以明显看出,定日镜在全天一套跟踪参数下能改善跟踪误差,但是一天两套跟踪参数下(上午用一组角度跟踪参数,下午用另外一组角度跟踪参数)的跟踪效果最好。
基金项目
感谢中国国家自然科学基金项目“大型塔式太阳能电站定日镜场聚光能流密度成像方法(批准号:61450009)”对本研究工作的资助支持,也感谢汉斯出版社期刊编辑部支持免费编辑出版。
文章引用
郭明焕,王志峰. 通用的定日镜准确方位–俯仰跟踪公式及其应用研究
Study on the General Accurate Azimuth-Elevation Tracking Angle Formula for Heliostat and Its Applications[J]. 电力与能源进展, 2015, 03(05): 123-138. http://dx.doi.org/10.12677/AEPE.2015.35019
参考文献 (References)
- 1. Stone, K. and Jones, S. (1999) Analysis of solar two heliostat tracking error sources. Sandia Laboratories, Albuquer-que.
- 2. Chong, K. and Wong, C. (2009) General formula for on-axis sun-tracking system and its application in im-proving tracking accuracy of solar collector. Solar Energy, 83, 298-305. http://dx.doi.org/10.1016/j.solener.2008.08.003
- 3. Guo, M., Wang, Z., Liang, W., Zhang, X., Zang, C., Lu, Z. and Wei, X. (2010) Tracking formulas and strategies for a receiver oriented dual-axis tracking toroidal heliostat. Solar Energy, 84, 939-947. http://dx.doi.org/10.1016/j.solener.2010.02.015
- 4. Reda, I. and Andreas, C. (2004) Solar position algorithm for solar radiation applications. Solar Energy, 76, 577-589. http://dx.doi.org/10.1016/j.solener.2003.12.003
- 5. Guo, M., Sun, F., Wang, Z. and Zhang, J. (2013) Properties of a general azimuth-elevation tracking angle formula for a heliostat with a mirror-pivot offset and other angular errors. Solar Energy, 96, 159-167. http://dx.doi.org/10.1016/j.solener.2013.06.031
- 6. 郭明焕 (2011) 太阳定日镜的误差分析和聚光性能评价方法研究. 博士论文, 中国科学院研究生院, 北京.
- 7. Guo, M., Wang, Z., Zhang, J., Sun, F. and Zhang, X. (2011) Accurate altitude-azimuth tracking angle formulas for a heliostat with mirror-pivot offset and other fixed geometrical errors. Solar Energy, 85, 1091-1100. http://dx.doi.org/10.1016/j.solener.2011.03.003
- 8. Guo, M., Wang, Z., Zhang, J., Sun, F. and Zhang, X. (2012) Determination of the angular parameters in the general altitude-azimuth tracking angle formulas for a heliostat with a mirror-pivot offset based on experimental tracking data. Solar Energy, 86, 941-950. http://dx.doi.org/10.1016/j.solener.2011.12.025
- 9. Sun, F., Guo, M., Wang, Z., Liang, W., Xu, Z., Yang, Y. and Yu, Q. (2015) Study on the heliostat tracking correction strategies based on an error-correction model. Solar Energy, 111, 252-263. http://dx.doi.org/10.1016/j.solener.2014.06.016