Open Journal of Acoustics and Vibration
Vol.
07
No.
01
(
2019
), Article ID:
29226
,
13
pages
10.12677/OJAV.2019.71004
Free Vibration Analysis of Functional Gradient Mindlin Plate of Arbitrary Shape
Yunyan Yu1,2,3*, Xiang Zhu1,2,3, Tianyun Li1,2,3, Wenjie Guo1,4#
1School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan Hubei
2Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics, Wuhan Hubei
3Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai
4Engineering Research Center of Railway Environment Vibration and Noise Ministry Education, East China Jiaotong University, Nanchang Jiangxi

Received: Feb. 16th, 2019; accepted: Mar. 6th, 2019; published: Mar. 13th, 2019

ABSTRACT
In this paper, the free vibration characteristics of functionally graded plates in arbitrary shape were studied based on the improved Rayleigh Ritz method. Assuming that the material of the functionally graded plate changes exponentially along the thickness direction, the vibration of the plate is described by Mindlin plate theory and the improved Fourier series is used as the displacement tolerance function. The energy functional expressions of the functionally graded plate are derived and the natural frequency is obtained by solving them. The convergence and accuracy of the proposed method are verified by compared with the existing literature. Then the proposed method was applied to the triangular and circular plates respectively, in which the versatility of the proposed method was showing. Finally the influences of gradient index, boundary condition and thickness of the functionally graded plate on the free vibration are discussed.
Keywords:Arbitrary Shape, Functionally Graded, Typical Boundary Conditions, Rayleigh-Ritz Method, Improved Fourier Series Method
任意形状功能梯度板的自由振动分析
玉云艳1,2,3*,朱翔1,2,3,李天匀1,2,3,郭文杰1,4#
1华中科技大学船舶与海洋工程学院,湖北 武汉
2船舶与海洋水动力湖北省重点实验室,湖北 武汉
3高新船舶与深海开发装备协同创新中心,上海
4华东交通大学,铁路环境振动与噪声教育部工程研究中心,江西 南昌

收稿日期:2019年2月16日;录用日期:2019年3月6日;发布日期:2019年3月13日

摘 要
本文基于改进的Rayleigh-Ritz法对任意形状功能梯度材料板的自由振动特性进行了分析。假设功能梯度板的材料沿厚度方向指数变化,用Mindlin板理论描述板的振动。引入改进的Rayleigh-Ritz法,利用改进的傅里叶级数作为位移容许函数,结合Mindlin板理论推导得到功能梯度板的能量泛函表达式,根据能量泛函变分原理得到了振动系统的特征方程,求解得到功能梯度板的振动固有频率。通过与文献中功能梯度板的固有频率值对比,验证了本文方法的收敛性与准确性。然后分别对三角形板和圆形板的固有频率进行了求解,表明本文方法的通用性。然后通过算例分析讨论了功能梯度板的梯度指数、边界条件及板厚等参数对固有频率的影响。
关键词 :任意形状,功能梯度,典型边界条件,Rayleigh-Ritz法,改进的傅里叶级数法

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
日本材料学家新野正之,平井敏雄和渡边龙三等人在20世纪80年代中后期提出了功能梯度材料的概念 [1] [2] 。功能梯度材料选择两种不同性能的材料,根据使用要求采用材料复合技术,使中间的组成呈现连续的梯度变化而内部不存在明显的界面,材料的性质和功能沿厚度方向呈梯度变化。这样就可以从材料的本身改善材料的各种性能。由于功能梯度材料具有良好的力学性能,日益成为研究者研究的重点 [3] 。
针对功能梯度材料板壳的振动问题,已经有大量文献开展了研究。王明禄 [4] 考虑了由材料的非均匀性引起的中面应变,求解了固有频率。曹志远 [5] 利用特殊类型各项异性及薄膜弯曲耦联的二维常系数方程研究功能梯度材料圆柱壳的固有频率的解析解。Henry Khov [6] 拓展了选用的位移函数,使其能够精准的满足边界点的控制微分方程。徐坤 [7] 假设剪应力沿厚度方向呈抛物线分布,利用剪切余能与剪切应变能相等原理与虚位移原理及Navier方法研究平板的振动。梁斌 [8] 利用Rayleigh-Ritz方法建立了功能梯度圆柱壳自由振动固有频率的特征方程,其中材料参数为指数型体积分数,推导了一端固定一端自由和两端简支两种基本边界情况下的圆柱壳的自振特性。李伟 [9] 基于哈密顿原理,采用了动力变分方程,并把任意四边边界条件转化为统一的振型参数,对正交各向异性功能梯度开口圆柱壳的固有频率与模态进行求解。陈淑萍 [10] 基于一阶剪切变形理论,求解了两端简支Timoshenko梁自由振动的固有频率,并研究了材料梯度指数对梁动力响应的影响。尹硕辉 [9] 基于一阶剪切变形理论,应用等几何有限元法对功能梯度板进行研究。此外还有大量的数值方法已经得到应用 [12] [13] [14] 。以上研究多是应用解析方法对单一形状的功能梯度板壳的研究,或者是应用数值方法,对于应用解析方法对任意形状功能梯度板壳问题的研究成果还非常少。
本文采用改进的Rayleigh-Ritz法,基于一阶剪切理论对功能梯度材料板的自由振动进行研究。考虑材料沿厚度方向梯度指数变化的功能梯度板,引入改进的Rayleigh-Ritz法,利用改进的傅里叶级数和Mindlin板理论推导得到功能梯度板的能量泛函表达式,求解得到功能梯度板的振动固有频率。通过数值算例的计算并和文献对比证明本方法的收敛性与准确性,然后对其他形状板的自由振动进行了求解。
2. 理论模型
2.1. 功能梯度材料
对于功能梯度材料板结构,通常研究其材料属性沿厚度方向的变化。采用空间连续函数模型,则由两种材料组成的功能梯度材料沿厚度方向材料组分的分布规律:
(1)
其中, 为功能梯度材料的物理属性如密度、杨氏模量等, 和 为两种组分材料的物理属性, 和 为两种材料的体积分数,且满足:
(2)
采用幂函数形式,则体积分数表示为:
(3)
式中k为梯度指数。代入式(1)可得
(4)
2.2. 改进的Rayleigh-Ritz法
改进的Rayleigh-Ritz法与传统的Rayleigh-Ritz法相比的改进之处在于对边界条件的处理以及位移容许函数的选取方法。
2.2.1. 函数域的拓展
对Rayleigh-Ritz法中的函数域进行扩展,模型如图1。

Figure 1. Calculation model of arbitrary shaped plate
图1. 任意形状板的计算模型
S为薄板的求解域,Sa为试函数的积分域,长度分别为Lx和Ly。当求解域S为任意的不规则形状时,可以假想将结构域扩展为一个略大于真实域的矩形域Sa,矩形域要涵盖待求取结构的真实求解域。一般来说,取求解域距x、y轴最大距离作为矩形域的边界。当采用改进的傅里叶级数作为结构的试函数时,使用矩形域能更便捷地构造出合理的试函数。而在求板的应变能、动能时,只需对真实求解域进行离散并积分,然后求取泛函极值得到振动方程。
2.2.2. 曲边边界的虚拟弹簧处理方法
经典的边界条件,比如固支和简支等往往不能准确模拟结构的实际边界,对于实际边界条件,可采用弹簧模型,通过在结构域的边界上采用平动弹簧和转动弹簧来模拟弹性边界。以矩形板为例施加弹簧边界,如图2所示。

Figure 2. Model of rectangular plate
图2. 矩形板物理模型
假设平动弹簧和转动弹簧刚度值分别为kij(N/m)和Kij(Nm/rad),各种复杂边界条件可通过设置两种弹簧的刚度值模拟。经典边界条件下的刚度值如表1所示。模拟弹性边界条件时则将刚度系数取为相应的值即可。
表1. 经典边界条件下的边界弹簧取值
通过弹性边界设置,这将任意边界对结构振动的影响转化为边界弹簧的弹性势能对结构总刚度的影响。
3. 公式推导
功能梯度板的振型函数可以表示为:
(4)
其中Amn,Bmn,Cmn为未知系数, , 分别为与x、y有关的函数, 为时间因子,在下文中忽略。
本文方法选用改进的傅里叶级数作为试函数 [11] ,具体形式为:
(5a)
(5b)
其中 ; 。由于改进的傅里叶级数可以满足任意边界条件,使板的试函数在整个求解域内三阶导数连续且四阶导数各点均存在,可以有效克服边界处可能出现的不连续现象。
考虑到材料沿厚度不均匀分布会导致物理中面的改变,引入 表示新物理中面的位置。
(6)
其中 为弹性模量,随厚度变化。
考虑物理中面位置改变,由中厚板的Mindlin理论可以得到位移的形式:
(7)
应力与应变的关系可以表示为:
(8)
(9)
其中 为沿厚度方向变化的剪切模量。
外力与应力的关系为:
(10)
将式(7)~(9)代入式(10)中可得:
(11)
式中Gb为弯曲刚度,Gs为扭转刚度:
(12)
(13)
式中k0为截面校正因子,本文中取k0 = 5/6。
设
(14)
(15)
将式(14)和(15)代入式(7)中可得:
(16)
则中厚板的动能为:
(17)
式中 为单位面积密度。
(18)
则中厚板的弯曲应变能可以相应地表示为:
(19)
式中
(20)
采用弹簧模型处理边界条件,则三种弹簧组成的弹簧刚度系数矩阵为
(21)
其中kl为平动弹簧的刚度值,kxl为 的转动弹簧刚度值,kyl为
的转动弹簧刚度值,kyl为 的转动弹簧刚度值。
的转动弹簧刚度值。
功能梯度板的边界弹簧势能表示为:
(22)
于是系统的能量泛函为:
(23)
对未知系数求极值:
(24)
求解式(24)并将所得结果整理化简,于是可将振动问题转化为求解特征值的问题:
(25)
其中 为圆频率。
4. 数值计算
4.1. 材料属性
本节算例中考虑如下几种材料,材料属性如表2所示。考虑两种功能梯度材料,分别为Al/Al2O3和Al/ZrO2。
4.2. 收敛性分析
由前文分析可知,计算过程中存在针对级数的求和,因此计算结果的准确性受到截断项数M和N的影响。此外在用弹簧模拟诸如刚性固定等边界时,实际弹簧刚度取值也不可能取无穷大,因此需要对截断项数及弹簧刚度系数的取值进行收敛性分析。
Table 2. Properties of materials
表2. 材料属性
在算例中选取了功能梯度矩形板作为计算模型,如图2所示。分别选用四边自由和四边刚性固定的条件进行收敛性分析。模型参数如下:材料为Al/Al2O3,长为a = 1 m,宽为b = 1 m,厚h = 0.1 m,材料梯度指数k = 1。
首先分析截断项数M和N的收敛性,考虑四边自由板,取kl和K为0,M和N从10取到15,固有频率大小随M和N的变化如表3所示。由表3可知,当M = N = 14时,结构的各阶固有频率不再随着M和N的增加而变化,此时计算结果已收敛。
Table 3. Natural frequencies of rectangular plate (Hz), F-F-F-F
表3. 四边自由(F-F-F-F)边界条件下功能梯度矩形板固有频率随截断项数的变化(Hz)
然后将板的四边设置为固支约束,取M = N = 14,且K和kl的值从1012变化到1020,以验证K和k的收敛性,得到的固有频率如表4所示。表4中数据表明,当弹簧的刚度系数不断增大时,固支功能梯度矩形板的弯曲自由振动的频率逐渐增大后趋于稳定。当弹簧的刚度系数达到kl = 1014时结果已经收敛。故可以取上述数值模拟弹簧刚度系数为无穷大时的取值。
Table 4. Natural frequencies of rectangular plate (Hz), C-C-C-C
表4. 四边固支(C-C-C-C)功能梯度矩形板固有频率随弹簧刚度值变化(Hz)
4.3. 准确性验证
本小节计算不同边界条件下,不同厚度的功能梯度矩形板的无量纲频率,将无量纲频率与已有的文献结果对比,验证本方法在求解功能梯度板的振动的准确性。
选用边长为a = 1 m,b = 1 m,厚度分别为h = 0.05、0.1、0.2 m的功能梯度矩形板,材料为Al/Al2O3。计算简支功能梯度矩形板的无量纲频率 ,与文献 [15] 进行比对,如表5所示。
Table 5. Natural frequency parameters of rectangular plate, (S-S-S-S, Al/Al2O3, a/b = 1)
表5. 四边简支(S-S-S-S)功能梯度矩形板无量纲固有频率(材料Al/Al2O3, a/b = 1)
更换材料为Al/ZrO2,计算无量纲频率 ,与文献 [16] 进行比对。如表6所示:
Table 6. Natural frequency parameters of rectangular plate ( γ = ω a 2 ρ m / E m / h , S-S-S-S, h = 0.1, a/b = 1)
表6. 简支边界下功能梯度矩形板无量纲固有频率( ,S-S-S-S,h = 0.1,a/b = 1)
表5、表6中结果表明,对各种材料、厚度的功能梯度板,本文的计算结果与文献均吻合很好,说明了本方法的准确性。
4.4. 功能梯度三角形板的弯曲自由振动特性分析
本节对功能梯度三角形板进行弯曲自由振动特性分析,板为边长分别为 ,
,c = 2 m的等腰直角三角形,h = 0.1 m,材料为Al/Al2O3,计算其简支边界条件下的固有频率,换算为无量纲频率
,
,c = 2 m的等腰直角三角形,h = 0.1 m,材料为Al/Al2O3,计算其简支边界条件下的固有频率,换算为无量纲频率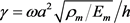 ,如表7。
,如表7。
Table 7. First six natural frequency parameters of triangular plate under different gradient index
表7. 不同梯度指数下功能梯度三角形板前六阶无量纲固有频率
4.5. 功能梯度圆形板的弯曲自由振动分析
对功能梯度圆形板进行弯曲自由振动的特性分析,圆板的几何参数为半径R = 1 m,h = 0.1 m,材料为Al/Al2O3,计算简支边界条件下的固有频率,换算为无量纲频率,如表8,从表中可见随着梯度指数增大,相同阶的固有频率逐渐降低。
Table 8. First six natural frequency parameters of circle plate under different gradient index
表8. 不同梯度指数下功能梯度圆形板前六阶无量纲固有频率
4.6. 梯度指数k对功能梯度板的固有频率影响分析
本节讨论功能梯度指数、边界条件和板厚等对固有频率的影响。
首先讨论梯度指数对频率的影响与不同的边界条件的关系。选用边长a = 1,b = 1,厚度h = 0.1的功能梯度板,材料为Al/Al2O3,边界分别为四边固支、四边简支、一边固支三边自由。求无量纲频率,作图3。
从图3可以看出,随着梯度指数增大,首阶固有频率逐渐降低,但是降低的程度随梯度指数增大趋于平缓,且从不同边界条件的三条曲线可见,梯度指数相同时,四周固支板固有频率最高,一边固支板固有频率最低。
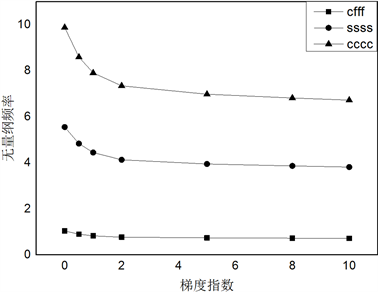
Figure 3. Curves of the first-order dimensionless natural frequency of rectangular FGM plate with gradient index under different boundary conditions
图3. 不同边界条件下功能梯度矩形板首阶无量纲固有频率随梯度指数变化的曲线
以下为四边简支功能梯度板为例,讨论梯度指数对无量纲频率的影响以及与固有频率阶数的关系。几何和材料参数和上一算例相同。图4为前三阶固有频率随梯度指数变化的曲线。

Figure 4. Curves of the first three-order dimensionless natural frequency of rectangular FGM plate, S-S-S-S
图4. 功能梯度矩形板前三阶无量纲固有频率随梯度指数变化的曲线,S-S-S-S
从图4中看出,功能梯度板的前三阶固有频率随梯度指数的变化趋势基本相同,随梯度指数增大,固有频率逐渐降低,这是由于梯度指数增大,板的等效刚度逐渐降低。同时也可以得出功能梯度指数对板的低阶固有频率的影响与阶数基本无关。
以下讨论梯度指数对频率的影响与板的厚度的关系。选用边长a = 1 m,b = 1 m,厚度分别为h = 0.05 m、0.1 m、0.2 m的简支功能梯度板,材料为Al/Al2O3,得到图5在不同板厚下的无量纲频率随梯度指数变化的曲线。
从图5中可以看出,对于不同厚度的功能梯度板,材料梯度指数的变化对其自由振动首阶频率的影

Figure 5. Curves of the first-order dimensionless natural frequency of rectangular FGM plate with gradient index under different thicknesses
图5. 不同板厚下功能梯度矩形板首阶无量纲固有频率随梯度指数变化的曲线
响大致相同。板厚越大,首阶固有频率越高。
5. 结论
本文基于改进的Rayleigh-Ritz法研究了任意形状功能梯度板的振动。引入改进的傅里叶级数作为结构的位移容许函数,基于一阶剪切理论,计算结构的应变能和动能,利用弹簧模拟边界条件的方法对任意形状边界上的支撑条件进行处理,通过求取系统控制方程的特征值,计算得到结构的固有频率。通过算例对比验证了方法的准确性,然后计算了三角形和圆形功能梯度板的固有频率,讨论了梯度指数、边界条件等对固有频率的影响。
文章引用
玉云艳,朱 翔,李天匀,郭文杰. 任意形状功能梯度板的自由振动分析
Free Vibration Analysis of Functional Gradient Mindlin Plate of Arbitrary Shape[J]. 声学与振动, 2019, 07(01): 28-40. https://doi.org/10.12677/OJAV.2019.71004
参考文献
- 1. Niino, M. (1987) Functionally Gradient Materials as Thermal Barrier for Space Plane. Journal of the Japan Society for Composite Ma-terials, 13, 257-264. ://doi.org/10.6089/jscm.13.257
- 2. Koizumi, M. (1993) The Concept of FGM. Cerzmic Trans. Function-ally Gradient Materials, 34, 3-10.
- 3. 李华东, 朱锡, 梅志远, 张颖军. 功能梯度板壳的力学研究进展[J]. 材料导报, 2012, 26(1): 110-118.
- 4. 王明禄, 魏高峰, 李翠艳. 功能梯度材料梁的自由振动问题研究[J]. 山东轻工业学院学报(自然科学版), 2009, 23(3): 19-21.
- 5. 曹志远. 功能梯度复合材料圆柱壳基本理论及长壳固有振动解[J]. 玻璃钢/复合材料, 2006(4): 3-6.
- 6. Khov, H., Li, W.L. and Gibson, R.F. (2009) An Accurate Solution Method for the Static and Dynamic Deflections of Ortho-tropic Plates with General Boundary Conditions. Composite Structures, 90, 474-481. ://doi.org/10.1016/j.compstruct.2009.04.020
- 7. 徐坤, 陈美霞, 谢坤. 正交各向异性功能梯度材料平板振动分析[J]. 噪声与振动控制, 2016, 36(4): 14-20.
- 8. 梁斌, 李戎, 张伟, 徐红玉. 功能梯度材料圆柱壳的振动特性研究[J]. 船舶力学, 2011, 15(Z1): 109-117.
- 9. 李伟柏, 曹志远, 唐寿高. 正交各向异性功能梯度材料开口圆柱壳的自由振动分析[J]. 力学季刊, 2016, 37(3): 433-440.
- 10. 陈淑萍, 赵红晓, 耿少波, 武晋文. 功能梯度材料Timoshenko型剪切梁的自由振动分析[J]. 材料科学与工程学报, 2018, 36(1): 112-116.
- 11. 尹硕辉, 余天堂, 刘鹏. 基于等几何有限元法的功能梯度板自由振动分析[J]. 振动与冲击, 2013, 32(24): 180-186.
- 12. Bhangale, R.K. and Ganesan, N. (2006) Free Vibration of Simply Supported Functionally Graded and Layered Magneto-Electro-Elastic Plates by Finite Element Method. Journal of Sound & Vibration, 294, 1016-1038. ://doi.org/10.1016/j.jsv.2005.12.030
- 13. 王青山, 史冬岩, 罗祥程. 任意边界条件下矩形板的面内自由振动特性[J]. 华南理工大学学报(自然科学版), 2015, 43(6): 127-134.
- 14. Gilhooley, D.F., Batra, R.C., Xiao, J.R., et al. (2007) Analysis of Thick Functionally Graded Plates by Using Higher-Order Shear and Normal Deformable Plate Theory and MLPG Method with Radial Basis Functions. Composite Structures, 80, 539-552. ://doi.org/10.1016/j.compstruct.2006.07.007
- 15. Zhao, X., Lee, Y.Y. and Liew, K.M. (2009) Free Vibration Analysis of Functionally Graded Plates Using the Element-Free kp-Ritz Method. Journal of Sound and Vibration, 319, 918-939. ://doi.org/10.1016/j.jsv.2008.06.025
- 16. Hosseini-Hashemi, Sh., Rokni Damavandi Taher, H., Akha-van, H. and Omidi, M. (2010) Free Vibration of Functionally Graded Rectangular Plates Using First-Order Shear Deformation Plate Theory. Applied Mathematical Modelling, 34, 1276-1291. ://doi.org/10.1016/j.apm.2009.08.008
