非等时距MGM (1, N)优化算法在工程测量中的应用 Application of Optimization Algorithm for Unequal Time Interval MGM (1, N) in Engineering Survey

doi:10.12677/GST.2020.82009

Geomatics Science and Technology
Vol. 08 No. 02 ( 2020 ), Article ID: 35219 , 10 pages
10.12677/GST.2020.82009

Application of Optimization Algorithm for Unequal Time Interval MGM (1, N) in Engineering Survey

Pengfei Ge

●How to Cite this Article

Shanghai Municipal Engineering Design Institute, Shanghai

Received: Apr. 2^nd, 2020; accepted: Apr. 16^th, 2020; published: Apr. 23^rd, 2020

ABSTRACT

The coefficients matrix of the errors in variables model with both fixed column elements, random elements and non-random elements was considered by introducing the structure matrix, the optimization algorithm was used to solve the parameters of the non-equidistant multivariable grey model. It was applied to the fitting and prediction of the deformation monitoring of the building site above the old goaf. The experimental results show that the proposed algorithm is effective and feasible. In addition, the accuracy of multivariate grey model is higher than that of univariate grey model, because the multivariate grey model takes into account the temporal and spatial correlation of deformation data series.

Keywords:Errors in Variables, Structure Matrix, Total Least Square, Gauss-Hermett, Grey Model

非等时距MGM (1, N)优化算法在工程测量中的应用

葛鹏飞

上海市政总院，上海

收稿日期：2020年4月2日；录用日期：2020年4月16日；发布日期：2020年4月23日

摘要

通过引入结构矩阵，兼顾了变量含误差模型中系数矩阵同时存在固定列元素、随机元素、非随机元素的情形，并用于非等时距多变量灰色模型参数的优化求解，将优化算法应用于老空区上方建筑场地变形监测的拟合和预报中，实验结果表明本文算法是有效且可行的。另外，由于多变量灰色模型兼顾了变形数据序列的时空关联性，故多变量灰色模型精度高于单变量灰色模型。

关键词 :变量含误差，结构矩阵，总体最小二乘，高斯–赫尔墨特，灰色模型

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

最小二乘 [1] (Least squares)自提出以来在数据拟合、参数求解方面有着广泛应用，但其仅考虑观测向量误差，在当前的数据处理中，该模型显得不够完善。而基于变量含误差模型(Errors in variables)的总体最小二乘(Total least square, TLS)能兼顾观测量和系数矩阵两方面误差，Gloub与Van Loan [2] 最早于1980年在数值分析领域提出TLS的概念，并提出了基于奇异值分解(SVD)的TLS解法。在测绘领域，总体最小二乘广泛应用于回归参数拟合 [3]、坐标转换 [4] 当中。经过数十年的发展，TLS在解法及形式上有着丰富的研究成果，Schaffrin [5] 运用拉格朗日原理首次提出了总体最小二乘迭代法，文献 [6] 证明了总体最小二乘迭代解法与奇异值分解法的等价性；最早基于奇异值分解的TLS解法没有考虑系数矩阵存在常数列，混合总体最小二乘 [7] (LS-TLS)很好的解决了这一问题，进一步考虑到系数矩阵非常数列元素之间存在重复元素，结构总体最小二乘(STLS) [8]、混合结构总体最小二乘(MLS-STLS) [9]、虚拟总体最小二乘(VTLS) [10] 对这一问题又进行了解决，文献 [9] 对混合结构总体最小二乘迭代解法进行了详细的推导；而加权总体最小二乘 [11]、稳健加权总体最小二乘 [12] 分别考虑了观测量与系数矩阵元素不等精度，原始数据含有粗差的情况，这使总体最小二乘有了更进一步的完善。

在非线性理论的快速发展下，变形监测理论和方法也得到了进一步的丰富和发展，根据变形监测知识可知，在实际监测中，前期的监测点位布设以及后续的实际量测，所遵循的要求就是能尽量反映变形体的变形特征来。即变形体的变形特征需要多个监测点的监测数据来综合呈现，某单一的监测数据仅是变形特征的一个分量。这就充分证明各监测点在一定范围内是相互联系、协同发展的，表现出明显的空间相关性，这种相关性在实际工程测量数据中尤为常见。为此，本文将影响实际变形的时间相关性与空间相关性同时予以考虑，对非等时距多变量灰色模型的建模机理及应用展开研究，分析了建模过程中模型的本质为EIV模型，进而采用顾及系数矩阵误差的总体最小二乘优化算法对其进行优化处理。

2. 非线性高斯赫尔默特模型的混合结构总体最小二乘算法

总体最小二乘法的函数模型为：

$L + e_{L} = (A + E_{A}) X$ (1)

上式中 $e_{L}$ 、 $E_{A}$ 分别为观测向量 $L$ 和系数矩阵 $A$ 的误差向量和误差阵。定义其随机模型为：

观测向量与系数矩阵等精度情形：

$[\begin{matrix} e_{L} \\ v e c (E_{A}) \end{matrix}] ~ N {[\begin{matrix} 0 \\ 0 \end{matrix}], σ_{0}^{2} [\begin{matrix} I_{m} & 0 \\ 0 & I_{n} \otimes I_{m} \end{matrix}]}$ (2.1)

观测向量与系数矩阵不等精度情形：

$[\begin{matrix} e_{L} \\ v e c (E_{A}) \end{matrix}] ~ N {[\begin{matrix} 0 \\ 0 \end{matrix}], σ_{0}^{2} [\begin{matrix} Q_{L L} & 0 \\ 0 & Q_{A A} \end{matrix}]}$ (2.2)

式中 $v e c (E_{A})$ 表示将 $E_{A}$ 按列拉直转换为 $m n \times 1$ 的列向量， $\otimes$ 为矩阵的克罗内克积算子， $σ_{0}$ 为单位权中误差。为表达方便，现令 $e_{A} = v e c (E_{A})$ ，根据最小二乘法平差约束准则，直接给出总体最小二乘法的平差约束准则为：

$e_{L}^{T} e_{L} + e_{A}^{T} e_{A} = m i n$ (3)

考虑到系数矩阵可能同时含有常数列、随机元素、固定元素，通过引入结构矩阵 $D$ ，此时模型可表达为：

$A X - L = [\begin{matrix} I_{n} & - (X_{p} \otimes I_{n}) \cdot D \end{matrix}] [\begin{matrix} e_{L} \\ e_{a} \end{matrix}]$ (4)

上式中 $X_{p}$ 为模型中系数矩阵为非固定列对应的模型参数， $e_{a}$ 为按列提取系数矩阵非固定列所有函数独立的随机元素的改正数构成一个列向量，为推导方便，令

$M = [\begin{matrix} I_{n} & - (X_{p} \otimes I_{n}) \cdot D \end{matrix}]$ , $e = [\begin{matrix} e_{L} \\ e_{a} \end{matrix}]$ (5)

根据总体最小二乘的高斯赫尔默特模型(4)、平差准则(3)，构造目标函数如下

$Φ (e, λ, X) = e^{T} P e + 2 λ^{T} (L - A X + M \cdot e)$ (6)

根据拉格朗日条件极值原理，则有目标函数对各估计量求偏导等于零，并求解方程组得模型参数估值为：

$X = {({(A + E_{A})}^{T} {(M Q M^{T})}^{- 1} A)}^{- 1} {(A + E_{A})}^{T} {(M Q M^{T})}^{- 1} L$ (7)

上式求逆部分显然不对称，有文献指出这种不对称更容易导致逆矩阵不存在，因此给上式两端同乘

${(A + E_{A})}^{T} {(M Q M^{T})}^{- 1} A$ 之后，再同时加上 ${(A + E_{A})}^{T} {(M Q M^{T})}^{- 1} E_{A} X$ 得

$X = {[{(A + E_{A})}^{T} {(M Q M^{T})}^{- 1} (A + E_{A})]}^{- 1} {(A + E_{A})}^{T} {(M Q M^{T})}^{- 1} (L + E_{A} X)$ 。 (8)

3. 非等时距序列MGM模型优化

3.1. 非等时距序列GM (1, 1)模型建模机理 [13] [14]

假设在不同时刻 $t_{k}$ 观测得到的一组原始序列数据为 $x^{(0)} = {(x^{(0)} (t_{1}), x^{(0)} (t_{2}), \dots, x^{(0)} (t_{n}))}^{T}$ ，令

$Δ t_{k} = t_{k} - t_{k - 1}, k = 2, 3, \dots, n$ (9)

当 $Δ t_{k}$ 不为常数时，即两相邻时刻的时间差不固定，此时原始数据序列 $x^{(0)}$ 为非等间隔观测序列，一次累加生成序列如下式：

$x^{(1)} (t_{k}) = \sum_{i = 1}^{k} Δ t_{i} x^{(0)} (t_{i}), k = 1, 2, \dots, n, Δ t_{1} = 1$ (10)

进行逆运算，得到对应的累减还原式子为

$x^{(0)} (t_{k}) = \frac{x^{(1)} (t_{k}) - x^{(1)} (t_{k - 1})}{Δ t_{k}}, k = 2, 3, \dots, n$ (11)

对一次累加生成序列 $x^{(1)}$ 建立一阶微分方程，对微分方程进行积分并离散化处理得：

$x^{(0)} (t_{k}) + a_{1} z^{(1)} (t_{k}) = b_{1}$ (12)

对上式进行积分得到该模型的时间响应序列为：

$x^{(1)} (t_{k}) = \frac{b_{1}}{a_{1}} + (x^{(9)} (t_{1}) - \frac{b_{1}}{a_{1}}) \cdot e^{- a_{1} (t_{k} - t_{1})}$ (13)

根据最小二乘平差准则，在 $v^{T} v = \min$ 条件下，按下式平差解算可以获取灰参数的最优无偏估值。

$X = {(A^{T} A)}^{- 1} A^{T} L$ 。(14)

3.2. 非等时距多变量灰色模型MGM (1, N)建模机理 [13] [14]

MGM (1, N)模型考虑了多个变量相互影响和发展的变形情况，完全不同于GM (1, N)，也不是GM (1, 1)模型的简单叠加，而是GM (1, 1)模型在N元变量情况下的拓展，通过建立N个N元微分方程，联立求解MGM (1, N)模型中的灰参数，而多个变量之间的相互影响程度便反映在所求灰参数中，灰参数主导模型的整个拟合和后续的预测过程。

设有n个相互关联的变形监测点，分别在 $k_{1}, k_{2}, \dots, k_{m}$ 时刻对其进行了监测，即监测周期为m。第j个监测点在 $k_{i}$ 时刻对应的监测数据表示为 $x_{j}^{(0)} (k_{i})$ ，m个周期的监测数据序列 $_{j}^{(0)}$ 表示为：

$X_{j}^{(0)} = {[\begin{matrix} x_{j}^{(0)} (k_{1}) & x_{j}^{(0)} (k_{2}) & \dots & x_{j}^{(0)} (k_{m}) \end{matrix}]}^{T}$ (15)

则n个监测点m期观测数据可用矩阵表示为：

$X^{(0)} = {[\begin{matrix} x_{1}^{(0)} & x_{2}^{(0)} & \dots & x_{n}^{(0)} \end{matrix}]}^{T}$ (16)

其中，若相邻两监测时刻的时间差 $Δ k_{i} = k_{i} - k_{i - 1}$ 不为常量，则称 $X^{(0)}$ 为非等时距序列。非等时距MGM (1, N)模型的一阶白化微分方程组为

$\frac{d X^{(1)} (t)}{d t} = C_{1} X^{(1)} (t) + C_{2}$ (17)

式中 $C_{1}$ 、 $C_{2}$ 即为非等间距MGM (1, m)模型的参数矩阵。同理，进行积分运算可得到MGM (1, N)模型的时间响应函数为：

$X^{(1)} (t_{k}) = (C_{1}^{- 1} C_{2} + X^{(0)} (t_{1})) \cdot e^{C_{1} (t_{k} - t_{1})} - C_{1}^{- 1} C_{2}$ (18)

需要指出的是：式中 $e^{C_{1} (t_{k} - t_{1})}$ 为矩阵指数函数，令 $Δ = t_{k} - t_{1}$ ，其物理意义为第k期观测与第一期观测之间的周期间隔，往往为整数，因此可按下式计算

$e^{C_{1} Δ} = I + C_{1} Δ + \frac{C_{1}^{2}}{2!} Δ^{2} + \dots = I + \sum_{i = 1}^{\infty} \frac{C_{1}^{i}}{i!} Δ^{i}$ (19)

为获取模型参数 $C_{1}$ 、 $C_{2}$ ，可将式(17)离散化得到非等间距MGM (1, N)模型差分方程

$x_{j}^{(0)} (t_{k}) = \sum_{i = 1}^{n} a_{j i} z_{i}^{(1)} (t_{k}) + b_{j} (j = 1, 2, \dots, n; k = 2, 3, \dots, m)$ ，写成矩阵形式为

$Y = L \cdot H$ (20)

其中 $Y = [\begin{matrix} x_{1}^{(0)} (2) & x_{2}^{(0)} (2) & \dots & x_{n}^{(0)} (2) \\ x_{1}^{(0)} (3) & x_{2}^{(0)} (3) & \dots & x_{n}^{(0)} (3) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ x_{1}^{(0)} (m) & x_{2}^{(0)} (m) & \dots & x_{n}^{(0)} (m) \end{matrix}]$ ， $L = [\begin{matrix} z_{1}^{(1)} (2) & z_{2}^{(1)} (2) & \dots & z_{n}^{(1)} (2) & 1 \\ z_{1}^{(1)} (3) & z_{2}^{(1)} (3) & \dots & z_{n}^{(1)} (3) & 1 \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\ z_{1}^{(1)} (m) & z_{2}^{(1)} (m) & \dots & z_{n}^{(1)} (m) & 1 \end{matrix}]$ ， $H = [\begin{matrix} C_{1}^{T} \\ C_{2}^{T} \end{matrix}]$ ，认为n

个监测点的m期监测数据独立等精度获得，则根据经典最小二乘原理可得参数解为

$H = {(L^{T} L)}^{- 1} L^{T} Y$ 。 (21)

3.3. 建模优化

可以看出无论是非等时距多变量灰色模型MGM (1, N)还是GM (1, 1)，采用模型进行拟合和预报的精准性完全取决于所求模型参数的精度。而以上两种模型的系数矩阵 $L$ 均由两部分构成，一部分是由原始数据序列经过紧邻均值计算后得到的，另一部分则是由一列全为1的列向量组成，如果原始数据序列含有误差扰动时，系数矩阵 $L$ 的前一部分必然也是受误差扰动影响的。而传统的获取多变量灰色模型参数解的方法是仅考虑原始数据序列 $Y$ 的误差，通过多元最小二乘法解得的，显然这是不严密的。因此，可将系数矩阵 $L$ 和观测量矩阵 $Y$ 含有的误差同时考虑进来，并顾及系数矩阵中含有常数列的情况，采用上文介绍的总体最小二乘法求取模型的参数值，以达到对参数值的优化，进而提高模型的拟合和预报精度。

4. 案例分析(Examples Analysis)

为分析采空区上方高速公路建设场地残余变形特征，为此，沿高速公路路线方向布设沉降监测点，残余沉降监测自2013年11月起，截至2014年8月，获取了不等时间间隔观测10个周期的沉降数据，累计时长263天，为满足建模要求，首先需将沉降数据进行非负性处理，处理后的原始数据序列见表1。

Table 1. Original data series

表1. 原始数据序列

对以上原始数据分别建立非等间隔GM (1, 1)模型、非等间隔MGM (1, 3)模型，并分别采用传统方法以及本文提到的优化算法求取模型参数，之后将参数代入模型获取实验数据的拟合值和预测值，最终从模型参数的求取精度、实验数据的拟合均方误差以及预测值的残差大小三方面对以上两种模型及参数优化方法进行评价。具体方案设计如下：

A方案：对选取的J89、J90、J91三个水准监测点的9期监测数据建立各自的非等间距GM (1, 1)模型，分别采用最小二乘法和上文中提到的总体最小二乘法进行模型参数求取，并建立相应的时间响应函数，进行拟合和预测；

B方案：对选取的J89、J90、J91三个水准监测点的9期监测数据建立非等间距MGM (1, 3)模型，分别采用最小二乘法和上文中提到的总体最小二乘法进行模型参数求取，并建立相应的时间响应函数，进行拟合和预测。

为比较非等间距GM (1, 1)模型中传统最小二乘算法与总体最小二乘优化算法优劣，将A方案的部分实验结果分别列于表2、表3，表2为针对J89、J90、J91三个水准监测点建立的非等间距GM (1, 1)模型，并分别采用传统最小二乘法和总体最小二乘优化算法所求取的模型灰参数值，以及平差结果的单位权中误差。表3为将J90号点两种算法所求取的模型参数带入模型后，算得的拟合值和预报值以及拟合误差和预报误差。

Table 2. Calculation results of GM (1, 1) model parameters in scheme A

表2. 方案A中GM (1, 1)模型参数计算结果

Table 3. Fitting error of point J90 of two algorithms under scheme A

表3. 方案A下两种算法J90号点拟合误差

为比较非等间距MGM (1, 1)模型中传统最小二乘算法与总体最小二乘优化算法优劣，对B方案进行实施，需要指出的是，在建立非等间距MGM (1, 3)模型之前，首先对所选取的J89、J90、J91三个水准监测点的监测数据序列进行关联度分析，本次采用斜率关联度计算公式算得J89与J90序列间、J90与J91序列间、J89与J91序列间的关联度分别为0.92、0.97、0.92，这表明三个数据序列之间有很强的关联性，完全满足建模要求。建立好相应的非等间距MGM (1, 3)模型后，分别采用传统最小二乘法和本章的优化算法进行参数求取，所求模型参数及单位权中误差见表4。为进一步比较分析两种算法在模型进行拟合和预测两方面的效果，将所求参数代入模型，建立相应的时间响应函数，将两种方法所得的拟合值、预测值以及拟合误差、预测误差分别列于表5、表6。

Table 4. Calculation results of MGM (1, 3) model parameters in scheme B

表4. 方案B中MGM (1, 3)模型参数求取结果

Table 5. Residual error of least squares parameter fitting in scheme B

表5. 方案B中最小二乘求参拟合残差

Table 6. Total least squares fitting residuals in scheme B

表6. 方案B中总体最小二乘拟合残差

为比较分析非等间隔GM (1, 1)模型、非等间隔MGM (1, 3)模型的拟合和预报效果，以总体最小二乘的求参结果为准，将J89、J90、J91三点的拟合误差以及预报误差制成柱状图列于图1、图2、图3。

Figure 1. Fitting/prediction error of two models of J89

图1. J89号点两种模型的拟合/预报误差

Figure 2. Fitting/prediction error of two models of J90

图2. J90号点两种模型的拟合/预报误差

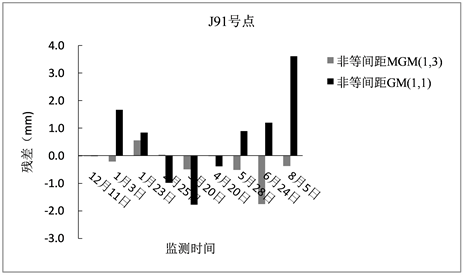
Figure 3. Fitting/prediction error of two models of J91

图3. J91号点两种模型的拟合/预报误差

从表2可以看出，对于J89、J90、J91三点建立的非等间距GM (1, 1)模型，采用传统最小二乘法和总体最小二乘法的平差结果差异较小，其中发展系数a的值完全相同，而控制系数b的值略有不同，单位权中误差基本一致。从表3可以看出，比较分析J90点前七组数据的拟合均方误差来说，总体最小二乘算法优于最小二乘算法，但并不显著，而对于后两组数据的预报误差来说，总体最小二乘算法并不优于最小二乘。从此算例的实验结果来看，两种算法均能获取相同的发展系数a，而a代表了原始数据序列的发展态势，对于有限的数据来说这种结果是完全合理的，从单位权中误差以及拟合误差来看，总体最小二乘算法的优越性没有得到显著体现，而其预报效果明显低于传统算法，这与总体最小二乘理论上更严密的结论相违背，分析原因可能是针对本算例的实验数据，模型本身精度有限，顾及系数矩阵误差的总体最小二乘算法对模型的改进被模型误差所掩盖，其优越性得不到体现。

从表4可以看出，针对J89、J90、J91三点建立的非等间距MGM (1, 3)模型，采用传统最小二乘法和多元总体最小二乘优化算法的平差结果有所差异，采用优化算法计算的单位权中误差明显小于传统算法，这是因为优化算法顾及了系数矩阵中非随机元素所含的误差，使得平差模型更加严密，故所求模型参数的精度更高；比较表5、表6中的数据可以看出，无论是前七组建模数据的拟合误差还是后两组数据的预报误差，基于多元总体最小二乘的优化算法均小于传统的多元最小二乘算法，这进一步表明了优化算法较传统算法的严密性和优越性。

经过上述分析，在非等间距GM (1, 1)模型的求解中优化算法和传统算法效果相当，在非等间距MGM (1, 3)模型的求解中优化算法有一定的优越性。因此，统一以总体最小二乘优化算法为准，比较J89、J90、J91三点在两种模型下的拟合和预报效果，从图1、图2、图3中可以看出各点在非等间距MGM (1, 3)模型下的拟合误差和预报误差均明显小于非等间距GM (1, 1)模型，这是由于多变量灰色模型MGM (1, 3)不仅考虑了变形数据序列的时间相关性，还考虑了监测点的空间相关性，使得所建立的模型更能贴切的反映变形数据之间相互影响的发展态势。这也相应的证明了在此算例中非等间距GM (1, 1)模型具有较大的模型误差，从而佐证了关于总体最小二乘优化算法在非等间距GM (1, 1)模型求解中，其优越性得不到体现的解释的正确性。

5. 结论

1) 将文中算法应用于高速公路建设场地残余沉降的拟合和预报，实验结果表明：混合结构总体最小二乘平差方法对于非等时距GM (1, 1)模型参数的优化效果并不明显，对非等时距MGM (1, N)模型参数的优化效果比较明显。

2) 由于非等时距多变量灰色模型MGM (1, N)兼顾了变形数据序列的时间、空间相关性，建立的模型更能贴切的反映变形数据之间相互影响的发展态势，故此，该模型的拟合和预报精度均明显高于非等时距单变量灰色模型GM (1, 1)。

文章引用

葛鹏飞. 非等时距MGM (1, N)优化算法在工程测量中的应用
Application of Optimization Algorithm for Unequal Time Interval MGM (1, N) in Engineering Survey[J]. 测绘科学技术, 2020, 08(02): 68-77. https://doi.org/10.12677/GST.2020.82009

参考文献

1. 武汉大学测量平差组. 误差理论与测量平差基础[M]. 第2版. 武汉: 武汉大学出版社, 2003: 71-74.

2. Gloub, G.H. and Van Loan, F.C. (1980) An Analysis of the Total Least Squares Problem. SIAM Journal on Numerical Analysis, 17, 883-893. https://doi.org/10.1137/0717073

3. 鲁铁定, 陶本藻, 周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报(信息科学版), 2008(5): 504-507.

4. 方兴, 曾文宪, 刘经南, 姚宜斌. 三维坐标转换的通用整体最小二乘算法[J]. 测绘学报, 2014(11): 1139-1143.

5. Schaffrin, B. and Felus, Y.A. (2007) Multivariate Total Least-Squares Adjustment for Empirical Affine Transformations. Proceedings of the 6th Ho-tine-Marussi Symposium for Theoretical and Computational Geodesy, Vol. 132, 238-242. https://doi.org/10.1007/978-3-540-74584-6_38

6. 鲁铁定, 周世健. 总体最小二乘的迭代解法[J]. 武汉大学学报(信息科学版), 2010(11): 1351-1354.

7. 鲁铁定, 周世健, 王乐洋. 混合总体最小二乘的迭代解算算法[J]. 数据采集与处理, 2015(4): 802-809.

8. 王鼎, 张莉, 吴瑛. 基于角度信息的结构总体最小二乘无源定位算法[J]. 中国科学(F辑: 信息科学), 2009(6): 663-672.

9. 胡川, 陈义, 彭友. 混合结构总体最小二乘参数估计[J]. 大地测量与地球动力学, 2013(4): 56-60.

10. 魏二虎, 殷志祥, 李广文, 李智强. 虚拟观测值法在三维坐标转换中的应用研究[J]. 武汉大学学报(信息科学版), 2014(2): 152-156.

11. 袁庆, 楼立志, 陈玮娴. 加权总体最小二乘在三维基准转换中的应用[J]. 测绘学报, 2011(S1): 115-119.

12. 陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012(5): 715-722.

13. 党耀国, 王正新, 钱吴永, 等. 灰色预测技术方法[M]. 北京: 科学出版社, 2014.

14. 肖新平, 毛树华. 灰预测与决策方法[M]. 北京: 科学出版社, 2013.

期刊菜单