Journal of Sensor Technology and Application
Vol.06 No.02(2018), Article ID:24534,10
pages
10.12677/JSTA.2018.62007
Study on the Simulation of Planar Coil Oil Grinding Sensor
Xinjie Zhong1, Yanxue Wang2
1Guilin University of Electronic Technology, Guilin Guangxi
2Beijing University of Civil Engineering and Architecture, Beijing

Received: Apr. 5th, 2018; accepted: Apr. 19th, 2018; published: Apr. 26th, 2018

ABSTRACT
Mechanical failures are mostly caused by the wear particles in the equipment. Detection of wear particles in the oil can effectively reflect the state of mechanical equipment. Online oil debris monitoring technique can effectively detect the concentration and the size of abrasive particle in the oil, thereby it can successfully monitor condition of mechanical equipment. When a particle passed through the sensor, the magnetic field of the sensor will be changed. An oil debris sensor with planar coil model has been established using ANSYS Maxwell software in this work. Two aspects of the transient and steady states of the model have been analyzed. Research on the influences of different parameters on the sensor in the steady state and the variation of abrasive passing through the sensor have been thoroughly conducted. The results of simulation have important meanings for the parameter optimization of oil debris sensor with planar coil.
Keywords:Oil Debris, Finite Element Method, Planar Coil, Sensor
平面线圈油液磨粒传感器仿真研究
仲昕杰1,王衍学2
1桂林电子科技大学,广西 桂林
2北京建筑大学,北京

收稿日期:2018年4月5日;录用日期:2018年4月19日;发布日期:2018年4月26日

摘 要
机械设备发生故障,大多数是由机械设备中磨损颗粒引起的。油液中的磨损颗粒可以直接反应出机械设备的状态。油液磨粒在线监测技术可以有效的检测油液中磨粒的浓度与大小,从而确定机械设备运行的状态。磨损颗粒穿过油液磨粒检测传感器时,会使传感器产生的磁场发生变化。本文应用ANSYS Maxwell软件建立了一个平面线圈油液磨粒检测传感器模型,并对其进行了瞬态和稳态两方面有限元仿真分析,得到了稳态时传感器不同参数对检测效果的影响以及瞬态时磨粒穿过平面线圈传感器的磁场变化规律。研究结果对于平面线圈油液磨粒检测传感器参数优化具有重要的意义。
关键词 :油液磨粒,有限元分析,平面线圈,传感器

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
大型机械设备在运行中出现的安全事故,往往会造成重大的人员伤亡以及财产的损失,因此对大型机械设备的检测是极其重要的。机械装备的故障发生大多数都是由机械磨损而造成的 [1] 。有资料表明,约80%轴承、齿轮故障是由于摩擦磨损和润滑失效造成的 [2] [3] 。为了使机械设备安全、可靠地运行,通常需要通过振动分析进行故障的早期诊断,进而做出合理的诊断与维修决策 [4] 。对机械进行故障检测分析的手段分为离线(off-line)、在线(on-line)、全在线(inline)三种采样检测方式 [5] 。
国防科技大学对电磁式磨粒传感器内部磁场进行了研究,建立了三线圈传感器模型,通过实验数据验证了该传感器理论模型的正确性 [6] 。军械工程学院对此也进行了相当丰富的研究,对磨粒在电磁式磨粒传感器中径向分布对电感变化的影响进行了深入分析,探讨了铁磁质磨粒形状对传感器电感变化的影响 [7] 。海军工程大学的张永祥教授致力于超声波监测磨粒技术的研究,提出了一种聚焦超声传感器设计准则 [8] 。武汉理工大学殷勇辉、严新平利用油液中磨粒的光散射特性监测油液中所含的固体颗粒大小以及污染度的监测仪器,设计的正交光纤在线监测油液中颗粒以及油液污染度的监测器申请了专利 [9] 。南京航空航天大学的卞利等运用静电传感器在线监测机械设备润滑油中磨损颗粒的荷电情况,以及利用显微成像及计算机视觉技术获取污染油液中颗粒图像的方法,通过图像处理获取颗粒的尺寸及其分布情况,从而实现油液污染度的监测 [10] 。2007年,美国阿克隆大学的Li Du,和Jiang Zhe等人开始对单线圈电感式油液磨粒传感器进行研究。他提出了一种基于电感式库仑计数原理,并具有高输出通量特点的单线圈油液磨粒传感器 [11] 。
上述所提到的各类传感器的设计,仍是现阶段所需要研究的方向。本文采用文献 [12] 中提出的平面线圈油液磨粒传感器结构,应用ANSYS Maxwell软件对平面线圈传感器进行了模型的建立与有限元分析,主要研究了稳态下不同参数的平面线圈数传感器的磁场分布,瞬态下金属磨粒穿过传感器时的磁场变化。为平面线圈传感器参数优化提供借鉴。
2. 平面线圈有限元分析理论基础
19世纪英国物理学家詹姆斯–麦克斯韦建立了一组描述电场、磁场与电荷密度、电流密度之间的偏微分方程,称之为麦克斯韦方程组。它由麦克斯韦-安培定律、法拉第电磁感应定律、高斯定律和高斯磁定律四个公式组成。
麦克斯韦–安培定律:
(1)
式(1)中H为磁场强度,i为电流密度。
法拉第电磁感应定律:
(2)
式(2)中E为电场强度。
高斯定律:
(3)
式(3)中D为电位移矢量,ρ为电荷密度。
高斯磁定律:
(4)
式(4)中B为磁通量密度。
有限元仿真的理论基础基本上都是由麦克斯韦方程组推到出来。相关的电磁场分析就是针对麦克斯韦方程组的参数进行分析的。
根据毕奥-萨法尔定律:
(5)
式(5)中I为通过导体的电流大小, 为单位向量, 为真空磁导率。
单匝的平面线圈空间磁场分布如图1所示。
图1中 为线圈的半径,I为线圈通过的电流, 为空间上任意一点,取线圈上任意一电流元 ,则空间任意一点p点在x,y,z方向上的磁感应强度大小为:
(6)
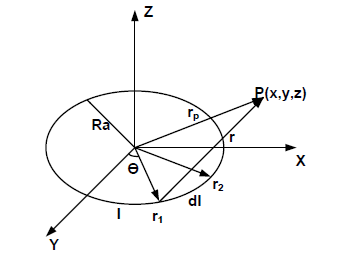
Figure 1. Magnetic field distribution
图1. 磁场分布图
(7)
(8)
3. 平面线圈有限元分析分析
3.1. 稳态分析
平面螺旋线圈油液磨粒传感器通过施加激励源时,它是径向产生磁场;而三线圈油液磨粒传感器是轴向产生磁场。当磨损颗粒穿过平面螺旋线圈油液磨粒传感器时,它产生的径向磁场会发生变化,因此需要一个较小的区域来感应磨损颗粒;而磨损颗粒穿过三线圈传感器时,它是轴向的磁场产生变化,从而使感应线圈产生的感应电压产生变化。
平面螺旋线圈油液磨粒传感器模型的建立,可等效为一个一个单匝的线圈叠加而成,其匝数为30匝,内径为4 mm,横截面直径为0.3 mm,线距为0.3 mm。应用ANSYS Maxwell软件对其进行建模,如图2所示。
平面线圈稳态分析主要是用铜和空气这两种材料,ANSYS Maxwell软件有属于自己的材料库,线圈设置成铜copper材料,属性用默认的;其他的全部用空气air材料,属性也用默认的。
网格划分是有限元分析的重要部分,好的网格划分能减少运算时间并增加结果的精准度。ANSYS Maxwell软件网格划分主要有两个部分,1) 自动划分,2) 手动划分。本章由于模型精简,因而用的是网格自动划分。
在ANSYS Maxwell软件Maxwell 3D模块中施加激励源时,可以在模型的所需施加激励源的一个部位划分出一个剖面,在这个剖面上施加激励源。在平面线圈中给每个线圈施加一个电流大小为1 A,方向相同的激励源。
最后进行分析计算,当分析计算结束后可以根据各种操作命令得到各种所需的结果图。如图3所示。
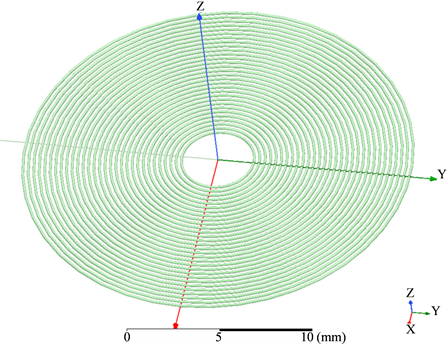
Figure 2. Wear particle sensor 3-D model
图2. 传感器三维图
 (a)
(a)
 (b)
(b)
 (c)
(c)
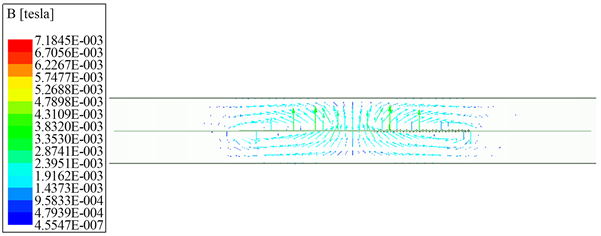 (d)
(d)
Figure 3. Simulation result
图3. 仿真结果图
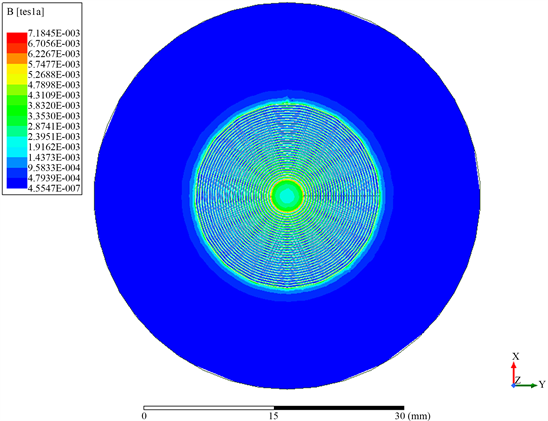
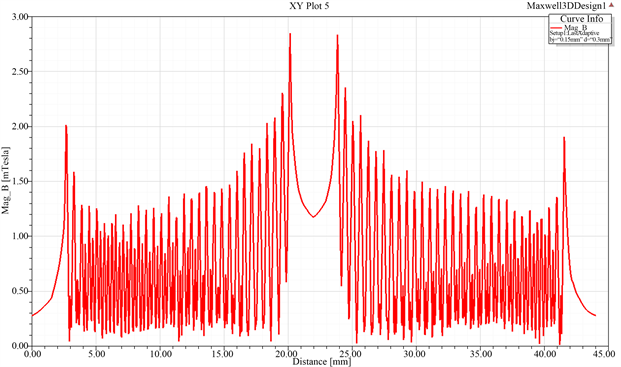
其中图(a)为平面线圈在XOY平面的磁场分布云图,图中可以看出每个线圈产生的磁场都会互相叠加和互相抵消,最里面的线圈产生的磁场由于内部没有磁场预制抵消,所以磁场式最强的。图(b)为平面线圈在YOZ平面的磁场分布曲线图,由于每个线圈都施加了独立的激励源,因此每个线圈都会产生独立的磁场,而相邻的线圈所产生的部分磁场会相互抵消,所以线圈与线圈之间的磁场分布曲线会成锯齿型。由于最里面的线圈产生的靠近里面的磁场没有磁场与之抵消,所以磁场强度为最大。图(c)为平面线圈在YOZ平面的磁场分布云图。图(d)为平面线圈在YOZ平面的磁场矢量图。
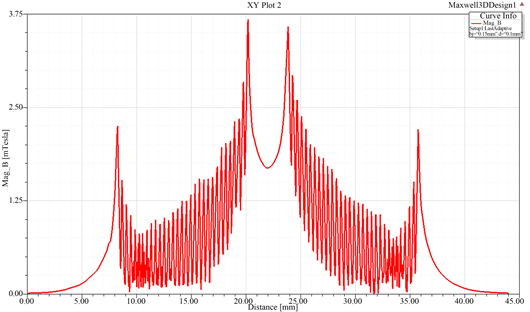
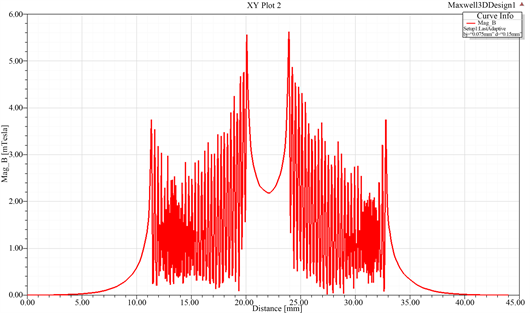
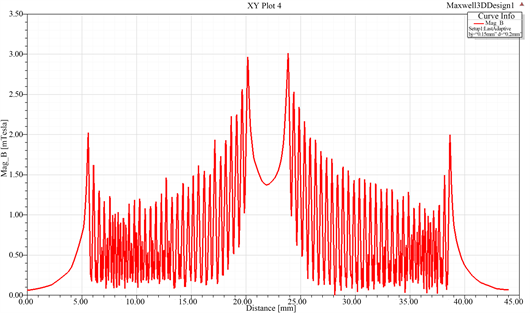
图4所示为不同参数下的平面线圈YOZ平面上的磁场分布曲线图,(a)为线圈横截面直径是0.15,线圈的间距为0.15;(b)为线圈横截面直径是0.3,线圈间距为0.1;(c)为线圈横截面直径为0.3,线圈间距为0.2。
为了更直观的观察和比较不同参数下平面线圈YOZ平面上的磁场分布曲线,将图3(b)和图4中(a)(b)(c)这四幅图拟合成一幅图,如图5所示。
图5中红色曲线为线圈横截面直径是0.15,线圈的间距为0.15的曲线图;黑色曲线为线圈横截面直径是0.3,线圈的间距为0.1的曲线图;蓝色曲线为线圈横截面直径是0.3,线圈的间距为0.2的曲线图;绿色曲线为线圈横截面直径是0.3,线圈的间距为0.3的曲线图。当激励源和匝数相同的情况,线圈间距与磁感应强度成反比,线圈间距越小,线圈在中心区域产生的磁感应强度越大。
3.2. 平面线圈瞬态分析
在有限元仿真分析中,金属磨粒穿过三线圈油液磨粒传感器时,通过感应线圈得到感应电动势的变化情况;金属磨粒穿过平面线圈时,通过平面线圈得到磁场的变化。金属磨粒选用的材料为铁磁材料,其中相对磁导率为10,000,线圈选用的材料为铜材料,运动域和求解域的材料为系统默认的空气材料。
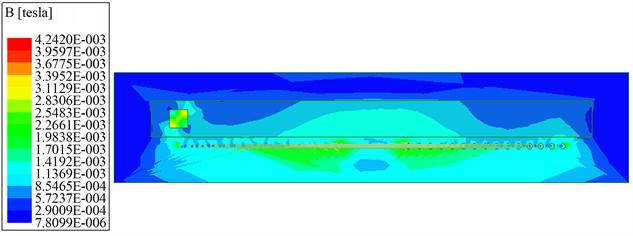
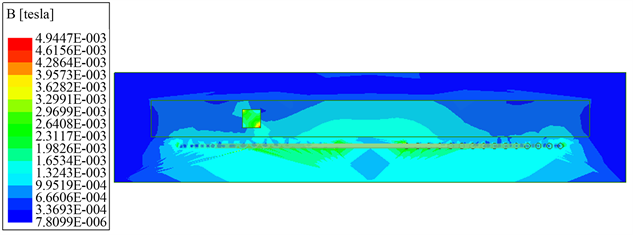
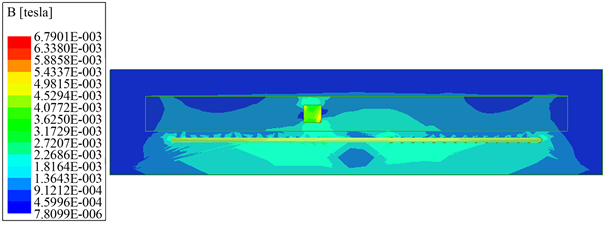
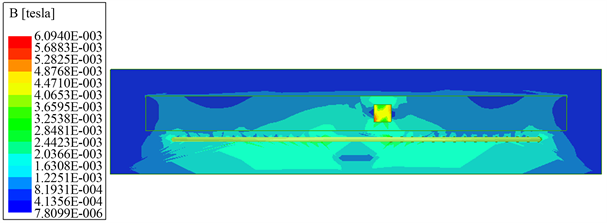
如图6(a)~(f)所示金属磨粒穿过平面线圈时在平面YOZ上的磁场分布云图。
图(a)为初始时刻平面线圈的磁场分布云图,图(b)为0.02 s时平面线圈的磁场分布云图,图(c)为0.04 s时平面线圈的磁场分布云图,图(d)为0.06 s时平面线圈的磁场分布云图,图(e)为0.08 s时平面线圈的磁场分布云图,图(f)为0.1 s时平面线圈的磁场分布云图。铁磨粒穿过平面线圈时,由于中间磁场最密集,所以越靠近线圈中心,磁场强度变化越大。
4. 结束语
本文主要是应用ANSYS Maxwell软件对平面线圈油液磨粒传感器进行了建模与有限元分析,通过稳
 (a)
(a)
 (b)
(b)
 (c)
(c)
Figure 4. Magnetic field distribution of planar coil at different parameters in YOZ plane
图4. 不同参数下的平面线圈YOZ平面上的磁场分布图

Figure 5. Magnetic field distribution
图5. 磁场分布图
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
 (e)
(e)
 (f)
(f)
Figure 6. Metal wear through the planar coil in magnetic flux density nephogram YOZ plane
图6. 金属磨粒穿过平面线圈时在YOZ平面上的磁场云图
态分析了平面线圈在XOY平面和YOZ平面上磁场分布云图,以及不同参数下平面线圈的磁场曲线图,由于每个线圈都施加了一个独立的电流源,所以每个线圈都能产生独立的磁场,相邻的线圈产生的磁场会部分抵消,所以曲线图为锯齿型,当激励源和匝数相同的情况下,线圈间距与磁感应强度成反比,线圈间距越小,线圈在中心区域产生的磁感应强度越大。通过瞬态分析了当金属磨粒穿过平面线圈时,YOZ平面上的磁场变化云图,铁磨粒穿过平面线圈时,越靠近线圈中心,磁场强度变化越大。本文主要对平面线圈油液磨粒传感器进行了理论研究和有限元分析,为传感器的参数优化提供了一定的理论基础。
致谢
本论文得到国家自然科学基金项目(51475098,61463010),广西自然科学杰出青年基金项目(2016GXNSFFA380008)以及广西高校海外“百人计划”、“卓越学者”计划等资助。
文章引用
仲昕杰,王衍学. 平面线圈油液磨粒传感器仿真研究
Study on the Simulation of Planar Coil Oil Grinding Sensor[J]. 传感器技术与应用, 2018, 06(02): 58-67. https://doi.org/10.12677/JSTA.2018.62007
参考文献
- 1. Wu, C., Zheng, C. and Ma, B. (2011) Simulation Study on the Characteristic of Ferromagnetic Wear Debris in Inductive Wear Debris Sensor. Chinese Journal of Scientific Instrument, 32, 2774-2780.
- 2. 谢友柏. 摩擦学面临的挑战及对策[J]. 中国机械工程, 1995(1): 6-9.
- 3. 万耀青, 马彪. 滚动轴承的损伤机理与大颗粒磨损金属的状态监测[J]. 机械强度, 2000, 22(3): 161-193.
- 4. 王衍学. 机械故障监测诊断的若干新方法及其应用研究[D]: [博士学位论文]. 西安: 西安交通大学, 2009.
- 5. Ding, Y., Wang, Y. and Xiang, J. (2016) An Online Debris Sensor System with Vibration Resistance for Lubrication Analysis. Review of Scientific Instruments, 87, 025109. https://doi.org/10.1063/1.4941440
- 6. Li, B., Yang, D., Hu, Z., et al. (2013) Theoretic Modeling and Numerical Simulation of the Electromagnetic Sensor for Online Wear Debris Monitoring. IEEE 2013 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), 15-18 July 2013, Chengdu, 1781-1784. https://doi.org/10.1109/QR2MSE.2013.6625922
- 7. 范红波, 张英堂, 陶凤和. 铁磁质磨粒形态对电感式磨粒传感器输出特性的影响[J]. 传感技术学报, 2009, 22(10): 1402-1405.
- 8. 张永祥, 明廷锋, 朴甲哲. 超声磨粒监测传感器设计研究[J]. 海军工程大学学报, 2002, 14(4): 28-31
- 9. 殷勇辉. 光纤油液污染监测传感器设计[J]. 仪表技术与传感器, 2006(11): 3-4.
- 10. 卞利, 李新星, 左洪福. 静电传感器在油液在线监测系统中的应用[J]. 润滑与密封, 2010, 35(3): 96-100.
- 11. Du, L. and Zhe, J. (2011) A High Throughput Inductive Pulse Sensor for Online Oil Debris Monitoring. Tribology International, 44, 175-179. https://doi.org/10.1016/j.triboint.2010.10.022
- 12. 于战果, 王宝光, 王海山. 应用探针式电容传感器检测发动机润滑油品质的研究[J]. 润滑与密封, 2007, 32(2): 171-173.