Journal of Sensor Technology and Application
Vol.
07
No.
02
(
2019
), Article ID:
29744
,
11
pages
10.12677/JSTA.2019.72005
Analysis of Zero Temperature Compensation of Resistance Strain Sensor
Zhipeng Yan
Zhonghang Electronic Measuring Instruments Co., Ltd., Hanzhong Shaanxi

Received: Mar. 26th, 2019; accepted: Apr. 10th, 2019; published: Apr. 17th, 2019

ABSTRACT
Zero temperature output is the main performance parameter of the strain sensor. If it is not controlled and compensated, the sensor accuracy is difficult to achieve 0.02% F.S per 10˚C. The main influencing factors of the zero temperature output of the sensor are defined, and the circuit compensation method and algorithm software compensation method are proposed. Through the compensation method, the sensor precision can be up to 0.02% F.S/10˚C, and the algorithm software compensation method can obtain higher precision.
Keywords:Strain Sensor, The Zero Temperature Output, Compensation, Circuit, Algorithm, Precision
电阻应变式传感器零点温度补偿剖析
晏志鹏
中航电测仪器股份有限公司,陕西 汉中

收稿日期:2019年3月26日;录用日期:2019年4月10日;发布日期:2019年4月17日

摘 要
零点温度输出是影响应变式传感器精度的主要性能指标,如果不加控制和补偿,很难达到0.02%FS/10℃的精度要求。明确传感器零点温度输出的主要影响因素,提出电路补偿法和算法软件补偿法。通过电路补偿法和算法软件补偿,可以将传感器精度提升至0.02%F.S/10℃,且算法软件补偿可获得更高精度。
关键词 :应变式传感器,零点温度输出,补偿,电路,算法,精度

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
电阻应变式传感器(以下简称传感器)采用电阻应变计作为敏感元件,用于力、质量、重心、位移等多物理量的测量和感知。实际应用中多采用惠斯通电桥组成全桥电路,将物理量转换成电信号,显示或表征物理量的大小,或用于过程控制和检测。当传感器不施加或感受任何物理量时,自由状态输出被称为零点输出,当环境温度发生变化时,零点输出会随之变化,这就是零点稳定度变化。如果不加控制和补偿,将会对传感器带来较大的影响,很难达到0.02%FS/10℃的精度要求 [1] 。
本文从传感器的温度零点产生的因素、机理进行了分析,对零点温度补偿原理进行了讨论,对零点温度补偿方法进行了探讨。
2. 影响传感器零点温度输出因素分析
在传感器的实际制作中均会采用温度自补偿应变计组成惠斯通全桥电路。由于敏感栅材料自身不均匀性和工艺差异,温度自补偿应变计的热输出系数会控制在 ≤ 1μm/m/℃,但在一个批次、不同应变计之间会存在分散,弹性体不同位置的线膨胀系数也会存在微小差异,当应变计粘贴到对应补偿材料的传感器弹性体上,同一桥路中的应变计输出(电阻变化)就会存在差异和分散。
根据应变计原理可知
(1)
式中ΔR/R为应变计电阻相对变化量;K为灵敏系数;ε为应变量,单位μm/m。
据应变计温度自补偿原理可知
(2)
式中εt为应变计热输出,单位μm/m;K为应变计灵敏系数;αt为应变计敏感栅电阻温度系数,单位10−6/℃;βs为弹性体材料线膨胀系数,单位10−6/℃;βg为敏感栅材料线膨胀系数,单位10−6/℃;Δt为温度变化量,单位℃。
当温度发生变化,应变计的输出就会发生变化,对应的电阻也就会发生变化。
即将式(1)和(2)结合
(3)
热输出系数为
(4)
式中Ct为热输出系数。
理论上,当完全温度自补偿时,热输出为0,即εt = 0,但实际上会存在一定的范围−1~1 μm/m/℃,极限状态下最大和最小之间相差2 μm/m/℃。
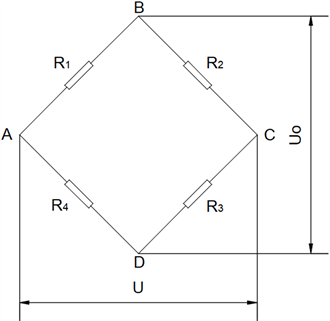
Figure 1. Diagram of Wheatstone full bridge circuit for strain gage
图1. 应变计惠斯通全桥电路
对于图1惠斯通电桥,当温度变化Δt时,其桥路输出为:
(5)
式中,R1、R2、R3、R4分别为桥臂应变计电阻,单位Ω;ΔR1、ΔR2、ΔR3、ΔR4分别为桥臂应变计电阻变化量,单位Ω;Uo为桥路输出,单位mV;U为供桥电压,单位V。
当 时,式(5)可简化为
(6)
由于ΔR1 + ΔR2,ΔR3 + ΔR4均远小于2R,分母可简化为2R,式(6)进一步简化为
(7)
分式上下同除以R,则
(8)
式中,εt2、εt3为桥臂应变计2和应变计3的热输出,单位μm/m。
假设灵敏系数K = 2,代入式(4)、式(8),可演化为
(9)
在制作传感器时,极限状态下,Ct2 − Ct3 = 2 μm/m/℃,当Δt = 50℃,则桥路相对输出最大为
(10)
当然,如果热输出系数控制较差一些,温度下的相对零点输出会更大。
实际应用中,连接桥路中应变计的导线长度和电阻也会存在差异,多数情况下,连接线为漆包线、绝缘镀锡铜线或绝缘镀银铜线等。虽然连线电阻很小,大约在1 Ω以内,但铜线电阻温度系数高达4000 ppm/℃,当环境温度发生变化,其电阻变化相对较大,桥路连接导线之间的电阻差异,也会带来相应的零点温度漂移,其计算方法基本与前述一致,不再赘述。
3. 传感器零点温度输出电路补偿法
为了减少传感器的零点温度输出,提高传感器精度,需要对传感器的零点温度输出进行补偿。通常情况下,根据零点温度输出的正负,选择在对应桥臂串联零点温度补偿电阻,增加温度下的电阻,使温度零点输出平衡。
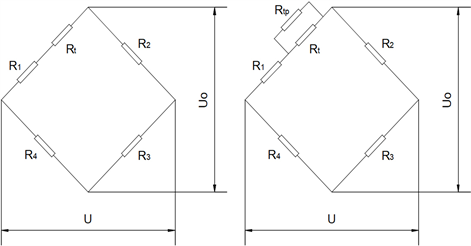 (a) 通用补偿法 (b) 并联电阻补偿法
(a) 通用补偿法 (b) 并联电阻补偿法
Figure 2. Diagram of zero temperature drift compensation circuit
图2. 零点温度漂移补偿电路示意图
对于图2(a)通用补偿法,温度零点补偿电阻Rt计算推导如下,通常桥路输出为:
(11)
当 ,并将温度零点补偿电阻Rt串入桥臂电阻R1中,则
(12)
式中ΔUo为温度下的桥路零载荷输出变化,单位mV;Uot为温度下零载荷桥路输出,单位mV;Uo为常温下零载荷桥路输出,单位mV;Rt为温度零点补偿电阻,单位Ω。
由于2ΔUo远小于激励电压U,可忽略不计,则
(13)
又 (14)
式中α为零点温度补偿电阻Rt的电阻温度系数;Δt为温差范围。
将式(14)代入式(12)
(15)
通常情况下,零点温度补偿电阻Rt采用ϕ0.1~ϕ0.15纯铜漆包线或纯镍漆包线绕制而成,在截面直径确定情况下只需要确定补偿丝的长度即可。以ϕ0.15纯铜漆包线为例,其电阻率位0.0172 mΩ·mm,电阻温度系数为0.004/℃,零点温度输出150 μV,桥路电阻350 Ω,桥路电压5 V,温差范围50℃,则
(16)
式中L为漆包铜线长度,单位mm;S为截面面积,单位mm2;ρ为电阻率,单位mΩ·mm。
理论计算的Rt电阻值,需要进行修正,在上述基础上乘以修正系数C,获得更高精度零点温度补偿要求。
对于图2(b)的并联电阻补偿法,可以获得更高的精度,一般情况下,Rt为固定阻值的铜电阻或镍电阻,阻值约为0.5~1 Ω任意固定值,通过调整并联精密电阻Rtp的阻值来调整零点温度补偿电阻 [2] 。严格意义上的补偿电路示意图见图3。
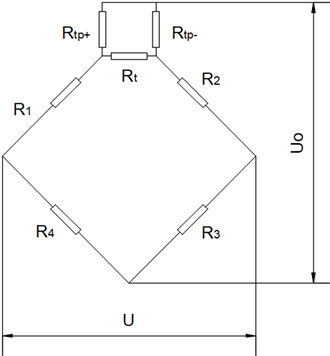
Figure 3. Actual circuit diagram of zero temperature compensation
图3. 零点温度补偿实际电路示意图
实际应用中,应用纯铜漆包线或纯镍漆包线时应对其进行稳定化处理,以提升补偿后的零点稳定性;而对于铜电阻或镍电阻,一般采用箔材蚀刻而成,会经过相应的处理,相对稳定性较高。
值得注意的是,由于零点温度补偿电阻大多数处于单一桥臂,相当于1/4桥,它对温度零点补偿输出会带来一定的非线性 [3] ,在实际应用中应适当考虑,而图3的电路补偿方法会降低非线性。
4. 传感器零点温度输出算法补偿
理论上来讲,零点温度输出是线性输出 [4] ,设初始零位为Uo,温度系数为γ,则零点输出为
(17)
补偿的方案是将一个随温度变化的信号叠加给温度零点输出,抵消a0Δt对传感器输出的影响,这个随温度变化信号可以由一个温度传感器获得。设温度传感器测得的信号为
(18)
式中β为温度传感器补偿系数。
零点温度补偿功能的传感器输入的输出简图为图4,具有可调系数λ,可以调整传感器的温度零点输出,其输出为
(19)
式(19)是传感器零点温度输出补偿的数学模型。
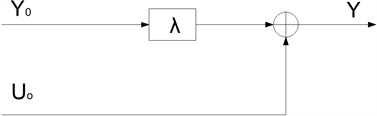
Figure 4. Diagram of zero temperature compensation sensor model
图4. 零点温度补偿传感器模型示意图
根据线性数学模型,可以采用曲线拟合,最小二乘法、神经网络等算法进行零点温度补偿。不管哪种算法,必须首先设置相应的温度传感器对传感器的表面温度进行采集,作为变量,对应跟随变量修正传感器输出,使应变传感器温度零点输出为零或接近于零,一般情况下均采用铂电阻作为测温传感器。
对于增加铂电阻未补偿的传感器,首先对温度传感器进行标定,形成一组数据,然后在温度变化的环境条件下对传感器的零点进行测试形成一组数据,随后对数据进行标定对应,形成标准曲线,对曲线进行拟合,获得不同的高次项系数,最优用软件算式对曲线拟合,测试输出,再修正高次项系数,获得最佳补偿结果。
分别用ZEMIC公司的BKM2350-3AA(23)T0-C应变计和德国H公司的3/350LT LA13 O应变计各制作8只20 Kg铝双孔平行梁传感器,在传感器中双孔中心外表面粘贴100 Ω铂电阻测温,放置在环境试验箱中,校准铂电阻温度,进行升降温,测试传感器在不同温度下的零点变化,得到相应的零点温度输出曲线图,详见图5和图6。

Figure 5. Zero output curve of the sensor without temperature compensation Which using ZEMIC strain gages
图5. ZEMIC应变计制作传感器未补偿温度零点输出曲线
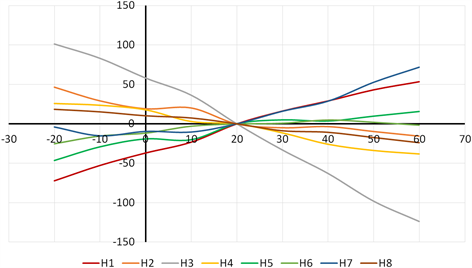
Figure 6. Zero output curve of the sensor without temperature compensation Which using H company strain gages
图6. H公司应变计制作传感器未补偿温度零点输出曲线
先对ZEMIC和H公司应变计制作的传感器平均温度零点输出曲线进行拟合。可以采用一元多项式拟合,一般情况下,单一曲线可以用式(20)表示。
(20)
式中Uot为温度t下的输出;t为标定后的铂电阻温度;a0~an为多项式系数。
可以采用线性代数计算,以温度t为变量,则式(20)可演化为不同一元高次方程式,即
(21)
根据韦达定理,可得
(22)
为了降低验算难度和程序的复杂度,一般最多选择5次项进行拟合。针对于ZEMIC应变计和H公司应变计制作的传感器测试数据,各抽取其中4只传感器对典型曲线进行拟合得到的拟合方程式。
编号ZEMIC1、ZEMIC5、ZEMIC6、ZEMIC8、H1、H3、H4、H7的传感器拟合结果为:
5. 传感器零点温度输出补偿结果验证
分别采用电路补偿和算法软件补偿方法进行了制作双孔平行梁传感器验证,具体结果如下。
5.1. 电路补偿验证
随机抽取10只未做补偿传感器测试高温、低温数据,初试结果见表1。
Table 1. List of uncompensated sensor test data
表1. 未补偿传感器测试数据列表
采用ϕ0.15纯铜漆包线进行补偿,其电阻率位0.0172 mΩ·mm,电阻温度系数为0.004/℃,对上表数据用式(15)、式(16)进行计算,得出每只传感器需要补偿的零点温度补偿电阻值和补偿漆包线的线长,根据修正补偿系数C修正,将漆包线补偿进桥路,进行高低温测试,结果过如表2。
Table 2. Sensor test results after compensation
表2. 补偿后的传感器测试结果
经过核算和系数计算后,90%传感器零点温度补偿后ZTC精度可以达到0.02%以内。
5.2. 算法软件补偿验证
为了能够准确反应传感器的零点在温度下的变化,特意对ZEMIC型号BKM2350-3AA(23)T0-C应变计和H公司3/350LT LA13 O应变计的热输出进行了测试,结果如图7。
 (a) ZEMIC应变计样品热输出曲线
(a) ZEMIC应变计样品热输出曲线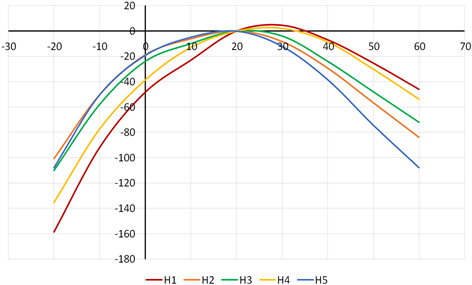 (b) H公司应变计样品热输出曲线
(b) H公司应变计样品热输出曲线
Figure 7. The thermal output test curves of ZEMIC and H company strain gages
图7. ZEMIC和H公司应变计热输出测试曲线
从曲线来看,ZEMIC和H公司应变计热输出曲线趋势基本一致,ZEMIC负温段热输出相较H公司偏正,正温段热输出相较H公司偏负,因此制作传感器的ZTC (Zero Temperature Compensation,零点温度补偿)性能应基本一致。图5和图6的曲线结果也验证了前述推断。
根据前述曲线拟合获得的拟合公式和参数对传感器的输出进行算法程序拟合,分别对采用ZEMIC和H公司应变计的铝传感器进行曲线拟合,拟合后的对比曲线详见图8。
根据拟合曲线和系数,编写ZTC补偿拟合算法程序,注入芯片后进行测试,结果拟合补偿后的传感器性能全部达到了0.02%F.S/10℃,甚至90%达到了0.015%F.S/10℃以内,相比电路补偿可以得到更高的精度,且在全温范围内有较好的线性。
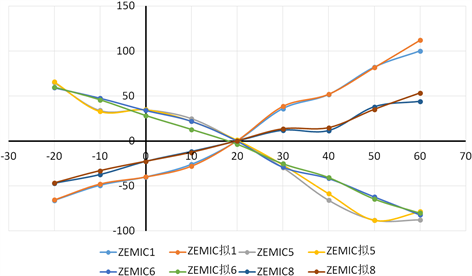 (a) ZEMIC应变计制作传感器ZTC拟合曲线
(a) ZEMIC应变计制作传感器ZTC拟合曲线 (b) H公司应变计制作传感器ZTC拟合曲线
(b) H公司应变计制作传感器ZTC拟合曲线
Figure 8. ZTC fitting curve of aluminum sensors were made by different strain gages
图8. 不同应变计制作铝传感器ZTC拟合曲线
目前电路补偿方法已经大批量应用于应变式传感器补偿工序,取得了良好的效果,批量补偿C3级传感器一次合格率可以达到95%以上。曲线拟合和软件修正方法也已经成功应用于数字补偿传感器和智能传感器,正在进行批量推广和应用。
6. 结论
通过理论分析,明确应变式传感器零点温度输出的主要影响因素和来源。推导了温度零点电路补偿的理论公式,对电路补偿法进行了介绍和实际验证。明确了算法补偿的主要依据是曲线拟合,也对相应方法和实际应用情况进行了介绍。
结果表明,通过电路补偿法和算法软件补偿,均可以将应变式传感器的ZTC性能提升至0.02%F.S/10℃以内。软件算法补偿相比电路补偿可以获得更高的精度,在全温范围内有较好的线性。
文章引用
晏志鹏. 电阻应变式传感器零点温度补偿剖析
Analysis of Zero Temperature Compensation of Resistance Strain Sensor[J]. 传感器技术与应用, 2019, 07(02): 39-49. https://doi.org/10.12677/JSTA.2019.72005
参考文献
- 1. 刘九卿. 称重传感器电路补偿机理及补偿电阻计算[J]. 衡器, 2014, 43(1): 23-29.
- 2. Zandman, F., Simon, P.-R. and Szwarc, J. (2002) Resistor Theory and Technology. Published by SciTech Publishing Inc., USA.
- 3. Vishay Strain Gages and Instruments Document Number: 11054, Strain Gage Thermal Output and Gage Factor Variation with Temperature. USA: Published by Instruments Division, 14 August 2014.
- 4. 刘诗斌, 高德远, 李树国. 传感器温度补偿的调试规律研究[J]. 化工自动化及仪表, 2000, 27(1): 51-53.
