Creative Education Studies
Vol.
10
No.
05
(
2022
), Article ID:
51166
,
7
pages
10.12677/CES.2022.105146
高中数学化归思想培养探究
历德珍,史卫娟*
湖南人文科技学院数学与金融学院,湖南 娄底
收稿日期:2022年3月18日;录用日期:2022年5月4日;发布日期:2022年5月11日

摘要
数学化归思想是高中数学中一种重要思想,其对学生解题能力与数学素养的培养起着不可忽视的作用。为积极响应国家新课改的相关要求,提高教师授学生以“渔”的意识,文章通过分析化归思想的基本内涵,结合实例探究化归思想方法在高中学习中的应用,如特殊与一般、常量与变量、函数与方程等,总结归纳新时代数学教师如何在课堂上正确渗透化归思想进行论述。教师通过指导学生体会转化和归结过程的重要性,感受化归思想方法形成的过程,让学生在解题活动中训练数学化归思维,从而锻炼学生的数学逻辑思维,提高数学素养。
关键词
化归思想,高中数学,转化

An Exploration on the Mathematics Conversion and Concatenation in Senior High School
Dezhen Li, Weijuan Shi*
School of Mathematics and Finance, Hunan University of Humanities, Science and Technology, Loudi Hunan
Received: Mar. 18th, 2022; accepted: May 4th, 2022; published: May 11th, 2022

ABSTRACT
Mathematics conversion and concatenation is an important thinking in high school mathematics, which has an irreversible role in the cultivation of student solving ability and mathematics literacy. In order to actively respond to the relevant requirements of the national new curriculum reform, improve teachers’ awareness of teaching students to fish. This article summarizes how the new era math teachers to infiltrate the thought of mathematics conversion and concatenation in class correctly. This paper also researches the application of mathematics conversion and concatenation by combining instance like special and general, constants and variables, functions and equations, etc. in high school math class to analyses of the basic connotation of the idea. By guiding students to appreciate the importance of the process of transformation and induction and to feel the process of forming the idea of Mathematics conversion and concatenation, teachers allow students to train Mathematical transformation and inductive thinking in problem solving activities, so as to exercise students’ mathematical logical thinking and improve mathematical literacy.
Keywords:Mathematics Conversion and Concatenation, High School Mathematics, Transformation

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
化归思想就如同翻译,将同一个问题用不同的表达形式在不同的思想水平上表现出来,以便于寻找解决问题的突破口。简单地理解,就是将一个难以解决的问题,转化为已经解决或者通过某种方式容易解决的一类问题,最终使原问题迎刃而解。
利用化归思想解决问题的一般过程见图1:
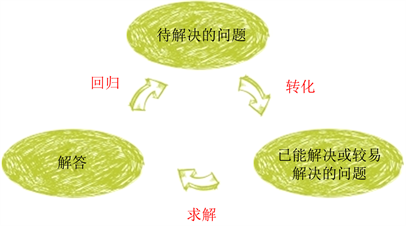
Figure 1. General process for problem solving
图1. 解决问题的一般过程
“化归”即转化与归结的意思,刘海涛 [1] 在《高中数学解题中转化思想的应用研究》中指出,高中数学题万变不离其宗,只要找到转化的点,掌握基本的解题技能,完成知识与方法的迁移,就可以高效率找到切入点。赵芳 [2] 在《浅谈化归思想在高中数学教学中的应用》谈到,教师不仅要教会学生解决固定的数学题,还要将化归思想融入到解决问题的过程中去,正确引导学生进行自我数学知识体系的构建 [3],提高数学素养,为以后的数学学习奠定基础。王羚昱 [4] 在《化归思想在高中数学教学中的应用原则》提出,教师可以利用简化与直观原则,转化解题思路,简化过程,提升学生的解题技能。化归思想在高考中起着十分重要的作用,它几乎可以渗透到所有的数学内容和问题解决过程中。本文以具体例题论述在高中数学的学习中,数学化归思想的应用极其广泛,例如特殊与一般,命题与命题、常量与变量、函数方程以及不等式三者等,教师应根据问题特征,引导学生正确利用化归思想,运用已学知识解决陌生问题。
2. 化归思想方法在高中数学课堂教学中的应用
在日常解题中,不可避免会遇到超出复习知识范围的问题,化归思想作为“武器”,可以帮助学生完美解决问题。大部分学生现阶段的数学知识体系相对薄弱,而作为新时代人民教师,除了讲授书本上的基础知识外,还需加强对数学化归思想的训练,锻炼学生数学推理能力,培养学生解题的能力,为学生未来的数学学习和生活打下了坚实基础。当前广大数学教师在课堂上运用到的数学化归思想主要有特殊与一般转化思想、等价转化思想、常量与变量的转化思想以及函数方程不等式三者之间的相互转化思想等。
2.1. 特殊与一般的转化
如果一个问题难以着手,通过观察和分析特例,找到问题的特殊数量或关系,然后扩展到一般情况,从特例到一般情况的过渡,这就是特殊化的化归策略 [5]。在解决一个问题时,可能需要将一般问题归类为特殊问题,或者将特殊问题归类为一般问题。这需要教师在平时讲解题目时做好归纳总结,帮助学生学以致用。
例1、(2019,成都) ,, (其中e为自然常数)的大小关系是( )。
A. B. C. D.
分析:若是用 计算量比较大,观察三个数,易发现它们的结构属性,构造函数 ,将问题转化为求函数值 ,, 的大小。
解:因为 ,,,
所以令 ,
因为 ,
所以 在 单调递增,
所以 ,
所以 。
此题选A。
思维升华:由三个具体值的比较,根据特征,抽象出一个一般函数,对一般函数的单调性进行研究,得到这三个特殊数的大小关系,这是特殊与一般的转化方法。
2.2. 命题的等价转化
等价转换要求转换过程中有充分必要的因果关系,确保转化的结果总是解决原始问题的结果。实际上我们在转化的时候方法往往有很多,一般情况下,有几种转化方法就有可能得出几种解题方案,这也是我们在解题的时需多加推敲的一些环节。教师可以引导学生从多方面多角度对原题目进行提炼,选择合适的解题思路。
例2、(2016,洛阳)若函数 的图像关于直线 对称,则 的最大值为。
解析:法一:含有未知数的函数表达式,先求出未知数,接着利用单调性可以得到最大值,但是这种方法需要大量的计算。法二:利用换元法,将高阶函数转化为二次函数,并求最值。
解:因为函数图象关于直线 对称,
所以 ,,
所以 是方程 的根,
所以根据韦达定理 ,
解得 ,。
(法一)所以 ,
由 ,
得 ,,,
易知 在 内为增函数,在 内为减函数,在 内为增函数,在 为减函数,
所以
,
求得 的最大值为16。
(法二)
,
令 ,则 ,
因为函数开口向下,当 时, 。
思维升华:通过因式分解发现 这样的特征,利用换元,从而将高次函数转化为我们所熟悉的二次函数。化归思想方法有助于我们使用不同的方法解决问题,实现不同的角度变换,连接多个知识点,提高发散思维能力。
2.3. 常量与变量的转化
在处理多变量问题时,给定了常量(或参数)的取值范围,求变量x的范围时,往往会进行常、变量之间的转化。
例3、(2017,河南)已知函数 , 其中 是 的导函数。对满足 的一切a的值,都有 ,则实数x的取值范围为。
分析:从习惯性的把x当作变量,结合问题是 恒成立,选择将a作为变量,写出关于a的函数式子,结合直线的图像特征,使得在直线两端点处的值小于0,求解不等式组即可。
解:由题可知 ,
则 对 恒成立。
令 ,
则 ,
所以实数x的取值范围为 。
思维升华:由于题目中是对 进行任意取值,就不能习惯性地将x作为变量来处理,反而要将x当作参数a作为变量,体现了常量语变量的转化。
2.4. 函数、方程与不等式之间的转化
函数、方程与不等式三者之间可以相互转化 [6],要解决方程和不等式的问题,需要函数的帮助;而要解决函数的问题,需要方程和不等式的帮助。为了便于找到问题思路,常将不等式恒成立问题转化为函数最值问题;将不等式问题转化为函数单调性和最值问题;将微分方程的解问题转化为函数的零点问题、函数图象的交点问题等 [7]。
例4、(2020,重庆)关于x的不等式 对 恒成立,则实数a的取值范围。
分析:面对恒成立问题,优先套路进行参变量分离,将恒成立问题转化为最值问题,利用基本不等式,求出最小值,这里要注意满足基本不等式的条件是否存在。
解:由题可知 恒成立,
即 。
令 (当且仅当 ,即 ),
所以 ,
所以实数a的取值范围为 。
思维升华:恒成立问题在高中数学中是最常见的一种题型,一般解题思路有两种,一种先进行参变分离,再转化为最值问题;另一种是直接含参,将其转化为最值问题,借助对参数的分类讨论来研究。
3. 培养化归思想,提升学生的数学素质
在高中数学中,将陌生的数学题熟悉化,复杂问题简单化,抽象问题具体化,运用之前学习的内容,展开联想,让旧知识通过新方法解决新问题,数学思维方向会得到拓宽,在遇到陌生复杂问题时就不会出现“脑袋空空”,不知从何下手的现象。
3.1. 化陌生为熟悉,遵循熟悉化原则
化归思想的运用基于学生自身的知识基础,教师一方面加强学生对现阶段高中应掌握的数学知识的理解;另一方面,要做好引导工作,指导学生在遇到陌生题目时,如何建立新旧知识之间的联系,由陌生化熟悉,寻找合适的解题方法。
例5、(2021,衡水五校联考)已知集合 ,,则 ( )。
A. B. C. D.
解:由 得 ,,
又因为 ,
所以 。
故选:C。
思维升华:直接求解集合解集很困难,学生基于教师的引导回忆,将题目转化为一元二次不等式的求解问题,从而得到问题的解。教师要充分把握题目内涵,虽然数学题目变幻莫测,其本质并没有发生变化。
3.2. 化繁为简,遵循简单化原则
当遇到问题比较复杂笼统,为了降低题目的抽象程度,通过转化为低维少元去解决。例如在例2中利用换元法降低函数的次数,简化了运算过程。
有时遇到从正面直接分析所给式子和图形结构较难较繁,不妨将想法“绕道而行”,转向问题的结论或者相反的条件,迂回地得到解题思路。在课堂上,教师为学生理顺解题步骤,渗透化归思想方法,设计符合学生思维意识的问题,完美契合学生的身心发展规律。
3.3. 化抽象为具体,遵循直观化原则
数学有思维逻辑严谨、知识点抽象的特点。而抽象问题的具体化是一种常见的解题思路。它是对抽象问题的进一步理解与认识,在抽象语言与具体问题之间创建关联,以实现抽象向具体的转化归结。
例6、(2021,安徽江淮)已知正实数a,b,c满足 ,,,则( )。
A. B. C. D.
解:在同一直角坐标系中画出函数 ,,, 的图象,
如图2所示a,b,c分别为两个函数图象交点的横坐标,
根据图象可知 。
故选A。
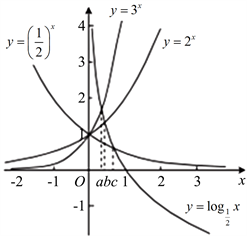
Figure 2. Three image intersections
图2. 三个图像交点情况图示
思维升华:在理解问题过程中,常常需要把比较抽象的问题转化为比较直观、具体的问题。也可以适当引用生活中的实际经验,使问题易于理解,降低题目难度。
4. 总结
熟悉和牢牢掌握基本知识、基本技能、基本方法是化归的基础;丰富的联想、仔细的观察和类比是实现化归的手段。高中生已经具备一定程度上的举一反三能力,而且思维更加活跃,喜欢创新和表达,教师需遵循高中生的心理发展规律,由简到难,由表及里,避免出现高估学生能力的现象。教师要对学生进行正确引导,深度挖掘教材内容,使学生对定理和公式有深刻的理解,达到可以自主归纳和提炼典型题目。同时鼓励学生思维发散,积极主动去发现事物之间的本质联系,帮助学生掌握化归思想,营造积极热情的学习气氛,促进了数学教学质量的提高。
随着科学技术的不断发展,教师需要具有时代特色,将信息技术融入到基本方法的渗透中,以提高教育效果。例如,借助多媒体应用和化归思想的结合,学生可以直观、立体地体验绘制平面空间图像的过程,提高学生对相应理论的理解。教师可以根据学生的数学实力将全班分成多组,保证每组的综合实力一致。然后让每个小组讨论题目多解,自主探寻,可在一旁做相应指导,有序培养学生的转化结合能力。重视转化与归结过程,培养数学化归思想是学好高中数学的敲门砖。
基金项目
本论文由2021年湖南人文科技学院教育教学改革项目《数学与应用数学专业教育见习过程考核研究与实践》(项目编号:RKJGY2109)支持。
文章引用
历德珍,史卫娟. 高中数学化归思想培养探究
An Exploration on the Mathematics Conversion and Concatenation in Senior High School[J]. 创新教育研究, 2022, 10(05): 903-909. https://doi.org/10.12677/CES.2022.105146
参考文献
- 1. 刘海涛. 高中数学解题中转化思想的应用研究[J]. 数理化解题研究, 2020(10): 7-8.
- 2. 赵芳. 浅谈化归思想在高中数学教学中的应用[J]. 试题与研究, 2022(1): 28-29.
- 3. 何惠萍. 化归思想在高中数学解题过程中的应用[J]. 高考, 2020(14): 33.
- 4. 王羚昱. 化归思想在高中数学教学中的应用原则[J]. 语数外学习(高中版中旬), 2019(3): 45.
- 5. 蒋明祥. 数学化归思想方法的教学策略解析[J]. 高考, 2019(22): 111.
- 6. 高玉萍. “化归思想”让数学学习变得轻松有效——中学数学化归思想方法的教学策略[J]. 高考, 2019(25): 35.
- 7. 邱进. 浅谈高中数学解题技巧[J]. 数理化解题研究, 2021(18): 27-28.
NOTES
*通讯作者。