带形状参数的四次DP曲线的构造与应用 Construction and Application of the Quartic DP Curve with Shape Parameters

doi:10.12677/AAM.2021.1010378

Advances in Applied Mathematics
Vol. 10 No. 10 ( 2021 ), Article ID: 46058 , 10 pages
10.12677/AAM.2021.1010378

带形状参数的四次DP曲线的构造与应用

王研，宋九锡，秦凌云，沈洋，彭兴璇

●How to Cite this Article

辽宁师范大学数学学院，辽宁大连

收稿日期：2021年9月25日；录用日期：2021年10月18日；发布日期：2021年10月27日

摘要

本文将四次DP基函数进行推广，构造出带形状参数的四次DP基函数，分析了带形状参数的四次DP基函数的性质。然后基于这组基函数定义了带形状参数的四次DP曲线，讨论了形状参数的几何意义。最后利用最小二乘法将端点插值的带形状参数的四次DP曲线进行圆锥曲线逼近，求出带形状参数的四次DP曲线的控制顶点，并展示了实例。

关键词

四次DP曲线，形状参数，圆锥曲线，逼近

Construction and Application of the Quartic DP Curve with Shape Parameters

Yan Wang, Jiuxi Song, Lingyun Qin, Yang Shen, Xingxuan Peng

School of Mathematics, Liaoning Normal University, Dalian Liaoning

Received: Sep. 25^th, 2021; accepted: Oct. 18^th, 2021; published: Oct. 27^th, 2021

ABSTRACT

In this paper, the quartic DP basis functions are extended, the quartic DP basis functions with shape parameters are constructed, the properties of the quartic DP basis functions with shape parameters are analyzed. Then, based on the basis functions, the quartic DP curve with shape parameters is defined, the geometrical meanings of the shape parameters are discussed. Finally, we use the least squares method and approximate conic sections by the quartic DP curve with shape parameters with endpoint interpolation, find the control points of the quartic DP curve with shape parameters, and examples are shown.

Keywords:Quartic DP Curve, Shape Parameters, Conic Section, Approximation

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

自由曲线曲面的研究一直以来受到学者们的广泛关注，Delgado和Peña [1] 提出了一类新型参数曲线，称为DP曲线，该曲线具有端点插值性、数值计算稳定性、线性计算复杂度、曲线保形性等性质。为了解决DP曲线的形状调节问题，陈杰等 [2] 提出带多个形状参数的DP-NTP曲线，形状参数可以较好地进行外形调节；陈福来 [3] 结合形状参数和DP基提出了另一种形式的广义三次DP基及曲线，并讨论了曲线参数连续和几何连续的拼接条件；彭兴璇等 [4] 通过在端点处的切矢引入形状参数，包括张力参数 $α$ 和偏移参数 $β$ ，构造了一类带形状参数的三次DP曲线；张迪等 [5] 将三次DP基函数的定义区间由 $[0, 1]$ 推广到 $[0, α]$ ，重新参数化构造了α-DP曲线。

在几何外形设计和机器制造中，圆锥曲线占有重要的地位，由于圆锥曲线(抛物线段除外)不能用多项式曲线精确表示，许多学者将注意力集中在多项式曲线逼近包括圆弧在内的圆锥曲线上，Floater [6] 给出了任意奇数阶的Bézier曲线对圆锥曲线的逼近，有最佳逼近阶 $2 n$ ；Ahn [7] 通过在端点处具有 $G^{1}$ 或 $G^{2}$ 连续性的四次Bézier曲线提供了圆锥曲线的两种逼近方法；胡倩倩 [8] 提出了一种任意阶的受约束的Bézier曲线逼近圆锥曲线的算法；Davood Bakhshesh [9] 提出了一种利用最小二乘法将端点插值的任意阶DP曲线进行圆锥曲线逼近的算法；张伟红等 [10] 人根据圆弧端点和端点切向量提出等弧长多项式逼近方法，给出了五次PH多项式逼近圆弧的精确表示。

在现有DP曲线及逼近算法基础上，本文构造了带形状参数的四次DP基函数，给出了带形状参数的四次DP曲线的定义和性质，明确了形状参数的几何意义，并在Davood Bakhshesh提出的算法基础上考虑带形状参数的四次DP曲线逼近圆锥曲线，改善了逼近曲线的灵活度，最后给出了数值例子。

2. 带形状参数的四次DP基函数

定义1对于 $t \in [0, 1]$ ， $0 \leq α, m, p, q, β \leq 1$ ，称关于 $t$ 的多项式

${\begin{array}{l} D_{0, 4} (t) = {(1 - t)}^{3} (1 - α t) \\ D_{1, 4} (t) = (1 - t) t (α {(1 - t)}^{2} + 3 (1 - m) (1 - p)) \\ D_{2, 4} (t) = 3 ((1 - m) p + m q) (1 - t) t \\ D_{3, 4} (t) = (1 - t) t (β t^{2} + 3 m (1 - q)) \\ D_{4, 4} (t) = t^{3} (1 - β (1 - t)) \end{array}$

为带形状参数的四次DP基函数；其中，参数 $α, m, p, q, β$ 为形状参数。

带形状参数的四次DP基函数具有如下性质：

1) 非负性，对 $t \in [0, 1]$ ， $0 \leq α, m, p, q, β \leq 1$ ，有 $D_{i, 4} (t) \geq 0, i = 0, 1, 2, 3, 4$ 。

2) 权性，对 $t \in [0, 1]$ ， $0 \leq α, m, p, q, β \leq 1$ ，有 $\sum_{i = 0}^{4} D_{i, 4} (t) = 1$ 。

3) 端点性质，即

$\begin{array}{l} D_{0, 4} (0) = 1, D_{1, 4} (0) = 0, D_{2, 4} (0) = 0, D_{3, 4} (0) = 0, D_{4, 4} (0) = 0; \\ D_{0, 4} (1) = 0, D_{1, 4} (1) = 0, D_{2, 4} (1) = 0, D_{3, 4} (1) = 0, D_{4, 4} (1) = 1; \\ {D^{'}}_{0, 4} (0) = - 3 - α, {D^{'}}_{1, 4} (0) = 3 (1 - m) (1 - p) + α, {D^{'}}_{2, 4} (0) = 3 ((1 - m) p + m q), \\ {D^{'}}_{3, 4} (0) = 3 m (1 - q), {D^{'}}_{4, 4} (0) = 0; \end{array}$

$\begin{array}{l} {D^{'}}_{0, 4} (1) = 0, {D^{'}}_{1, 4} (1) = - 3 (1 - m) (1 - p), {D^{'}}_{2, 4} (1) = - 3 ((1 - m) p + m q), \\ {D^{'}}_{3, 4} (1) = - 3 m (1 - q) - β, {D^{'}}_{4, 4} (1) = 3 + β . \end{array}$

4) 退化性，当 $α = β = 1$ 且 $(1 - m) (1 - p) = m (1 - q) = 0$ 时，带形状参数的四次DP基函数退化为四次DP基函数。

5) 最值性， $D_{i, 4} (t) \geq 0 (i = 0, 1, 2, 3, 4)$ 在 $[0, 1]$ 上均有一个最大值。

6) 拟对称性，当 $α = β$ 且 $(1 - m) (1 - p) = m (1 - q)$ 时， $D_{i, 4} (t) = D_{4 - i, 4} (t)$ $(i = 0, 1, 2, 3, 4)$ 。

3. 带形状参数的四次DP曲线及性质

定义2给定5个控制顶点 $b_{i} \in R^{d} (i = 0, 1, 2, 3, 4, d = 2, 3)$ ，称曲线：

$b (t) = \sum_{i = 0}^{4} b_{i} D_{i, 4} (t) (t \in [0, 1])$ (1)

为带形状参数的四次DP曲线，其中 $D_{i, 4} (t) (i = 0, 1, 2, 3, 4)$ 为带形状参数的四次DP基函数。

带形状参数的四次DP曲线具有如下性质：

1) 端点性质，即

$b (0) = b_{0}, b (1) = b_{4},$

${\begin{array}{l} \begin{matrix} b^{'} (0) = (3 + α) (b_{1} - b_{0}) + (3 - 3 (1 - m) (1 - p)) (b_{2} - b_{1}) \\ + 3 m (1 - q) (b_{3} - b_{2}), \end{matrix} \\ \begin{matrix} b^{'} (1) = 3 (1 - m) (1 - p) (b_{2} - b_{1}) + (3 - 3 m (1 - q)) (b_{3} - b_{2}) \\ + (3 + β) (b_{4} - b_{3}), \end{matrix} \end{array}$

${\begin{array}{l} \begin{matrix} b^{″} (0) = - 6 (1 + α) (b_{1} - b_{0}) + (- 6 + 6 (1 - m) (1 - p)) (b_{2} - b_{1}) \\ + (- 6 m (1 - q)) (b_{3} - b_{2}), \end{matrix} \\ \begin{matrix} b^{″} (1) = 6 (1 - m) (1 - p) (b_{2} - b_{1}) + (6 - 6 m (1 - q)) (b_{3} - b_{2}) \\ + (6 + 6 β) (b_{4} - b_{3}) . \end{matrix} \end{array}$

2) 拟对称性，当 $α = β$ 且 $(1 - m) (1 - p) = m (1 - q)$ 时，由控制多边形 $b_{0} b_{1} b_{2} b_{3} b_{4}$ 和 $b_{4} b_{3} b_{2} b_{1} b_{0}$ 生成的带形状参数的四次DP曲线相同，只是定向相反。

3) 凸包性，由带形状参数的四次DP基函数的非负性、权性知，曲线落在控制顶点生成的凸包内。

4) 几何不变性与仿射不变性，由带形状参数的四次DP基的规范性得到。

5) 退化性，当 $α = β = 1$ 且 $(1 - m) (1 - p) = m (1 - q) = 0$ 时，带形状参数的四次DP曲线退化为四次DP曲线。

4. 形状参数对曲线形状的影响

$\begin{matrix} b (t) = \sum_{i = 0}^{4} b_{i} D_{i, 4} (t) = (\begin{array}{l} b_{0} & b_{1} & b_{2} & b_{3} & b_{4} \end{array}) (\begin{array}{l} D_{0, 4} (t) \\ D_{1, 4} (t) \\ D_{2, 4} (t) \\ D_{3, 4} (t) \\ D_{4, 4} (t) \end{array}) \\ = (\begin{array}{l} b_{0} & b_{1} & b_{2} & b_{3} & b_{4} \end{array}) (\begin{array}{l} 1 & 1 - α & 0 & 0 & 0 \\ 0 & α & (1 - m) (1 - p) & 0 & 0 \\ 0 & 0 & (1 - m) p + m q & 0 & 0 \\ 0 & 0 & m (1 - q) & β & 0 \\ 0 & 0 & 0 & 1 - β & 1 \end{array}) (\begin{array}{l} {(1 - t)}^{4} \\ {(1 - t)}^{3} t \\ 3 (1 - t) t \\ (1 - t) t^{3} \\ t^{4} \end{array}) \\ = (\begin{array}{l} b_{0}^{*} & b_{1}^{*} & b_{2}^{*} & b_{3}^{*} & b_{4}^{*} \end{array}) (\begin{array}{l} {(1 - t)}^{4} \\ {(1 - t)}^{3} t \\ 3 (1 - t) t \\ (1 - t) t^{3} \\ t^{4} \end{array}) \\ = \sum_{i = 0}^{4} b_{i}^{*} e_{i}^{4} \end{matrix}$ (2)

其中， $e_{i}^{4} (i = 0, 1, 2, 3, 4)$ 为四次DP基函数， $b_{0}^{*} = b_{0}$ ， $b_{1}^{*} = (1 - α) b_{0} + α b_{1}$ ， $b_{2}^{*} = (1 - m) ((1 - p) b_{1} + p b_{2}) + m (q b_{2} + (1 - q) b_{3})$ ， $b_{3}^{*} = β b_{3} + (1 - β) b_{4}$ ， $b_{4}^{*} = b_{4}$ 。由式(2)知，带形状参数的四次DP曲线式(1)可看成以 $b_{0}^{*}, b_{1}^{*}, b_{2}^{*}, b_{3}^{*}, b_{4}^{*}$ 为控制顶点的四次DP曲线。

当修改形状参数 $α, β$ 的值时，相当于调整控制顶点 $b_{1}^{*}, b_{3}^{*}$ 的位置。 $α$ 由小变大时， $b_{1}^{*}$ 在 $b_{0} b_{1}$ 上向 $b_{1}$ 靠近， $β$ 由小变大时， $b_{3}^{*}$ 在 $b_{3} b_{4}$ 上向 $b_{3}$ 靠近。

当修改形状参数 $m, p, q$ 的值时，相当于调整控制顶点 $b_{2}^{*}$ 的位置。 $(1 - m) (1 - p)$ 、 $(1 - m) p + m q$ 、 $m (1 - q)$ 是点 $b_{2}^{*}$ 关于 $Δ b_{1} b_{2} b_{3}$ 的重心坐标，可以调节 $b_{2}^{*}$ 在 $Δ b_{1} b_{2} b_{3}$ 里取值，从而灵活地调控生成曲线的形状。

5. 带形状参数的四次DP曲线逼近圆锥曲线

5.1. 圆锥曲线的矩阵表示

圆锥曲线可用标准的二次有理Bézier曲线表示为

$C (t) = \frac{{(1 - t)}^{2} c_{0} + 2 ω t (1 - t) c_{1} + t^{2} c_{2}}{{(1 - t)}^{2} + 2 ω t (1 - t) + t^{2}} t \in [0, 1],$

其中， $c_{0}, c_{1}, c_{2}$ 是控制顶点。当 $0 < ω < 1$ 时， $C (t)$ 表示椭圆；当 $ω = 1$ 时， $C (t)$ 表示抛物线；当 $ω > 1$ 时， $C (t)$ 表示双曲线；当 $ω < 0$ 时， $C (t)$ 表示原来圆锥曲线段的剩余部分。

令 $r (t) = \frac{1}{{(1 - t)}^{2} + 2 ω t (1 - t) + t^{2}}$ ， $B_{2} = (\begin{matrix} {(1 - t)}^{2} & 2 t (1 - t) & t^{2} \end{matrix})$ ， $G = (\begin{matrix} 1 & 0 & 0 \\ 0 & ω & 0 \\ 0 & 0 & 1 \end{matrix})$ ， $c = (\begin{matrix} c_{0} \\ c_{1} \\ c_{2} \end{matrix})$ ，则有 $C (t) = r (t) \cdot B_{2} \cdot G \cdot c$ 。

5.2. 带形状参数的四次DP曲线的矩阵表示

将式(1)中带形状参数的四次DP曲线写成如下形式：

$\begin{matrix} b (t) = (\begin{array}{l} D_{0, 4} (t) & D_{1, 4} (t) & D_{2, 4} (t) & D_{3, 4} (t) & D_{4, 4} (t) \end{array}) (\begin{array}{l} b_{0} \\ b_{1} \\ b_{2} \\ \begin{array}{l} b_{3} \\ b_{4} \end{array} \end{array}) \\ = (\begin{array}{l} e_{0}^{4} & e_{1}^{4} & e_{2}^{4} & e_{3}^{4} & e_{4}^{4} \end{array}) (\begin{array}{l} 1 & 0 & 0 & 0 & 0 \\ 1 - α & α & 0 & 0 & 0 \\ 0 & (1 - m) (1 - p) & (1 - m) p + m q & m (1 - q) & 0 \\ 0 & 0 & 0 & β & 1 - β \\ 0 & 0 & 0 & 0 & 1 \end{array}) (\begin{array}{l} b_{0} \\ b_{1} \\ b_{2} \\ \begin{array}{l} b_{3} \\ b_{4} \end{array} \end{array}), \end{matrix}$

将上式改写为如下形式：

$T_{4} (t) (\begin{array}{l} 1 & 0 & 0 & 0 & 0 \\ - 4 & 1 & 3 & 0 & 0 \\ 6 & - 3 & - 3 & 0 & 0 \\ - 4 & 3 & 0 & 1 & 0 \\ 1 & - 1 & 0 & - 1 & 1 \end{array}) (\begin{array}{l} 1 & 0 & 0 & 0 & 0 \\ 1 - α & α & 0 & 0 & 0 \\ 0 & (1 - m) (1 - p) & (1 - m) p + m q & m (1 - q) & 0 \\ 0 & 0 & 0 & β & 1 - β \\ 0 & 0 & 0 & 0 & 1 \end{array}) (\begin{array}{l} b_{0} \\ b_{1} \\ b_{2} \\ \begin{array}{l} b_{3} \\ b_{4} \end{array} \end{array})$

即

$T_{4} (t) (\begin{array}{l} 1 & 0 & 0 & 0 & 0 \\ - 3 - α & 3 (1 - m) (1 - p) + α & 3 ((1 - m) p + m q) & 3 m (1 - q) & 0 \\ 6 - 3 (1 - α) & - 3 (1 - m) (1 - p) - 3 α & - 3 ((1 - m) p + m q) & - 3 m (1 - q) & 0 \\ - 4 + 3 (1 - α) & 3 α & 0 & β & 1 - β \\ α & - α & 0 & - β & β \end{array}) (\begin{array}{l} b_{0} \\ b_{1} \\ b_{2} \\ \begin{array}{l} b_{3} \\ b_{4} \end{array} \end{array})$

其中， $(\begin{array}{l} 1 & t & t^{2} & t^{3} & t^{4} \end{array}) = T_{4} (t)$ 。

接下来令 $D_{4}^{u} = (\begin{array}{l} 0 & 0 & 0 \\ 3 (1 - m) (1 - p) + α & 3 ((1 - m) p + m q) & 3 m (1 - q) \\ - 3 (1 - m) (1 - p) - 3 α & - 3 ((1 - m) p + m q) & - 3 m (1 - q) \\ 3 α & 0 & β \\ - α & 0 & - β \end{array})$ ， $b_{4}^{u} = (\begin{matrix} b_{1} \\ b_{2} \\ b_{3} \end{matrix})$ ， $D_{4}^{v} = (\begin{array}{l} 1 & 0 \\ - 3 - α & 0 \\ 6 - 3 (1 - α) & 0 \\ - 4 + 3 (1 - α) & 1 - β \\ α & β \end{array})$ ， $b_{4}^{v} = (\begin{matrix} b_{0} \\ b_{4} \end{matrix})$ ，可以得到：

$b (t) = T_{4} (t) D_{4}^{u} b_{4}^{u} + T_{4} (t) D_{4}^{v} b_{4}^{v} .$ (3)

5.3. 带形状参数的四次DP曲线逼近圆锥曲线

在给定圆锥曲线 $C (t)$ 的情况下，利用带形状参数的四次DP曲线进行圆锥曲线逼近的关键问题是找到带形状参数的四次DP曲线的控制顶点 $b_{0}, b_{1}, b_{2}, b_{3}, b_{4}$ ，Davood Bakhshesh [9] 在2014年提出了一种基于DP曲线的圆锥曲线逼近算法，该算法利用最小二乘法将端点插值的任意阶DP曲线进行圆锥曲线逼近，本文主要采用该算法求出带形状参数的四次DP曲线的控制顶点。

为了找到带形状参数的四次DP曲线的控制顶点 $b_{0}, b_{1}, b_{2}, b_{3}, b_{4}$ ，令 $b_{0} = c_{0}$ ， $b_{4} = c_{2}$ ，且在 $L_{2}$ 范数下距离函数 $d (C (t), b (t))$ 最小化，

$\min (C (t), b (t)) = \sqrt{\int_{0}^{1} {‖ C (t) - b (t) ‖}^{2} d t} .$ (4)

将式(4)表示为矩阵形式：

$d (C (t), b (t)) = \sqrt{\int_{0}^{1} {‖ r (t) B_{2} G c - T_{4} (t) D_{4}^{v} b_{4}^{v} - T_{4} (t) D_{4}^{u} b_{4}^{u} ‖}^{2} d t} .$

为了使 $d$ 最小化，有 $\frac{\partial d^{2}}{\partial b_{4}^{u}} = 0$ ，即

$\int_{0}^{1} {(T_{4} (t) D_{4}^{u})}^{Τ} (r (t) B_{2} G c - T_{4} (t) D_{4}^{v} b_{4}^{v} - T_{4} (t) D_{4}^{u} b_{4}^{u}) d t = 0,$

化简为：

$\int_{0}^{1} {(T_{4} (t) D_{4}^{u})}^{Τ} r (t) B_{2} G c d t - \bar{H} b_{4}^{v} - H b_{4}^{u} = 0$ (5)

其中，

$\bar{H} = \int_{0}^{1} {(T_{4} (t) D_{4}^{u})}^{Τ} T_{4} (t) D_{4}^{v} d t = {(D_{4}^{u})}^{Τ} \int_{0}^{1} {(T_{4} (t))}^{Τ} T_{4} (t) d t D_{4}^{v} = {(D_{4}^{u})}^{Τ} {(x_{i, j})}_{i, j = 1}^{5} D_{4}^{v}, x_{i, j} = \frac{1}{i + j - 1},$

$H = \int_{0}^{1} {(T_{4} (t) D_{4}^{u})}^{Τ} T_{4} (t) D_{4}^{u} d t = {(D_{4}^{u})}^{Τ} \int_{0}^{1} {(T_{4} (t))}^{Τ} T_{4} (t) d t D_{4}^{u} = {(D_{4}^{u})}^{Τ} {(x_{i, j})}_{i, j = 1}^{5} D_{4}^{u} .$

由于对任意的非零3维列向量 $λ$ ，有 $λ^{Τ} H λ = \int_{0}^{1} {(T_{4} (t) D_{4}^{u} λ)}^{2} d t > 0$ ，则H为正定矩阵，且H可逆。

将式(5)中 $\int_{0}^{1} {(T_{4} (t) D_{4}^{u})}^{Τ} r (t) B_{2} G c d t$ 化简得到：

$\begin{matrix} \int_{0}^{1} {(T_{4} (t) D_{4}^{u})}^{Τ} r (t) B_{2} G c d t = {(D_{4}^{u})}^{Τ} \int_{0}^{1} r (t) {(T_{4} (t))}^{Τ} T_{4} (t) K G c d t \\ = {(D_{4}^{u})}^{Τ} \int_{0}^{1} r (t) {(T_{4} (t))}^{Τ} T_{4} (t) d t K G c \\ = L G c, \end{matrix}$

其中， $K = (\begin{array}{l} 1 & 0 & 0 \\ - 2 & 2 & 0 \\ 1 & - 2 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array})$ ， $L = {(D_{4}^{u})}^{Τ} \int_{0}^{1} r (t) {(T_{4} (t))}^{Τ} T_{4} (t) d t K$ 。

$\int_{0}^{1} r (t) {(T_{4} (t))}^{Τ} T_{4} (t) d t$ 可按如下方法 [8] 计算：

$\int_{0}^{1} r (t) {(T_{4} (t))}^{Τ} T_{4} (t) d t = \frac{1}{2 - 2 ω} \int_{0}^{1} \frac{t^{m}}{t^{2} - t + \frac{1}{2 - 2 ω}} d t (m = 0, 1, 2, \dots, 8)$ ，

设 $a = \frac{1}{2 - 2 ω}$ ，则

$\int_{0}^{1} \frac{1}{t^{2} - t + a} d t = {\begin{matrix} \frac{4}{\sqrt{4 a - 1}} \arctan \frac{1}{\sqrt{4 a - 1}} a > \frac{1}{4} \\ \frac{2}{\sqrt{1 - 4 a}} \ln | \frac{1 - \sqrt{1 - 4 a}}{1 + \sqrt{1 - 4 a}} | a < \frac{1}{4} \\ - 4 a = \frac{1}{4} \end{matrix} ，$ 且 $\int_{0}^{1} \frac{t}{t^{2} - t + a} d t = \frac{1}{2} \int_{0}^{1} \frac{1}{t^{2} - t + a} d t$ ，

当 $m \geq 2$ 时，有

$\begin{matrix} \int_{0}^{1} \frac{t^{m}}{t^{2} - t + a} d t = \sum_{s = 1}^{m - 1} \sum_{i = 0}^{[\frac{s - 1}{2}]} \frac{C_{s}^{2 i + 1} b^{i}}{(m - s) 2^{(s - 1)}} + \frac{1}{2^{m - 2}} (\sum_{s = 0}^{[\frac{m - 1}{2}]} C_{m}^{2 s + 1} b^{s} - 4 a \sum_{s = 0}^{[\frac{m}{2}] - 1} C_{m - 1}^{2 s + 1} b^{s}) \\ \times {\begin{array}{l} \frac{\arctan \sqrt{{(- b)}^{- 1}}}{\sqrt{- b}} & - 1 < ω < 1 \\ \frac{1}{2 \sqrt{b}} \ln | \frac{1 - \sqrt{b}}{1 + \sqrt{b}} | & ω > 1 or ω < - 1 \\ - 1 \overset{\begin{array}{l} \end{array}}{} & ω = - 1 \end{array}, \end{matrix}$

其中， $b = 1 - 4 a = \frac{- ω - 1}{1 - ω}$ 。

由此，可将式(5)化为：

$L G c - \bar{H} b_{4}^{v} - H b_{4}^{u} = 0.$ (6)

故得，

$b_{4}^{u} = H^{- 1} (L G c - \bar{H} b_{4}^{v})$ (7)

因此，带形状参数的四次DP曲线的控制顶点 $b_{0}, b_{1}, b_{2}, b_{3}, b_{4}$ ，可表示成如下形式：

$(\begin{matrix} b_{0} \\ b_{4}^{u} \\ b_{4} \end{matrix}) = (\begin{matrix} c_{0} \\ H^{- 1} (L G c - \bar{H} b_{4}^{v}) \\ c_{2} \end{matrix}) .$ (8)

5.4. 数值例子

例1：取圆锥曲线 $C (t)$ 的控制顶点为 $c_{0} = (0, 0)$ ， $c_{1} = (0.3, 1.5)$ ， $c_{2} = (1, 0)$ ，且 $ω = 0.8$ ，圆锥曲线 $C (t)$ 为椭圆(如图1(a))。令 $α = β = \frac{1}{2}, p = \frac{1}{4}, q = \frac{1}{3}, m = \frac{1}{5}$ ，利用上述算法求出带形状参数的四次DP曲线的控制点为

${\begin{cases} b_{0} = (0, 0), \\ b_{1} = (- \frac{457777}{5} + 284550 \arctan (\frac{1}{3}), - 504 (- 1287 + 4000 \arctan (\frac{1}{3}))), \\ b_{2} = (\frac{11107109}{40} - \frac{1726025}{2} \arctan (\frac{1}{3}), 21 (- 96002 + 298375 \arctan (\frac{1}{3}))) \\ b_{3} = (- \frac{407082}{5} + 253050 \arctan (\frac{1}{3}), - 504 (- 1287 + 4000 \arctan (\frac{1}{3}))), \\ b_{4} = (1, 0) . \end{cases},$

将带形状参数的四次DP曲线进行圆锥曲线逼近(如图1(b))，在 $L_{2}$ 范数下计算误差距离函数，这里，我们引入最大误差 $d_{\max} = \max_{0 \leq t \leq 1} {‖ C (t) - b (t) ‖}$ 来评估近似结果，可得到 $d_{\max} = 6.4178 \times 10^{- 4}$ 。

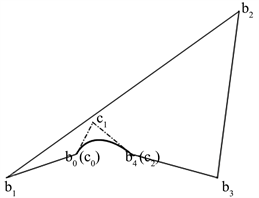(a)(b)

Figure 1. (a) The conic section $C (t)$ ; (b) The quartic DP curve with shape parameters when $α = β = \frac{1}{2}$ , $p = \frac{1}{4}$ , $q = \frac{1}{3}$ , $m = \frac{1}{5}$

图1. (a) 圆锥曲线 $C (t)$ ；(b) $α = β = \frac{1}{2}$ ， $p = \frac{1}{4}$ ， $q = \frac{1}{3}$ ， $m = \frac{1}{5}$ 时的带形状参数的四次DP曲线

例2：取圆锥曲线 $C (t)$ 的控制顶点为 $c_{0} = (0, 0)$ ， $c_{1} = (2, 1.2)$ ， $c_{2} = (1, 0)$ ，且 $ω = 1.2$ ，圆锥曲线 $C (t)$ 为双曲线(如图2(a))。令 $α = \frac{9}{10}$ ， $β = \frac{7}{8}$ ， $m = \frac{1}{2}$ ， $p = 1$ ， $q = \frac{10}{11}$ ，求出带形状参数的四次DP曲线的控制点为

${\begin{cases} b_{0} = (0, 0), \underset{\begin{array}{l} \end{array}}{} \\ b_{1} = (- \frac{5}{99} (11178101 + 5415375 \sqrt{11} \ln \frac{1}{5} (6 - \sqrt{11})), - \frac{336}{11} (14707 + 7125 \sqrt{11} \ln \frac{1}{5} (6 - \sqrt{11}))), \\ b_{2} = (\frac{6271266}{49} + \frac{4774250 \ln \frac{1}{5} (6 - \sqrt{11})}{7 \sqrt{11}}, \frac{8}{385} (4933082 + 2389875 \sqrt{11} \ln \frac{1}{5} (6 - \sqrt{11}))), \\ b_{3} = (- \frac{4021405}{7} - \frac{3061500 \ln \frac{1}{5} (6 - \sqrt{11})}{\sqrt{11}}, - \frac{1728}{55} (14707 + 7125 \sqrt{11} \ln \frac{1}{5} (6 - \sqrt{11}))), \\ b_{4} = (1, 0) . \end{cases}$

将带形状参数的四次DP曲线进行圆锥曲线逼近(如图2(b))，在 $L_{2}$ 范数下计算误差距离函数，得到 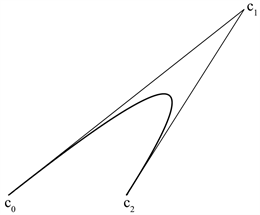$d_{\max} = 8.0494 \times 10^{- 4}$ 。

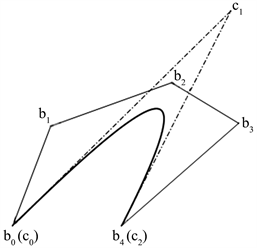(a)(b)

Figure 2. (a) The conic section $C (t)$ ; (b) The quartic DP curve with shape parameters when $α = \frac{9}{10}$ , $β = \frac{7}{8}$ , $m = \frac{1}{2}$ , $p = 1$ , $q = \frac{10}{11}$

图2. (a) 圆锥曲线 $C (t)$ ；(b) $α = \frac{9}{10}$ ， $β = \frac{7}{8}$ ， $m = \frac{1}{2}$ ， $p = 1$ ， $q = \frac{10}{11}$ ，时的带形状参数的四次DP曲线

文章引用

王研,宋九锡,秦凌云,沈洋,彭兴璇. 带形状参数的四次DP曲线的构造与应用
Construction and Application of the Quartic DP Curve with Shape Parameters[J]. 应用数学进展, 2021, 10(10): 3582-3591. https://doi.org/10.12677/AAM.2021.1010378

参考文献

1. Delgado, J. and Peña, J.M. (2003) A Shape Preserving Representation with an Evaluation Algorithm of Linear Complexity. Computer Aided Geometric Design, 20, 1-10. https://doi.org/10.1016/S0167-8396(02)00190-5

2. 陈杰, 王国瑾. 一类带形状参数的DP-NTP 曲线及其应用[J]. 计算机辅助设计与图形学学报, 2011, 23(6): 1055-1060.

3. 陈福来, 吴晓勤, 朱秀云. 广义三次DP曲线[J]. 计算机科学, 2012, 39(12): 264-267.

4. 彭兴璇, 蒋新昕, 谢宇迪. 一类带形状参数的三次DP曲线[J]. 计算机辅助设计与图形学学报, 2018, 30(9): 1712-1718.

5. 张迪, 查东东, 刘华勇. 三次DP曲线定义区间的扩展及其形状优化[J]. 浙江大学学报(理学版), 2020, 47(2): 178-190.

6. Floater, M.S. (1997) An O(h2n) Hermite Approximation for Conic Sections. Computer Aided Geometric Design, 14, 135- 151. https://doi.org/10.1016/S0167-8396(96)00025-8

7. Ahn, Y.J. (2010) Approximation of Conic Sections by Curvature Continuous Quartic Bézier Curves. Computers and Mathematics with Applications, 6, 1986-1993. https://doi.org/10.1016/j.camwa.2010.07.032

8. Hu, Q.Q. (2012) Approximating Conic Sections by Constrained Bézier Curves of Arbitrary Degree. Journal of Computational and Applied Mathematics, 236, 2813-2821. https://doi.org/10.1016/j.cam.2012.01.017

9. Bakhshesh, D. and Davoodi, M. (2014) Approximating of Conic Sections by DP Curves with Endpoint Interpolation. International Journal of Computer Mathematics, 92, 1-14. https://doi.org/10.1080/00207160.2014.889293

10. 张伟红, 蔡亦青, 冯玉瑜. 圆弧的五次PH曲线等弧长逼近[J]. 计算机辅助设计与图形学学报, 2010, 22(7): 1082-1086.

期刊菜单