Advances in Applied Mathematics
Vol.
10
No.
05
(
2021
), Article ID:
42837
,
10
pages
10.12677/AAM.2021.105193
基于T细胞和巨噬细胞的HIV感染模型研究
张雨婷,刘超艺,黄永学,王艳
中国石油大学(华东)理学院,山东 青岛
收稿日期:2021年4月27日;录用日期:2021年5月11日;发布日期:2021年5月31日

摘要
本文在HIV感染过程中,考虑两类靶细胞:整合速度快的CD4+ T细胞和整合速度慢的巨噬细胞,建立基于两类靶细胞的HIV感染模型。该模型主要包括感染细胞转化成正常细胞的恢复阶段。首先,定义模型的基本再生数,进而得到无病平衡点E0以及感染平衡点E*,并理论推导得到模型在两类平衡点的局部渐近稳定性。进一步地,通过利用Lasalle不变原理以及构造Lyapunov函数,得出,当R0 < 1时,无病平衡点E0是全局渐近稳定的。最后,通过查阅文献确定参数的实际范围,对模型进行数值模拟,验证稳定性理论的正确性。
关键词
HIV病毒,T细胞,巨噬细胞,Lyapunov函数,恢复阶段,稳定性分析
Study on the HIV Infection Model Based on T-Cell and Macrophage
Yuting Zhang, Chaoyi Liu, Hongxue Huang, Yan Wang
Science Department, China University of Petroleum (East China), Qingdao Shandong

Received: Apr. 27th, 2021; accepted: May 11th, 2021; published: May 31st, 2021

ABSTRACT
During the infection process, we consider two types of target cells: CD4+ T cells with a fast integration rate and macrophages with a slow integration rate, and establish an HIV infection model based on the two types of target cells. The main features of this model include the recovery phase of the transformed cells from infected cells into normal cells. We obtain the basic reproduction number R0, disease-free equilibrium point E0 and infection equilibrium point E* of the model, and theoretically derive the local asymptotic stability of the model at the two types of equilibrium points. Furthermore, by using Lasalle’s invariance principle and the Lyapunov function, we obtain that when R0 < 1, the disease-free equilibrium point E0 is globally asymptotically stable. Finally, the actual range of parameters is determined by consulting the literature, and the model is numerically simulated to verify the correctness of the stability theory.
Keywords:HIV Virus, T Cells, Macrophages, Lyapunov Function, Recovery Phase, Stability Analysis

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自1981年第一位艾滋病患者出现以来,艾滋病已在全世界传播,成为全球重大公共卫生问题。根据联合国艾滋病规划署数据 [1],全球范围内艾滋病病毒携带者和艾滋病患者人数从2013年末的3430万人增至2018年末的3790万人,携带者数量仍逐年增长。而截至2019年底,我国现存HIV/AIDS患者约129万,2019年新增感染者15万人,死亡4.2万人。
艾滋病,即获得性免疫缺陷综合征(Acquired Immuno Deficiency Syndrome, AIDS)。它是由艾滋病病毒(Human Immunodeficiency Virus, HIV)感染引起的慢性传染病疾病,HIV破坏人体免疫系统后,使人体缺乏对各种病原体的抵抗力,表现出复杂的免疫缺陷性疾病,严重时出现各种机会感染,甚至恶性肿瘤,自然病程中致死率高。
HIV侵入人体后,通过与细胞表面的受体结合,在辅助受体(fusin, CCR5等的)参与并相互作用下,主要感染CD4+ T淋巴细胞,并在其内增殖复制,使CD4+ T细胞大量损耗,病毒释放出至血液形成HIV血症,致使感染向全身扩散;更多的CD4+ T细胞被感染和破坏。HIV还通过其他受体,如Fc及补体受体、脑细胞及肠上皮细胞的半乳糖神经氢酸酶等感染其他细胞,HIV可侵入巨噬细胞,并随该细胞至体内许多组织,造成多脏器损伤。所以,除CD4+ T细胞外,HIV还感染单核巨噬细胞、滤泡树突状细胞、脑星状细胞、少突胶质细胞、血管内皮细胞、肠上皮细胞和肾脏组织细胞等,引起不同程度病理损害,而机体免疫系统首当其冲,损害也最严重。由于体内大量CD4+ T细胞被破坏和功能障碍,最终导致机体免疫缺陷。
2. 基于T细胞和巨噬细胞的HIV动力学模型
近年来,随着对感染动力学模型研究的愈发深入,模型的建立也越来越精确多样。在这里建立的模型如下 [2]:
(2-1)
其中,CD4+ T细胞 以输入率 产出, 表示其死亡率,感染CD4+ T细胞浓度为 ,感染系数为 。感染CD4+ T细胞的死亡率为 ,感染CD4+ T细胞转化为正常T细胞的转化率为 。巨噬细胞 以输入率 产出, 表示其死亡率,感染巨噬细胞浓度为 ,感染系数为 。感染巨噬细胞的死亡率为 ,感染巨噬细胞转化为正常巨噬细胞的转化率为 。病毒颗粒的浓度为 ,其中,感染CD4+ T细胞死亡后释放产生病毒,病毒释放率为 ,感染巨噬细胞死亡后释放产生病毒,病毒释放率为 ,病毒移除率为c,模型(2-1)的示意图如图1所示,模型中所有参数假定都是正的。
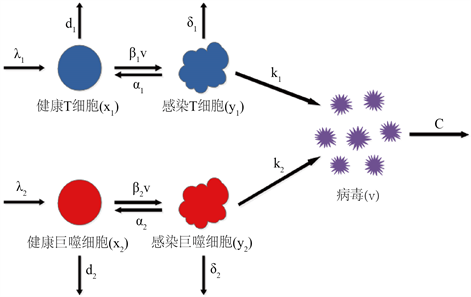
Figure 1. A schematic representation of the model system
图1. 模型系统的示意图
该模型考虑了两类靶细胞的影响以及感染细胞以一定比例恢复为正常细胞的生物学机理。
3. 模型平衡点
首先,通过平衡点的求解方法,令中各个方程右端为0,我们得到以下方程:
(3-1)
对于无病平衡点的求解,不妨设 ,那么 ,。通过化简,得出 ,。
我们可以得到无病平衡点 。
接着,定义基本再生数 ,它表示每个HIV病毒的存活期间所能感染健康T细胞和健康巨噬细胞的平均数量 [3]。
对于感染平衡点的求解,此时 ,由第一个式子和第二个式子可以得到 ,。同理,由第三个式子和第四个式子可以得到 ,。将 与 的表达式代入第五个式子整理得到方程
,由于 ,所以可以将分子上的 消去,由此可以得到
感染平衡点 ,
其中 满足
那么,假设当 时,
,
由基本再生数的定义,得到 ,而 ,,并且
,可以知道 是单调递减的,所以对于方程
,当 时有唯一的正解,当 时没有正解。
4. 平衡点的稳定性
4.1. 无病平衡点的局部稳定性
定理1 当 时,无病平衡点 是局部渐近稳定的。
当 时,无病平衡点 是不稳定的。
证明:模型(3-1)在无病平衡点 处的Jacobi矩阵为,令 ,即
得到特征方程:
整理得:
其中 。
那么 的局部渐近稳定性就取决于 的根。
(1) 当 时, ,,且 。所以
由零点定理得 在 上至少有一个根,所以 在 上是不稳定的。
(2) 当 时,假设 ,那么 满足 就可以得到
而 与 相矛盾,那么就可以得到 ,其中 。所以当 时, ,无病平衡点 是局部稳定的。
综上得出,当 时,无病平衡点 是局部渐近稳定的;当 时,无病平衡点 是不稳定的。
4.2. 无病平衡点的全局稳定性
定理2 当 且满足 时,无病平衡点 是全局渐近稳定的。
证明:通过定理1,当 时,无病平衡点 是局部渐近稳定的,那么证明它是全局吸引的。
不难看出对于所有的 ,每一个解都有 ,。因此不失一般性,可以构造出Lyapunov方程 [4] [5]
计算 导数,并带入 ,得到如下:
因此易得,当 时, 。此外, 当且仅当 , 成立。由
Lasalle不变集原理 [6],能够证明在 是全局吸引的。
所以,当 时,无病平衡点 是全局渐近稳定的。
4.3. 感染平衡点的局部稳定性
定理3当 时,感染平衡点 是局部渐近稳定的。
证明:模型(3-1)在感染平衡点 处的Jacobi矩阵为 ,令 ,即:
整理得:
假设 ,其中 满足 ,则可得到
由模型方程组的第五个式子: ,即 ,可以推出1 < 1,
产生矛盾,则 。
综上得出,当 时,感染平衡点 是局部渐近稳定的。
5. 数值模拟
在本部分中,将继续利用表1中给出的参数值对系统进行一些数值模拟,验证本文定理的正确性。根据参考文献 [7] 所给的范围,并结合文献 [8] 中的数据,将参数的含义,单位及其取值范围以及参数值列表1所示。
Table 1. The meaning and value of the parameters in the system (3-1)
表1. 系统(3-1)中参数含义与取值
使用多组初始数据进行数值模拟,且每组初始值的含义,单位和取值如表2所示。
Table 2. The initial value
表2. 初始值表
5.1. 数值模拟无病平衡点E0的稳定性
研究无病平衡点 的稳定性。首先将参数表1中的数据1代入系统(3-1)中,计算基本再生数 ,符合定理1与定理2条件,因此对于表1中的数据1的参数,系统在无病平衡点 处是全局渐近稳定的。选取表2中的多组数据进行模拟,如图2所示。
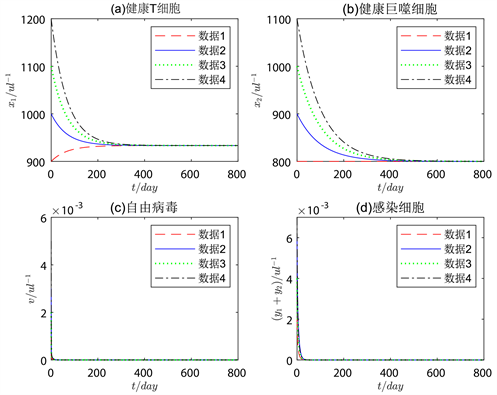
Figure 2. The local asymptotic stability of the uninfected equilibrium point of the system (3-1)
图2. 系统(3-1)的无病平衡点的局部渐近稳定性
从图2可以看出,所得到的数值模拟的结果趋近于无病平衡点 ,经过软件计算可以得到健康T细胞的值最终趋向于 ,感染T细胞趋向于 ,健康巨噬细胞的值趋向于 ,感染巨噬细胞趋向于 ,以及自由病毒趋向于 。而通过参数计算的平衡状
态是 ,其中 ,,对于感染T细胞、感染巨噬细胞以及
自由病毒均可看作趋向于0,因此可以认为系统在无病平衡点 处是局部渐近稳定的,而通过多组初值进行模拟,发现其最终结果都是一样的,所以可以认为 是全局吸引的,由此可以说,系统在无病平衡点 处是全局渐近稳定的。
5.2. 数值模拟感染平衡点E*的稳定性
对于系统(3-1)中各个参数使用表1中数据2,并计算基本再生数 ,符合定理3的条件,因此对于表1中的数据2的参数,系统在感染平衡点 处是全局渐近稳定的。使用表2中的几组数据进行多次实验,如图3所示。

Figure 3. The local asymptotic stability of the infected equilibrium point of the system (3-1)
图3. 系统(3-1)的感染平衡点的局部渐近稳定性
从图3可以得出,数值模拟的结果趋近于感染平衡点 ,经过Matlab计算得到健康T细胞浓度 趋近于151.5492,感染T细胞浓度 趋近于187.0053,健康巨噬细胞浓度 趋近于80.4896,感染巨噬细胞浓度 趋近于180.9427,自由病毒v趋近于3579.681。通过
这里 。将参数与 代入,得出健康T细胞浓度 ,感染T细胞浓度 ,健康巨噬细胞浓度 ,感染巨噬细胞浓度 ,并且
,把 代入,得到值为−0.001436,几乎为0。因此可
以得到系统(2-2)在感染平衡点处是局部渐近稳定的。
6. 结语
本文首先建立基于CD4+ T细胞和巨噬细胞的HIV感染模型,该模型考虑了两类靶细胞的影响以及感染细胞以一定比例恢复为正常细胞的生物学机理。
其后,求出两类平衡点,即无病平衡点与感染平衡点,并定义基本再生数 。进一步通过特征方程模的思想证明出当 时,无病平衡点 是局部渐近稳定的,当 时,感染平衡点 是局部渐近稳定的。而对于无病平衡点的全局稳定性,本文通过Lyapunov方法建立方程,并通过Lasalle不变集原理加以证明。最后,本文通过两组参数模拟无病平衡点和感染平衡点,通过多组初始数据进行数值模拟,验证得到理论分析的正确性,从而为相关医学工作者提供理论依据与数据支持。
基金项目
中国石油大学(华东)大学生创新创业训练计划资助项目(202012071)。
文章引用
张雨婷,刘超艺,黄永学,王 艳. 基于T细胞和巨噬细胞的HIV感染模型研究
Study on the HIV Infection Model Based on T-Cell and Macrophage[J]. 应用数学进展, 2021, 10(05): 1834-1843. https://doi.org/10.12677/AAM.2021.105193
参考文献
- 1. 联合国艾滋病规划署. 2019年全球艾滋病最新情况[EB/OL]. http://hkb980dd.pic44.websiteonline.cn/upload/0ezt.pdf, 2019-07-16.
- 2. Wang, X., Ge, Q. and Chen, Y. (2020) Threshold Dynamics of an HIV Infection Model with Two Distinct Cell Subsets. Applied Mathematics Letters, 103, Article ID: 106242. https://doi.org/10.1016/j.aml.2020.106242
- 3. Wang, W. and Zhao, X.Q. (2008) Threshold Dynamics for Compartmental Epidemic Models in Periodic Environments. Journal of Dynamics & Differential Equations, 20, 699-717. https://doi.org/10.1007/s10884-008-9111-8
- 4. 刘春美. Lyapunov方法在系统稳定性理论上的应用[D]: [硕士学位论文]. 长春: 东北师范大学, 2011.
- 5. Lv, C., Huang, L.H. and Yuan, Z.H. (2014) Global Stability for an HIV-1 Infection Model with Beddington-DeAngelis Incidence Rate and CTL Immune Response. Communications in Nonlinear Science and Numerical Simulation, 19, 121-127. https://doi.org/10.1016/j.cnsns.2013.06.025
- 6. Lasalle, J. (1976) The Stability of Dynamical Systems. SIAM, Philadelphia.
- 7. Yan, W., Zhou, Y., Brauer, F., et al. (2013) Viral Dynamics Model with CTL Immune Response Incorporating Antiretroviral Therapy. Journal of Mathematical Biology, 67, 901-934. https://doi.org/10.1007/s00285-012-0580-3
- 8. Hill, A.L., Rosenbloom, D., Nowak, M.A., et al. (2018) Insight into Treatment of HIV Infection from Viral Dynamics Models. Immunological Reviews, 285, 9-25. https://doi.org/10.1111/imr.12698
