Advances in Applied Mathematics
Vol.
12
No.
03
(
2023
), Article ID:
63194
,
12
pages
10.12677/AAM.2023.123130
一些图的Sombor指标
阿丽米热·吐尔洪,买吐肉孜·买司地克*
新疆师范大学数学科学学院,新疆 乌鲁木齐
收稿日期:2023年2月24日;录用日期:2023年3月21日;发布日期:2023年3月28日

摘要
Sombor指标是最近由Gutman引入的概念,是一种新的基于顶点度的拓扑指标,它是由
表示,其中
和
分别表示顶点
和
在G中的度。这种新的拓扑不变量被应用于化学图论领域。本文研究了扇图、轮图、一种特殊的仙人掌图、蝴蝶结图、荷兰风车图、棒棒糖图、杠铃图和风筝图以及四角格子图、六角格子图等化学图的Sombor指标。
关键词
Sombor指标,笛卡尔积,半笛卡尔积

Sombor Index for Some Graphs
Almire Turhun, Metrose Metsidik*
College of Mathematics Science, Xinjiang Normal University, Urumqi Xinjiang
Received: Feb. 24th, 2023; accepted: Mar. 21st, 2023; published: Mar. 28th, 2023

ABSTRACT
Sombor index is a concept recently introduced by Gutman. It is a new topological index based on vertex degree and represented by
, where
and
and degrees of vertices mean
and
in G. In this paper, this new topological index is applied in the area of chemical graph theory. In this paper, we study Sombor index of some chemical graphs such as fan graphs, wheel graphs, special cactus graphs, bow graphs, dutch windmill graphs, lollipop graphs, barbell graphs, kite graphs quadrangular grid graphs and hexagonal grid graphs.
Keywords:Sombor Index, Cartesian Product, Semi-Cartesian Product

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在本文中图G是具有顶点集
和边集
的简单图,记图
。图G中,边数记为
,点数(阶)记为
,
表示图G的最大度,
表示图G的最小度。
表示点
在图G中的度数。
表示t阶的圈,
表示t阶的路,
表示n阶的完全图。
在图自同构下不变的数称为图不变量,它通常被称为图的结构不变量。拓扑指标(TI)一般指与分子图论有关的图不变量。目前已有各种基于顶点度的图不变量被广泛介绍和研究 [1] ,它们通常被称为“拓扑指标” [2] ,其通式为:
其中的函数
具有交换律,即
。有序对
,其中
和
是边
的度坐标。例如
或
第一或第二Zagreb
指标,或者
是Sombor指标 [3] 。
Sombor指标的灵感来自于边的度半径的几何解释,对于图G的Sombor指标SO(G)定义为:
Gutman在文献 [3] 中建立了与Sombor指标相关的几个数学性质。这种新的拓扑指标被应用于化学图论领域,引起了化学图论研究人员的兴趣。化学图论中的分子图是化合物分子的结构表示,化合物分子中的每个原子都能看作是简单图中的一个点,每条边可以看作是原子之间的化学键,所以,可以用图论中的一个图来表示化合物的分子结构,将图论研究引入到化学领域中。化学家们发现,分子图拓扑指标值不仅可以在分子的结构及其性质之间建立联系,还可以定量的表达分子的结构。拓扑指标实际上通过转换化学结构生成的数值,这个数值会影响化合物的某些物理–化学性质。研究各类图的拓扑指标对科研以及生活的应用有着重大的意义。
Sombor指标自提出以来,受到了许多研究人员的关注,得到了很多新的研究成果。Randhir和Patekar在文献 [4] 中得出了
-分裂图和正则图的
-影子图的Sombor指标;Liu等人在文献 [2] 中得出了图的Sombor指标在各种结构参数下的界,以及Sombor指标与其他数值之间的关系,即一些树类、圈图、连通图以及化学图在各种结构参数下的界;Réti等人在文献 [5] 中推导了Sombor指标的一些界,并利用已有的结果建立了附加界,刻画出了具有最大Sombor指标的图,并提出了一个关于高圈图的最大Sombor指标的猜想;Cruz等人在文献 [6] 中确定了至多有三个分支顶点的树的Sombor指标的极值等。
学者们对某些特殊的简单图作了研究,但是对于一些特殊的简单图以及格子图的Sombor指标还未被研究得出精确的值,这方面存在欠缺。本文主要计算了还未被研究的一些特殊图类以及四角格子图和六角格子图的Sombor指标。
Sombor指标和图中的顶点度有直接的关系,根据所要研究的图的结构特点,我们可以先通过观察该图顶点数较少的情况,把它的顶点特征推广到任意顶点数的情况,给出对应图边集的划分,然后算出最后结论。
下面是本文所要研究的图的定义:
定义1. 笛卡尔积 [7] :设G和H是两个简单图,则图G和H的笛卡尔积由 表示(如图1为
表示(如图1为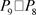 ),定义为:
),定义为:
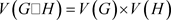
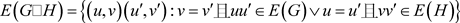
定义2. 半笛卡尔积 [8] :设G和H是两个连通的二部图,其分部集为白色和黑色,G是对称的,且H连通保圈可定向。则图G和H的半笛卡尔积由
表示(如图2为
),定义为:
,其中
在H的连通保圈定向上。
图1. 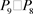
图2.
定义3. 特殊的仙人掌图 [9] :在圈
的每个点上连接一个3阶圈
,则得到一类特殊的仙人掌图,由
表示(如图3为
),它的点集和边集为
定义4. 轮图:通过将圈
上的每个点和一个外点都连边的图,由
表示(如图4为
)。
定义5. 扇图:轮图
删去圈上的任意一条边而得到的图,由
表示。
定义6. 蝴蝶结图:两个点数相同的扇图
通过粘贴中心点而得到的图,由
表示。
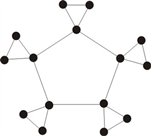
定义7. 荷兰风车图:通过粘贴n个圈
的一个公共顶点而得到的图,由
表示(如图5为
)。
图3.
图4. W8
图5.
定义8. 棒棒糖图:将一个路
连接在圈
上,由
表示。
定义9. 杠铃图:由两个互不相交的圈
,
和一个路
,其中这两个圈
和
通过
连接,由
表示。
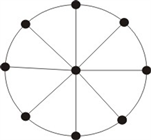
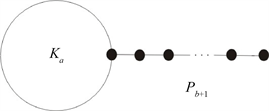
定义10. 风筝图:将一个路
连接在
上,由
表示(如图6所示)。
图6. La,b
2. 一些特殊图的Sombor(SO)指标
在本章将要讨论扇图,轮图,一种特殊的仙人掌图,蝴蝶结图,荷兰风车图,棒棒糖图,杠铃图以及风筝图的Sombor指标,并得出确切的值。
定理1. 荷兰风车图
的Sombor指标为
证明. 依次给出
的阶数和边数,显然有
和
。根据荷兰风车图的定义,
当
时它的最小度
和最大度
,
中恰有2n条边连接最小度点,有2n条边连接最小
度点和最大度点,所以它的Sombor指标为
□
定理2. 轮图
的Sombor指标为
证明.
和
,当
时最小度
,最大度
,由于
恰有n条边连接最小度点和最大度点,n条边连接最小度点,它的Sombor指标为
□
定理3. 扇图
的Sombor指标为
证明.
和
,当
时最小度
,最大度
,因为
恰有2条边连接最大度点和最小度点,
条边连接最大度点和
度点,2条边连接最小度点和
度点,
条边连接
度点,它的Sombor指标为
□
定理4. 蝴蝶结图
的Sombor指标为
证明.
和
,当
时最小度
,最大度
,当
时最小度
,最大度
。对于
,
恰有2条边连接最小度点,4条边连接最小度点和
最大度点,所以
对于
,
恰有4条边连接
度点和最小度点,有4条边连接最小度点和最大度点,
条边连接
度点和最大度点,
条边连接
度点,因而
□
定理5. 特殊的仙人掌图
的Sombor指标为
证明.
和
,由定义可知最小度
,最大度
,当
时,恰有n条边连接最小度点,n条边连接最大度点,2n条边连接最小度点和最大度点,所以它的Sombor指标为
□
定理6. 棒棒糖图
的Sombor指标为
证明.
和
,它的最小度
,最大度
,
恰有1条边连接最小度点和
度点,有3条边连接最大度点和
度点,有
条边连接
度
点,所以它的Sombor指标为
□
定理7. 杠铃图
的Sombor指标为
证明.
和
,它的最小度
,最大度
,
恰
有6条边连接最小度点和最大度点,有
条边连接最小度点,因此它的Sombor指标为
□
定理8. 对于风筝图
,它的Sombor指标为
证明.
和
,它的最小度
,最大度
,
当
时,
,由于路
的
,
,
;
当
时,
,由定理6可得
当
时,
恰有1条边连接最小度点和
度点,有
条边连接
度点,有1条连接最大度点和
度点,有
条边连接最大度点和
度点,有
条边连接
度点,因此它的Sombor指标为
,
□
3. 格子图的Sombor(SO)指标
在本章中将要计算四角格子图和六角格子图的Sombor指标的确切值,并得出格子图的Sombor指标与它因子图的Sombor指标之间的关系式。
3.1. 四角格子图的Sombor(SO)指标
平面四角格子图是由两条路
,
做笛卡尔积得到的图,由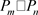 表示;环状四角格子图是由两个圈
和
做笛卡尔积得到的图,由
表示;环状四角格子图是由两个圈
和
做笛卡尔积得到的图,由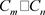 表示;柱状四角格子图是由圈
和路
做笛卡尔积所得到的图,由
表示;柱状四角格子图是由圈
和路
做笛卡尔积所得到的图,由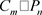 (或
(或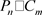 )表示。
)表示。
定理9. 平面四角格子图 的Sombor指标为
的Sombor指标为
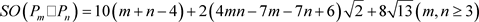
证明.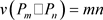 和
和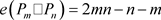 ,平面四角格子图的最大度
,平面四角格子图的最大度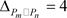 ,最小度
,最小度
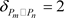 ,当
时,
,当
时,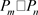 恰有8条边连接最小度点和
恰有8条边连接最小度点和 度点,有
条边连接
度点,有
条边连接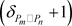 度点,有
条边连接最大度点和
度点,有
条边连接最大度点和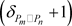 度点,有
条边连接
度点,有
条边连接
最大度点,所以它的Sombor指标为
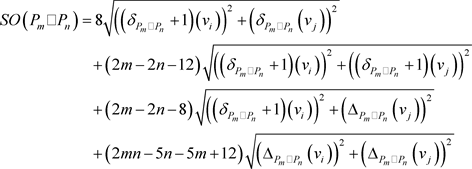
□
由于路
的
,则两条路
,
的Sombor指标与平面四角格子图的Sombor指标之间的关系式为:
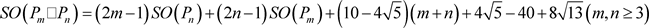 .
.
定理10. 环状四角格子图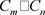 的Sombor指标为
的Sombor指标为
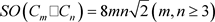
证明. 由文献 [4] 可知,若图G是n阶的k-正则图,则G的Sombor指标为
,显然,环
状四角格子图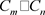 是一个mn阶的4-正则图,则
是一个mn阶的4-正则图,则
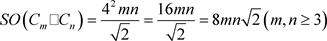 □
□
由于圈
的
,则两个圈
和
的Sombor指标与环状四角格子图的Sombor指标之间的关系式为:
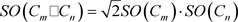 .
.
定理11. 柱状四角格子图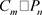 (或
(或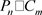 )
的Sombor指标为
)
的Sombor指标为
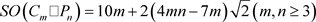 .
.
证明.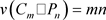 和
和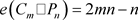 ,它的最小度
,它的最小度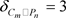 ,最大度
,最大度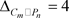 ,当
,当
时,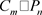 恰有2m条边连接最小度点,2m条边连接最小度点和最大度点,
条边连接最大度点,那么它的Sombor指标为
恰有2m条边连接最小度点,2m条边连接最小度点和最大度点,
条边连接最大度点,那么它的Sombor指标为
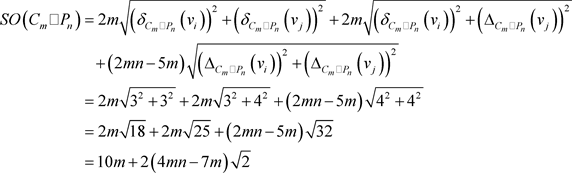 □
□
因为路
的
,圈
的
,则圈
和路
的Sombor指标与柱状四角格子图的Sombor指标之间的关系式为:
 .
.
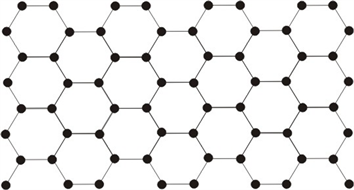
3.2. 六角格子图的Sombor(SO)指标
平面六角格子图是由两条路
,
做半笛卡尔积得到的图,由
表示;环状六角格子图是由两个圈
和
做半笛卡尔积得到的图,由
表示;柱状六角格子图是由圈
和路
做半笛卡尔积所得到的图,由
(或
)表示。
定理12. 平面六角格子图
(m为偶数)的Sombor指标为
证明.
,当n为偶数时,
,当n为奇数时,
,平面六角格子图的最小度
,最大度
,当n为奇数时,
恰有2条边连接最小度点和最大度点,有
条边连接最大度点,有
条边连接
度点,有
条边连接
度点和最大度点,因此它的Sombor指
标为
当n为偶数时,
恰有2条边连接最小度点和最大度点,
条边连接最大度
点,
条边连接
度点,
条边连接
度点和最大度点,则它的Sombor指标为
□
由于路
的
,则两条路
,
的Sombor指标与平面六角格子图的Sombor指标的关系式为:
当n为偶数时,
当n为奇数时,
定理13. 环状六角格子图
(
,
为偶数)的Sombor指标为
.
证明. 由文献 [4] 可知,若图G是n阶的k-正则图,则G的Sombor指标为
,显然,环
状六角格子图
是一个mn阶的3-正则图,则
□
由于圈
的
,则两个圈
,
(
,
为偶数) Sombor指标与环状六角格子图的Sombor指标的关系式为:
.
定理14. 柱状六角格子图
(
,m为偶数)的Sombor指标为
.
证明.
和
,它的最大度
,最小度
,
恰有2m条边连接最大度点和最小度点,
条边连接最大度点,则它的Sombor指标为
□
由于路
的
,圈
的
,则圈
和路
(
,m为偶数)的Sombor指标与柱状六角格子图的Sombor指标之间的关系式为:
.
定理15. 柱状六角格子图
(
,
为偶数)的Sombor指标为
.
证明.
和
,柱状六角格子图的最大度
,最小度
,当
,
为偶数时,它恰有n条边连接最小度点,有2n条边连接最大度点和最小度点,有
条边连接最大度点,所以它的Sombor指标为
□
由于路
的
,圈
的
,路
和圈
的(
,
为偶数)的Sombor指标与柱状六角格子图的Sombor指标之间的关系式为:
.
4. 总结
本文主要通过观察图的结构特点,给出对应图的边集的划分,进而确定了扇图、轮图、一种特殊的仙人掌图、蝴蝶结图、荷兰风车图、棒棒糖图、杠铃图、风筝图以及四角格子图和六角格子图的Sombor指标,并且得出了四角格子图和六角格子图的Sombor指标与它们的因子图的Sombor指标之间的关系,由于格子图的复杂性,对于Sombor指标的研究没有得到精美的结果,这个问题可继续研究。本文丰富了此领域格子图的研究成果。还可以进一步拓展研究未被研究的图的笛卡尔积和半笛卡尔积的Sombor指标,并得出与它的因子图的Sombor指标之间的关系。
文章引用
阿丽米热·吐尔洪,买吐肉孜·买司地克. 一些图的Sombor指标
Sombor Index for Some Graphs[J]. 应用数学进展, 2023, 12(03): 1281-1292. https://doi.org/10.12677/AAM.2023.123130
参考文献
- 1. De, N., Cancan, M., Alaeiyan, M. and Farahani, M.R. (2020) On Some Degree Based Topological Indices of Mk-Graph. Journal of Discrete Mathematical Sciences and Cryptography, 23, 1183-1194.
https://doi.org/10.1080/09720529.2020.1809112
- 2. Liu, H., Gutman, I., You, L. and Huang, Y. (2022) Sombor Index: Review of Extremal Results and Bounds. Journal of Mathematical Chemistry, 60, 771–798.
- 3. Gutman, I. (2021) Geometric Approach to Degree-Based Topological Indices: Sombor Indices. MATCH Communications in Mathematical and in Computer Chemistry, 86, 11-16.
- 4. Singh, R. and Patekar, S.C. (2022) On the Sombor Index and Sombor Energy of M-Splitting Graph and M-Shadow Graph of Regular Graphs. arXiv preprint arXiv:2205.09480.
- 5. Réti, T., Doli, T. and Ali, A. (2021) On the Sombor Index of Graphs. Contributions to Mathe-matics, 3, 11-18.
https://doi.org/10.47443/cm.2021.0006
- 6. Cruz, R., Rada, J. and Sigarreta, J.M. (2021) Sombor Index of Trees with at Most Three Branch Vertices. Applied Mathematics and Computation, 409, Article ID: 126414. https://doi.org/10.1016/j.amc.2021.126414
- 7. Imrich, W. and Klavzar, S. (2000) Product Graphs: Structure and Recognition. Wiley, New York.
- 8. Metsidik, M. (2014) Semi-Cartesian Product of Graphs. Journal of Mathematical Chemistry, 52, 856-865.
https://doi.org/10.1007/s10910-013-0297-6
- 9. 张东翰. 一类特殊图的星边染色[J]. 甘肃科学学报, 2021, 33(5): 26-28.
NOTES
*通讯作者。






 表示(如图1为
表示(如图1为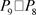 ),定义为:
),定义为: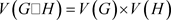
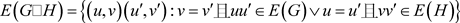
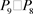
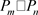 表示;环状四角格子图是由两个圈
和
做笛卡尔积得到的图,由
表示;环状四角格子图是由两个圈
和
做笛卡尔积得到的图,由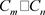 表示;柱状四角格子图是由圈
和路
做笛卡尔积所得到的图,由
表示;柱状四角格子图是由圈
和路
做笛卡尔积所得到的图,由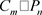 (或
(或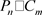 )表示。
)表示。 的Sombor指标为
的Sombor指标为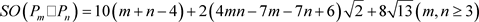
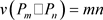 和
和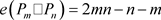 ,平面四角格子图的最大度
,平面四角格子图的最大度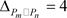 ,最小度
,最小度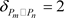 ,当
时,
,当
时,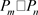 恰有8条边连接最小度点和
恰有8条边连接最小度点和 度点,有
条边连接
度点,有
条边连接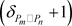 度点,有
条边连接最大度点和
度点,有
条边连接最大度点和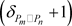 度点,有
条边连接
度点,有
条边连接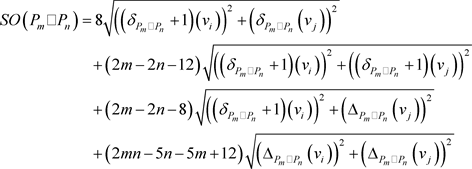
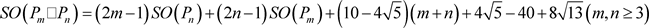 .
.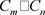 的Sombor指标为
的Sombor指标为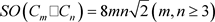
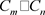 是一个mn阶的4-正则图,则
是一个mn阶的4-正则图,则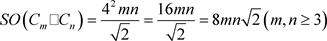 □
□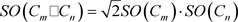 .
.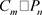 (或
(或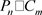 )
的Sombor指标为
)
的Sombor指标为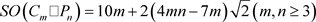 .
.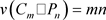 和
和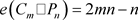 ,它的最小度
,它的最小度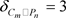 ,最大度
,最大度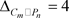 ,当
,当
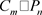 恰有2m条边连接最小度点,2m条边连接最小度点和最大度点,
条边连接最大度点,那么它的Sombor指标为
恰有2m条边连接最小度点,2m条边连接最小度点和最大度点,
条边连接最大度点,那么它的Sombor指标为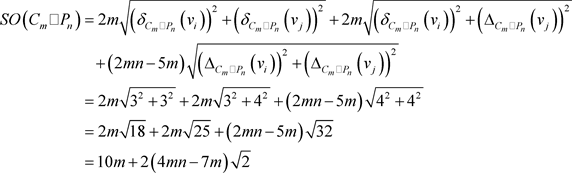 □
□ .
.