含直流潮流控制器的多端高压直流输电网络的小信号稳定性分析及控制系统设计 Small-Signal Stability Analysis and Control System Design of a Meshed Multi-Terminal High-Voltage Direct Current Grid with a Current Flow Controller

doi:10.12677/JEE.2019.71005

Journal of Electrical Engineering
Vol. 07 No. 01 ( 2019 ), Article ID: 29262 , 9 pages
10.12677/JEE.2019.71005

Small-Signal Stability Analysis and Control System Design of a Meshed Multi-Terminal High-Voltage Direct Current Grid with a Current Flow Controller

Xiaolei Sun, Wei Yang

●How to Cite this Article

College of Automation, Nanjing University of Science and Technology, Nanjing Jiangsu

Received: Feb. 21^st, 2019; accepted: Mar. 7^th, 2019; published: Mar. 15^th, 2019

ABSTRACT

In a high-voltage direct current (HVDC) grid, a DC power flow controller can be used to control the branch current, but it also affects the stability of the entire HVDV system. Therefore, it is necessary to study the dynamic characteristics of HVDC grid with a DC current flow controller (CFC). This paper focuses on the small-signal stability analysis of a three-terminal HVDC system with a DC CFC. Firstly, a small-signal mathematical model is built based on the existing three-terminal HVDC network with a DC CFC, secondly, on this basis, the control strategy for the DC CFC is designed to achieve the stability requirements of the entire system. Finally, a three-terminal HVDC simulation model with a DC CFC is established in Simulink. The proposed control strategy is verified under steady-state and transient operating conditions, and the simulation results are compared with the theoretical values. The dynamic influence of the DC CFC on the HVDC system is also discussed.

Keywords:High-Voltage Direct Current (HVDC), DC Current Flow Controller (CFC), Small-Signal Model, Dynamic Simulation, Stability Analysis

含直流潮流控制器的多端高压直流输电网络的小信号稳定性分析及控制系统设计

孙晓蕾，杨伟

南京理工大学自动化学院，江苏南京

收稿日期：2019年2月21日；录用日期：2019年3月7日；发布日期：2019年3月15日

摘要

在高压直流(HVDC)网络中，直流潮流控制器可以用来控制支路电流，但其同时也会影响整个HVDC系统的稳定性。因此，对于含直流潮流控制器的HVDC网络动态特性分析的研究必不可少。本文主要研究带直流潮流控制器的三端HVDC系统的小信号稳定分析。首先，基于已有的带直流潮流控制器的三端HVDC网络，搭建了小信号数学模型；其次在此基础上设计了对于直流潮流控制器的控制策略，实现整个系统的稳定要求。最后，在Simulink中建立带直流潮流控制器的三端HVDC仿真模型，在稳态和暂态运行工况下对所提控制策略进行仿真验证，并将其仿真结果与理论值进行对比，以此验证了直流潮流控制器对HVDC系统的动态影响。

关键词 :高压直流输电，直流潮流控制器，小信号模型，暂态仿真，稳定性分析

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

随着电力电子技术日益成熟，特高压直流及柔性直流输电技术广泛并入传统电力系统中，直流输电技术已成为电网发展的重要方向 [1] [2] [3] [4] [5]。与传统交流电网的发展类似，直流电网的拓扑必然会逐渐由辐射状向环状发展 [6] [7]。然而，环状直流网络相对于辐射状网络存在的主要问题是，环网线路上的电流不可控。因此，在多端直流环网系统中引入直流潮流控制装置，可以较大范围地控制潮流，使之按指定路径流动，并最大限度地利用线路容量。

目前，国内外学者已提出了三种直流潮流控制器设计方案，分别为在直流线路中接入可变电阻 [8] [9] 、直流变换器 [10] [11] [12] [13] [14] 和等效电压源 [15] [16] [17] [18] [19]。与前两者相比，等效电压源所需的电压和功率等级一级功率损耗都小得多，且易于实现。同时，通过接入等效电压源实现直流线路潮流控制主要有两种方法，一种需要外接电源 [15] [17] [18]，另一种则无需外接电源 [16] [19]。

对于现有的可变电压源型直流潮流控制方法，多数需要与外部交流电源连接来实现与直流网络的能量传输 [18] [19] [20]。只有两种直流潮流控制器(PFC)拓扑结构能避免使用外接的直流或交流电源 [16] [21] [22]。这种直流潮流控制器(CFC)或PFC有利于简化电路结构，并且无需外接交流电源。文献 [16] 主要介绍了CFC的结构，但并没有给出具体的控制策略。文献 [22] 研究了CFC的稳态模型，但是稳态模型并不能准确地揭示系统的动态特性和系统稳定性。加入了CFC之后，原先的HVDC系统很可能变得不再稳定。因此，对含有CFC的HVDC系统建立小信号模型至关重要。小信号模型广泛地应用于非线性系统的分析。通过对小信号模型进一步的研究，可以得到系统特征根值和传递函数，以此便可研究系统的稳定性及其动态特性。此外，基于小信号模型，可以设计控制系统来获得理想的系统动态响应。

综合以上诸多因素，本文主要工作在于研究含CFC的三端HVDC系统的小信号模型稳定性和对其控制环节的设计。主要体现在以下两个方面。1) 对于系统小信号模型的进一步研究，包括：a) CFC的动态分析；b) 对于CFC电压和有功功率控制的动态分析；c) DC网络的动态分析。2) 基于小信号模型的建立，对于DC CFC设计了控制环节，以此满足系统稳态及动态运行需求。同时，本文基于MATLAB/SimPowerSystem建立了系统仿真模型，以此验证小信号模型的稳定性和对于DC CFC设计的控制策略。并给出此仿真结果与理论数学模型运行结果的比价。最后，本文还分析了直流装置对多端HVDC网络的影响。

2. 含CFC的三端VSC-HVDC系统

2.1. 系统结构

典型的含两线路的三端VSC-HVDC系统等效电路如图1所示。三端分别为T₁、T₂和T₃，换流站采用VSC结构，直流环网线路采用电感和电阻串联的结构，且三端间设置线路参数不同。

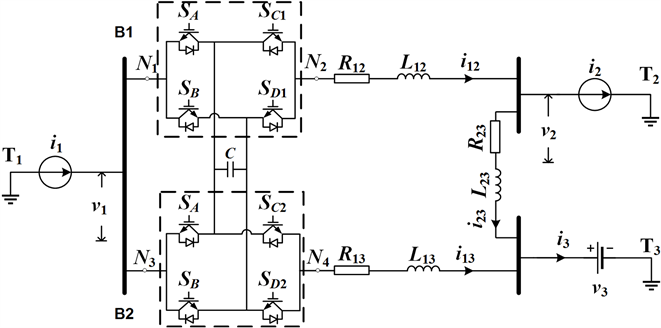
Figure 1. Meshed 3-T VSC HVDC grid with the installation of a CFC

图1. 含CFC的三端VSC-HVDC系统结构

2.2. VSC控制策略

如图1所示，T₁和T₂端的VSC采用定有功功率和定无功功率控制来稳定直流侧的电流值；而T₃端则采用定直流电压和定有功功率控制来稳定直流侧的电压值。因此，T₁、T₂端的VSC等效为直流电流源，T₃端的VSC则等效为直流电压源。

VSC能调节换流站端口间的总功率，但并不会改变各直流支路上的电流值。因此，各支路上的电流值会因线路参数的不同而产生不同。在不加以任何控制的情况下，支路电流很容易出现过载现象。为此，就必须在直流线路上加设专门的附加装置来控制各支路的电流，也就是我们所说的直流潮流控制器CFC。

2.3. CFC

如图1所示，将CFC安置在12和13支路间，它主要包括两个全桥型的直流变流器，并在两桥间并联一个电容，以此实现两个变流器间的能量传输。由此，只需改变并联电容的值就能控制各支路间的电流。

对于两线路CFC的控制，一般采用支路电流控制和电容电压控制相结合的策略。通过直流电流控制策略来控制12支路上的桥臂开关S_C₁，以此调节支路电流i₁₂；同样地，通过电容电压控制策略来控制13支路上的桥臂开关S_C₂，以此调节并联电容C上的电容电压。

如图1所示，全桥直流控制器由可控开关器件IGBT构成。通过调节PWM触发信号的占空比来控制开关的导通与闭合，以此实现线路直流潮流控制。CFC中各开关元件PWM信号的占空比如表1所示。

Table 1. Duty cycles of the PWM signals for the switches in the CFC

表1. CFC中开关元件PWM信号的占空比

通过控制四个开关的不同组合形式，每个CFC全桥都有如下四种工作模式，如表2所示。a_i为上桥B1各模式下开关的占空比；b_j为下桥B2各模式下开关的占空比。i_cfc₁、i_cfc₂分别为从B1、B2流经CFC电容C的电流值，u_c为电容C上的电压。i₁₂、i₁₃分别表示支路12、13上的支路电流；e₁₂、e₁₃则分别表示图1中N₁、N₂和N₃、N₄节点间的电压。

就上桥B1来看，在模式1下，开关S_A₁、S_C₁闭合，电容C没有接入支路12中，因此e₁₂、i_cfc₁都为0；在模式2下，开关S_A₁、S_D₁闭合，电容C没有接入支路12中，则e₁₂等于电容电压u_c，i_cfc₁等于支路电流i₁₂；在模式3下，开关S_B₁、S_C₁闭合，电容C向支路12放电，此时e₁₂等于−u_c，i_cfc₁等于−i₁₂；在模式4下，同模式1，电容C被旁路。同理，下桥B2分析与B1相同。

Table 2. Switch modes of bridge converters in the CFC

表2. CFC中开关模式

3. 系统数学建模

3.1. 系统等效电路

由上章的分析可知，对于所在支路，CFC相当于一个可控电压源。则整个系统的等效电路如图2所示，在支路12和13中，CFC分别等效为e₁₂和e₁₃。T₁、T₂端的等效模型为直流电流源i₁、i₂，同时并联接地电容Cs；T₃端等效模型为直流电压源v₃。

Figure 2. Equivalent representation of the whole system

图2. 系统等效电路

3.2. CFC数学模型

根据上述开关工作模式的分析，由叠加原理可得e₁₂、e₁₃与u_c的关系为

$\begin{array}{l} e_{12} = (a_{2} - a_{3}) u_{c} \\ e_{13} = (b_{2} - b_{3}) u_{c} \end{array}$

考虑电容C在一个开关周期内的充放电情况，可得u_c与i₁₂、i₁₃之间的关系为

$C \frac{d u_{c}}{d t} = (a_{2} - a_{3}) i_{12} + (b_{2} - b_{3}) i_{13}$

结合表1中的开关占空比，上两式可以改写为

$\begin{array}{l} e_{12} = (d_{a} - d_{c 1}) u_{c} \\ e_{13} = (d_{a} - d_{c 2}) u_{c} \\ C \frac{d u_{c}}{d t} = (d_{a} - d_{c 1}) i_{12} + (d_{a} - d_{c 2}) i_{13} \end{array}$

上式构成了CFC的动态数学模型，如上章所述，CFC等效为一个对支路12的可控电压源e₁₂和一个对支路13的可控电压源e₁₃。且通过改变d_c₁和d_c₂的值来控制e₁₂、e₁₃的大小。由此可见，CFC可以独立控制不同支路。

3.3. HVDC网络数学模型

由KVL、KCL定理，可以得到HVDC网络的数学模型

$\begin{array}{l} L_{12} \frac{d i_{12}}{d t} + R_{12} i_{12} = v_{1} - v_{2} - e_{12} \\ L_{13} \frac{d i_{13}}{d t} + R_{13} i_{13} = v_{1} - v_{3} - e_{13} \\ L_{23} \frac{d i_{23}}{d t} + R_{23} i_{23} = v_{2} - v_{3} \\ C_{s} \frac{d v_{1}}{d t} = i_{1} - i_{12} - i_{13} \\ C_{s} \frac{d v_{2}}{d t} = i_{12} - i_{23} - i_{2} \end{array}$

建立系统状态空间方程：

$\begin{array}{l} \dot{x} = A x + B v_{i n} \\ y = C x + D v_{i n} \end{array}$

其中，矩阵A、B、C、D将在附录中具体给出。式中，x为状态矢量，v_in和y分别为系统输入、输出矢量，它们可以分别表示为

$\begin{array}{l} x = {[\begin{matrix} i_{12} & i_{13} & i_{23} & v_{1} & v_{2} & u_{c} \end{matrix}]}^{T} \\ v_{i n} = {[\begin{matrix} i_{1} & i_{2} & v_{3} \end{matrix}]}^{T} \\ y = {[\begin{matrix} i_{12} & u_{c} \end{matrix}]}^{T} \end{array}$

输入量为来自三端VSC的可控电压和电流值，两个输出量为CFC控制的潮流值。在以下的研究中，取d_a、d_b的值都为0.5。

4. 小信号分析

绘制如图3所示的控制框图。图中，A₂、B_c、B_d、C₂为式(9)中的系统矩阵。虚线框中构成整个开环控制系统，解释了从控制输入v_c和小扰动输入v_d到输出y的两个控制环。接着，通过矩阵F将y反馈到y_f后，再与参考值y_ref进行比较。比较值e_r通过矩阵E后重回到控制量v_c。在下面的章节中，将具体介绍开环控制系统、控制矩阵E的设计以及闭环控制系统。

Figure 3. System transfer diagram based on the small-signal model

图3. 基于小信号模型的系统框图

4.1. 开环控制系统

从图3中可知，开环控制系统可表示为

$\begin{array}{l} \dot{x} = A_{2} x + B_{c} v_{c} + B_{d} v_{d} \\ y = C_{2} x \end{array}$

4.2. 控制环节(E)设计

本文对控制环节E采用了两个PI控制环，则矩阵E可表示为

$E = [\begin{matrix} \frac{P I_{1}}{i_{12 r e f}} & 0 \\ 0 & \frac{P I_{2}}{i_{12 r e f}} \end{matrix}] = [\begin{matrix} \frac{K_{P 1} + K_{I 1} / s}{i_{12 r e f}} & 0 \\ 0 & - \frac{K_{P 2} + K_{I 2} / s}{u_{c r e f}} \end{matrix}]$

式中，K_P₁、K_I₁、K_P₂、K_I₂分别为控制环PI₁和PI₂的参数。通过对以上四个参数的合理设置，以达到矩阵E的控制目标。

4.3. 闭环控制系统

如图4所示，将输出y_f返回到与参考值y_ref作比较，系统传递函数就变成闭环形式。则闭环下系统状态空间方程为

$\begin{array}{l} \dot{x} = A_{2} x + B_{c} E (y_{r e f} - F C_{2} x) + B_{d} v_{d} \\ y = C_{2} x \end{array}$

5. 仿真结果

在MATLAB/SimPowerSystem中建立图1中所示的三端VSC-HVDC仿真模型，以此来验证本文的控制器设计及理论分析。系统参数如表3所示。

Table 3. Parameters of the meshed 3-T VSC-HVDC system

表3. 三端VSC-HVDC系统参数

5.1. 工况1：i_12ref阶跃变化

初始时，i_12ref设为0.5 kA，在时间t为0.5 s时，i_12ref增加到0.6 kA，最后在t为1 s时再回到初始值0.5 kA。图4显示了此情况下i₁₂和u_c的动态响应，同时在图中对比了通过基于MATLAB的数学模型和基于 MATLAB/SimPowerSystem下仿真模型下的不同运行结果。

在动态响应过程中，i₁₂能在很短的时间达到新的参照值，并产生很小的误差。同时，u_c会出现很小的波动，但整体始终保持在稳定值。此外，不难发现，仿真模型的结果能很好的匹配理论模型下的结果，这就验证了本文所设计的控制器(E)是有效可行的。

Figure 4. System dynamic response to a step change of i_12ref

图4. i_12ref阶跃变化下的系统动态响应

5.2. 工况2：u_cref阶跃变化

初始时，u_cref设为3 kV，在时间t为0.5 s时，u_cref增加到3.3 kV，最后在t为1 s时再回到初始值3 kV。图5显示了此情况下i₁₂和u_c的动态响应，u_c能在很短的时间跟随u_cref变化，并产生很小的误差。同时，由于CFC电容的充放电，i₁₂也只会出现很小的波动，而整体稳定在参考值i_12ref。

Figure 5. System dynamic response to a step change of u_cref

图5. u_cref阶跃变化下的系统动态响应

6. 结论

1) 本文主要建立了含CFC的三端直流网络的小信号模型，并设计了对CFC的控制环节。基于已建立的小信号模型，此控制环节满足了系统稳定及动态特性的要求。

2) 本文通过与MATLAB/SimPowerSystem仿真结果的比较，验真了小信号模型的准确性；并通过不同工况下的运行结果，验证了本文所设计的控制系统的有效性。

文章引用

孙晓蕾,杨伟. 含直流潮流控制器的多端高压直流输电网络的小信号稳定性分析及控制系统设计
Small-Signal Stability Analysis and Control System Design of a Meshed Multi-Terminal High-Voltage Direct Current Grid with a Current Flow Controller[J]. 电气工程, 2019, 07(01): 44-52. https://doi.org/10.12677/JEE.2019.71005

参考文献

1. 于亚男, 金阳忻, 江全元, 等. 基于RT-LAB的柔性直流配电网建模与仿真分析[J]. 电力系统保护与控制, 2015, 43(19): 125-130.

2. 孙刚, 时伯年, 赵宇明, 等. 基于MMC的柔性直流配电网故障定位及保护配置研究[J]. 电力系统保护与控制, 2015, 43(22): 127-133.

3. 和敬涵, 李智诚, 王小君. 柔性直流环节对配电网优化运行作用的概率评估[J]. 中国电机工程学报, 2016, 36(2): 342-349.

4. 季一润, 袁志昌, 孙谦浩, 等. 柔性直流配电网典型运行方式及切换方法[J]. 南方电网技术, 2016, 40(13): 141-146.

5. 韩永霞, 何秋萍, 赵宇明, 等. 采用柔性直流技术的智能配电网接入交流电网方式[J]. 电力系统自动化, 2016, 10(4): 8-15.

6. Asplund, G., Lindén, K. and Barker, C. (2013) HVDC Grid Feasibility Study. Electra, 533, 50-59.

7. Vrana, T.K., Yang, Y. and Jovcic, D. (2013) The CIGRE B4 DC Grid Test System. CIGRE Electra Magazine, 270, 10-19.

8. Mu, Q., Liang, J., Lou, Y., et al. (2012) Power Flow Control Devices in DC Grids. IEEE Power and Energy Society General Meeting, San Diego, CA, 22-26 July 2012, 1-7.

9. Jovcic, D., Hajian, M., Zhang, H., et al. (2012) Power Flow Control in DC Transmission Grids Using Mechanical and Semiconductor Based DC/DC Devices. 10th IET International Conference on AC and DC Power Transmission, Birmingham, UK, 19-21 October 2010, 1-6. https://doi.org/10.1049/cp.2012.1972

10. Jovcic, D. and Ooi, B.-T. (2010) Developing DC Transmission Networks Using DC Transformers. IEEE Transactions on Power Delivery, 25, 2535-2543. https://doi.org/10.1109/TPWRD.2010.2052074

11. Kish, G.J., Ranjram, M. and Lehn, P.W. (2015) A Modular Multilevel DC/DC Converter with Fault Blocking Capability for HVDC Interconnects. IEEE Transactions on Power Electronics, 30, 148-162. https://doi.org/10.1109/TPEL.2013.2295967

12. 王朝辉, 王天威, 张军明. 模块化多电平直流变压器研究[J]. 中国电机工程学报, 2016, 36(1): 31-39.

13. 李建国, 赵彪, 宋强, 等. 直流配电网中高频链直流变压器的电压平衡控制策略研究[J]. 中国电机工程学报, 2016, 36(2): 327-334.

14. 孙长江, 张建文, 蔡旭, 等. 隔离型MMC直流变压器的电流源运行[J]. 中国电机工程学报, 2016, 36(7): 1977-1986.

15. Veilleux, E. and Ooi, B.-T. (2012) Multi-Terminal HVDC with Thyristor Power Flow Controller. IEEE Transactions on Power Delivery, 27, 1205-1212. https://doi.org/10.1109/TPWRD.2012.2187463

16. Barker, C.D. and Whitehouse, R.S. (2012) A Current Flow Controller for Use in HVDC Grids. 10th IET International Conference on AC and DC Power Transmission, Birmingham, 1-5.

17. Xu, F. and Xu, Z. (2014) A Modular Multilevel Power Flow Controller for Meshed HVDC Grids. Science China Technological Sciences, 57, 1773-1784. https://doi.org/10.1007/s11431-014-5620-3

18. 姚良忠, 崔红芬, 李官军, 等. 柔性直流电网串联直流潮流控制器及其控制策略研究[J]. 中国电机工程学报, 2016, 36(4): 945-952.

19. Chen, W., Zhu, X., Yao, L., et al. (2015) An Interline DC Power-Flow Controller (IDCPFC) for Multiterminal HVDC System. IEEE Transactions on Power Delivery, 30, 2027-2036. https://doi.org/10.1109/TPWRD.2015.2425412

20. Xu, F. and Xu, Z. (2014) A Modular Multilevel Power Flow Controller for Meshed HVDC Grids. Science China Technological Sciences, 57, 1773-1784. https://doi.org/10.1007/s11431-014-5620-3

21. Chen, W., Zhu, X., Yao, L., Ruan, X., Wang, Z. and Cao, Y. (2015) An Interline DC Power Flow Controller (IDCPFC) for Multiterminal HVDC System. IEEE Transactions on Power Delivery, 30, 2027-2036. https://doi.org/10.1109/TPWRD.2015.2425412

22. Deng, N., Wang, P., Zhang, X.-P., Tang, G.F. and Cao, J.Z. (2015) A DC Current Flow Controller for Meshed Modular Multilevel Converter Multiterminal HVDC Grids. CSEE Journal of Power and Energy Systems, 1, 43-51. https://doi.org/10.17775/CSEEJPES.2015.00006

期刊菜单