Finance
Vol.07 No.01(2017), Article ID:19565,9
pages
10.12677/FIN.2017.71005
A Statistical Arbitrage Strategy in Forex Market Based on High-Frequency Data
Dunjian Xiao1, Xiaowei Deng2, Bingqian Xia1
1Overseas Education College, Nanjing Tech University, Nanjing Jiangsu
2School of Physical and Mathematical Sciences, Nanjing Tech University, Nanjing Jiangsu

Received: Dec. 24th, 2016; accepted: Jan. 15th, 2017; published: Jan. 18th, 2017
Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In capital market, arbitrage is an essential trading method to avoid risks. Statistical arbitrage, which is a genre of arbitrage, has been widely utilized by foreign financial institutions since several decades ago. Since lacking of Short Hedge Mechanism, statistical arbitrage can hardly be realized in domestic capital markets. However, the situation is being relieved with the introduction of margin trading and stock index futures. And the trend to set up Short Hedge Mechanism is overwhelming. In this dissertation, we tested the arbitrage chances in forex market by adopting the thought of statistical arbitrage, combining with cointegration modeling and every minute’s closing rate of EUR/USD and CHR/JPY, which are highly correlated with each other, within 24 hours. After studying in the time series of price difference, we found that there were abundant opportunities for arbitrage. Hence, we are able to give out a novel quantified path for investors in the future.
Keywords:Statistical Arbitrage, High-Frequency Data, Cointegration Model, Forex Trading

一种基于高频数据的汇市统计套利策略
肖敦健1,邓晓卫2,夏冰倩1
1南京工业大学海外教育学院,江苏 南京
2南京工业大学数理科学学院,江苏 南京

收稿日期:2016年12月24日;录用日期:2017年1月15日;发布日期:2017年1月18日

摘 要
资本市场中,套利交易是一种规避风险的重要交易方式。统计套利在近几十年来在国外资本市场十分盛行。而国内资本市场由于缺乏做空机制,统计套利等量化投资策略很难得以实现。而近年来随着融资融券和股指期货的推出,这一局面有所缓解,放开做空机制已是大势所趋。本文尝试采用统计套利的思想,利用协整模型,先在机制成熟的外汇市场进行套利检验,选取相关度较高的欧元/美元(EUR/USD)和瑞郎/日元(CHR/JPY)两个货币对在2015年5月28日20时至5月29日20时每分钟收盘价的价差时间序列进行实证研究,发现日内存在大量的套利机会,从而为今后投资者提供了一种新颖的量化投资思路。
关键词 :统计套利,高频数据,协整模型,汇市交易

1. 引言
1.1. 统计套利背景简介
尽管外汇市场早已实现了电子化交易,但套汇理论仍然处于较低的水平。Levich (2001) [1] 出版的国际金融理论前沿读本仍在使用三角套利理论作为全球套汇理论,Bolland和Connor (2000) [2] 运用卡尔曼滤波法来识别套汇机会,算法低效且繁琐。显然,以上的方法已不能满足现代汇市的要求。随着市场的不断发展,亦将有新的交易策略涌现出来。
统计套利策略诞生于上世纪八十年代的华尔街,它是一种被国外对冲基金等投资机构成功运用的策略,能在为投资者带来巨额收益的同时保持较低的风险。其原理是利用两种资产的相关性以及关系的稳定性,在价差超过一个稳定的水平时,卖空看空资产并且买入相关度较高的另一种看多资产。值得注意的是,相对于无风险套利,统计套利并非零风险,而是使用的数学模型保证长期赢利,在统计学上是大概率事件。Engle和Granger (1987) [3] 年提出了协整的思想,这为统计套利提供了重要的理论基础。
国外关于应用统计套利技术的文献相对较多,起源也相对较早,Burgess (1999) [4] 等学者经过实证研究后发现基于协整的统计套利效果明显优于其它的跟踪误差方差方法,在时效性和效率方面有很大优势。Rudy, Dunis, Giorgioni和Laws (2010) [5] 采用高频数据进行股票市场的套利,并且比较了协整关系对于套利结果的影响。结果表明,股票间价格协整关系越高,统计套利的机会也相应地增加,潜在收益率也越高。
在国内的学者中,方昊(2005) [6] 是该领域的先行者,他将统计套利的思想运用于我国的封闭式基金市场,使用10个封闭式基金日的收盘数据作为研究对象,运用协整理论设置进出场阈值为1倍标准差,止损阈值为10%,结果表明该策略有效。仇中群,程希骏(2008) [7] 用基于协整的统计套利模型在沪深300股指期货的仿真交易中进行研究,发现了市场中的跨期套利空间,证明了统计套利策略的。叶恒洁(2009) [8] 通过协整模型发现,潞安环能和西山煤电两只股票价格存在协整关系,两只股票的价差在−15%到15%之间波动。目前国内对统计套利尚处在起步阶段,采用日数据是传统统计套利的惯例,协整模型是国内外统计套利策略的传统模型。然而随着高频数据技术的兴起,日内的套利机会已经引起了投资者和研究人员的高度关注。
1.2. 分析方法
统计套利策略将套利建立在对历史数据统计分析的基础上,基本原理是假定资产的某个线性的价差是一个平稳过程,即该价差的均值和方差在长期内保持稳定,则价差将围绕均值上下波动。本文釆用的是基于协整方法的配对交易策略,建模过程包括相关性分析、平稳性分析、协整检验、ADF (Augmented Dickey-Fuller)检验、线性回归等步骤。
本文采用实证分析法,选取欧元/美元和瑞郎/日元两个货币对作为研究对象,为了使结果更加精确,使用2015年5月28日20时至5月29日20时两个货币对每分钟的高频数据作为研究样本,由于数据量较大,所以我们采用EViews软件进行分析、检验。
数据来源:GAIN Capital嘉盛外汇平台
2. 统计套利模型介绍
2.1. 模型含义概述
统计套利是一种基于金融资产价格的时间序列模型的投资过程。投资者在不依赖于经济含义的情况下,仅运用数量手段构建资产组合,根据资产组合内部金融资产价格之间的变化规律,来发现其中的套利机会,构建投资组合的多头和空头,从而对市场风险进行规避,获取一个稳定的收益率。
2.2. 统计套利不是无风险套利
统计套利是利用价格的历史统计规律进行套利,是一种风险套利,其风险在于这种历史统计规律在未来一段时间内是否持续存在。统计套利由于不能被投资者直观观测到,因此其发生的几率比无风险套利的机会高,但同时获利的机会较之无风险套利也更多。
2.3. 统计套利的数学定义
Hogan, Jarrow, Teo和Warachka (2004) [9] 对统计套利进行了精确的数学定义,他们强调统计套利是具有零初始成本、自融资的交易策略。
用V(t)表示在t时刻的累计收益,以无风险利率折现的现值为v(t),v(t)应满足:
1)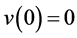 ;
;
2) ;
;
3)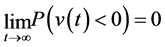 ;
;
4) 若 则
则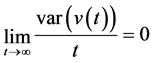 。
。
该定义表明了统计套利需要满足的四个条件:
1) 零初始成本;
2) 利润的现值为正数,统计套利有条件地向纯套利收敛;
3) 亏损的概率趋近于0 (与无风险套利的不同之处在于,无风险套利亏损的概率等于0);
4) 时间的平均方差趋近于0。
由定义我们可以看出,统计套利的基本思路简而言之,就是均值回复的原理。对一组高度相关联的价格之间的关系的历史数据进行分析,研究其在历史上的稳定性,并估计其概率的分布,确定该分布中的否定域。当真实市场上的价格关系进入否定域时,我们认为该种价格关系不可长久维持,套利者有较高成功概率进场套利。如图1所示。
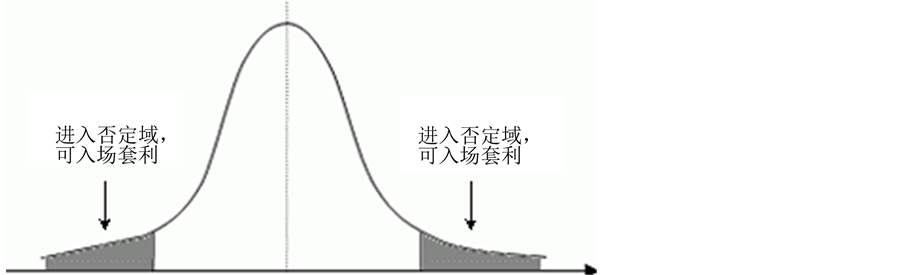
Figure 1. Curve: decision of entering the market
图1. 入场时机的选择
统计套利是只针对有稳定性的价格关系进行的,如果缺乏稳定性,套利策略将会面临很大的风险。所以在对金融资产价格关系的时间序列进行分析时,首先要检验它的平稳性。如果是稳定的,那么它必定是靠着某种机制来维持的,一旦价格关系偏离均衡水平,该机制就会起到维持作用,将价格关系以一定的速度拉回均衡水平。所以,要分析一组价格关系是否稳定,需要先定性分析是否存在着这种机制来维持均衡,然后再对历史数据进行分析验证,以证实该机制的确发挥其作用。
3. 实证分析
3.1. 选取配对货币对(相关性检验)
由于条件限制,我们随机选取八个货币对在2015年5月28日20时至5月29日20时每分钟的收盘价(欧元/美元、英镑/美元、澳元/日元、澳元/美元、瑞郎/日元、欧元/加元、欧元/瑞郎、美元/日元),每组1439个数据(数据来源:GAINcapital英国嘉盛外汇)。将其导入Eviews,保存为序列(Series)并分别命名为X1、X2... X8。建立包含该八个序列的群组(group),在群组中观察八个序列之间每两个序列的相关系数(correlation),结果如图:
结果表明欧元/美元(X1)和瑞郎/日元(X5)的相关系数最高,为0.8267,因此两个序列之间有着相对显著的相关关系,存在协整关系的可能性较高,统计套利交易的可能性也较大,所以我们选择这两个货币对作为研究对象。
3.2. 单位根的ADF (Augmented Dickey-Fuller)检验
在对欧元/美元和瑞郎/日元一分钟收盘价时间序列进行协整检验之前,我们需要先确定这两个时间序列具有相同的单整阶数,进行协整的前提条件是必须是非平稳的时间序列。
由图我们可以直观地看出,两个时间序列的均值和方差均不稳定,因此应该都是非平稳序列。为了量化地研究时间序列是否平稳,我们需要对两个变量的时间序列进行单位根检验,结果如下(采用不带趋势和截距项的单位根检验):
由于两个序列的P值都很好,因此我们有很高的概率接受原假设,即X1、X5存在单位根。为了得到X1、X5序列的单整阶数,在单位根检验指定对一阶差分序列做单位根检验,结果为:
从检验结果看,显然我们应该拒绝原假设,表明X1、X5的一阶差分序列不存在单位根,是平稳序列,即X1、X5序列是一阶单整的,X1~I(1),X5~I(1)。
3.3. 协整检验
通过ADF检验,我们得出欧元/美元(X1)和瑞郎/日元(X5)的时间序列都是一阶单整的结论,因此我们可以利用“Engle-Granger”两步法来检验两个时间序列之间是否存在协整关系,我们先做两个变量之间的回归,然后检验回归残差的平稳性。
以瑞郎/日元(X5)作为被解释变量,欧元/美元(X1)作为被解释变量,用OLS回归估计回归模型,估计的结果为:
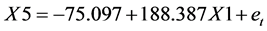

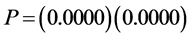
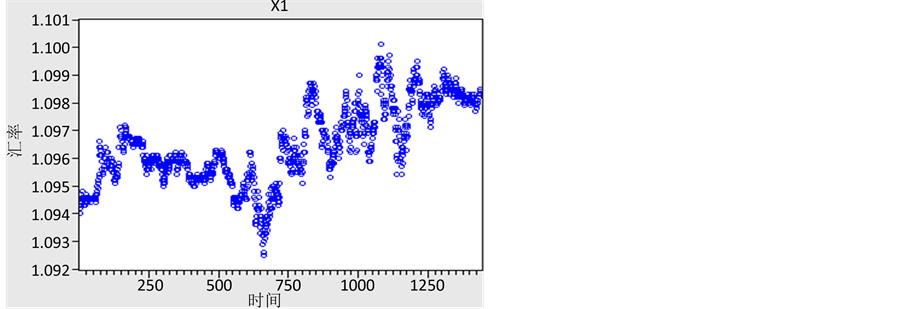
Figure 2. Scatter plot of X1
图2. X1时间序列的散点图
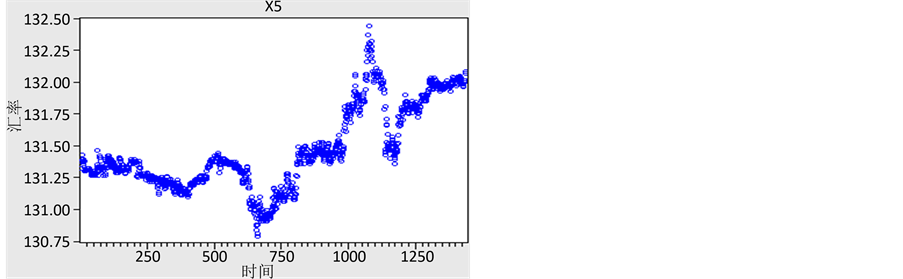
Figure 3. Scatter plot of X5
图3. X5时间序列的散点图
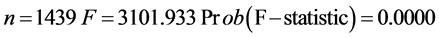
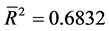
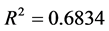
为了检验回归残差的平稳性,建立新序列et = Resid (将回归得到的残差序列命名为新序列et),然后对et序列进行单位根检验。由于残差序列的均值为0,选择无截距项、无趋势项的ADF检验,估计结果P值等于0.0062,在1%、5%、10%三个显著性水平下,MacKicnnon临界值均小于t检验统计值,从而拒绝原假设,表明残差序列不存在单位根,是平稳序列。说明欧元/美元(X1)和瑞郎/日元(X5)之间存在协整关系,即两者之间有长期均衡关系。
3.4. 套利机会检验与进场出场点设置
3.4.1. 建立交易组合
由上一步的回归方程我们得到欧元/美元(X1)和瑞郎/日元(X5)的每分钟收盘价存在如下的长期均衡关系:
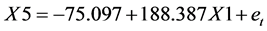
由于该种均衡关系,我们可以利用回归模型中X1的系数作为交易的对冲比例进行组合投资,如果有1单位的X5则需要188.387单位的X1进行反向对冲。
3.4.2. 确定交易信号
通过对回归方程的变形可以得到残差: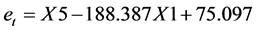 。
。
且标准差σ (standard deviation)为0.181。
用spread表示X5与X1的价差,表示为: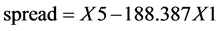 。
。
用mspread表示价差的均值。
为了便于序列数据集中化,我们对spread价差序列进行去中心化操作:
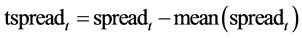 价差序列图如图4。
价差序列图如图4。
详细的点位分布如下表所示:
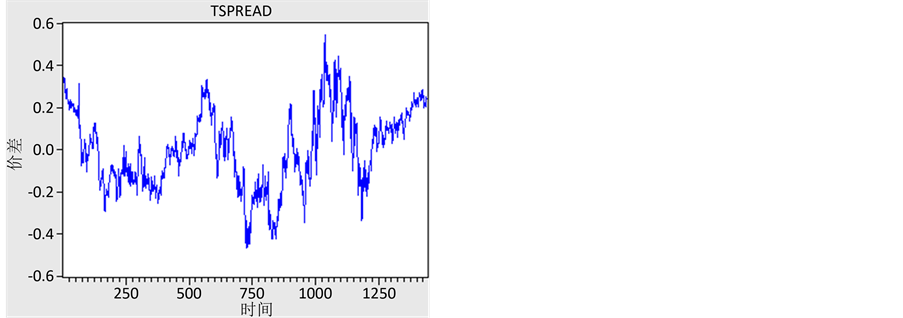
Figure 4. Price difference after decentralization
图4. 去中心化后的价差序列图
由以上图表可以看出,去中心化之后的价差序列不会持续的大于或者小于零,而是在零值附近随即波动。这与均值回复半周期较短的结论相契合,说明价差向均值回复的速度是很快的。
通过对去中心化价差序列tspread的分析可以构造合适的统计套利方案。当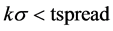 时,说明资产X5相对于X1被高估,当tspread值提高到至少覆盖所有交易所需的费用的时候,我们可以找到一个置信度很高的开仓点,在该时刻卖出X5并买进X1,当tspread回归到均衡值将二者进行平仓,这样即可获得X1的部分套利利润。
时,说明资产X5相对于X1被高估,当tspread值提高到至少覆盖所有交易所需的费用的时候,我们可以找到一个置信度很高的开仓点,在该时刻卖出X5并买进X1,当tspread回归到均衡值将二者进行平仓,这样即可获得X1的部分套利利润。
同理当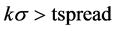 时,说明X5相对于X1被低估,tspread值偏离均值到一定程度的时候可以开仓买进X5,卖出X1,当tspread回归到均衡值时将两个资产平仓以获利。
时,说明X5相对于X1被低估,tspread值偏离均值到一定程度的时候可以开仓买进X5,卖出X1,当tspread回归到均衡值时将两个资产平仓以获利。
3.4.3. 设定建仓、平仓与止损阈值
传统套利模型需要确定进出场阈值,一般开仓阈值为价差等于价差的均值加上k倍的标准差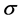 ,即
,即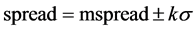 ,平仓阈值为价差等于价差的均值,即
,平仓阈值为价差等于价差的均值,即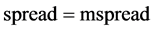 。
。
确定交易区间的建模方法有很多,Vidyamurthy (2004) [10] 在“Pairs Trading:Quantitative Methods and Analysis”一书中介绍了如ARMA模型、混合正态分布等方法,并且通过随机模拟得到以下结论:假设去均值后的价差波动是一个白噪声序列,那么最大收益的交易边界条件是±0.75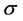 ,这比较适合作为样本内数据的设定。
,这比较适合作为样本内数据的设定。
由此我们可以得到tspread序列相应均衡的价格区间为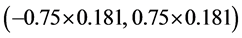 ,即
,即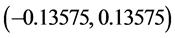 。若在t时刻价格落在该区间以外,立刻进行建仓,记此时价差为
。若在t时刻价格落在该区间以外,立刻进行建仓,记此时价差为 ,当价差在T时刻恢复至mspread时进行平仓,记此时价差为
,当价差在T时刻恢复至mspread时进行平仓,记此时价差为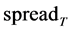 ,则单次套利收益为:
,则单次套利收益为: ,m为样本内套利次数。取2倍标准差为上下止损位,即
,m为样本内套利次数。取2倍标准差为上下止损位,即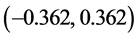 。这源于风险价值VaR的思想:假设去中心化的对数价差服从正态分布,我们有95%信心的保证其波动幅度不超过1.96 倍标准差。将以上结论的思想运用在tspread的图标中,可绘制出如图5所示的交易时机图。
。这源于风险价值VaR的思想:假设去中心化的对数价差服从正态分布,我们有95%信心的保证其波动幅度不超过1.96 倍标准差。将以上结论的思想运用在tspread的图标中,可绘制出如图5所示的交易时机图。
图中绿线为开仓位tspread = −0.13575及0.13575。
红线为止损位tspread = −0.362及0.362。
黑线为平仓位tspread = 0。
我们可以明显的看出,在2015年5月28日20时至5月29日20时一天的时间内出现了非常广泛的套利机会,且套利失败强制平仓的次数相对很少。证明利用这种统计套利策略可以有效地分散风险,并获得稳定的收益。
4. 样本外绩效检验
为了研究该模型在样本外的运行情况,我们选取2015年5月21日0时至5月22日0时每分钟两种货币对的收盘价进行检验。
对于样本外的交易策略,因为数据不在样本范围之内,因此其波动可能十分剧烈,当价差足够高才可触发交易。很多文献对开仓点设置2倍标准差,对止损点设置3倍标准差以增强安全性和便捷性,同时可以减少交易费用,在这里我们亦采用这种方法进行研究。
我们计算出开仓点为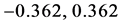 ,止损点为
,止损点为 ,平仓点为0。
,平仓点为0。
建立5月21日全天欧元/美元、瑞郎/日元每分钟收盘价格的时间序列,分别命名为X6、X7,并归于同一个群组中。依照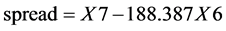 ,我们建立新的价差序列并对其进行去中心化,得到新的tspread图像(图6)。
,我们建立新的价差序列并对其进行去中心化,得到新的tspread图像(图6)。
由此可见,价差波动比较剧烈,并且在此种进出场点的设置下,样本外的统计套利在此影响下套利机会并不多,较之样本有很大程度的减少,但稳健性有所提高。
5. 不足与改进
首先为增加模型的自适应性,可以通过对模型残差项的标准差进行建模分析,设置随时间波动的阈
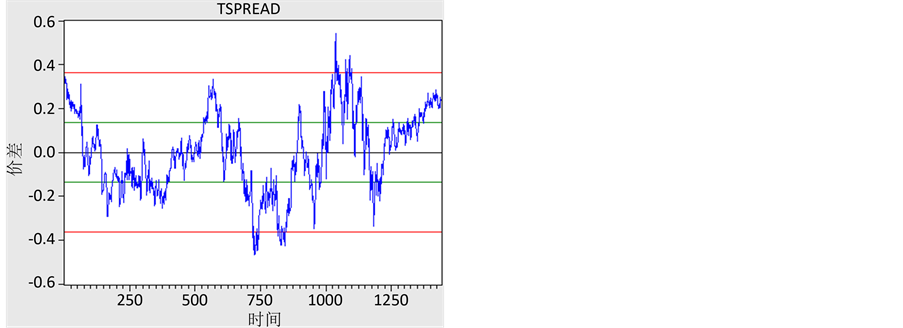
Figure 5. Trading opportunities
图5. 交易时机图
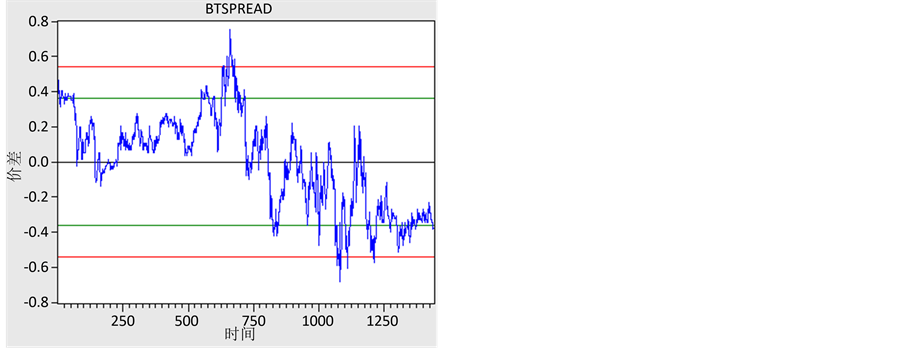
Figure 6. Efficiency test outside sample data
图6. 样本外的效果检验
值来调整进场点,优化投资策略。通过matlab可建立一套自动交易系统,精确地计算出套利次数,盈利金额以及盈利率等信息(详细套利报告),本文因条件限制未能提供。可引入夏普指数(Sharpe Ratio)的概念,将其作为指标来衡量模型的绩效,并且与其他方法进行比较。在交易对象的选取上可能会有相关度更高的资产组合,本文仅随机选取了八个货币对进行配对交易。此外,在实际情况中产生的交易摩擦本文为简化计算没有加入。
6. 总结与展望
本文运用日内每分钟收盘的高频数据,探究了存在协整关系的两个相关性较高的货币对之间存在的统计套利机会,并构建一套相应的统计套利机制。通过实证研究发现欧元/美元和瑞郎/日元两个货币对之间长期上存在协整关系,利用这种关系进行套利,通过对2015年5月28日20时至5月29日20时的样本计算价差并去中心化之后进行回测发现,当把开仓点设置为0.75个标准差,止损点为2个标准差,平仓点为0的时候,日内存在着大量的统计套利机会。当买入1单位的瑞郎/日元时可买入188.387单位的欧元/美元进行风险对冲。该种交易模式为交易者和投资机构外汇市场套利提供了一种新的思路和方法。
本文虽然是将协整的成对交易统计套利方法应用于汇市交易,但这种思想同样可以应用于有做空机制的证券市场,如股票指数期货,融资融券市场和股票期权等衍生品市场。虽然目前中国大陆股市缺乏做空机制,但随着2010年以来中国股指期货的试点运行以及融资融券政策等为资本市场提供卖空机会的利好政策的出台,中国的股票市场也将可以进行做空交易,因此我们的研究是一种前瞻性的方法,为推出做空机制后的多元操作策略提供一些有实际意义的思路。
致谢
本文在选题及研究过程中承蒙南京工业大学理学院邓晓卫教授、吕学斌副教授悉心指导,在此向两位老师致以诚挚的谢意和崇高的敬意。
文章引用
肖敦健,邓晓卫,夏冰倩. 一种基于高频数据的汇市统计套利策略
A Statistical Arbitrage Strategy in Forex Market Based on High-Frequency Data[J]. 金融, 2017, 07(01): 38-46. http://dx.doi.org/10.12677/FIN.2017.71005
参考文献 (References)
- 1. Levich, R.M. (2001) International Financial Markets. McGraw-Hill/Irwin, New York, 141-152.
- 2. Bolland, P.J. and Connor, J.T. (1998) A Robust Non-Linear Multivariate Kalman Filter for Arbitrage Identification in High Frequency Data. Neural Networks in Financial Engineering, 122-135.
- 3. Engle, R.F. and Granger, C.W.J. (1987) Co-Integration and Error Correction: Representation, Estimation, and Testing. Econometrica, 55, 251-276. https://doi.org/10.2307/1913236
- 4. Burgess, N. (2000) Statistical Arbitrage Models of the FTSE 100. Computational Finance, The MIT Press, Cambridge, 297-312.
- 5. Rudy, J., Dunis, C., Giorgioni, G. and Laws, J. (2010) Statistical Arbitrage and High-Frequency Data with an Application to Eurostoxx 50 Equities. Social Science Electronic Publishing, Rochester.
- 6. 方昊. 统计套利的理论模式及应用分析: 基于中国封闭式基金市场的检验[J]. 统计与决策, 2005(12): 14-16.
- 7. 仇中群, 程希骏. 基于协整的股指期货跨期套利模型[J]. 系统工程, 2008(12): 26-29.
- 8. 叶恒洁. 基于协整的统计套利实证研究[J]. 中国商贸, 2009(13): 238-238.
- 9. Hogan, S., Jarrow, R., Teo, M. and Warachka, M. (2004) Testing Market Efficiency Using Statistical Arbitrage with Applications to Momentum and Value Strategies. Journal of Financial Economics, 73, 525-565. https://doi.org/10.1016/j.jfineco.2003.10.004
- 10. Vidyamurthy, G. (2004) Pairs Trading: Quantitative Methods and Analysis. Pearson Schweiz Ag, Zug, 35-47.