Pure Mathematics
Vol.06 No.04(2016), Article ID:18114,10
pages
10.12677/PM.2016.64048
The Oscillation of the Linear Functional Equations
Lina Dai, Yanfen Xu*, Quanwen Lin
Department of Mathematics, Science of School, Guangdong University of Petrochemical Technology, Maoming Guangdong

Received: Jul. 9th, 2016; accepted: Jul. 24th, 2016; published: Jul. 28th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we study of oscillatory of all solutions to the high order equation
 We get some new vibration conditions, and improve or promote some of the results of previous literature.
We get some new vibration conditions, and improve or promote some of the results of previous literature.
Keywords:Functional Equations, Solutions, Oscillation, Non-Oscillation

线性泛函方程解的振动性
戴丽娜,徐艳芬*,林全文
广东石油化工学院理学院数学系,广东 茂名

收稿日期:2016年7月9日;录用日期:2016年7月24日;发布日期:2016年7月28日

摘 要
本文研究高阶泛函方程

解的振动性,得到了一些新的振动条件,改进或推广已有文献的某些结果。
关键词 :泛函方程,解,振动性,非振动性

1. 引言
考虑高阶线性泛函方程
 ,
,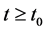 (1.1)
(1.1)
其中 :
: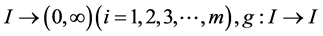 是给定的函数,
是给定的函数,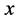 是未知实值函数,
是未知实值函数,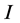 是
是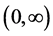 上的一个无界子集,
上的一个无界子集,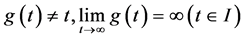 。
。 表示函数
表示函数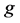 的
的 次迭代,即
次迭代,即
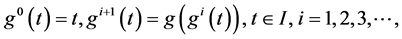
如果函数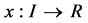 使得
使得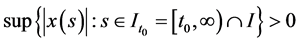 对任何
对任何 成立,且对
成立,且对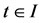 满足(1.1),则称其为方程(1.1)的一个解。这样的解称作是振动的。如果存在一列点
满足(1.1),则称其为方程(1.1)的一个解。这样的解称作是振动的。如果存在一列点 ,使得
,使得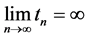 ,且
,且 对
对 成立。否则称为非振动的。
成立。否则称为非振动的。
当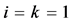 时,可得出文 [1] 泛函方程
时,可得出文 [1] 泛函方程
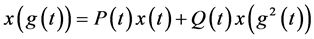 (1.2)
(1.2)
其中 是给定的函数。
是给定的函数。
1995年,在文 [2] Nowakowska和Werbowski将方程(1.2)推广高阶线性泛函方程(1.1)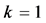 的情形,得到方程(1.1)的所有解振动,如果
的情形,得到方程(1.1)的所有解振动,如果
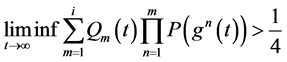 (1.3)
(1.3)
或
 (1.4)
(1.4)
其中
 (1.5)
(1.5)
1998年以来,函数方程的振动性成为数学工作者研究研究的热门课题他们得到各类线性高级泛函方程和非线性高阶泛函方程解的振动准则(请参看文 [3] - [12] ) (从略)。
2003年,文 [7] 研究了方程(1.1)的一种特殊形式
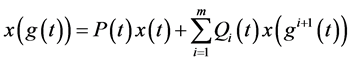 (1.6)
(1.6)
(i) 如果下面条件之一成立:

或

其中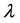 是
是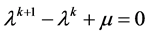 在[0,1]上最大实根。则泛函方程(1.6)的所有解振动。
在[0,1]上最大实根。则泛函方程(1.6)的所有解振动。
(ii) 如果下面条件之一成立
(1) 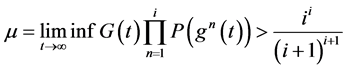
(2) (1.7)
(1.7)
其中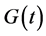 由文 [7] (1.7)定义而
由文 [7] (1.7)定义而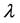 和
和 分别由引理2.1和引理2.2确定。则泛函方程(1.6)的所有解振动。
分别由引理2.1和引理2.2确定。则泛函方程(1.6)的所有解振动。
(iii)如果下面条件之一成立
(1)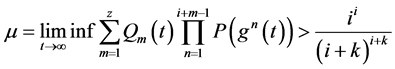 ,
,
(2) (1.8)
(1.8)
其中 和
和 分别由文 [7] 引理2.1和引理2.2确定。则泛函方程(1.6)的所有解振动。
分别由文 [7] 引理2.1和引理2.2确定。则泛函方程(1.6)的所有解振动。
显然,当 ,方程(1.1)变为方程(1.6)。本文在文 [7] 基础上,利用新的技巧进一步研究(1.1),得到若干振动准则,我们的结果推广了文 [7] 的结果,改进了文 [1] , [2] 的某些结果。
,方程(1.1)变为方程(1.6)。本文在文 [7] 基础上,利用新的技巧进一步研究(1.1),得到若干振动准则,我们的结果推广了文 [7] 的结果,改进了文 [1] , [2] 的某些结果。
2. 引理
考虑泛函不等式
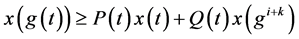 (2.1)
(2.1)
并令

在证明定理之前,为了简明首先证明以下引理。
引理2.1:假设 ,
,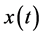 是泛函不等式(2.1)的一个最终正解,那么
是泛函不等式(2.1)的一个最终正解,那么
 (2.2)
(2.2)
这里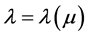 是方程
是方程
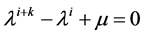
在[0,1]上的最大实根。
证:从(2.1)容易看出
 (2.3)
(2.3)
由于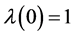 ,所以当
,所以当 时(2.2)成立。现在假设
时(2.2)成立。现在假设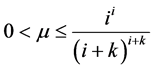 ,那么对任何
,那么对任何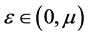 和足够大的
和足够大的 ,由
,由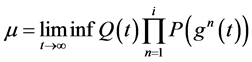 ,得:
,得:
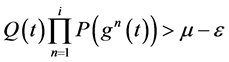 (2.4)
(2.4)
由(2.3),有

迭代1次,有:

迭代2次,有:
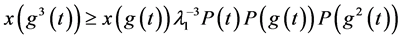
迭代3次,有:

根据数学归纳法,迭代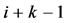 次,有:
次,有:
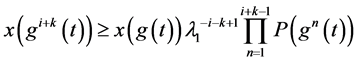
将上式代入(2.1),并利用(2.4)得

以上不等式除以 ,只考虑不等式最左端与最右端,有:
,只考虑不等式最左端与最右端,有:

有:

重复上面的推导,由归纳法,得
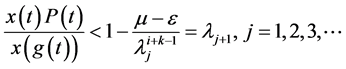
显然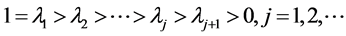 ,此函数单调递减且有界,所以
,此函数单调递减且有界,所以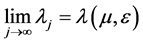 存在,
存在,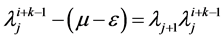 ,通过移项,令j趋于无穷,有:
,通过移项,令j趋于无穷,有:
 ,
,
于是
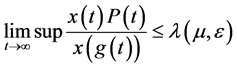
令 ,注意到
,注意到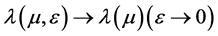 ,从上式我们得到(2.2)。引理证毕。
,从上式我们得到(2.2)。引理证毕。
本文引理2.1通过利用极限的思想及方程根存在性,推广了文 [7] 引理2.1原有的结果所需的条件,当k = 1时,正是文 [7] 引理2.1的条件。所以说,本文中的条件比文 [7] 条件适用范围更广,结果更具有一般性。
引理2.2:假设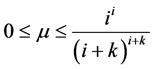 ,
, 是泛函不等式(2.1)的一个最终正解,那么
是泛函不等式(2.1)的一个最终正解,那么
 (2.5)
(2.5)
这里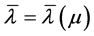 是方程
是方程
 (2.6)
(2.6)
在[0,1]上的最小实根,而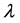 由引理2.1确定。
由引理2.1确定。
证: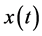 是不等式(2.1)的最终正解,所以最终
是不等式(2.1)的最终正解,所以最终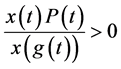 。由于
。由于 ,故当
,故当 时(2.5)成立。现在假设
时(2.5)成立。现在假设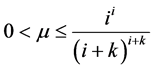 ,那么对任何
,那么对任何 和足够大的
和足够大的 ,(2.4)成立,且
,(2.4)成立,且
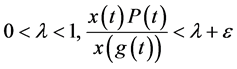 (2.7)
(2.7)
由(2.1),令 ,有:
,有:
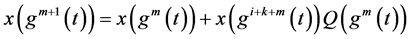
等式两边同乘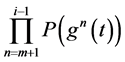 有:
有:
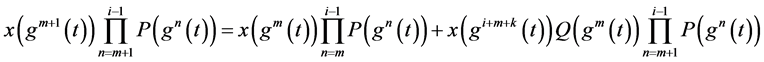 (2.8)
(2.8)
对(2.8)从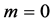 到
到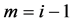 作和,得
作和,得
 (2.9)
(2.9)
由(2.4),(2.7)和(2.9)得
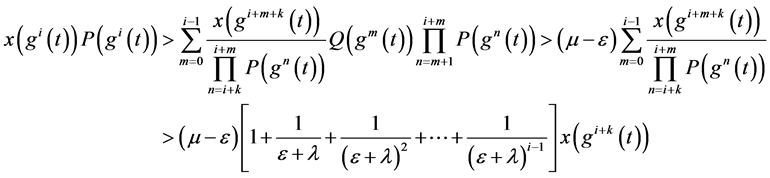
所以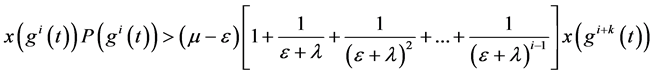 ,有:
,有:
 (2.10)
(2.10)
由(2.4),(2.7),(2.9)和(2.10)有
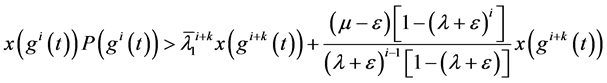
因此等式两边同时除以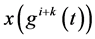 得:
得:

重复上面的推导,由归纳法,我们得:

容易看出, ,此函数列单调递减且有界,所以极限
,此函数列单调递减且有界,所以极限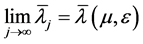 存在,令
存在,令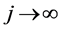 满足
满足
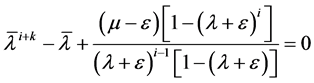 (2.11)
(2.11)
于是

令 ,我们得(2.8)。利用引理2.1和(2.11)(令
,我们得(2.8)。利用引理2.1和(2.11)(令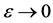 ),易得
),易得 满足(2.9)。引理证毕。
满足(2.9)。引理证毕。
本文引理2.2通过利用极限的思想及方程根存在性,推广了文 [7] 引理2.2原有的结果所需的条件,当k = 1时,正是文 [7] 引理2.2的条件。所以说,本文中的条件比文 [7] 条件适用范围更广,结果更具有一般性。
引理2.3:如果下面条件之一成立
(1)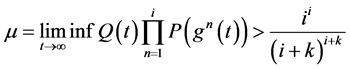 (2.12)
(2.12)
(2)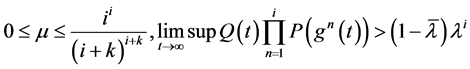 (2.13)
(2.13)
其中 和
和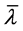 分别由引理2.1和引理2.2确定。则泛函不等式(2.1)无最终正解。
分别由引理2.1和引理2.2确定。则泛函不等式(2.1)无最终正解。
证:如果(1)成立,由于

由 [2] 中引理1,不等式(2.1)无最终正解。引理前半部分得证。
为了证明引理的后半部分,我们假设(2.1)有最终正解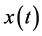 。那么。由(2.1)
。那么。由(2.1)
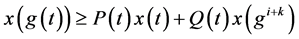
有

所以
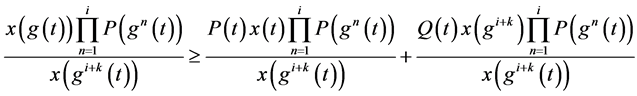
所以

取上极限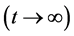 并利用引理2.1和引理2.2得
并利用引理2.1和引理2.2得
 。
。
这与(2.13)矛盾。所以引理的后半部分得证。引理证毕。
本文引理2.1通过利用极限的思想及方程根存在性,推广了文 [7] 引理2.1原有的结果所需的条件,当k = 1时,正是文 [7] 引理2.1的条件。所以说,本文中的条件比文 [7] 条件适用范围更广,结果更具有一般性。
3. 结果及证明
首先,由引理2.3立即得
定理3.1:如果下面条件之一成立
(1) (3.1)
(3.1)
(2)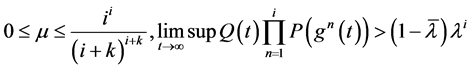 (3.2)
(3.2)
其中 和
和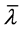 分别由引理2.1和引理2.2确定。则泛函方程
分别由引理2.1和引理2.2确定。则泛函方程
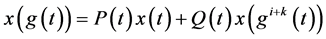 (3.3)
(3.3)
的所有解振动。
当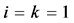 时,容易得到
时,容易得到

本文定理3.1通过运用文中以推广的引理结果,推广了文 [7] 定理3.1,显然当k = 1为文 [7] 定理3.1即本文(1.6)中的情况,所以说,本文得到的振动性需要的条件更优。
所以,由定理3.1我们有如下推论
推论3.1:如果下面条件之一成立
(1)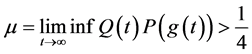 (3.4)
(3.4)
(2)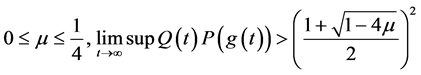 (3.5)
(3.5)
则泛函方程(1.2)所有解振动。
定理3.2:如果下面条件之一成立
(1)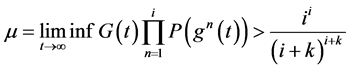 (3,6)
(3,6)
(2) (3.7)
(3.7)
其中 由(1.5)定义而
由(1.5)定义而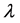 和
和 分别由引理2.1和引理2.2确定。则泛函方程(1.1)的所有解振动。
分别由引理2.1和引理2.2确定。则泛函方程(1.1)的所有解振动。
证:假设(1.1)有最终正解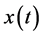 。那么,由(1.1)有
。那么,由(1.1)有

令 有
有 ,
, ,有:
,有:
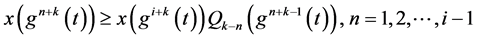
将上式代入(1.1)并注意到(1.7)得
 (3.8)
(3.8)
由引理2.3,不等式(3.8)无最终正解,这是一个矛盾。定理得证。
本文定理3.2运用本文以推广的引理,推广了文 [7] 定理3.2,显然当k = 1为文 [7] 定理3.2即本文(1.7)中的情况,所以说,本文对比于文 [7] 得到的振动性需要的限制条件更少,结论更优。
定理3.3:如果下面条件之一成立
(1)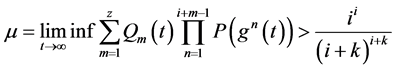 , (3.9)
, (3.9)
(2)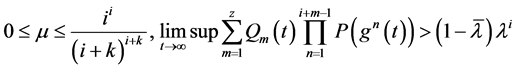 , (3.10)
, (3.10)
其中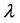 和
和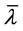 分别由引理2.1和引理2.2确定。则泛函方程(1.6)的所有解振动。
分别由引理2.1和引理2.2确定。则泛函方程(1.6)的所有解振动。
证:假设(1.6)有最终正解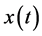 ,那么,由(1.6)有
,那么,由(1.6)有
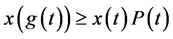
所以,对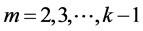 有:
有:
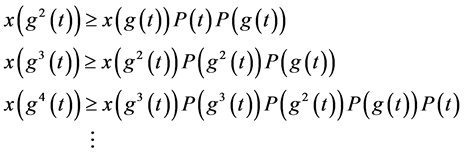
所以:
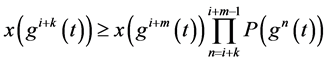 (3.11)
(3.11)
将(3.11)代入(1.6)得
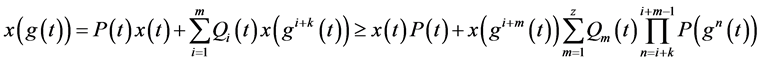 (3.12)
(3.12)
如果条件(3.9)或(3.10)成立,则由引理2.3,不等式(3.12)无最终正解,这是一个矛盾。定理得证。
本文定理3.3推广了文 [7] 定理3.1,显然当k = 1为文 [7] 定理3.3即本文(1.8)中的情况,所以说,本文对比于文 [7] 得到的振动性需要的条件更优。
在定理3.3中令 ,再用
,再用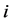 代替
代替 ,有:
,有:
推论3.2:如果下面条件之一成立
(1)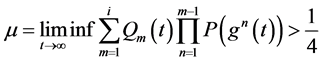 (3.13)
(3.13)
(2) (3.14)
(3.14)
则泛函方程(1.1)的所有解振动。
基金项目
国家自然科学基金(No.11271380);茂名市科技局软科学项目(No.2014083; 650306)。
文章引用
戴丽娜,徐艳芬,林全文. 线性泛函方程解的振动性
The Oscillation of the Linear Functional Equations[J]. 理论数学, 2016, 06(04): 327-336. http://dx.doi.org/10.12677/PM.2016.64048
参考文献 (References)
- 1. Golde, W. and Werbowski, J. (1994) Oscillation of Linear Functional Equations of the Second Order. Funkcialaj Ekvacioj, 37, 221-227.
- 2. Nowakowska, W. and Werbowski, J. (1995) Oscillation of Linear Functional Equations of Higher Order. Archivum Mathematicum, 31, 251-258.
- 3. Zhang, B.G., Yan, J. and Choi, S.K. (1998) Oscillation for Difference Equations with Continuous Variable. Computers & Mathematics with Applications, 36, 11-18. http://dx.doi.org/10.1016/s0898-1221(98)00189-8
- 4. Zhang, Y. and Yan, J. (1995) Oscillation Criteria for Difference Equations with Continuous Arguments, Acta Mathematica Sinica, 38, 405-411 (in Chinese).
- 5. Shen, J.H. and Stavroulakis, I.P. (2002) An Oscillation Criteria for Second Order Functional Equations. Acta Mathematica Scientia, 22, 56-62.
- 6. Shen, J.H. (1996) Comparison Theorems for the Oscillation of Difference Equations with Continuous Arguments and Applications. Chinese Science Bulletin, 41, 1506-1510.
- 7. 罗治国, 申建华. 线性泛函方程解的振动性的新结果[J]. 系统科学与数学, 2003(4): 508-516.
- 8. 周勇, 俞元洪. 变系数函数方程解的振动性[J]. 系统科学与数学, 1999, 19(3): 348-352.
- 9. 林全文, 吴英柱, 廖思泉. 泛函方程解的振动准则的一个新结果[J]. 茂名学院学报, 2009, 19(6): 58-60.
- 10. 戴丽娜. 一类函数方程的振动准则[J]. 广东石油化工学院学报, 2012, 22(4): 79-81.
- 11. 戴丽娜, 伍思敏, 林全文. 高阶变系数泛函方程的振动性[J]. 数学的实践与认识, 2014(10): 271-275.
- 12. 伍思敏, 戴丽娜, 林全文. 高阶泛函方程解的非振动准则[J]. 数学的实践与认识, 2013, 43(20): 280-285.