Pure Mathematics
Vol.07 No.04(2017), Article ID:21263,9
pages
10.12677/PM.2017.74031
The Proof of 2n Circle Arrangement Conjecture
Zuodong Wang
Beijing University of Technology, Beijing

Received: Jun. 15th, 2017; accepted: Jun. 29th, 2017; published: Jul. 6th, 2017

ABSTRACT
In this paper, I use mathematical induction and the necessary and sufficient conditions of bijection to prove the correctness of 2n circle arrangement conjecture in combinatorial mathematics.
Keywords:Combinatorial Mathematics, Circle Arrangement, Mathematical Induction, Permutation without Repetition
2n圆排列猜想证明
王作栋
北京工业大学,北京
收稿日期:2017年6月15日;录用日期:2017年6月29日;发布日期:2017年7月6日

摘 要
本文通过运用数学归纳法和两集合双射的充要条件证明了组合数学中圆排列问题下的2n圆排列猜想的正确性。
关键词 :组合数学,圆排列,数学归纳法,无重复排列

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
2n圆排列猜想是一个从中国古代河图洛书 [1] 演变推广而来的猜想。对该猜想的研究有助于完善排列组合分支下的圆排列问题,对于应用组合数学的科学领域也有贡献。本文从2n圆排列的n较小的情况入手,观察其排列规律,总结出排列方法,拆分命题,用计算机模拟计算出大量数据,并用归纳法和集合双射的充要条件证明该猜想。
2. 猜想来源
作者在大一上学期的新生研讨课(数学文化选讲)上从阴东升老师的授课中得知了老师早年在博士后研究工作报告 [2] 中提出的2n圆排列猜想。该猜想从洛书九宫图出发(图1),把洛书中各个元素都减去5,得到新的元素并适当调整次序排列在圆周上,得到下图2:

Figure 1. Lo Shu Square
图1. 洛书九宫图

Figure 2. An example of 2n circle arrangement conjecture
图2. 一个2n圆排列猜想的例子
可从图中直观看出左下角三个元素和为2,其余首尾相连的三个元素和为0。于是归纳猜想是否对于任意的大于等于2的正整数n,其从1到2n的自然数排在圆周上,适当赋予正负号,也可以得出左下角三个元素和为2,其余首尾相连的三个元素和为0的结论也成立。
3. 猜想的定义、代数描述及规律总结
3.1. 猜想定义
对于任意大于等于2的正整数n,把1到2n的自然数排在一个圆周上,人为定义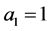 ,适当调整排列次序并赋予每个数正负号及序号(即按顺时针排,第二个数为
,适当调整排列次序并赋予每个数正负号及序号(即按顺时针排,第二个数为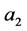 ,第三个数为
,第三个数为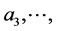 第2n个数为
第2n个数为 ),可以使得第一个数到第三个和为2;第三个数到第五个个数的和为0,第五个数到第七个数的和为0,以此类推,直到第
),可以使得第一个数到第三个和为2;第三个数到第五个个数的和为0,第五个数到第七个数的和为0,以此类推,直到第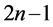 个数到第一个数的和都为0。
个数到第一个数的和都为0。
3.2. 猜想的代数描述
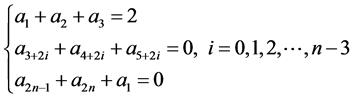
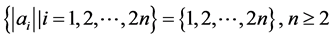
3.3. 规律总结
通过枚举的方法找出n = 2, 3, 4, 5, 6时满足原命题的情况,得到如下表1:
观察每一行与下一行的变化,总结并提出一种规律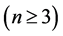 ,其作用在第n行数上时,每个数在第n + 1行会发生如下变化:
,其作用在第n行数上时,每个数在第n + 1行会发生如下变化:
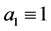 ;
;
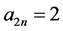 ;
;
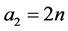 ;
;
第n行的第三个到倒数第二个数都对应第n + 1行的数,按照“减二,加一,加一,加一”的规律重复运算;
在最后增加两个数,其数值大小为:
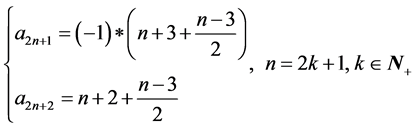
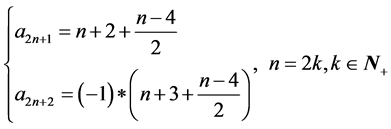
于是根据规律提出假设:
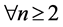 ,根据规律的发生变化后,每行数能使命题成立。
,根据规律的发生变化后,每行数能使命题成立。
Table 1. Some examples of 2n circle arrangement conjecture
表1. 一些使2n圆排列猜想成立的例子
4. 证明思路
先用计算机模拟出大量数据,再通过数学归纳法及两集合双射的充要条件进行证明。
5. 证明过程
先将原命题分解为两个命题:
命题α:
命题β: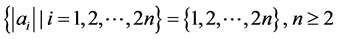
5.1. 计算机模拟过程
在Devcpp5.9.2中给出 的各个
的各个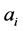 的值,把规律编进程序,循环作用后判断并输出每一次的结果(程序见附录)。
的值,把规律编进程序,循环作用后判断并输出每一次的结果(程序见附录)。
5.2. α证明过程
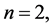
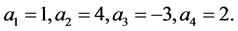

所以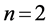 时,α成立。
时,α成立。
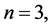
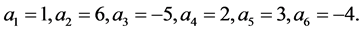
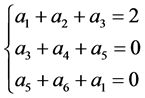
所以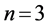 时,α成立。
时,α成立。
下证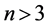 的情况:
的情况:
假设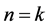 时,α成立,即
时,α成立,即 可使α成立。
可使α成立。
设在第k行的各个数根据规律发生变化后在第k + 1行分别为
1) k为奇数:
显然,
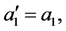
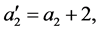
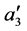 到
到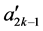 在
在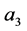 到
到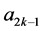 的基础上按照“减二,加一,加一,加一”的规律重复运算;
的基础上按照“减二,加一,加一,加一”的规律重复运算;
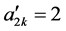
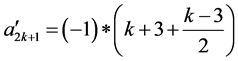

于是按照命题α的要求,对所有数进行运算可得:
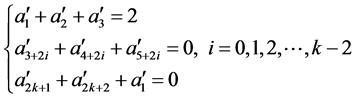
所以n为奇数时,命题α成立
2) k为偶数:
显然,


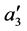 到
到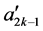 在
在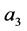 到
到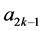 的基础上按照“减二,加一,加一,加一”的规律运算;
的基础上按照“减二,加一,加一,加一”的规律运算;
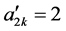
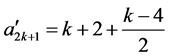
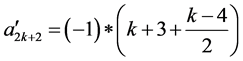
于是按照命题α的要求,对所有数进行加法运算可得:
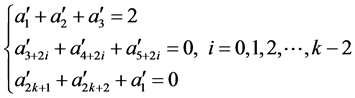
所以n为偶数时,命题α成立
所以 时,命题α成立,即根据数学归纳法命题α得证。
时,命题α成立,即根据数学归纳法命题α得证。
5.3. β证明过程

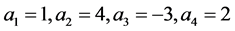
⇒ 可取尽1到2n所有的自然数。
可取尽1到2n所有的自然数。
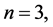
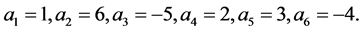
⇒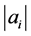 可取尽1到2n所有的自然数。
可取尽1到2n所有的自然数。
下证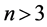 的情况:
的情况:
对于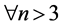 ,根据规律对
,根据规律对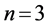 时的各个数字处理
时的各个数字处理 次可得:
次可得:
对于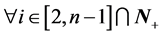 ,
,
当i为奇数时,有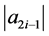 在第i行时的值为:
在第i行时的值为:
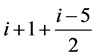
在第n行时的值为:
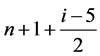
当i为偶数时,有 在第i行时的值为:
在第i行时的值为:
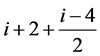
在第n行时的值为:
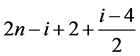
对于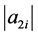 ,无论奇偶,其在下一行都变为2,在第n行变为:
,无论奇偶,其在下一行都变为2,在第n行变为:
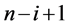
而在最后一次根据规律处理数字后有:
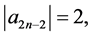
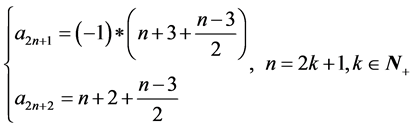
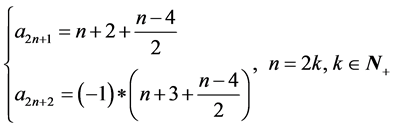
故可以得出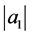 到
到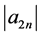 的所有值。
的所有值。
令集合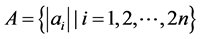 ,集合
,集合
若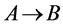 是双射,则集合
是双射,则集合 与集合
与集合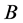 的元素一一对应,命题β成立。
的元素一一对应,命题β成立。
5.3.1. 单射证明
对于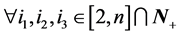 且
且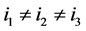 有:
有:
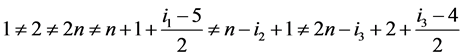
即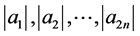 互不相等,故
互不相等,故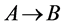 是单射。
是单射。
5.3.2. 满射证明
下证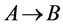 是满射:
是满射:
首先有:

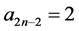
再寻找3到2n的自然数:
1) n为奇数:
把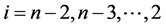 代入
代入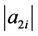 可得3到
可得3到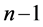 所有自然数。
所有自然数。
把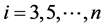 代入
代入 (奇数表达式)可得 到
(奇数表达式)可得 到 之间所有自然数。
之间所有自然数。
而 ;
;
把 代入
代入 (偶数表达式)可得
(偶数表达式)可得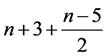 到
到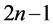 之间所有自然数。
之间所有自然数。
而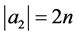
所以n为奇数时, 是满射。
是满射。
2) n为偶数:
把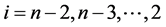 代入
代入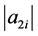 可得3到
可得3到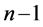 所有自然数。
所有自然数。
把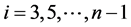 代入
代入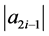 (奇数表达式)可得
(奇数表达式)可得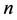 到
到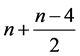 之间所有自然数。
之间所有自然数。
而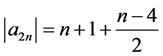
把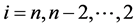 代入
代入 (偶数表达式)可得
(偶数表达式)可得 到
到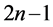 之间所有自然数。
之间所有自然数。
而
所以n为偶数时,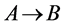 是满射。
是满射。
所以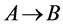 是双射。
是双射。
故集合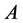 与集合
与集合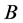 的元素一一对应,命题β成立。
的元素一一对应,命题β成立。
致谢
感谢阴东升老师在整个论文创作的过程中给予我的帮助以及传授给我数学思想及学习方法!感谢《理论数学》的审稿老师们对论文提出宝贵的修改意见!
文章引用
王作栋. 2n圆排列猜想证明
The Proof of 2n Circle Arrangement Conjecture[J]. 理论数学, 2017, 07(04): 241-249. http://dx.doi.org/10.12677/PM.2017.74031
参考文献 (References)
- 1. H. J. 赖瑟. 组合数学. 北京: 科学出版社, 1983.
- 2. 阴东升. 始向量方法及其应用[R]: [博士后研究工作报告]. 北京: 北京师范大学, 2002.5.
附录


