Pure Mathematics
Vol.08 No.03(2018), Article ID:24944,9
pages
10.12677/PM.2018.83028
A Stochastic Sub-Gradient Mirror Descent Algorithm for Non-Smooth and Strongly Convex Functions
Qian Zhou, Xianbing Luo*, Xin Wang
School of Mathematics and Statistics, Guizhou University, Guiyang Guizhou
Received: Apr. 27th, 2018; accepted: May 11th, 2018; published: May 18th, 2018

ABSTRACT
Mirror descent (MD) has been widely used to deal with the machine learning problems. For large scale data processing and non-smooth loss convex optimization problem, we proposed an improved mirror descent method, which is called modified stochastic sub-gradient mirror descent method. It combined an iterative average method with stochastic sub-gradient descent method. In the process of weighted average, the average iteration is not used to construct the algorithm, but occurs as a byproduct of our algorithm. The average weight is determined by the step size used by the algorithm. Our algorithm has good convergence. For strong convex functions, we show that the optimal convergence rate of the algorithm arrives at .
Keywords:Mirror Descent Method, Non-Smooth Loss Convex Optimization, Stochastic Sub-Gradient Mirror Descent Method, Iterative Weighted Average

一种非光滑强凸函数的随机次梯度 镜面下降算法
周倩,罗贤兵*,王鑫
贵州大学数学与统计学院,贵州 贵阳

收稿日期:2018年4月27日;录用日期:2018年5月11日;发布日期:2018年5月18日

摘 要
镜面下降法(MD)在机器学习问题中已有些实际应用,针对大规模数据的处理和非光滑损失凸优化问题,本文将迭代平均与随机次梯度镜面下降方法相结合,得到了一种改进的方法,通过对问题域的特殊处理,利用它们的结构,提出一种加权平均的随机次梯度镜面下降算法。在这个加权平均过程中,平均迭代不用于构造算法,而是作为算法的副产品出现,其中平均权重由算法使用的步长确定。该算法有很好的收敛性。对于强凸函数,我们证明了该算法的最佳收敛速度达到 。
关键词 :镜面下降法,非光滑损失凸优化,随机次梯度镜面下降法,迭代加权平均

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着机器学习的火热发展,机器学习中的大规模优化问题成为近年来被广泛研究的热门问题之一,大部分的机器学习问题的本质都是建立优化模型,通过最优化方法对目标函数(或损失函数)进行优化,从而训练出最好的模型。其主要模式是通过优化经验损失函数,模拟出最优参数,从而获得损失最小化模型 。正则化损失最小化问题是机器学习问题的常见范例,在当今机器学习的应用和研究中占主导地,强凸不可微优化问题作为正则化随机学习问题在机器学习中最为突出。大规模非光滑凸优化是机器学习和计算机虚拟等计算领域中的一个常见问题。这些领域的问题包括特殊的领域结构和特征。对这些问题域的特殊处理,利用它们的结构,可以大大提高计算效率。
众所周知,在低迭代次数下,凸优化问题可以用内点法在多对数时间内求解。然而,这些方法中的大多数都不能很好地适应优化问题的维数。内点法的单次迭代代价随问题的大小呈非线性增长。一阶方法计算上廉价的迭代成为大规模优化问题的一个可行的选择。本文提出了一种求解凸集笛卡儿乘积上一般大规模非光滑强凸优化问题的一阶自适应方法 [1] 。
我们主要关注于求解一个形式如下的优化问题:考虑约束集 上的凸函数F的最小化问题(其中F不一定是可微函数):
. (1)
设约束集 是闭凸集,函数 是凸的,且在任意点 是连续的。此外,对任意的 ,函数 的次梯度 存在,即,对任意的 ,存在向量 ,使得:
,对任意的
2. 基本的镜面下降算法
镜面下降算法 [2] [3] 是投影次梯度法 [4] 的推广。标准次梯度法在投影步长上采用欧氏距离函数,选用适当步长。镜面下降算法在非线性投影步长中,采用具有最佳步长的非线性距离函数,对标准投影次梯度法进行扩展。在这一部分中,我们回顾一个基本的镜面下降算法来解决问题(1),不考虑区域几何。
设 表示集合 中任意两点的Bregman距离函数,一个基本的镜面下降算法使用了一个非线性投影序列:
.
其中, 是函数F在点 处的次梯度, 为迭代步长。
MD方法要求距离函数的范数满足如下性质 [5] [6] :
1) 空间E上的范数 嵌入于 ,且 上的对偶范数 满足:
;
2) 集合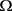 上的距离生成函数及范数
,即有连续凸函数
使得:
上的距离生成函数及范数
,即有连续凸函数
使得:
- 存在 的一个次梯度 ,在集合 上连续;
- 关于1范数 是强凸的:
.
设最大距离为 ,假设 在集合 上是Lipschitz连续的,Lipschitz常数为 ,MD方法有如下收敛性:
定理1:设 记为目标函数的全局最优解, 。选取最优步长为 ,则k次迭代的最优界为:
.
上述定理的证明参考 [1] 。
3. 随机镜面下降算法
在这一节中,我们假设问题(1)的目标函数F具有强凸性,且设其强凸系数为 ,则有:
, 对任意
接下来,我们考虑求解问题(1)的随机次梯度镜面下降算法。首先给出Bregman距离函数 [7] 的定义如下:
设 为集合 上连续可微的强凸函数,即存在 ,使得
, 对任意 (2)
则由函数 生成的Bregman距离函数记为 定义为:
, 对任意 (3)
从定义可以看出,Bregman距离函数具有以下性质:
, 对任意 (4)
, 对任意 (5)
上述性质都可由函数 的强凸性质得到。又函数 连续可微,可知函数 关于u可微,设 表示 关于u的偏导数,则有:
。对任意 (6)
设 为初始点,则问题(1)的次梯度镜面下降法的迭代公式如下:
, 对任意
其中 为迭代步长, 为函数 在点 的次梯度。当集合 具有的结构能允许对 有效计算的前提下,该算法有效,例如, 的闭形式是有效的。为了处理更一般的形式,我们采用随机思想,用目标函数次梯度的无偏估计代替其次梯度。即用任意选取的某一个损失函数 的次梯度 代替目标函数 的次梯度,从而得到如下形式的随机次梯度镜面下降算法:
, 对任意 (7)
其中任意选取初始点 ,满足 ,但是与随机次梯度序列 无关。
迭代步长 ,设其满足
, 对任意 , . (8)
为了使上述假设看起来更有意义,我们讨论步长的选取问题。由设定的步长条件(8),我们有:
, 对任意
初始化 。我们将考虑下面两种特殊的步长选择:
和 , 对任意 (9)
上述的第一个步长由Tseng [8] 提出,设第二个式子中
,则得到Nesterov序列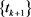 [9] ,它用于构造梯度Lipschitz连续的凸函数的快速一阶算法,即
[9] ,它用于构造梯度Lipschitz连续的凸函数的快速一阶算法,即
, 对任意
且 [10] 。通过归纳,我们可以发现 ,对任意 ,从而推出(9)中的两个步长公式都满足:
, 对任意 , 且
由于步长 满足(8),则有
, 对任意 .
我们可以建立基本的随机次梯度镜面下降算法如下:
a) 任意选取初始点 ,满足 ,一般我们选取 。
b) 。
c) 。
这里,我们取 ,且 。观察发现,上述迭代中,每次循环都需存储 ,加权平均值 ,以及步长的相关和 。
我们假设 ,其中 ,这样我们可以将上述c改成:
.
这也就是我们说的加权平均迭代的随机次梯度镜面下降算法。
4. 算法的收敛性分析
接下来,我们对算法的收敛性进行理论分析。首先,讨论步长满足条件(8)的随机次梯度镜面下降法的迭代特点。这里我们假设Bregman距离函数满足如下要求:
, 对任意 (10)
上述关系成立,当Bregman距离生成函数 在集合 上梯度Lipschitz连续,且Lipschitz参数 ,即,
, 对任意
观察发现,基于函数 的梯度Lipschitz连续的性质,则对任意 ,我们有
,
其中后面的不等式可由函数 在 上的凸性得到。而且,若 在 上满足梯度Lipschitz连续,且Lipschitz常数为 ,
, 对任意
则存在函数 ,其梯度的Lipschitz常数为 。这样的函数可以用做满足式(10)的距离生成函数。对于欧式空间,我们取 ,得Bregman距离函数为 ,同样满足式(10)。
假设1:设随机次梯度 满足 ,对任意 ,则存在某一标量 使得对任意 ,有 。
当 时,假设1中次梯度在 上一致有界,即存在 使得对任意 ,有 。若目标函数的次梯度一致有界,且满足 ,存在某个 ,使得对任意 , ,则对于一般范数,假设1成立,且 。显然欧式范数下有同样结论。
我们定义由算法生成的σ-场如下:
, 对任意 ,
且 。根据σ-场,在假设1下,我们得到随机次梯度镜面下降法生成的序列 有如下基本性质:
引理1:若假设1成立,则根据算法(7),对任意 , ,有
.
证明:由点 处的一阶必要性条件得:
,对任意
其中 表示Bregman距离函数关于第二个变量的偏导数。由式(6),我们有,
, 对任意
等价地,
. (11)
根据式(5),令 ,则对任意 ,我们有
.
将其带入(11)式,可以发现,对任意 ,
.
由 的强凸性质,以及式(5)可推出,
. (12)
下面求内积项,根据Fenchel’s不等式 ,可得:
, (13)
为范数 的共轭范数。消去 ,我们有
.
在 上取条件期望,再根据假设1,我们得到
.
从而推论得证。
引理2:设F为
上的强凸函数,强凸系数
,若假设1成立,且Bregman距离函数
满足式(10),步长取值满足条件(8),则随机次梯度镜面下降迭代生成的序列
与问题(1)的最优解 满足如下关系:
满足如下关系:
.
证明:在假设1下,根据引理1,令 ,则对任意 ,有
,
由函数F的强凸性可得
.
结合上述两不等式,并对它们求总期望,进一步得:对任意 ,
,(14)
不等式两边同时乘以 ,由 ,则对任意 ,我们有
.
由于 ,将上面不等式从 求和得
,(15)
由于 ,由(14)式知,当 时, 满足如下关系:
。对任意 (16)
联立(15)和(16)式,我们可得到,对任意
,
将上式两边同时乘以 ,然后运用关系 ,从而推论得证。
定理2:设F为 上的强凸函数,强凸系数 。若假设1成立,且Bregman距离函数 满足式(10),步长取(9)中任何一个,则对随机次梯度镜面下降迭代法生成的序列 ,我们有:
, 对任意 ,
则对加权平均迭代序列 ,我们有:
, 对任意 ,
, 对任意 ,
其中 为问题(1)的最优解。
证明:根据引理2,对任意 ,我们有:
.
有步长序列 满足:对任意 , ,所以
, (17)
由F的强凸性以及加权平均迭代序列 的定义,上式可总结为:
, 对任意 ,
又F在 上的强凸性,我们有 ,则
, 对任意 ,
而且由式(17)我们可得:
, 对任意 ,
则由函数 的强凸性,我们有
, 对任意 .
5. 总结
本文在基本的镜面下降方法的基础上引入随机思想,得到随机次梯度镜面下降方法,并将该方法与加权平均迭代法相结合,进一步探讨了带有加权平均迭代 [11] 的随机次梯度下降镜面下降方法。我们考虑了随机次梯度镜像下降法的最优性条件,通过使用自适应步长求得权值,从而得到该方法的加权平均迭代值。本文的创新点是在迭代平均值的构造中使用自适应步长选择来获得权重,通过使用所提出的权值,我们可以恢复强凸函数和仅凸函数的已知速率。
基金项目
国家自然科学基金(11461013),贵州省公共大数据重点实验开放课题项目(2017BDKFJJ012)。
文章引用
周 倩,罗贤兵,王 鑫. 一种非光滑强凸函数的随机次梯度镜面下降算法
A Stochastic Sub-Gradient Mirror Descent Algorithm for Non-Smooth and Strongly Convex Functions[J]. 理论数学, 2018, 08(03): 221-229. https://doi.org/10.12677/PM.2018.83028
参考文献
- 1. Juditsky, A. and Nemirovski, A.S. (2010) First Order Methods for Nonsmooth Convex Large-Scale Optimization, II: Utilizing Problem’s Structure. MIT Press, Cambridge.
- 2. Ben-Tal, A., Margalit, T. and Nemirovski, A. (2001) The Ordered Subsets Mirror Descent Optimization Method with Applications to Tomography. Society for Industrial and Applied Mathematics, 12, 79-108.
- 3. Rakhlin, A., Shamir, O. and Sridharan, K. (2012) Making Gradient Descent Optimal for Strongly Convex Stochastic Optimization. arXiv:1109.5647 [cs.LG]
- 4. Beck, A. and Teboulle, M. (2003) Mirror Descent and Nonlinear Projected Subgradient Methods for Convex Optimization. Operations Research Letters, 31, 167-175. https://doi.org/10.1016/S0167-6377(02)00231-6
- 5. Duchi, J.C., Shalev-Shwartz, S. and Singer, Y. (2010) Composite Objective Mirror Descent. 23rd Conference on Learning Theory, Haifa, 27-29 June 2010, 14-26.
- 6. Sra, S., Nowozin, S. and Wright, S.J. (2011) Optimization for Machine Learning. MIT Press, Cam-bridge.
- 7. Brègman, L.M. (1967) The Relaxation Method of Finding the Common Point of Convex Sets and Its Ap-plication to the Solution of Problems in Convex Programming. USSR Computational Mathematics & Mathematical Physics, 7, 200-217. https://doi.org/10.1016/0041-5553(67)90040-7
- 8. Tseng, P. (2008) On Accelerated Proximal Gradient Methods for Convex-Concave Optimization. SIAM Journal on Optimization.
- 9. 陶蔚, 潘志松, 陶卿. 使用Nesterov步长策略投影次梯度方法的个体收敛性[J]. 计算机学报. 2018 (1).
- 10. Beck, A. and Te-boulle, M. (2009) A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM Journal on Imaging Sciences, 2, 183-202. https://doi.org/10.1137/080716542
- 11. Luong, D.V.N., Parpas, P. and Rueckert, D. (2016) A Weighted Mirror Descent Algorithm for Non-Smooth Convex Optimization Problem. Journal of Optimi-zation Theory & Applications, 170, 900-915. https://doi.org/10.1007/s10957-016-0963-5