Pure Mathematics
Vol.
09
No.
01
(
2019
), Article ID:
28372
,
10
pages
10.12677/PM.2019.91005
A Population Model Driven by Truncated Stable Process
Yingying Yan, Jinying Tong
Department of Mathematics, Donghua University, Shanghai
Received: Dec. 12th, 2018; accepted: Jan. 1st, 2019; published: Jan. 8th, 2019

ABSTRACT
In this paper, we study the population model driven by truncated α-stable process. First, we limit the jump height of the stable process, and then under some assumptions, we prove that the global positive solution of the population model with negative jump still exists. At the same time, by using Khasminskii lemma and Lyapunov function, we obtain the conditions that the model satisfies the stationary distribution and exponential ergodicity. Besides, when
, this model will go extinct.
Keywords:Truncated α-Stable Process, Population Model, Stationary Distribution, Exponential Ergodicity, Extinction
由截尾稳定过程驱动的种群模型
燕莹莹,童金英
东华大学数学系,上海

收稿日期:2018年12月12日;录用日期:2019年1月1日;发布日期:2019年1月8日

摘 要
本文主要研究了由截尾α-稳定过程驱动的种群模型。在本文中我们首先限制稳定过程的跳跃高度,然后在一些假设下,证明带负跳的种群模型的全局正解仍然存在;同时我们利用Khasminskii引理及Lyapunov函数得到了该模型满足平稳分布和指数遍历的条件。此外,我们还给出了当
时,该模型将趋于灭绝。
关键词 :截尾α-稳定过程,种群模型,平稳分布,指数遍历,灭绝性

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在生态系统中,种群是占有一定空间的一群同种个体的自然组合,一般情况下,在没有人为干扰的系统中,种群的数量可以基本保持稳定,但这种稳定却不是一直不变的。因为它总是受到各种因素的影响。而种群生态学即研究某一生态群体个体数量的变化规律。
二十世纪初,Lotka [1] 和Volterra [2] 在不考虑外界环境影响的条件下提出了用一个常微分方程来研究种群的数量变化,即:
这就是著名的Lotka-Volterra模型。
但随着研究的深入,学者们开始在Lotka-Volterra模型中考虑外界环境对种群数量
的影响。比如Gard [3] 和Liu [4] 等用布朗运动来刻画外界环境产生的噪声,从而提出随机Lotka-Volterra模型:
(1)
其中,
表示标准布朗运动。
然而,在现实生活中,种群的数量经常会因为一些突如其来的因素而在瞬间发生巨大的变化。比如一场自然灾害可以使得种群数量骤减,气温的变化引起种群的迁入和迁出。而研究表明这个变化是服从方差为无穷的幂律分布 [5] [6] [7] 。因此Zhang [8] 等提出由谱正稳定过程驱动的种群模型:
(2)
其中我们称只有正跳的稳定过程叫做谱正稳定过程,其Lévy测度定义为:
他们证明了当随机微分方程的噪声较小时,方程具有唯一稳定分布;而当噪声较大时,方程则以概率1灭绝。
而本文在Zhang [8] 等的基础上研究由稳定过程驱动的带负跳的种群模型,则随机微分方程形式为:
(3)
其中
是α-对称稳定过程,且我们给出以下几个假设(A):
(A1) 给定系数a > 0,b > 0,假定
> 1;
(A2) 假定z满足
。则对应的Lévy测度
(4)
则本文我们要探讨在测度(4)式下,随机模型(3)得到的结论与Zhang [8] 等人论文中的结果有什么不同。即:
1) 在满足假设(A)的情况下,该随机模型(3)是否仍存在唯一正解;
2) 随机噪声要满足什么条件,该随机模型(3)具有唯一平稳分布和指数遍历;
3) 在什么条件下,该随机模型(3)将以概率1灭绝;而当模型永远持续时,又要满足什么条件?
2. 全局正解
在给出方程(3)具有唯一平稳分布和指数遍历的条件前,我们先来说明这个随机微分方程的全局正解性。
引理2.1:在假设(A)成立的条件下,对任意给定的初值
,随机微分方程(3)对所有的
,存在唯一的全局正解
,并且该解以概率1位于
中,即
证明:令
是爆炸时间,在
上,由Zhang [8] 等定理2.1证明可知,方程(3)的解
满足
其中,
显而易见,
,则可推出
。从而对任意
,
,都有
。
下面我们证当
时,
。
令
,且足够大使得
。对任意的整数
,定义停时
设
,显然
是单调递增的且
,令
,有
,因此如果我们能证明
,那么
,且对任意
,
。
定义一个非负函数
其中:
。对
,由Itô公式 [9] [10] 可知
(5)
其中
(6)
是一个局部鞅。
我们令
,其中
由变量代换
得,
令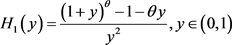 。可知
在区间(0, 1)上有界,则存在一个正数
,使得
,因此有
。可知
在区间(0, 1)上有界,则存在一个正数
,使得
,因此有
(7)
通过泰勒展开
和变量代换
得:
(8)
从而存在一个正数
,使得
,则有
(9)
而另一方面,
定义
。则由洛必达法则可得:
。从而有
(10)
经过变量代换
则
(11)
把(9)式和(11)式代入(6)式,得
则这必存在一个正数C,使得
。
对
,结合(6)式取期望得,
(12)
令
,则对充分大的数k有,
已知
,且
在区间
递减,而在
递增。
于是
那么从(12)式得,

令
,我们得到
,这是一个矛盾。则我们必有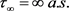 。即
。
。即
。
于是,
成立,证明完成。
3. 平稳分布
引理3.1 [11] :设
是正则有界的(即光滑),若存在
中的一个有界开子集U,使得它的闭包
,且满足:
(i)
;
(ii)
对
的每一个紧子集K (使得
)均成立,其中令
,且
。
则随机微分方程具有唯一平稳分布。
接下来,利用上面的引理来给出本节的主要结论。
定理3.1:在假设(A)成立的条件下,如果
,则随机微分方程(3)具有唯一平稳分布。
证明:设M为一个充分大的正实数,
显然
,满足引理3.1中的条件(i)。接下来,我们将验证引理3.1中的条件(ii)。
首先考虑函数
函数
在区间
上递减,在区间
上递增。则
由Itô公式 [9] [10] 得:
(13)
其中
(14)
对于积分
,由
,我们有
令
,则不难得到
。从而可得:
(15)
又有
(16)
将
代入(14)式,可得
(17)
联合(9)式和(17)式,则有
如果满足定理中的条件
,则存在足够大的数M,使得
而我们又知道
设
,从而
。当
时,我们得到
。
根据引理3.1,定理3.1证明完成。即方程(3)具有唯一的平稳分布。
4. 指数遍历
引理4.1 [12] :
为一个马尔可夫过程。如果存在一个Lyapunov函数V(x)和两个正常数
,K使得
其中L是马尔可夫过程
的无穷小生成元,则我们称
是指数遍历的。
定理4.1:在假设(A)成立的条件下,如果
,则随机微分方程(3)是指数遍历的。
证明:首先找出一个Lyapunov函数:
则通过Itô公式计算得:
(18)
其中
就是(14)式的定义,而
由基本不等式
,再通过变量代换
,得
。
代入(18)式有
从而得到
(19)
若满足条件 ,则必然存在一个正常数
,使得
,则必然存在一个正常数
,使得
于是存在一个正常数K,对
,(19)式有
由引理4.1可知,随机微分方程(3)是指数遍历的。证毕。
5. 灭绝性
在本节中,我们将讨论随机微分方程(3)的灭绝性。在证明之前,我们首先引入定义及鞅的强大数定律。
定义5.1:对任意初值
,如果模型的解
满足
,也就是说
。则我们称模型是灭绝的。
引理5.1:(鞅的强大数定律 [13] )令
是一个局部鞅,定义
若有
,则可推出
。
定理5.1:对任意初值
,在假设(A)成立的条件下,随机微分方程(3)的解
服从
特别地,若满足
,则
。
证明:由Itô公式可得
(20)
其中,
是一个局部鞅。
我们首先讨论积分
。
令
。对
求导可得
已知
,则可得
。
因此我们有
(21)
而对于
,由Meyer尖括号过程可知,
其中,
则由基本不等式
,得
于是通过上式可知,
由鞅的强大数定律得
(22)
再把(21)式和(22)式代入(20)式,我们有
上式两端同除以
并令
,可得
此外,若有
,则定理5.1的最后结论成立。即
以概率1灭绝。
文章引用
燕莹莹,童金英. 由截尾稳定过程驱动的种群模型
A Population Model Driven by Truncated Stable Process[J]. 理论数学, 2019, 09(01): 36-45. https://doi.org/10.12677/PM.2019.91005
参考文献
- 1. Lotka, B.A.J. (1956) Elements of Physical Biology. Williams and Wilkins.
- 2. Volterra, V. (1926) Variazioni e flut-tuazioni del numero d’individui in specie animali conviventi. Memoire della Reale Accademia Nazionale dei Lincei, 33, 31-113.
- 3. Gard, T.C. (1984) Persistence in Stochastic Food Web Models. Bulletin of Mathematical Biology, 46, 357-370.
https://doi.org/10.1007/BF02462011
- 4. Liu, H. and Zhien, M. (1991) The Threshold of Survival for System of Two Species in a Polluted Environment. Journal of Mathematical Biology, 30, 49-61.
https://doi.org/10.1007/BF00168006
- 5. Richardson, L. (1948) Variation of the Frequency of Fatal Quarrels with Magnitude. Publications of the American Statistical Association, 43, 523-546.
https://doi.org/10.1080/01621459.1948.10483278
- 6. Schaefer, J.A. and Mahoney, S.P. (2003) Spatial and Temporal Scaling of Population Density and Animal Movement: A Power Law Approach. Écoscience, 10, 496-501.
https://doi.org/10.1080/11956860.2003.11682797
- 7. Pinto, C.M.A., Lopes, A.M. and Machado, J.A.T. (2012) A Review of Power Laws in Real Life Phenomena. Communications in Nonlinear Science and Numerical Simulation, 17, 3558-3578.
https://doi.org/10.1016/j.cnsns.2012.01.013
- 8. Zhang, Z., Zhang, X. and Tong, J. (2017) Ex-ponential Ergodicity for Population Dynamics Driven by α-Stable Processes. Statistics and Probability Letters, 125, 149-159.
https://doi.org/10.1016/j.spl.2017.02.010
- 9. Applebaum, D. (2009) Lévy Processes and Stochastic Calculus. 2nd Edition, Cambridge University Press, Cambridge.
https://doi.org/10.1017/CBO9780511809781
- 10. Sato, K. (1999) Lévy Processes and Infinitely Divisible Dis-tributions. Cambridge University Press, Cambridge.
- 11. Khasminskii, R. (1980) Stochastic Stability of Differential Equations. Sijthoff and Noordhoff.
https://doi.org/10.1007/978-94-009-9121-7
- 12. Meyn, S.P., Tweedie, R.L., et al. (1993) Stability of Markovian Processes III: Foster-Lyapunov Criteria for Continuous Time Processes. Advances in Applied Probability, 25, 518-548.
https://doi.org/10.2307/1427522
- 13. Lipster, R. (1980) A Strong Law of Large Numbers for Local Martingales. Stochastics, 3, 217-228.
https://doi.org/10.1080/17442508008833146






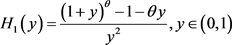 。可知
在区间(0, 1)上有界,则存在一个正数
,使得
,因此有
。可知
在区间(0, 1)上有界,则存在一个正数
,使得
,因此有
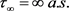 。即
。
。即
。 ,则必然存在一个正常数
,使得
,则必然存在一个正常数
,使得