Pure Mathematics
Vol.
09
No.
02
(
2019
), Article ID:
29224
,
12
pages
10.12677/PM.2019.92020
Advances in Inverse Isoperimetric Inequalities
Yanli Jia1, Xiang Gao2*
School of Mathematical Sciences, Ocean University of China, Qingdao Shandong

Received: Feb. 16th, 2019; accepted: Mar. 6th, 2019; published: Mar. 13th, 2019

ABSTRACT
The most classical geometric inequality in mathematics is the isoperimetric inequality, which describes the relationship between the area and perimeter of the region enclosed by a simple close curve in a Euclidean plane. Starting from the most classical isoperimetric inequalities, this paper explores the development process of reverse isoperimetric inequalities and summarizes the research results of reverse isoperimetric inequalities in recent years. It mainly introduces the development process and main research results of reverse isoperimetric inequalities in plane oval domain, high-dimensional Euclidean surface, popular surface and some special surface from three aspects.
Keywords:Isoperimetric Inequality, Inverse Isoperimetric Inequality, Isoperimetric Deficit, Inverse Bonnesen Type Inequality
逆向等周型不等式的研究进展
贾艳丽1,高翔2*
中国海洋大学数学科学学院,山东 青岛

收稿日期:2019年2月16日;录用日期:2019年3月6日;发布日期:2019年3月13日

摘 要
数学中最经典的几何不等式就是等周不等式,它刻画了欧式平面中的由简单闭曲线所围区域的面积与周长之间的关系。本文从最经典的等周不等式出发,探究逆向等周不等式的发展进程并归纳总结近年来逆向等周不等式的研究成果,主要从三个方面分别介绍了逆向等周不等式在平面卵形域、高维欧式曲面、流行曲面及一些特殊曲面的发展过程及主要研究成果。
关键词 :等周不等式,逆向等周不等式,等周亏格,逆Bonnesen型不等式

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
研究背景
等周问题是几何与凸几何分析中最经典最重要的问题。等周不等式是几何与分析中最重要的不等式之一,它被广泛运用于分析、代数、运筹学等其它数学分支和物理、医学、建筑等其它学科中,获得几何不等式是包含测度理论的重要运用之一,最早和最经典的几何不等式就是等周不等式,它刻画了平面域的几何量(周长、面积)之间的关系。即若 为平面上长为 ,所围面积为 的简单闭凸曲线,有 。等周问题的认识与研究经历了漫长的历史,早在古希腊时代,人们就知道了此结论,但它的严格证明,直到1870年,德国数学家Weierstrass才用变分的方法给出了等周问题解存在性的完整证明。1902年,德国数学家Hurwitz用Fourier级数和Green定理给出了纯解析的证明,1939年德国数学家Schmidt得到了等周不等式的简化证明。随后,数学家又给出了许多精彩的证明并把等周不等式推广到高维欧式空间、常曲率空间、仿射空间、极小曲面以及特殊的黎曼流形中,并研究加强和推广的等周不等式,即Bonnesen型不等式和欧式平面中关于两凸域混合面积的Minkowski不等式和Bonnesen型混合等周不等式。高维曲面上等周不等式与Sobolev不等式等价,具有非常重要的研究价值,而逆向等周不等式作为等周不等式的一种逆形式,在各个领域中同样有非常重的地位。
2. 逆向等周型不等式
近年来数学家们已经对逆向等周不等式做了深入的研究并取得许多著名的结果并运用于各个领域。由于在高维欧式平面上等周不等式与Sobolev不等式等价,故本文主要从三个方面来探究逆向等周不等式的发展过程,主要总结近年来逆向等周不等式在平面卵形域、流行上及一些特殊曲面上的发展过程及主要研究成果。
2.1. 欧式平面R2上的逆向等周不等式的发展过程及主要结果
依据经典的等周不等式,数学家定义了刻画 上的凸域 与半径为 的圆的差别的等周亏格
。
1920年Bonnesen发现了一系列形如
的不等式,其中 为与区域 相关的非负几何量,当且仅当 为圆盘时 ,此类不等式称为Bonnesen型不等式。最著名的Bonnesen型不等式为
设 为平面中由简单闭曲线围成的面积为 ,周长为 的域,则
其中 和 分别表示 的最大内切圆半径和最小外接圆半径。当且仅当 为圆盘时等号成立。
后继数学家用不同的方法给出许多不同形式的Bonnesen型不等式(例如文献 [1] - [7] ),与Bonnesen型不等式相应的是逆Bonnesen型不等式,即
其中 为与 相关的非负几何量。人们对等周亏格的研究有很长的历史,以前的工作主要是对下界的估计,但等周亏格上界的估计即对逆Bonnesen型不等式的研究日益丰富得到了许多非常重要的结果。
1933年,对 中的卵形域 (边界有连续的曲率半径的凸域),Bottema得到一个非常著名的逆Bonnesen型不等式(详见文献 [8] )
其中, 和 分别为 的边界 的曲率半径 的最小值与最大值,当且仅当 即 为圆盘时等号成立。
1955年,Pleijel对Bottema的结果做了进一步推广,得到如下结果(详见文献 [9] )
。
Howard、高翔、潘生亮、张洪等人用分析及曲率流的方法得到一些对于 中卵形区域上成立的逆Bonnesen型不等式(详见文献 [10] [11] [12] [13] )
,(1)
其中 为一常数, 为 的曲率中心的轨迹所围区域 的面积,当且仅当 为圆盘即 为一个点时等号成立。
注:(1)式中的 可能非正。
最近ChangJun Li和Xiang Gao在结果(1)的基础上对平面上卵形区域上成立的逆向等周不等式做了进一步研究,得到了如下结果,并利用傅里叶级数证明了该结果(详见文献 [14] )。
定理1:若 为欧式平面 上严格凸 闭曲线,长度为L,所围区域面积为A,记 为曲率中心的轨迹所围面积,则对任意的常数 满足
,
有
, (2)
, (3)
, (4)
, (5)
, (6)
其中, 为 的曲率, 和 分别表示曲线 和曲率中心的轨迹的曲率半径。当且仅当 为圆周时不等式(3)~(6)等号成立;不等式(2)等号成立的充分必要条件为 为圆周且参数 满足
。
在文献 [9] 和文献 [15] 中,Stantalo得到单位球面 上的卵形区域的逆Bonnesen型不等式
。
其中 和 分别表示具有最大测地曲率半径与最小测地曲率半径的测地圆盘的周长和面积,当且仅当 为测地圆盘时等号成立。
周家足在此基础上,得到对欧式平面 中任意凸区域均成立的逆Bonnesen型不等式(详见文献 [16] [17] )。
定理2:若 为欧式平面 上任一周长为 ,所围面积为 的凸域,则有
,
,
。
其中 和 分别表示 的最大内切圆半径和最小外接圆半径,上述不等式的等号均成立当且仅当 为圆盘时。
张洪,罗永超等在文 [18] 中得到利用Ros不等式得到与下面的不等式(详见文献 [12] ):设 为欧式平面 中长度为 的简单闭曲线, 围成一面积为 的域 ,设 为 的弧长,若 的曲率 处处不为零,则有
等价的逆向等周不等式(详见文献 [18] )。
定理3:设
为欧式平面
中长度为
的简单闭曲线,
围成一面积为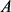 的域
的域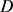 ,设
,设 为
为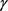 的弧长,若
的弧长,若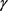 的曲率
的曲率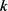 处处不为零,则有
处处不为零,则有
 , (7)
, (7)
当且仅当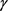 为圆时等号成立。
为圆时等号成立。
戴勇,吴现荣等结合式(7)的结果并利用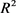 中卵形域的Ros定理及其加强形式,得到如下
中卵形域的Ros定理及其加强形式,得到如下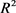 中卵形域中与Ros等周亏格相关的几个逆Bonnesen型不等式(详见文献 [19] )。
中卵形域中与Ros等周亏格相关的几个逆Bonnesen型不等式(详见文献 [19] )。
定理4:设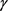 为欧式平面
为欧式平面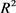 中长度为
中长度为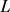 的简单闭曲线,
的简单闭曲线,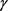 围成一面积为
围成一面积为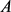 的域
的域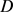 ,设
,设 为
为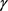 的弧长,若
的弧长,若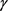 的曲率
的曲率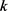 处处不为零,则有
处处不为零,则有
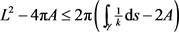 ,
,
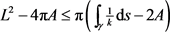 ,
,
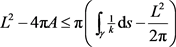 。
。
当且仅当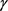 为圆时等号成立。
为圆时等号成立。
若令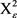 为2维单连通,曲率为常数
为2维单连通,曲率为常数 的曲面,则对
的曲面,则对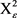 上的
上的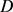 ,令
,令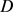 的面积为
的面积为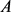 ,
,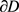 的周长为
的周长为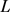 ,可定义关于
,可定义关于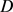 的等周亏格
的等周亏格
 ,
,
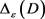 刻画了面积为
刻画了面积为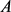 周长为
周长为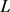 的域与测地圆盘之间的差别。
的域与测地圆盘之间的差别。
Li和Zhou仿照Bottema的不等式的方法,得到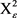 上卵形区域
上卵形区域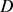 的与Bonnesen型不等式相似的不等式(详见文献 [20] )
的与Bonnesen型不等式相似的不等式(详见文献 [20] )
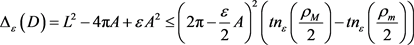 。
。
其中定义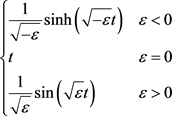 ,
,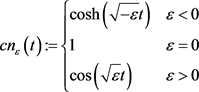 ,则
,则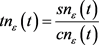 ,
,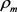 和
和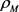 分别为
分别为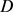 的边界
的边界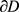 的曲率半径
的曲率半径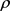 的最小值与最大值,当且仅当
的最小值与最大值,当且仅当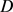 为圆盘时等号成立。
为圆盘时等号成立。
Xia Yunwei、Xu Wenxue等在文 [21] 中仿照Zhou和Ren所提出的命题得到了 上一般凸区域的逆Bonnesen型不等式(详见 [17] [22] )。
上一般凸区域的逆Bonnesen型不等式(详见 [17] [22] )。
定理5:若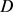 为
为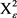 上所围面积为
上所围面积为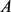 ,周长为
,周长为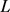 的凸域,则有
的凸域,则有
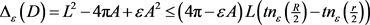 ,
,
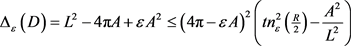 ,
,
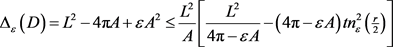 。
。
其中 和
和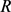 分别表示
分别表示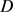 的最大内切圆半径和最小外接圆半径,当且仅当
的最大内切圆半径和最小外接圆半径,当且仅当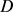 为圆盘时等号成立。
为圆盘时等号成立。
2.2. 特殊曲面上的逆向等周不等式的发展过程及主要结果
2.2.1. 星形域上的逆向等周不等式
Jianbo Fang在文献 [23] 中研究了星形域的逆向等周不等式,将平面上凸曲线的曲率中心的轨迹推广到星形域上,但星形曲线没有曲率中心的轨迹,故利用极坐标在星形区域上建立一种新的参数轨迹,并利用此结果建立了星形平面曲线的逆向等周不等式。
对星形曲线,我们考虑轨迹
 ,
,
其中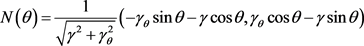 为
为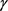 的单位内法向量。则由
的单位内法向量。则由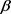 所围闭区域的面积为
所围闭区域的面积为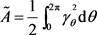 。
。
故若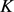 为星形区域,面积为
为星形区域,面积为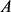 ,周长为
,周长为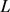 ,则有
,则有
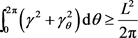 ,
,
当且仅当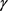 为圆周曲线时等式成立。依据上式可得如下星形平面曲线的逆向等周不等式(详见文献 [23] )。
为圆周曲线时等式成立。依据上式可得如下星形平面曲线的逆向等周不等式(详见文献 [23] )。
定理6:若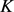 为星形区域,面积为
为星形区域,面积为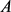 ,周长为
,周长为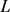 ,
,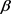 的边界所围面积为
的边界所围面积为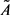 ,则有
,则有
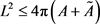 ,
,
当且仅当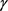 为圆周曲线时等式成立。
为圆周曲线时等式成立。
2.2.2. 2维Alexandrov空间上的逆向等周不等式
在文献 [24] 中,Alexandrov提出流行上同胚于一圆盘A.D的2维曲率有界的区域上的不等式
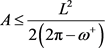 ,
,
其中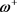 表示区域的正曲率,当且仅当区域与在顶点处的曲率
表示区域的正曲率,当且仅当区域与在顶点处的曲率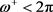 的右圆锥的侧面等距时等号成立。
的右圆锥的侧面等距时等号成立。
Alexander A.在此基础上提出Alexandrov空间上的逆向等周不等式(详见文献 [25] )。
定理7:设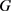 为与曲率大于等于
为与曲率大于等于 的2维Alexandrov空间上的圆盘同胚的区域,若
的2维Alexandrov空间上的圆盘同胚的区域,若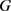 的边界曲线
的边界曲线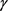 为
为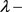 凸,周长为
凸,周长为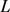 ,所围面积为
,所围面积为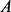 ,则有
,则有
1) 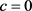
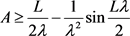 ;
;
2) 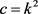
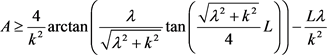 ;
;
3) a)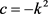 且
且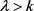
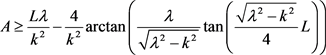 ;
;
b)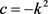 且
且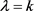
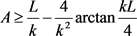 ;
;
c)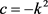 且
且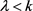
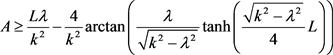 。
。
当且仅当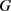 为曲率为常数
为曲率为常数 的平面上的长度为
的平面上的长度为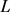 的
的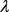 -凸弓形区域。
-凸弓形区域。
2.2.3. Wulff流上的逆向等周不等式
Wulff流起源于方向朝外以单位速度流动的正常流,故对平面上的两有界凸区域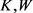 ,其各自边界
,其各自边界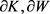 的支持函数分别为
的支持函数分别为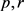 ,
,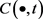 为一族凸闭曲线,则Wulff流可定义为
为一族凸闭曲线,则Wulff流可定义为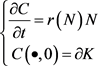 ,其中
,其中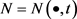 为
为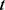 时刻单位法向量。
时刻单位法向量。
令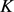 为沿向外法线方向以单位速度增长的平面凸区域,则相应区域的面积可表示为
为沿向外法线方向以单位速度增长的平面凸区域,则相应区域的面积可表示为
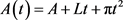 。
。
若设凸区域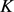 的面积为
的面积为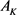 ,周长为
,周长为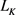 ,函数
,函数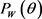 为凸体
为凸体 的支撑函数,且
的支撑函数,且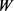 的面积为
的面积为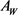 ,周长为
,周长为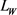 ,则Wulff-Steiner多项式可表示为(参考文献 [26] )
,则Wulff-Steiner多项式可表示为(参考文献 [26] )
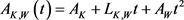 ,
,
其中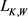 为
为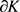 关于
关于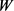 的Wulff长度,可表示为
的Wulff长度,可表示为
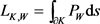 ,
,
其中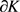 为
为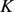 的边界,
的边界, 为
为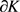 的弧长参数,则
的弧长参数,则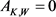 的判别式
的判别式
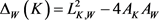 (8)
(8)
为Wulff等周亏格(详见文献 [26] )。且当仅当 为单位圆盘时
为单位圆盘时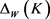 与
与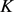 的等周亏格相等。
的等周亏格相等。
故根据Wulff等周亏格式(8),得到如下Wulff流上的逆向等周不等式(详见文献 [26] [27] )。
定理8:设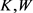 为
为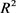 上两卵形体,面积分别为
上两卵形体,面积分别为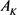 和
和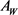 ,记
,记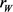 和
和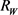 分别为
分别为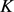 的最大
的最大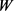 -内接圆半径和最小
-内接圆半径和最小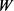 -外切圆半径,则有
-外切圆半径,则有
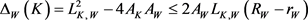 ,
,
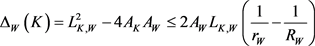 ,
,
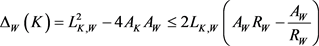 ,
,
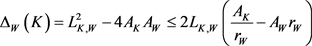 。
。
其中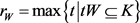 ,
,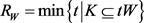 ,当且仅当
,当且仅当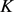 与
与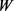 位拟时等式成立(若存在一些
位拟时等式成立(若存在一些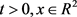 ,使得
,使得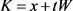 成立,则称
成立,则称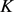 与
与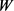 位拟)。
位拟)。
2.3. 欧式平面上任意两个区域上的逆向等周不等式的发展过程及研究结果
数学家们不满足于只在单一的区域上研究等周不等式,依照平面上等周不等式的研究思路,得到了对平面上任意两个简单闭曲线所围成的域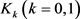 ,记它们周长为
,记它们周长为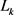 ,所围面积为
,所围面积为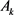 ,则有
,则有
 。
。
此不等式称为对称混合等周不等式,当其中一个域为圆盘时该不等式为经典等周不等式(详见文献 [5] [28] )。
同样可根据对称混合等周不等式得定义,定义关于平面上两域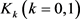 的对称混合等周亏格
的对称混合等周亏格
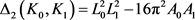
周家足等人的到对平面上任意两凸域均成立的逆Bonnesen型对称混合不等式(详见文献 [5] [29] )。
令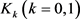 为
为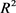 中任两所围面积为
中任两所围面积为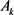 ,周长为
,周长为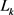 的凸域,则有
的凸域,则有
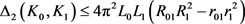 ,
,
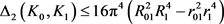 ,
,
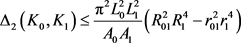 。
。
其中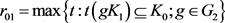 ,
,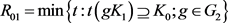 分别为
分别为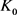 相对于
相对于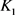 的相对内半径与相对外半径,
的相对内半径与相对外半径,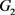 为
为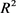 中的刚体运动群。
中的刚体运动群。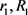 分别为
分别为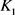 的最大内切圆半径和最小外接圆半径,当且仅当
的最大内切圆半径和最小外接圆半径,当且仅当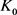 与
与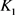 均为圆盘时等号成立。当
均为圆盘时等号成立。当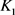 为单位圆盘时,上述逆Bonnesen型对称混合不等式为逆Bonnesen型不等式。
为单位圆盘时,上述逆Bonnesen型对称混合不等式为逆Bonnesen型不等式。
周家足,王鹏富等人利用积分几何中的Poincare运动公式,Blasohke运动公式及包含测度理论研究关于平面两凸域的Bonnesen型对称混合不等式,得到了一些关于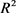 中任意两卵形域的逆Bonnesen型对称混合不等式(详见文献 [29] )。
中任意两卵形域的逆Bonnesen型对称混合不等式(详见文献 [29] )。
设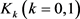 为
为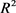 中任两卵形域,若记
中任两卵形域,若记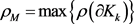 ,
,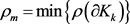 ,令
,令
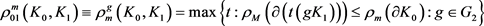 ,
,
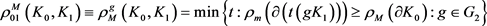 ,
,
则有
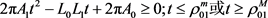 。
。
当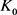 和
和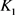 均为圆盘时等号成立。此外通过计算可从上式得
均为圆盘时等号成立。此外通过计算可从上式得
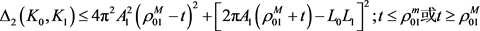 , (9)
, (9)
当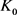 和
和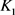 均为圆盘时等号成立。
均为圆盘时等号成立。
令式(9)中关于平面两卵形域的对称混合亏格的上界为关于t的函数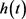 ,即
,即
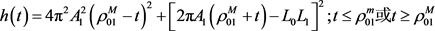 。
。
则知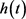 在
在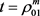 和
和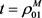 时取得最小值。故当
时取得最小值。故当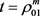 时,有
时,有
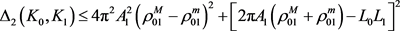 , (10)
, (10)
当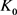 和
和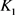 均为圆盘时等号成立。当
均为圆盘时等号成立。当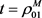 时,有如下定理。
时,有如下定理。
定理9:设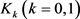 为
为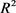 中面积为
中面积为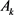 ,周长为
,周长为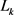 的两卵形域,则有
的两卵形域,则有
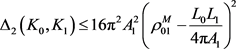 , (11)
, (11)
当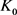 和
和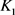 均为圆盘时等号成立。
均为圆盘时等号成立。
同理对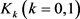 为
为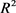 中面积为
中面积为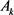 ,周长为
,周长为 的两卵形域,有
的两卵形域,有
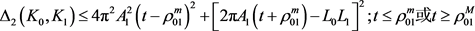 , (12)
, (12)
当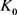 和
和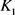 均为圆盘时等号成立。
均为圆盘时等号成立。
令式(12)中关于平面两卵形域的对称混合亏格的的上界为关于t的函数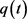 ,即
,即
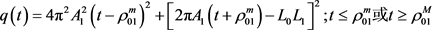 。
。
则知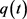 在
在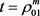 和
和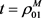 时取得最小值。故当
时取得最小值。故当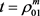 时,即为到式(9)当
时,即为到式(9)当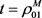 时,有如下定理。
时,有如下定理。
定理10:设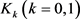 为
为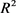 中面积为
中面积为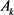 ,周长为
,周长为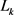 的两卵形域,则有
的两卵形域,则有
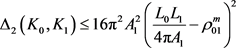 , (13)
, (13)
当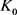 和
和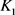 均为圆盘时等号成立。
均为圆盘时等号成立。
从式(11)与式(13)可得
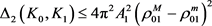 , (14)
, (14)
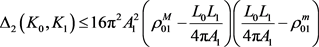 。 (15)
。 (15)
注1):当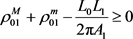 时,式(13)为(10),(11),(12),(14)和(15)中最好的关于平面两卵形域的逆Bonnesen型对称混合不等式;
时,式(13)为(10),(11),(12),(14)和(15)中最好的关于平面两卵形域的逆Bonnesen型对称混合不等式;
当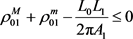 时,式(11)为(10),(11),(13),(14)和(15)中最好的关于平面两卵形域的逆Bonnesen型对称混合不等式。
时,式(11)为(10),(11),(13),(14)和(15)中最好的关于平面两卵形域的逆Bonnesen型对称混合不等式。
2):当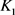 为单位圆盘时,上述关于两卵形域的逆Bonnesen型对称混合不等式变为如下由Bottema,Bokowski,Heil,周家足,潘生亮等人的得到的逆Bonnesen型不等式(详见文献 [1] [8] [10] [17] )。
为单位圆盘时,上述关于两卵形域的逆Bonnesen型对称混合不等式变为如下由Bottema,Bokowski,Heil,周家足,潘生亮等人的得到的逆Bonnesen型不等式(详见文献 [1] [8] [10] [17] )。
 ;
;
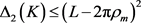 ;
;
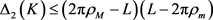 ;
;
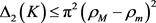 ;
;
 ,
,
当且仅当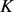 为圆盘时等号成立。
为圆盘时等号成立。
根据欧式空间中混合体积的定义知2维欧式平面中两凸体的混合面积,若设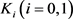 为欧式平面
为欧式平面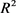 中面积为
中面积为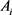 的两凸域,支撑函数为
的两凸域,支撑函数为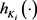 ,弧长微元为
,弧长微元为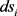 ,则凸域
,则凸域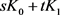 的面积为关于
的面积为关于 和
和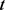 的2次齐次多项式(详见文献文献 [30] )。
的2次齐次多项式(详见文献文献 [30] )。
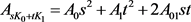 ,
,
其中
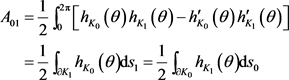
叫做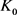 与
与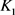 的混合面积。
的混合面积。
罗淼在文献 [30] 中定义欧式平面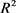 中两凸域的对称混合等拟亏格
中两凸域的对称混合等拟亏格
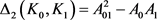 , (16)
, (16)
它刻画了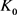 与
与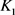 的位拟程度。特别地,当两凸域中有一个微单位圆盘时,对称混合等拟亏格就与另一域的等周亏格等价。
的位拟程度。特别地,当两凸域中有一个微单位圆盘时,对称混合等拟亏格就与另一域的等周亏格等价。
罗淼,周家足等人利用积分几何的平移包含测度,对上式(16)中定义的欧式平面中两凸域的对称混合等拟亏格的上界进行了研究,得到如下的结果。
当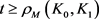 时,有
时,有
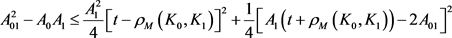 , (17)
, (17)
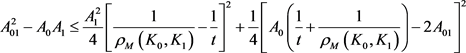 。 (18)
。 (18)
在不等式(17)和(18)中,若令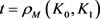 ,分别可得如下逆Bonnesen型对称混合等拟不等式(详见文献 [31] )。
,分别可得如下逆Bonnesen型对称混合等拟不等式(详见文献 [31] )。
定理11:设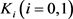 为
为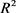 中面积为
中面积为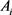 的两凸域,
的两凸域,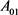 是
是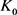 与
与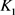 的混合面积,
的混合面积,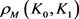 和
和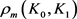 分别为
分别为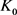 关于
关于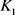 的曲率外半径和曲率内半径,则有
的曲率外半径和曲率内半径,则有
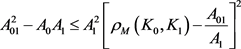 ,
,
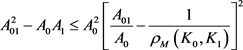 。
。
进一步有(详见文献 [31] )
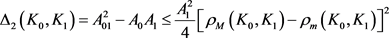 ,
,
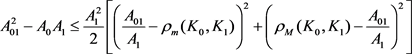 ,
,
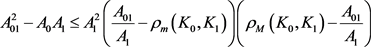 。
。
同理当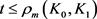 时,有
时,有
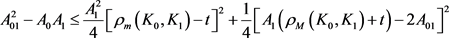 , (18)
, (18)
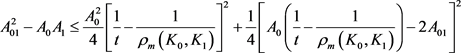 。 (19)
。 (19)
在不等式(18)和(19)中,当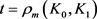 时,可分别得到如下逆Bonnesen型对称混合等拟不等式(详见文献 [30] )。
时,可分别得到如下逆Bonnesen型对称混合等拟不等式(详见文献 [30] )。
定理12:设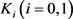 为
为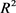 中面积为
中面积为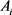 的两凸域,
的两凸域,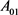 是
是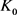 与
与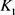 的混合面积,
的混合面积,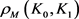 和
和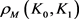 分别为
分别为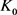 关于
关于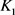 的曲率外半径和曲率内半径,则有
的曲率外半径和曲率内半径,则有
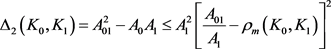 ;
;
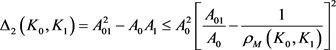 。
。
进一步有
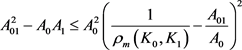 ,
,
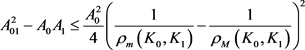 ,
,
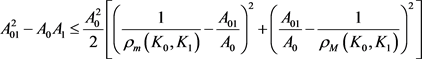 ,
,
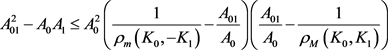 。
。
基金项目
本文由山东省自然科学基金(ZR2018MA006)及山东省研究生导师指导能力提升项目(SDYY17009)支持。
文章引用
贾艳丽,高 翔. 逆向等周型不等式的研究进展
Advances in Inverse Isoperimetric Inequalities[J]. 理论数学, 2019, 09(02): 152-163. https://doi.org/10.12677/PM.2019.92020
参考文献
- 1. Bokowski, J. and Heil, E. (1986) Integral Representation of Quermassintegrals and Bonnesen-Style Inequalities. Archiv der Mathematik, 47, 79-89.
https://doi.org/10.1007/BF01202503 - 2. 周家足. 平面Bonnesen型不等式[J]. 数学学报, 2007, 50(6): 1397-1402.
- 3. Diskant, V. (1973) A Generalization of Bonnesen’s Inequalities. Soviet Mathematics Doklady, 14, 1728-1732.
- 4. Zhang, X.-M. (1997) Bonessen-Style Inequality and Pseudo-Perimeters for Polygons. Journal of Geometry, 60, 188-201.
https://doi.org/10.1007/BF01252226 - 5. 增春娜, 周家足, 岳双珊. 平面两凸域的对称混合等周不等式[J]. 数学学报, 2012, 5(2): 355-362.
- 6. Osserman, R. (1979) The Bonessen-Style Isoperimetric Inequality. The American Mathematical Monthly, 86, 1-29.
https://doi.org/10.1080/00029890.1979.11994723 - 7. Zhou, J. and Cheng, Y. (2012) Some Bonessen-Style Inequality for Higher Dimensions. Acta Mathematica Sinica, 28, 2561-2568.
https://doi.org/10.1007/s10114-012-9657-6 - 8. Bottema, O. (1933) Eineobere Grenze fur das isoperimetrische Defizitebener Kurven. Nederl Akad Wetensch Proc Ser A, 66, 442-446.
- 9. Pleijiel, A. (1955) On konvexa kurvor. Nordisk Math Tidskr, 3, 57-64.
- 10. Pan, S.L. and Zhang, H. (2007) A Reverse Isoperimetric Inequality for Convex Plane Curves. Beitragezur Algebra und Geometrie Contributions to Algebra and Geometry, 48, 303-308.
- 11. Gao, X. (2011) A Note on the Reverse Isoperimetric Inequality. Results in Mathematics, 59, 83-90.
https://doi.org/10.1007/s00025-010-0056-y - 12. Pan, S.L. and Yang, J.N. (2008) On a Non-Local Perimeter-Preserving Curve Evolution Problem for Convex Plane Curves. Manuscripta Mathematica, 127, 469-484.
https://doi.org/10.1007/s00229-008-0211-x - 13. Howard, R. and Treibergs, A. (1995) A Reverse Isoperimetric Inequality, Stability and Extremal Theorems for Plane Curves with Bounded Curvature. Rocky Mountain Journal of Mathematics, 25, 635-684.
https://doi.org/10.1216/rmjm/1181072242 - 14. Li, C.J. and Gao, X. (2015) The Isoperimetric Inequality and Its Stability. Journal of Mathematics, 3, 897-912.
- 15. Santalo, L. (1942) Integral Formulas in Crofton’s Style on the Sphere and Some Inequalities Referring to Spherical Curves. Duke Mathematical, 9, 707-722.
https://doi.org/10.1215/S0012-7094-42-00949-9 - 16. 周家足, 任德麟. 从积分几何的观点看几何不等式[J]. 数学物理学报, 2010(30): 1322-1339.
- 17. Zhou, J.Z., Ma, L. and Xu, W. (2013) On the Isoperimetric Dedicit Upper Limit. Bulletin of the Korean Mathematical Society, 50, 175-184.
https://doi.org/10.4134/BKMS.2013.50.1.175 - 18. 张洪, 罗永超, 徐文学. Bonnesen型Ros等周不等式[J]. 数学的实践与认识, 2015, 45(17): 263-266.
- 19. 戴勇, 吴现荣, 刘朝军. 几个与Ros等周亏格相关的逆Bonnesen型不等式[J]. 数学的实践与认识, 2016, 46(18): 193-196.
- 20. Li, M. and Zhou, J.Z. (2010) An Upper Limit for the Isoperimetric Deficit of Convex Set in Plane of Constant Curvature. SCI China Math, 53, 1941-1946.
https://doi.org/10.1007/s11425-010-4018-3 - 21. Xia, Y. and Xu, W. (2013) Reverse Bonnesen Style Inequalities in a Surface of Constant Curvature. SCI China Math, 6, 1145-4454.
https://doi.org/10.1007/s11425-013-4578-0 - 22. Zhou, J. and Ren, D. (2010) Geometric Inequalities—From Integral Geometry Point of View. Acta Mathematica Scientia, 30, 1322-1339.
- 23. Fang, J. (2017) A Reverse Isoperimetric Inequality for Embedded Starshaped Plane Curves. Archiv der Mathematik, 108, 621-624.
https://doi.org/10.1007/s00013-017-1048-x - 24. Alexandrov, A.D. (1945) One Isoperimetric Inequality Problem. Doklady Akademii Nauk SSSR, 50, 31-34.
- 25. Borisenko, A. (2016) Reverse Isoperimetric Inequality in Two-Dimensional Alexandrov Spaces.
- 26. Green, M. and Osher, S. (1999) Steiner Polynomials, Wulff Flows, and Some New Isoperimetric Inequalities for Convex Plane Curves. Asian Journal of Mathematics, 3, 659-676.
https://doi.org/10.4310/AJM.1999.v3.n3.a5 - 27. Zhang, Z.L. and Zhou, J.Z. (2017) Bonnesen-Style Wulff Is Operimetric Inequality. Journal of Inequalities and Applications, 2017, 42.
https://doi.org/10.1186/s13660-017-1305-3 - 28. 王鹏富, 徐文学, 周家足, 朱促成. 平面两凸域的Bonnesen型对称混合不等式[J]. 中国科学(数学), 2015(45): 245-254.
- 29. 王鹏富. Bonnesen型对称混合不等式[R]. 重庆市: 西南大学, 2016: 45-54.
- 30. 罗淼. Bonnesen型对称混合等拟不等式与 混合质心体[R]. 重庆市: 西南大学, 2016: 56-69.
- 31. Luo, M., Xu, W. and Zhou, J. (2015) Translative Containment Measure and Symmetric Moxed Isohomothetic Inequalities. Science China Mathematics, 58, 2593-3610.
https://doi.org/10.1007/s11425-015-5074-5
NOTES
*通讯作者。