Pure Mathematics
Vol.
10
No.
05
(
2020
), Article ID:
35557
,
15
pages
10.12677/PM.2020.105053
Long Time Behavior of Stochastic Hepatitis C Virus Infection Model with Mixed Switching
Luqiu Huang, Chao Lv, Yuting Pan, Zaitang Huang
School of Mathematics and Statistics, Nanning Normal University, Nanning Guangxi
Received: Apr. 17th, 2020; accepted: May 7th, 2020; published: May 14th, 2020

ABSTRACT
This paper mainly studies the extinction and persistence of a stochastic hepatitis C virus infection model (HCV model) with mixed switching. First, we prove the existence and uniqueness of the solution of the stochastic HCV model. Secondly, we prove the existence and uniqueness of the invariant probability measure of the stochastic HCV model by using the theory of Feller property, invariant control set and Krylov Bogoliubov theorem. Finally, by using the strong ergodicity theorem, Borel-Cantelli lemma and iterated logarithm law, the conditions of extinction and persistence of the stochastic HCV model are obtained.
Keywords:Stochastic HCV Model, Extinction, Permanence, Invariant Probability Measure, Markov Chain

具有混合切换的随机丙型肝炎病毒感染模型的长期性行为
黄露秋,吕超,潘玉婷,黄在堂
南宁师范大学数学与统计学院,广西 南宁

收稿日期:2020年4月17日;录用日期:2020年5月7日;发布日期:2020年5月14日

摘 要
本文主要研究具有混合切换的随机丙型肝炎病毒感染模型(HCV模型)的灭绝性和持久性。首先,证明了随机HCV模型解的存在性唯一性。其次,利用费勒性质、不变控制集和Krylov-Bogoliubov定理等理论,证明了随机HCV模型的不变概率测度的存在唯一性。最后,运用强遍历性定理、波莱尔康特立引理和迭代对数定律等理论,获得了随机HCV模型的灭绝性和持久性的条件。
关键词 :随机HCV模型,灭绝性,持久性,不变概率测度,马尔科夫链

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,全世界持续感染丙型肝炎病毒(HCV),并有罹患慢性肝病,肝硬化和肝细胞癌风险的人口数量逐步增加。由此,丙型肝炎病毒感染已成为一个严重的全球公共卫生问题,备受关注 [1] - [8]。
最早的丙型肝炎病毒感染模型(HCV模型)是由诺伊曼等人提出 [1],具体模型如下
(1.1)
其中
分别为t时刻的未感染肝细胞数量,感染肝细胞量和病毒载量,且
表示细胞总数。S表示未感染的肝细胞可能通过移行或分化成肝细胞前体细胞,以S的构成率增加数量;a表示感染细胞的最大增值速率;b表示未感染细胞的死亡率;
表示使用抗病毒药物治疗所降低的感染率;q表示通过非细胞溶解过程自发治愈感染的肝细胞的治愈率;
表示未感染细胞的最大增值速率;
表示肝细胞游离病毒感染率;
表示感染病毒细胞死亡率;
表示病毒生产率;p表示细胞产生游离病毒的速率;c表示清除游离病毒的速率。
本文考虑以下三个具有混合切换的随机丙型肝炎病毒感染模型的动力学性质。
模型一:与状态无关的马尔科夫状态切换HCV模型
(1.2)
其初始值
,对于实数
,有
。因此,
是一个具有状态空间
的连续时间马尔科夫链,且其具有如下转移概率
(1.3)
其中
,且Q-矩阵
;
。
模型二:仍然是模型(1.2),但此时
是一个具有状态空间
的跳跃过程,对任意
和
,其过渡内核如下所示
(1.4)
无论何时,都有
,其中
。
模型三:考虑到依赖于状态的随机环境和随机扰动的影响,随机HCV模型如下
(1.5)
2. 具有独立于状态的随机HCV模型的灭绝性与持久性
在随机HCV模型(1.2)和(1.3)中,连续时间马尔科夫链
的转移概率与状态无关。令
,,其他变量
的定义与它类似。假设
·
对所有的
, 是局部利普希茨连续的,且存在常数
,使得
;
·
连续时间马尔科夫链
是不可约和正递归的,且其具有不变概率测度
。
下面的引理表明,随机HCV模型(1.2)和(1.3)的唯一解在正象限中,并揭示了肝细胞的总数量有一个上界。
引理2.1 假设
成立,令
。则随机丙型肝炎病毒感染模型(1.2)和(1.3) 有唯一强解
,其解的初始值
。此外,仍有
(2.1)
Proof. 首先由随机模型(1.2)可以得到
(2.2)
又因为
,故有
(2.3)
令
,则有
特别地
对
应用伊藤链式法,有
从而,获得
(2.4)
引理证明完毕。
推论2.2 假设
成立,则随机丙型肝炎病毒感染系统(1.2)的解
具有不变概率测度。
证明:首先注意到
是一个费勒过程。由(2.1)式,可得
(2.5)
对任意
,令
, 是起始点为
的
的过渡内核。对任意
和
,定义概率测度
则对任意的
,由切比雪夫不等式和(2.5)可知,存在充分大的
,使得
因为
是
的紧子集,所以,
是紧的。由Krylov-Bogoliubov’s定理 [9] [10] 可知,
具有不变概率测度。推论证明完毕。
定理2.3 假设
和
成立,并进一步假设存在具有
的
:
和
使得
(2.6)
和
(2.7)
则有
(2.8)
和
(2.9)
证明:设
,由(1.2)和(2.6),可得
(2.10)
从而,获得
(2.11)
因此,利用马氏链的强遍历性定理,除了有
之外,还获得
因此,有
,a.s.
下证
,a.s.,注意到
对
应用伊藤链式法,有
(2.12)
又因为
,a.s.,所以对任意
,存在具有
的
和
,使得
这就意味着
结合(2.12)式可得:只要
就有
(2.13)
由此证得
,a.s.
根据(2.8)有
(2.14)
由(2.2)可以得到下式
结合(2.5)和(2.14)及连续时间马尔科夫链的强遍历性定理,可得(2.7),即
定理2.4令
和
成立,并进一步假设:对任意
, 且有
(2.15)
其中
(2.16)
则
(2.17)
即感染肝细胞具有持久性。
证明:首先声明存在常数
,使得对任意
有
(2.18)
显然,当
时上式成立。所以下面只要证明
时上式也成立就足够了。由
的定义可知
(2.19)
由
的连续性和由(2.19)可知,存在
,使得对任意的
和
有式子(2.18)成立。而对于任意的
,有
(2.20)
因此,当
充分大时,即得(2.18)。
根据(1.2),可得到
(2.21)
从而,得到
(2.22)
然后将(2.10)第一个式子变换后代入上式,并结合(2.5),可获得
(2.23)
于是,有
(2.24)
根据,马尔科夫链
的强遍历性定理,有
由此,可由(2.15)直接推断出(2.17)。
3. 具有依赖于状态的随机HCV模型的灭绝性与持久性
在本节,主要研究在状态相关随机环境的影响下,感染肝细胞的灭绝性与持久性,此处主要研究HCV模型(1.3)和(1.5)。正如我们所知的,(1.3)和(1.5)是一种依赖于状态的机制切换扩散。在过去,有学者对其稳定性,遍历性进行研究 [11] [12] [13] [14],此处不再进行详述。需要注意到,尽管
与
都不是马尔科夫过程,但
确是马尔科夫过程。
假设
(M1) 对于所有的
,矩阵
是不可约和保守的。
(M2)
,其中
。
与HCV模型(eq1.3)和(1.4)相比较,研究模型(1.3)和(1.5)存在更大的挑战,由于此模型下的
不再是一个马尔科夫过程,而是一个跳跃过程,此时经典的连续时间马尔科夫链的遍历定理将不再适用,为了克服这个困难,我们将对
进行随机比较。
根据文献 [12] [13] [14] 可以得到引理如下
引理3.1 假设(M1)和(M2)成立,对每个满足
的
,有
。对每个
,令
假设
和
是不可约的并且满足
(3.1)
则在
中存在两个分别具有转移概率矩阵
和
的连续时间马尔科夫链
,,使得对所有的非减函数
,有
定理3.2 若定理2的假设保持不变且引理3.1成立。并进一步假设
(a) 若
为非减的,且有
(3.2)
则有
(3.3)
和
(3.4)
(b) 若
为非增的,且有
(3.5)
则有
和
(3.6)
证明:一旦得到
,就可以类似地采用定理2.3中的技巧来证明
所以,我们首先要证明
。注意到(2.11)式在这里仍然适用。于是利用
的非减性质和(3.2),并使用
引理3.1及连续时间马尔科夫链的遍历定理即得(3.3)。
若
是非增的,则对应的
是非减的,根据引理3.1得到
于是得到
因此,由(3.5)和连续时间马尔科夫链的遍历定理即得(3.3)。
根据(2.2)式,获得
从而,结合(2.5)和(3.3)以及引理3.1和连续时间马尔科夫链的遍历定理,即可推出(3.4)和(3.6)。
定理3.3 假设定理2.3和引理3.1的假设条件成立,并进一步假设
为非减的,且有
(3.7)
其中
的含义如(2.16)所示;或者
为非增的,且有
(3.8)
则有
(3.9)
证明:我们注意到,在目前的框架下(2.24)式仍然成立。于是应用引理3.1和连续时间马尔科夫链的强遍历定理及
的非降(或非增)性质和(3.7)或(3.8))式,即得(3.9)。
4. 具有混合切换的随机HCV模型的灭绝性与持久性
在本节,我们将随机HCV模型(1.2)和(1.3)或(1.4)进一步拓展为模型(1.5)。在这个部分,我们仍令
。在完成主要结果证明之前,我们先准备以下两个引理。
引理4.1 对任意
,存在常数
,使得
(4.1)
证明:根据系统(1.5),可知
(4.2)
从而,有
(4.3)
其中
;
。
接下来,令
,根据伊藤公式,可获得
(4.4)
运用杨氏不等式:
,得到
(4.5)
其中常数
,相应地。根据格朗沃尔不等式可知,对于常数
,有
(4.6)
此外,通过BDG不等式和杨氏不等式,结合(4.4),则存在常数
,使得对任意
,
(4.7)
从而,结合(4.6)式,即得(4.1)式。
引理4.2 下列不等式成立
(4.8)
证明:为了证明(4.8)成立,我们只需要证明
(4.9)
和
(4.10)
在这里,我们将p限制在
之间,通过BDG不等式和(4.1)式可知,存在常数
,使得
(4.11)
对任意常数
和每个实数
,令
由切比雪夫不等式及(4.11)式,可得
又因为级数
收敛,于是利用波莱尔—康特立引理,可以得到
由C的任意性可知(4.9)式成立。
下证(4.10)式成立 令
显然,
,另一方面,(4.11)式意味着
(4.12)
因此,由( [15], Theorem 5)知,(4.10)式成立。
类似地,可以得到以下结果
(4.13)
定理4.1 假设
和
及引理3.1中的条件成立,并进一步假设存在具有
的
和
,使得
。
(a) 若
为非减的,且有
(4.14)
则有
(4.15)
和
(4.16)
(b) 若
为非增的,且有
(4.17)
则有
和
(4.18)
证明:为了使证明更加简化,记
由伊藤公式及
,可得
(4.19)
由引理4.2知
(4.20)
令
为
的二次变差,则有
由此,根据连续鞅的强大数定理,可得
(4.21)
结合(4.20)和(4.21)及
非降(或非增)的性质,并利用引理3.1和连续时间马尔科夫链的强遍历性定理,即得
这意味着对任意
充分小,存在
和
,使得
(4.22)
令
,且对任意
,
由(4.21)得
这就意味着必定会存在
和
,使得
(4.23)
而后,利用随机积分的迭代对数定律 [16] [17],可以得到
因此,必定存在
和
,使得
(4.24)
由常数变易公式,由(4.23)和(4.24)式可知,对任意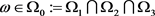 和
,
和
,
(4.25)
显然,经观察可知,必定会存在实数
和
,使得
(4.26)
将(4.26)式代入(4.25)式,并由
的任意性,可得(4.15)式成立。
结合(4.15),根据(4.2)和(4.13)式可得
(4.27)
结合引理3.1即得(4.16)和(4.18)式。
基金项目
国家自然科学基金(41665006、11561009),广西自然科学基金(2018GXNSFAA380240)。
文章引用
黄露秋,吕 超,潘玉婷,黄在堂. 具有混合切换的随机丙型肝炎病毒感染模型的长期性行为
Long Time Behavior of Stochastic Hepatitis C Virus Infection Model with Mixed Switching[J]. 理论数学, 2020, 10(05): 433-447. https://doi.org/10.12677/PM.2020.105053
参考文献
- 1. Neumann, A., Lam, N., Dahari, H., et al. (1998) Hepatitis C Viral Dynamics in Vivo and the Antiviral Efficacy of In-terferon-Alpha Therapy. Science, 282, 103-107. https://doi.org/10.1126/science.282.5386.103
- 2. Bostan, N. and Mahmood, T. (2010) An Overview about Hepatitis C: A Devastating Virus. Critical Reviews in Microbiology, 6, 91-133. https://doi.org/10.3109/10408410903357455
- 3. Akhtar, S. and Carpenter, T. (2013) Stochastic Modelling of Intra-Household Transmission of Hepatitis C Virus: Evidence for Substantial Non-Sexual Infection. Journal of Infection, 2, 179-183. https://doi.org/10.1016/j.jinf.2012.10.020
- 4. Qesmi, R., Wu, J., Wu, J. and Heffernan, J. (2010) Influence of Backward Bifurcation in a Model of Hepatitis B and C Viruses. Mathematical Biosciences, 224, 118-125. https://doi.org/10.1016/j.mbs.2010.01.002
- 5. Jopling, C., Yi, M., Lancaster, A., Lemon, S. and Sarnow, P. (2005) Modulation of Hepatitis C Virus RNA Abundance by a Liver-Specific Micro-RNA. Science, 309, 1577-1581. https://doi.org/10.1126/science.1113329
- 6. Shi, R. and Cui, Y. (2016) Global Analysis of a Mathematical Model for Hepatitis C Virus Transmissions. Virus Research, 217, 8-17. https://doi.org/10.1016/j.virusres.2016.02.006
- 7. Bao, J. and Shao, J. (2018) Asymptotic Behavior of SIRS Models in State-Dependent Random Environments.
- 8. Blé, G., Esteva, L. and Peregrino, A. (2018) Global Analysis of a Mathematical Model for Hepatitis C Considering the Host Immune System. Journal of Mathematical Analysis and Applications, 461, 1378-1390. https://doi.org/10.1016/j.jmaa.2018.01.050
- 9. Anderson, W. (1991) Continuous-Time Markov Chains. Springer, Berlin. https://doi.org/10.1007/978-1-4612-3038-0
- 10. Bellet, L. (2006) Ergodic Properties of Markov Process. In: Open Quantum Systems II, Springer, Berlin, 1-39. https://doi.org/10.1007/3-540-33966-3_1
- 11. Khasminskii, R., Zhu, C. and Yin, G. (2007) Stability of Re-gime-Switching Diffusions. Stochastic Processes and Their Applications, 117, 1037-1051. https://doi.org/10.1016/j.spa.2006.12.001
- 12. Mao, X. and Yuan, C. (2006) Stochastic Differential Equations with Markovian Switching. Imperial College Press, London. https://doi.org/10.1142/p473
- 13. Chen, X., Chen, Z., Tran, K. and Yin, G. (2019) Recurrence and Ergodicity for a Class of Regime-Switching Jump Diffusions. Applied Mathematics & Optimization, 80, 415-444. https://doi.org/10.1007/s00245-017-9470-9
- 14. Yin, G. and Zhu, C. (2010) Hybrid Switching Diffusions Properties and Applications. Springer, Berlin. https://doi.org/10.1007/978-1-4419-1105-6
- 15. Chow, Y. (1965) Local Convergence of Martingales and the Law of Large Numbers. The Annals of Mathematical Statistics, 36, 552-558. https://doi.org/10.1214/aoms/1177700166
- 16. Da Prato, G. and Zabczyk, J. (1996) Ergodicity for Infinite Di-mensional Systems. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511662829
- 17. Ikeda, N. and Watanabe, S. (1989) Stochastic Differential Equations and Diffusion Processes. North Holland, Amsterdam.







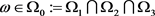 和
,
和
,