Pure Mathematics
Vol.
10
No.
11
(
2020
), Article ID:
38586
,
9
pages
10.12677/PM.2020.1011123
Weierstrass函数的盒维数与Riemann-Liouville分数阶积分的阶之间联系更进一步的研究
高鸿博,梁永顺
南京理工大学理学院,江苏 南京

收稿日期:2020年10月16日;录用日期:2020年11月6日;发布日期:2020年11月13日

摘要
本文中,我们更完整地对IE上Weierstrass函数分形维数与Riemann-Liouville分数阶微积分的阶之间进行了研究。即当α + v不再小于1时,Weierstrass函数的Riemann-Liouville分数阶积分的分形维数被证明是1。
关键词
分形维数,Riemann-Liouville分数阶积分,Weierstrass函数,Lipschitz函数,Hölder条件
Further Discussion on Relationship between Fractal Dimension of Weierstrass Function and Order of Riemann-Liouville Fractional Integral
Hongbo Gao, Yongshun Liang
Institute of Science, Nanjing University of Science and Technology, Nanjing Jiangsu

Received: Oct. 16th, 2020; accepted: Nov. 6th, 2020; published: Nov. 13th, 2020

ABSTRACT
In this paper, we investigate further relationship between fractal dimension of the Weierstrass function on IE and the order of fractional calculus in Riemann-Liouville. That is, when α + v is no longer less than 1, the fractal dimension of the Riemann-Liouville fractional integral of Weierstrass function is proved to be 1.
Keywords:Fractal Dimension, Riemann-Liouville Fractional integral, Weierstrass Function, Lipschitz Function, Hölder Condition

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
[1] [2] 中,作者证明了至多可数个无界变差点的连续函数其分形维数为1。同时,在 [3] 中,作者构造了一个[0, 1]上的无界变差函数,该函数经Riemann-Liouville分数阶积分后被证明分形维数是1。很自然地,我们会想去研究分形维数与含有不可数个无界变差点的连续函数间的关系。而这个问题到目前尚未得到明确的答案。Weierstrass函数是含有不可数个无界变差点的连续函数中的一个典型例子。本文将对其盒维数进行研究。
[4] 中,作者讨论了Weierstrass函数的盒维数与Riemann-Liouville分数阶积分的阶的关系。为方便起见,本文中将用IE表示闭区间[0, 1]。我们可以通过换元,将IE替代为任意闭区间[a, b],其中a严格小于b。Weierstrass函数定义将在下面给出。
例1.1 [5] [6]
令 ,,Weierstrass函数可记为
(1.1)
而,
其中Weierstrass函数在IE上图像的盒维数 [5] 记为 。图1为Weierstrass函数取定参数后的图像。

Figure 1. W(x)
图1. W(x)
定义1.2 [7] [8]
f(x)为定义在IE上的连续函数,v > 0,定义 ,当 时,f(x)的v阶Riemann-Liouville积分定义如下
(1.2)
u > 0,定义 ,当 时,f(x)的u阶Riemann-Liouville微分定义如下
(1.3)
定理1.3 [4]
g(x)表示Weierstrass函数W(x)的Riemann-Liouville分数阶积分, 且 ,则存在足够大的λ使得下式成立
而m(x)表示函数W(x)的Riemann-Liouville分数阶微分,其中 ,则存在足够大的λ使得下式成立
作者在 [4] 中对上述结果做的讨论中,Riemann-Liouville分数阶积分的阶v需要满足特定条件,即 且 。作者并没有给出当 或者 时的结果。因此,我们很自然地会考虑 时,
是否依然成立。当 时,结果又将如何?
本文主要研究当 时,Weierstrass函数W(x)的Riemann-Liouville分数阶积分的盒维数。
2. 定义及符号
为了便于讨论,我们在此给出盒维数的定义。
定义2.1 [5] [6]
令 为 上的有界子集,Nδ(F)是直径最大为δ可以覆盖F的集的最少个数,则F的下盒维数定义如下
(2.1)
对应地,F的上盒维数定义如下
(2.2)
如果这两个值相等,则称这共同的值为F的计盒维数或盒维数,记为
(2.3)
由上述定义方式可知,一个闭区间上连续函数的盒维数未必存在,但是由(2.1)和(2.2)可知,其上盒维数和下盒维数是确定存在的。
令
表示f(x)在IE上的图像。如此一来
就可以分别表示f(x)在IE上图像的上盒维数、下盒维数以及盒维数。用C表示与x取值无关的正常数,为了方便计算,即使在同一行,C也可能表示两个不相等的常数。
由定义2.1以及 [9],我们可以得到如下基本性质,可以用来估计一个闭区间上连续函数的上盒维数、下盒维数以及盒维数。
性质2.2
令f(x)为一个连续函数,其定义域为闭区间[0, 1],记作 。对于任意f(x),
若f(x)在IE上盒维数存在,则可得
由性质2.2可知,任意一个闭区间IE上的连续函数,总有上盒维数的自然上界2以及下盒维数的自然下界1。
3. 主要结论
在 [5] 中,通过例11.3,作者证明了Weierstrass函数在IE上满足α-阶Hölder条件。接下来,我们将给出满足α-阶Hölder条件的连续函数经阶为v的Riemann-Liouville分数阶积分后函数的盒维数( )。
f(x)为IE上的连续函数,且 ,若下面的不等式成立
则称f(x)在IE上满足α-阶Hölder条件。若存在一个正数δ0使得
对于任意 以及任意满足 的y成立,则称f(x)在IE上满足局部α-阶Hölder条件。相比于IE上的α-阶Hölder条件,连续函数在IE上的局部α-阶Hölder条件更容易满足。
定理3.1
假设f(x)为在IE上定义良好的连续函数,且存在 ,使得函数f(x)满足α-阶Hölder条件。 的定义如第一部分所述,令 ,则我们可以考虑 的结果。若 ,则 为IE上有界的连续函数且
(3.1)
证明 令 且 ,由(1.2)得
令 且定义
因为
在IE上可微,故
令 且 ,故
因为 在IE上可微,由微分中值定理可得,存在某个确定的 使得
注意到
因为f(x)满足α-阶Hölder条件,故
因此
即
所以
取 则
(3.2)
由(3.2)可知, 为IE上一个满足Lipschitz条件的连续函数。任意满足Lipschitz条件的连续函数一定是有界变差函数。由 [10] 或 [11] 中的结论可得,有界变差连续函数的盒维数一定是1。故(3.1)得证。
由定理1.3以及定理3.1,我们可以得到如下结果。
注3.2
令f(x)为定义在IE上的连续函数,且存在 ,使其满足局部α-阶Hölder条件。同时,当 且 ,令 定义为(1.2)所述。若 ,同理可得, 为IE上的有界变差函数。因此可以得到如下结果
定理3.3
令W(x)为一个Weierstrass函数, 表示W(x)的v阶Riemann-Liouville分数阶积分。再令 ,若 ,对于足够大的λ,下式成立
(3.3)
若 ,对于足够大的λ,下式成立
(3.4)
证明 (3.3)可由定理 1.3直接得到。由 [5] 中例11.3以及定理3.1可得(3.4)。
4. 图像
在这一部分,我们会给出几个图例,这些例子也说明了我们在上一部分得到的结果。
例4.1
令 ,,我们可以得到
为了方便讨论,上述函数记为G0(x)。令G1(x)、G2(x)以及G3(x)分别表示G0(x)的1/3、1/2和2/3阶Riemann-Liouville 分数阶积分。由定理3.3可知:
为了更进一步地说明,下面我们将给出图例,图2~5分别表示G0(x)、G1(x)、G2(x)以及G3(x)。
与图2相比,我们可以发现图4中的G2(x)的图像曲线更光滑。在图5中,曲线已没有尖点存在,因为G3(x)是可微的,也就是说G3(x)是一个有界变差函数。
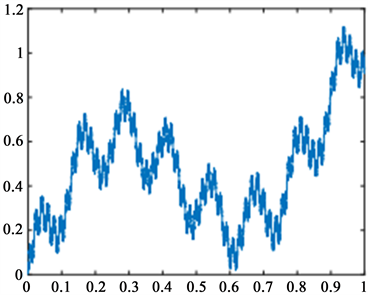
Figure 2. G0(x)
图2. G0(x)

Figure 3. G1(x)
图3. G1(x)

Figure 4. G2(x)
图4. G2(x)
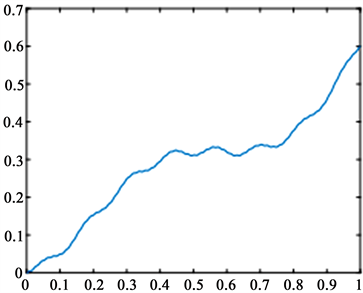
Figure 5. G3(x)
图5. G3(x)
5. 结论
在 [4] 中,作者在 的条件下给出了如下结论
.
本文中,我们更完整地对IE上Weierstrass函数分形维数与Riemann-Liouville分数阶微积分的阶间的关系进行了研究,即当α + v不再小于1时,Weierstrass函数的Riemann-Liouville分数阶积分被证明是Lipschitz 函数,故下式成立
事实上,关于Weierstrass函数Riemann-Liouville分数阶积分性质的问题还值得进一步研究,例如当Riemann-Liouville分数阶积分的阶满足 时,Weierstrass函数是否可微。
基金项目
感谢国家自然科学基金(批准号12071218)、江苏省自然科学基金(批准号12071218)资助的课题以及中央高校基础研究经费(批准号30917011340)的支持。
文章引用
高鸿博,梁永顺. Weierstrass函数的盒维数与Riemann-Liouville分数阶积分的阶之间联系更进一步的研究
Further Discussion on Relationship between Fractal Dimension of Weierstrass Function and Order of Riemann-Liouville Fractional Integral[J]. 理论数学, 2020, 10(11): 1035-1043. https://doi.org/10.12677/PM.2020.1011123
参考文献
- 1. Wang, J. and Yao, K. (2017) Dimension Analysis of Continuous Functions with Unbounded Variation. Fractals, 25, 1730001. https://doi.org/10.1142/S0218348X1730001X
- 2. Liang, Y.S. and Su, W.Y. (2017) Fractal Dimension of Certain Continuous Functions of Unbounded Variation. Fractals, 25, 1750009. https://doi.org/10.1142/S0218348X17500098
- 3. Li, Y. and Xiao, W. (2017) Fractal Dimension of Rie-mann-Liouville Fractional Integral of Certain Unbounded Variational Continuous Function. Fractals, 25, 1750047. https://doi.org/10.1142/S0218348X17500475
- 4. Yao, K., Su, W.Y. and Zhou, S.P. (2005) On the Connection between the Order of the Fractional Calculus and the Dimension of a Fractal Function. Chaos, Solitons and Fractals, 23, 621-629. https://doi.org/10.1016/j.chaos.2004.05.037
- 5. Falconer, K.J. (1990) Fractal Geometry: Mathematical Foundations and Applications, John Wiley Sons Inc., New York. https://doi.org/10.2307/2532125
- 6. 文志英. 分形几何的数学基础[M]. 上海: 科技教育出版社, 2000.
- 7. Oldham, K.B. and Spanier, J. (1974) The Fractional Calculus. Academic Press, New York.
- 8. Miller, K.S. and Ross, B. (1993) An Introduction to the Fractional Calculus and Fractional Differential Equations. John Wiley Sons Inc., New York.
- 9. Liang, Y.S. (2018) Fractal Dimension of Riemann-Liouville Fractional Integral of 1-Dimensional Continuous Functions. Fractional Calculus and Applied Analysis, 21, 1651-1658. https://doi.org/10.1515/fca-2018-0087
- 10. Liang, Y.S. (2010) Box Dimensions of Riemann-Liouville Fractional Integrals of Continuous Functions of Bounded Variation. Nonlinear Analysis, 72, 4304-4306. https://doi.org/10.1016/j.na.2010.02.007
- 11. Verma, S. and Viswanathan, P. (2018) A Note on Katugampola Fractional Calculus and fractal Dimensions. Applied Mathematics and Computation, 339, 220-230. https://doi.org/10.1016/j.amc.2018.07.035