Applied Physics
Vol.07 No.05(2017), Article ID:20726,10
pages
10.12677/APP.2017.75021
Band Diagram Calculations of Dispersive Photonic Crystals Based on COMSOL Weak Form Equation
Yunfei Xu, Zhihong Hang
Collaborative Innovation Center of Suzhou Nano Science and Technology, College of Physics Optoelectronics and Energy, Soochow University, Suzhou Jiangsu

Received: May 6th, 2017; accepted: May 24th, 2017; published: May 27th, 2017

ABSTRACT
In order to study dispersive photonic crystals (PCs), we introduce a numerical finite element method based on weak form equation in COMSOL, which transforms the complex band diagram problem into a simple eigenvalue problem by solving the eigenvalue with respective to wave vector k by frequency. The advantages of the method are illustrated by two examples. The equi-fre- quency contours close to the Dirac-like cone dispersion of a square-lattice PC can be calculated with much less time than traditional methods. We also succeeded in obtained the edge states on the bearded edge and the zigzag edge of a honeycomb PC with a dispersive negative background medium which is numerical unstable for traditional methods.
Keywords:Numerical Methods, Weak Form, Photonic Crystals, Band Diagram
基于COMSOL弱形式方程求解 色散光子晶体能带
徐云飞,杭志宏
苏州大学物理与光电·能源学部,苏州纳米科技协同创新中心,江苏 苏州
收稿日期:2017年5月6日;录用日期:2017年5月24日;发布日期:2017年5月27日

摘 要
为了研究光子晶体复杂色散关系,基于有限元数值仿真软件COMSOL Multiphysics, 我们发展了一套基于COMSOL弱形式方程光子晶体能带的计算方法。通过频率求解波矢k的本征值,将传统方法很难求解的色散能带问题转化为简单线性的本征值问题。利用这一新的数值工具,我们首先对比分析了无色散简单正方晶格光子晶体的体能带结构,弱形式方法与现有方法得到完全一致的能带结果,验证了这种计算方法的正确性。利用这种求解方法能快速求解光子晶体的等频率曲线(equi-frequency contour), 我们也验证了我们研究的正方晶格光子晶体具有类狄拉克锥能带结构。我们将这种方法应用于具有色散负介电常数背景下类石墨烯蜂巢晶格光子晶体的能带结构计算,这是传统光子晶体能带计算方法难以求解的结构。我们发现,在这种光子晶体的胡须状(Bearded)和锯齿状(Zigzag)界面都存在光子界面态。
关键词 :数值求解,弱形式,光子晶体,能带结构

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着半导体的发展人们有了控制电子传输的手段,半导体技术带来的技术革命对人类文明有着深远的影响。在半导体和能带理论的发展下,科学家们开始探索周期性介质中的电磁波传播问题,希望能够找到类比半导体调控电子来调控光子的材料和结构。
1987年由Yablonovitch [1] 和John [2] 分别独立提出光子晶体的概念,将不同折射率的材料在空间做周期性排列,构成光子晶体。其具有和半导体类似的导带、禁带等光子晶体能带结构使得人们可以对光的传播进行任意调控。光子晶体的初期主要工作就是寻找光子禁带结构,将光局域正在很小局域能够大大提高光子的使用效率,具有很高的应用价值。光子晶体的发展是伴随着凝聚态理论发展的。拓扑绝缘体的研究刚刚获得了2016年的诺贝尔物理学奖。随着具有狄拉克色散关系光子晶体能带的发现 [3] ,如何构建拓扑绝缘体的光学类比,研究光子晶体能带的体拓扑性质,构建具有拓扑性质的光子界面态/边缘态是光子晶体研究的最新发展。
光子晶体能带的计算最早也类比了电子晶体能带结构的计算方法,如平面波展开法 [4] 、传输矩阵法 [5] 和时域有限差分法 [6] 等。在求解材料介电常量与频率无关的光子晶体能带结构问题时,其是一个求解线性本征值问题。如平面波展开法求解时,通常给定布洛赫波矢k,扫描整个最简布里渊区边界求解出相应的本征频率f从而求解出能带。但是当研究的光子晶体材料具有色散介电常数,即ε = ε(f)为频率f相关时,便成为一个非线性本征值求解问题,求解变得非常困难。时域有限差分法求解含时域的麦克斯韦方程时,采用一次性脉冲分析(宽频),结合非线性谐波分析。但是其网格分割只有正方形,在求解非规边和色散能带时会变得异常复杂。为了更为方便的研究色散光子晶体能带结构问题,我们基于数值求解软件COMSOL Multiphysics中的弱形式方程,重新构建了光子晶体本征方程,给定频率f,来求解布洛赫波矢k的本征值。这样原本复杂的具有色散材料非线性求解问题被重新转化为简单的线性本征值求解问题。
本文简单介绍了如何在COMSOL Multiphysics中设置弱形式方程来求解光子晶体能带,和具体的参数设置,文中所有计算都是基于COMSOLMutiphysics 4.3版本。并通过两个例子,求解了具有狄拉克点色散的光子晶体能带,验证了拓扑关联的光子界面态的存在,证明我们发展的新方法在将来拓扑绝缘体的光学类比,拓扑光子学的研究中会起到很大的作用。
2. 偏微分方程的弱形式介绍
用数学方法描述真实的物理问题时,一般有三种描述方式。1、偏微分方程形式(Partial Differential Equation, PDE);2、能量最小化形式;3、弱形式(Weak Form)。他们都是同一物理方程的不同等效形式,针对特定条件有各自的优势。其中我们最常见的便是偏微分方程。PDE方程一般都有对应的解析解,当难以得到其解析解时,便需要根据变分原理或能量最小化原理转化为积分形式的泛函数变分问题求解。积分形式适合用有限元元求解,而弱形式可以看做对积分变量连续性要求更低,形式更一般的能量最小化形式了。COMSOL Mutiphysics [7] [8] 是求解多物理场的一款有限元数值求解软件,通过内建多种物理方程及相应求解器,可以对互相耦合的复杂物理问题进行数值求解,是物理学研究中非常重要的工具。COMSOL Multiphysics本身是一款有限元的求解器,可以设定将所需求解的PDE方程转化为弱形式,再进行求解。但不是所有问题都能通过内置弱形式模块解决,这时了解弱形式方程及其有限元算法对求解实际物理问题很有帮助。
在求解光子晶体能带时,当使用COMSOL内置的本征值求解模块时,需要预先定义好其最简布里渊区边界,COMSOL会自动随布洛赫波矢 的变化求解得到其相应频率
的变化求解得到其相应频率 的本征值。在求解色散材料问题时,即介电常数
的本征值。在求解色散材料问题时,即介电常数 或者磁导率
或者磁导率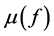 是频率相关函数,由于
是频率相关函数,由于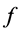 未知,COMSOL内置本征值求解模块将无法求解,这个时候就需要借助自定义弱形式方程来求解了。
未知,COMSOL内置本征值求解模块将无法求解,这个时候就需要借助自定义弱形式方程来求解了。
考虑介质中传播电磁波的麦克斯韦方程可以以磁场H或者电场E形式来表达。以电场形表达式其波动方程为:
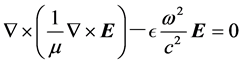 (1)
(1)
 是计算区域的介电常数/磁导率。由于介质做周期性排列,其介电常数和磁导率也是周期性的。根据布洛赫定理,电场可以表达为周期性函数和自然指数乘积的形式,
是计算区域的介电常数/磁导率。由于介质做周期性排列,其介电常数和磁导率也是周期性的。根据布洛赫定理,电场可以表达为周期性函数和自然指数乘积的形式,
 (2)
(2)
其中 是电磁波的频率,
是电磁波的频率, 是布洛赫波矢,
是布洛赫波矢,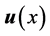 是周期性矢量函数,将方程(2)带入方程(1)我们可以得到
是周期性矢量函数,将方程(2)带入方程(1)我们可以得到 的等价方程:
的等价方程:
 (3)
(3)
在此PDE方程两边乘上任意函数 ,对两边在感兴趣的区域
,对两边在感兴趣的区域 内做积分转化为积分方程形式。与有确定解u不同,有大量不同的函数
内做积分转化为积分方程形式。与有确定解u不同,有大量不同的函数 解满足积分方程的形式,所以函数
解满足积分方程的形式,所以函数 在这里又被称为试函数。试函数在弱形式的有限元求解方法里起了关键作用。有限元方法是基于在满足方程和边界条件的情况下,对感兴趣的区域
在这里又被称为试函数。试函数在弱形式的有限元求解方法里起了关键作用。有限元方法是基于在满足方程和边界条件的情况下,对感兴趣的区域 弱形式进行积分并将积分设为0从而进行求解 [8] 。
弱形式进行积分并将积分设为0从而进行求解 [8] 。
 (4)
(4)
 为积分边界的法向矢量,在外边界,方程(4)的约束,对闭合区间
为积分边界的法向矢量,在外边界,方程(4)的约束,对闭合区间 内积分使得
内积分使得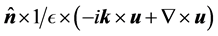 为0.从方程(4)可以知道,
为0.从方程(4)可以知道, ,这是完美电导体边界条件。这是默认边界条件,若无其他外加边界条件则都设置为完美电导体边界。在内部边界,电磁场要满足连续边界条件,
,这是完美电导体边界条件。这是默认边界条件,若无其他外加边界条件则都设置为完美电导体边界。在内部边界,电磁场要满足连续边界条件, ,
, 是内部边界的两侧。
是内部边界的两侧。 的周期性则在原胞外边界用周期性边界条件约束。
的周期性则在原胞外边界用周期性边界条件约束。
而在二维电磁波方程中我们可以做进一步简化, ,作用在
,作用在 和
和 上形成二维向量,
上形成二维向量, 为试函数,所要求解为本征值问题,令
为试函数,所要求解为本征值问题,令 ,而
,而 ,为我们即将求解的二维布洛赫波矢,则方程(4)可以简写为 [9] :
,为我们即将求解的二维布洛赫波矢,则方程(4)可以简写为 [9] :
 (5)
(5)
而在将弱形式输入COMSOL时,只需将方程(5)方括号中的值输入即可。模拟区域是一个原胞,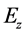 边界条件用周期性边界条件,同样将将布洛赫波矢
边界条件用周期性边界条件,同样将将布洛赫波矢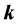 写为
写为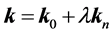 。
。
二维弱形式能带计算设置
COMSOL中未知函数(因变量)u及试函数v的函数表达如下:未知函数u,表达为u, 写为(
写为(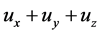 ),在二维电磁波方程弱形式求解中,未知函数为Ez,
),在二维电磁波方程弱形式求解中,未知函数为Ez,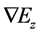 为(
为( );类似的试函数v及
);类似的试函数v及 分量写为,
分量写为, 及
及 ,将弱形式方程输入COMSOL求解域的若干项中,便会自动进行求解运算,其每一个子域可以有不同定义,COMSOL将自动整合不同子域方程。
,将弱形式方程输入COMSOL求解域的若干项中,便会自动进行求解运算,其每一个子域可以有不同定义,COMSOL将自动整合不同子域方程。
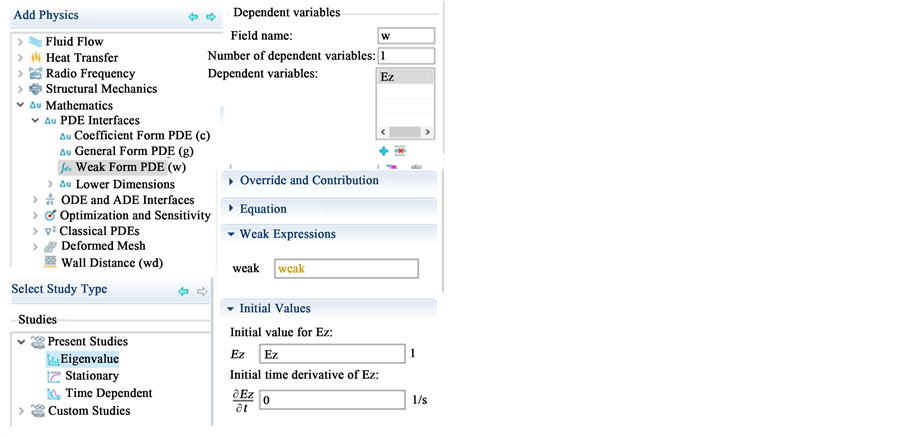
实际计算时,我们在COMSOL物理场中选择弱形式求解模块如图1(a)所示,求解类型选择本征值求解,因变量定义为Ez,绘制完相应光子晶体原胞结构(以图1(b)示意图为例)后,其子域弱项都设置为weak
即弱形式方程,在全局表达式中定义 ,即为二维TM形式电磁波方程的弱形式表达。其中参数设置如表1所示:
,即为二维TM形式电磁波方程的弱形式表达。其中参数设置如表1所示:
 (a) (b)
(a) (b)
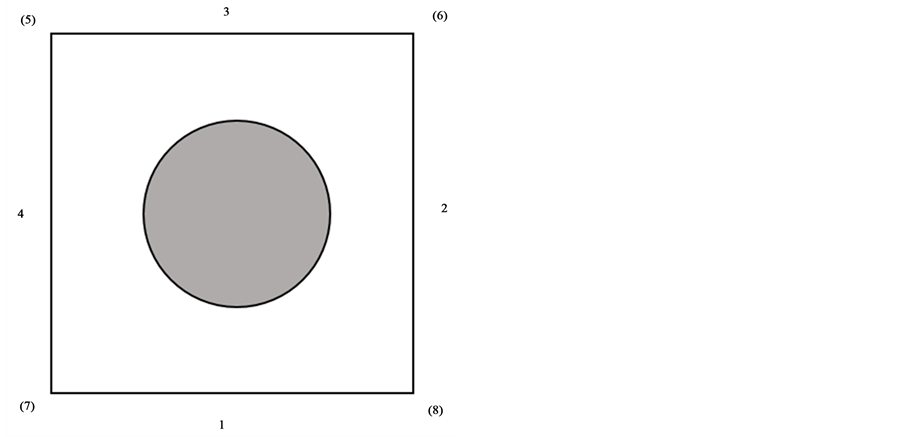
Figure 1. (a) Parameter setting of weak form module in COMSOL; (b) Periodic boundary condition setting
图1. (a) COMSOL中弱形式模块参数设置;(b) 原胞周期性边界条件设置示意图
Table 1. Parameter setting
表1. 参数设置
kx, ky是布洛赫波矢k的x,y分量, epsilon,mu分别为介电常数和磁导率,不同子域中单独设定,所有子域中初始值 设置为Ez。原胞的周期性边界条件的设置非常重要,其需要满足奎特周期性边界,即目标端和源项场值上相差一个相位因子,相位因子的值由边界和波矢的相对距离确定。以图1(b)中二维正方晶格为例,以Ez为约束条件分别设置两对周期性边界,即1,3为一对,2,4为一对分别将1和2边界Ez的值映射到3和4,同时源项和目标项的顶点也需要一一对应,如1,3这对周期边条中,1的源项顶点5,8要分别映射到3边界的顶点6,7。
设置为Ez。原胞的周期性边界条件的设置非常重要,其需要满足奎特周期性边界,即目标端和源项场值上相差一个相位因子,相位因子的值由边界和波矢的相对距离确定。以图1(b)中二维正方晶格为例,以Ez为约束条件分别设置两对周期性边界,即1,3为一对,2,4为一对分别将1和2边界Ez的值映射到3和4,同时源项和目标项的顶点也需要一一对应,如1,3这对周期边条中,1的源项顶点5,8要分别映射到3边界的顶点6,7。
求解本征值时,我们给定因变量为频率。在感兴趣的频率范围内,求解本征波矢k,并将k的值限制在最简布里渊区内。在求解时遇到虚部较大不为0或者接近于0的伪解的出现时,可以借助MATLAB后处理进行后处理将每个频率下的伪解去除,从而可以将整个最简布里渊区内的能带结构求解出来。
3. 利用弱形式方程数值求解复杂光子晶体能带
利用上一部分介绍的COMSOL弱形式方法,我们可以开展对复杂光子晶体的能带计算。弱形式方程是一般有限元计算的通常手法,并非仅仅适用于COMSOL Multiphysics。相信如果可以将这一方法整合并优化,独立于COMSOL单独运行,会对电磁波相关问题具有很大的价值。
我们首先研究了简单无色散正方晶格光子晶体。我们所研究的光子晶体系统参考了Huang等的论文 [10] 。通过调控光子晶体柱的占空比,通过实现偶然简并,在此光子晶体的布里渊中心( 点)具有类狄拉克锥能带结构。而且在狄拉克点频率,此光子晶体可以等效为介电常数和磁导率同时为零的材料,具有很大的应用价值。图2(a)是我们重复引文 [10] ,利用COMSOL内置改变波矢
点)具有类狄拉克锥能带结构。而且在狄拉克点频率,此光子晶体可以等效为介电常数和磁导率同时为零的材料,具有很大的应用价值。图2(a)是我们重复引文 [10] ,利用COMSOL内置改变波矢 求解本征频率模块计算的光子晶体能带结构。具体原胞结构见图(2)插入图。相对介电常数
求解本征频率模块计算的光子晶体能带结构。具体原胞结构见图(2)插入图。相对介电常数 ,相对磁导率
,相对磁导率 ,其光子晶体半径
,其光子晶体半径 ,a为光子晶体晶格常数。图2(b)中插入了正方晶格第一布里渊区的示意图,其高对称点坐标为
,a为光子晶体晶格常数。图2(b)中插入了正方晶格第一布里渊区的示意图,其高对称点坐标为 。在Transverse Magnetic (TM)模式即电场沿z方向下,用上述的弱形式方程方法可以通过改变频率
。在Transverse Magnetic (TM)模式即电场沿z方向下,用上述的弱形式方程方法可以通过改变频率 来求解对应的本征波矢
来求解对应的本征波矢 ,结果见图2(b)。图2(b)和图2(a)完全一致,证明了此种弱形式求解方法的正确性。图2(b)中能带曲线存在间断点,是由于求解方法导致的。为了快速求解我们把波矢的本征值设置在一个较低的数量,而当能带纵向比较平缓时,频率对应纵向本征值
,结果见图2(b)。图2(b)和图2(a)完全一致,证明了此种弱形式求解方法的正确性。图2(b)中能带曲线存在间断点,是由于求解方法导致的。为了快速求解我们把波矢的本征值设置在一个较低的数量,而当能带纵向比较平缓时,频率对应纵向本征值 分布的数量会大大减小,这个时候我们需要在这个平缓能带范围内减小频率步长便能求解到相对较为连贯的能带,但是会大大增加计算时间。
分布的数量会大大减小,这个时候我们需要在这个平缓能带范围内减小频率步长便能求解到相对较为连贯的能带,但是会大大增加计算时间。
3.1. 等频率曲线计算中的应用
光在光子晶体中的传播和光子晶体的等频率曲线息息相关 [11] 。通过设计光子晶体结构来实现各种形状的等频率曲线,从而控制光的传播路径,实现了包括电磁波定向发射 [12] ,超透明 [13] 等各种新奇的

 (a) (b)
(a) (b)
Figure 2. (a) The band structure of square lattice calculated by traditional methods; (b) The band structure calculated by Weak Form
图2. (a) 传统方法计算出的正方晶格光子晶体的能带图;(b) 弱形式方法计算出的同样结构光子晶体能带图
功能。传统上,对等频率曲线的求解需要扫描整个布里渊区范围内所有 下频率f的本征值,再整理所求解数据将感兴趣的频率范围内的值提取出来才能将整个频率范围的等频率曲线画出,计算量相当繁复。而使用弱形式求解我们可以针对特定工作频率f快速求解出最简布里渊区范围内所有波矢k的本征值,从而得到在此频率下的等频率曲线。利用弱形式方程的方法,我们可以很容易优化所需的等频率曲线并实现各种应用。利用我们发展的方法,我们求解了图2正方晶格光子晶体在
下频率f的本征值,再整理所求解数据将感兴趣的频率范围内的值提取出来才能将整个频率范围的等频率曲线画出,计算量相当繁复。而使用弱形式求解我们可以针对特定工作频率f快速求解出最简布里渊区范围内所有波矢k的本征值,从而得到在此频率下的等频率曲线。利用弱形式方程的方法,我们可以很容易优化所需的等频率曲线并实现各种应用。利用我们发展的方法,我们求解了图2正方晶格光子晶体在 点附近的等频率曲线。其计算结果如图3所示。
点附近的等频率曲线。其计算结果如图3所示。
图3中不同的颜色代表不同的频率值f下的计算结果,随着频率的变化等频率曲线在 相交于一点,且在这个频率附近等频率曲线都呈现为圆形。这样的能带具有狄拉克锥能带结构类似的形状,也和引文 [8] 的预言一样。
相交于一点,且在这个频率附近等频率曲线都呈现为圆形。这样的能带具有狄拉克锥能带结构类似的形状,也和引文 [8] 的预言一样。 也与图2中我们计算的正方晶格光子晶体体能带结构
也与图2中我们计算的正方晶格光子晶体体能带结构 点处的狄拉克点频率值完全一致,再一次验证了我们这种算法的正确性。为了方便显示,和平带相关的波矢并没有画出.这样计算每个频率下等频率曲线时间用i5-6300HQ配置电脑用时1.426 s,相比对全布里渊区所有波矢k求解减少90%以上的时间。
点处的狄拉克点频率值完全一致,再一次验证了我们这种算法的正确性。为了方便显示,和平带相关的波矢并没有画出.这样计算每个频率下等频率曲线时间用i5-6300HQ配置电脑用时1.426 s,相比对全布里渊区所有波矢k求解减少90%以上的时间。
3.2. 色散负背景材料能带计算中的应用
我们进一步将这种弱形式求解方法用于研究具有色散负背景材料的光子晶体能带计算。Haldane等已经用二维蜂巢晶格光子晶体实现了与石墨烯能带结构相似具有狄拉克色散关系的二维光子晶体拓扑能带 [3] 。后来Plotnik等人 [14] 利用蜂巢晶格波导阵列,排列组成“光子石墨烯”,在光子石墨烯的Zigzag和Bearded界面上观测到了电子最近邻紧束缚模型预言的在石墨烯相同界面上应该存在的界面态。除此之外,还在Bearded界面首次观测到了另一种新的界面态,并用考虑了次近邻耦合的紧束缚模型进行解释。课题组邵越同学研究了类似的蜂巢晶格光子晶体柱结构,但在Bearded界面上并没有看到类似的现象 [15] 。虽然我们也研究了石墨烯结构的光学类比,但实际物理体系和引文 [14] 有相当的不同。在波导阵列结构,波导之间耦合是通过倏逝波来完成的。这和原子紧束缚近似模型相当类似。而在光子晶体中,光子晶体柱的耦合是靠光/电磁波在背景材料(通常是空气)的传播完成的。耦合的不同,即传播波和倏逝波的不同特性,决定了未能在传统蜂巢光子晶体结构观测到类似的界面态 [16] 。

Figure 3. Equi-frequency diagrams of close to Dirac cone dispersion
图3. 狄拉克锥等频率曲线
如何能够让光子晶体柱之间的耦合也是利用倏逝波的形式来完成呢?如果能够让光子晶体的背景材料的介电常数为负数,那也许就可能利用这样的体系,观测到类比电子紧束缚模型的实验现象。
根据Pendry等人的理论 [17] ,将细金属柱做周期性阵列时,如果柱半径和占空比都远远小于波长,这样的结构可以等效为超材料,其有效介电常数为
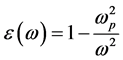 (6)
(6)
ωp为有效等离子频率,可以通过计算金属柱阵列的S参数得出。也就是说,如果在光子晶体柱的空气背景中,插入大量细金属柱,就可以在ω < ωp的频率范围内,用负的有效介电常数材料取代原本的空气背景。根据引文 [17] 的理论,我们设计使用了晶格常数为4.9205mm,半径为0.00375 mm的金属柱阵列,其等效的等离子频率为17.03 GHz (结构见图4(a))。通过调控金属柱占空比,我们可以轻松的改变等效等离子频率,即调控背景材料的有效介电常数,即光子晶体柱之间的倏矢波耦合系数,从而调控光子晶体能带。
但是,引入大量细小的金属柱阵列会使得模型计算十分复杂。由于每一个金属柱十分细小,网格划分密度很高导致计算量非常大。为了降低计算难度,我们需要将背景替换为如公式(6)的具有色散介电常数,并计算光子晶体能带。因为不同频率下介电常数可变,这是传统光子晶体能带计算方法非常难以完成。利用我们发展的弱形式方程,我们可以计算有效负背景光子晶体能带,并与具有金属柱阵列实际结构下的计算结果相对比,如图4所示。其中光子晶体柱选用的材料具有介电常数e= 8.5,磁导率μ = 1,排列成蜂巢晶格,原胞结构如图4(a)所示,选用的晶格常数a = 17.045 mm,介质柱半径r = 3.75 mm。
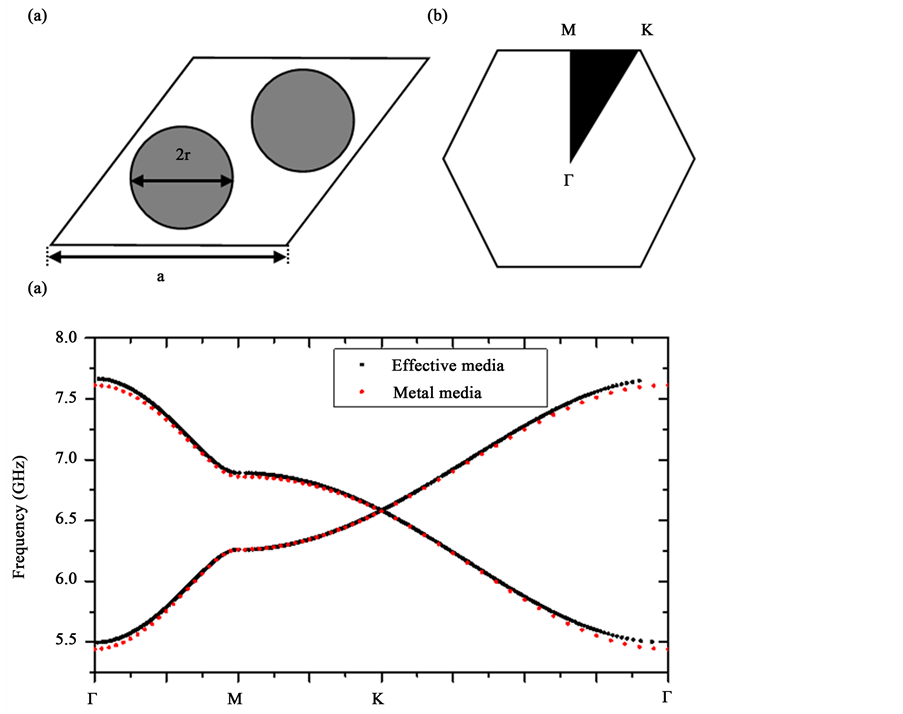
Figure 4. (a) The unit cell of a honeycomb lattice PC; (b) The first Brillouin zone of the system; (c) Comparison of the calculated bulk photonic band diagram of the metal wire background and the effective medium background
图4. (a) 蜂巢晶格光子晶体的原胞结构;(b) 六角晶格光子晶体第一布里渊区示意图;(c) 金属细线背景结构计算与有效介质色散能带计算结果对比
最简布里渊区如图4(b)所示,其高对称点分别为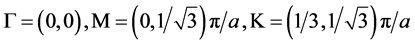 。对比结果如下,图4(c)中红色点为背景材料为前面述蜂巢晶格金属柱阵列的计算结果,而黑色为使用弱形式计算等效色散背景材料下的计算结果,两者基本一致。
。对比结果如下,图4(c)中红色点为背景材料为前面述蜂巢晶格金属柱阵列的计算结果,而黑色为使用弱形式计算等效色散背景材料下的计算结果,两者基本一致。
从我们的能带计算结果可以看到,在 ,在此蜂巢晶格光子晶体存在狄拉克点。在此频率,背景的有效介电常数
,在此蜂巢晶格光子晶体存在狄拉克点。在此频率,背景的有效介电常数 为负数。
为负数。
上面的结果证明了弱形式用于计算色散材料的可行性,我们可以继续利用弱形式方程研究据色散背景的光子晶体,计算研究其光子界面态的存在。
我们研究的体系如图5所示。10个周期的蜂巢光子晶体沿y方向排列。在x方向是周期边界,y方向边界为吸收边界。背景摆放了细金属线结构。光子晶体结构和金属线结构的参数和图4相同。在y方向一边为Bearded边界,一边为Zigzag边界。在考虑了具负色散有效介电常数的情况下,我们在体光子晶体能带之外(图5(a)中黑色点),还得到了局域在边界位置的界面态。图5(a)红色为基于弱形式有效色散介电常数得到的界面态能带,蓝色点为将背景设为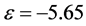 常数时计算得到的界面态。由于界面态色散较平,此时介电常数变化不大,负常数计算界面态也能够定性证明界面态的存在。在波矢范围
常数时计算得到的界面态。由于界面态色散较平,此时介电常数变化不大,负常数计算界面态也能够定性证明界面态的存在。在波矢范围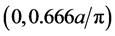 范围,界面态局域在Bearded界面上,如图5(b)所示为
范围,界面态局域在Bearded界面上,如图5(b)所示为 时Bearded界面态的本征
时Bearded界面态的本征

 (a) (b)
(a) (b)
Figure 5. (a) The calculated band diagrams with edge states; (b) The corresponding eigen field distribution of edge mode with bearded edge.
图5. (a) 色散有效介电常数背景下蜂巢结构的投影能带;(b) 10个周期蜂巢光子晶体构成的原胞示意图及bearded界面态的本征场图
场图。这是空气背景光子晶体无法得到的 [15] 。在波矢范围 是局域在Zigzag界面的界面态。
是局域在Zigzag界面的界面态。
我们研究的金属细线背景,在实验上和课题组现有微波实验平台兼容,完全可以开展进一步的实验研究对此类确定性界面态加以实验观测。
4. 结论
本文基于COMSOL Multiphysics中的弱形式求解模块,设计了一种由频率f求解本征波矢k的弱形式求解光子晶体能带结构的算法,并通过计算具有狄拉克色散正方晶格光子晶体的等频率曲线以及负介电常数背景材料光子石墨烯结构中存在的界面态对我们的方法加以验证。不同于传统光子晶体能带求解方法,由波矢k求解频率f,这种求解方式有多种优势,第一,可以快速针对指定频率范围求解出等频率曲线。常用方法只能对整个布里渊区扫描,再通过后处理将特定频率提取出来,其计算量非常大,而且无法计算材料含色散的等频率曲线。第二:这种方法能够计算色散光子晶体的体能带结构,由于输入量是f,这样在这个频率下色散材料的介电常数和磁导率是一个已知量,将常用方法中计算色散介质材料时非线性本征值求解问题转化为线性本征值求解问题;第三,由于是基于COMSOL的弱形式模块求解,我们只需写出相应麦克斯韦方程的弱形式,并将弱形式方程写入COMSOL便能自动进行有限元求解计算,对编程要求非常低,且很容易扩展到类似的系统如声子晶体色散能带求解问题。这种方法为研究更复杂光子晶体模型打造光学类比平台,提供了一种更为便捷的数值仿真手段。进一步的,考虑色散负背景光子晶体体系和电子体系的相似性,利用紧束缚方法来描述,我们可以找到光子晶体中参数与紧束缚模型参数间的一一对应关系,借助于弱形式方程求解方法,将电子体系中的大量研究在光子晶体负背景材料平台上开展类比。
基金项目
国家自然科学基金NSFC11574226。
文章引用
徐云飞,杭志宏. 基于COMSOL弱形式方程求解色散光子晶体能带
Band Diagram Calculations of Dispersive Photonic Crystals Based on COMSOL Weak Form Equation[J]. 应用物理, 2017, 07(05): 149-158. http://dx.doi.org/10.12677/APP.2017.75021
参考文献 (References)
- 1. Yablonovitch, E. (1987) Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Physical Review Letters, 58, 2059-2062. https://doi.org/10.1103/PhysRevLett.58.2059
- 2. John, S. (1987) Strong Localization of Photons in Certain Disordered Dielectric Superlattices. Physical Review Letters, 58, 2486-2489. https://doi.org/10.1103/PhysRevLett.58.2486
- 3. Haldane, F.D. and Raghu, S. (2008) Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Physical Review Letters, 100, Article ID: 013904. https://doi.org/10.1103/physrevlett.100.013904
- 4. Botten, L.C. (2003) Semianalytic Treatment for Propagation in Finite Photonic Crystal Waveguides. Optics Letters, 28, 854-856. https://doi.org/10.1364/OL.28.000854
- 5. Li, Z.Y. and Lin, L.L. (2003) Photonic Band Structures Solved by a Plane-Wave-Based Transfer-Matrix Method. Phycical Review E, 67, Article ID: 046607. https://doi.org/10.1103/physreve.67.046607
- 6. Shi, S.Y., Chen, C.H. and Prather, D.W. (2005) Revised Plane Wave Method for Dispersive Material and Its Application to Band Structure Calculations of Photonic Crystal Slabs. Applied Physics Letters, 86, Article ID: 043104.
- 7. COMSOL Mutiphysics 4.3. https://cn.comsol.com/
- 8. Fietz, C., Urzhumov, Y. and Shvets, G. (2001) Complex K Band Diagrams of 3D Metamaterial/Photonic Crystals. Optics Express, 19, Article ID: 19027.
- 9. Enkrich, C., Wegener, M., Linden, S., et al. (2005) Magnetic Metamaterials at Telecommunication and Visible Fre-quencies. Physical Review Letters, 95, Article ID: 203901. https://doi.org/10.1103/PhysRevLett.95.203901
- 10. Huang, X., Lai, Y., Hang, Z.H., et al. (2011) Dirac Cones Induced by Accidental Degeneracy in Photonic Crystals and Zero-Refractive-Index Materials. Nature Materials, 10, 582-586. https://doi.org/10.1038/nmat3030
- 11. Joannopoulos, J.D., Johnson, S.G., Winn, J.N., et al. (2008) Photonic Crystals: Molding the Flow of Light.
- 12. Bulu, I., Caglayan, H. and Ozbay, E. (2003) Highly Directive Radiation from Sources Embedded inside Photonic Crystals. Applied Physics Letters, 83, 3263-3265.
- 13. Luo, J., Yang, Y., Yao, Z., et al. (2016) Ultratransparent Media and Transformation Optics with Shifted Spatial Dispersions. Physical Review Letters, 117, Article ID: 223901. https://doi.org/10.1103/PhysRevLett.117.223901
- 14. Plotnik, Y., Rechtsman, M.C., Song, D., et al. (2014) Observation of Unconventional Edge States in Photonic Graphene. Nature Materials, 13, 57-62.
- 15. 邵越. “光子石墨烯”的表面态[D]: [学士学位论文]. 苏州: 苏州大学, 2016.
- 16. Wang, J., Shao, Y. and Hang, Z.H. (2016) Observation of the Edge Modes in Photonic Graphene. Progress in Electromagnetic Research Symposium (PIERS), Shanghai, 8-11 August 2016, 812-816.
- 17. Pendry, J.B. (1996) Extremely Low Frequency Plasmons in Metallic Mesostructures. Physical Review Letters, 76, 4773-4776.
