Applied Physics
Vol.08 No.06(2018), Article ID:25473,7
pages
10.12677/APP.2018.86037
Simulation and Life Evaluation of Thermal Stress of Ball Valve in High Temperature Medium Pressure Steam System
Zhulin Dong1, Jianjun Liu2, Shengjian Yu3
1Equipment Procurement Center of Chinese Navy Equipment Department, Beijing
2China Ship Development and Design Center, Wuhan Hubei
3Dalian Shipbuilding Industry Co. Ltd., Dalian Liaoning

Received: Jun. 3rd, 2018; accepted: Jun. 20th, 2018; published: Jun. 27th, 2018

ABSTRACT
Based on the calculation results of the steady-state temperature field, a transient temperature calculation is performed, and then the thermal stress of the entire valve system is calculated based on the results of the transient temperature field. For the valve body local concentrated stress up to 278 MPa, the thermal stress of other components are less than the allowable stress of the material. The fatigue resistance of the valve shell was analyzed.
Keywords:Ball Valve, High Temperature, Heat Stress, Life Assessment
高温中压蒸汽系统球阀热应力仿真计算及 寿命评估
董珠琳1,刘建军2,于胜剑3
1海军装备部装备采购中心,北京
2中国舰船研究设计中心,湖北 武汉
3大连船舶重工集团有限公司,辽宁 大连

收稿日期:2018年6月3日;录用日期:2018年6月20日;发布日期:2018年6月27日

摘 要
基于稳态温度场的计算结果,进行瞬态温度计算,然后基于瞬态温度场结果计算整个阀门系统的热应力。阀体局部集中应力最大达到278 MPa,其他零部件的热应力均小于材料的许用应力。并对阀门承压壳体进行了疲劳敏感性分析。
关键词 :球阀,高温,热应力,寿命评估

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
阀门是管路内流体的控制设备,其基本功能是连通或切断管路内的介质,改变介质的流动状态及流动方向,达到调节介质压力和流量的目的,保护管路及其他设备的正常运行。球阀具有流动阻力小、密封好、可靠性高、启闭速度快等突出特点,不仅在一般工业管路上得到了广泛的使用,而且在核电、航天的液氧与液氢输送管路等行业中亦被普遍采用 [1] 。国内目前研制的球阀大部分在常温介质中使用 [2] [3] ,对于高温过热蒸汽介质中使用的球阀研究较少。因此,开发技术含量高、安全性好、可靠性高、耐恶劣环境能力强的球阀,满足市场的需求,具有重大的现实意义。阀体是球阀的重要部件之一,设计合理与否会直接影响整台阀门性能的好坏 [4] 。本文主要讨论球阀在高温中压过热蒸汽环境中零部件的热应力状态,并对其使用寿命进行了评估。
2. 热应力数学模型
热应力分析的数学模型如下 [5] :
1) 轴对称运动微分方程
(1)
式中,
2) 几何方程
(2)
3) 物理方程
(3)
热应力的广义胡克定律为:
(4)
3. 几何模型
球阀由全通径金属密封球阀与涡轮减速箱组成,如图1所示。
球阀由阀体、阀盖、球体、阀杆、阀座、膜片、弹簧、弹簧座、滚轮、销轴、阀杆轴套、填料、填料压套、填料压盖、支架、垫片、螺栓、螺母等主要零件组成。
涡轮减速箱由箱体、箱盖、蜗轮、蜗杆、轴承、手轮等主要零件组成。涡轮减速箱可根据现场空间和操作的需要在在安装方向上进行调整。
4. 热应力计算及分析
本文利用ANSYS软件,基于稳态温度场的计算结果,进行瞬态温度计算,然后基于瞬态温度场结果计算整个阀门系统的热应力。瞬态温度计算过程:对阀门内侧与流体接触的表面施加温度载荷,而且以50℃/h的速率增加到475℃;热应力分析:基于瞬态温度分布的结果,计算由于温度变化引起的热应力。
阀门重要零部件的热应力分布如图2~4所示,对于阀体,最大热应力达到278 MPa,但考虑到这是局部集中应力,阀体的热应力主要处于50 MPa到100 MPa之间。对于阀盖–阀盖,其热应力的大小在60 MPa~100 MPa之间;同样的,球体热应力大小在40 MPa~100 MPa之间;阀杆热应力大小在50 MPa~60 MPa之间,如图5所示;上盖和底盖热应力在80 MPa~100 MPa之间,如图6和图8所示;支架热应力在30 MPa左右,如图7所示;所有螺栓均低于50 MPa,如图9和图10所示。因此,计算结果表明所有零部件热应力均低于相应材料的许用应力,满足强度要求。
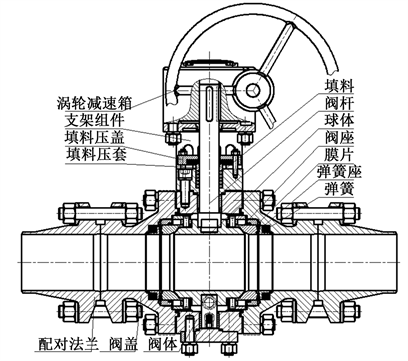
Figure 1. Structure of ball valve
图1. 球阀结构图

Figure 2. Body thermal stress distribution
图2. 阀体热应力分布

Figure 3. Bonnet-Valve Cover Thermal Stress Distribution
图3. 阀盖–阀盖热应力分布
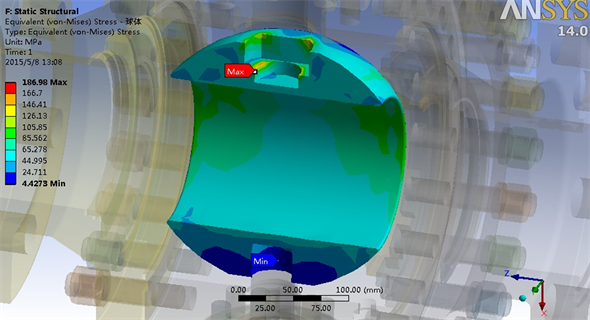
Figure 4. Ball thermal stress distribution
图4. 球体热应力分布
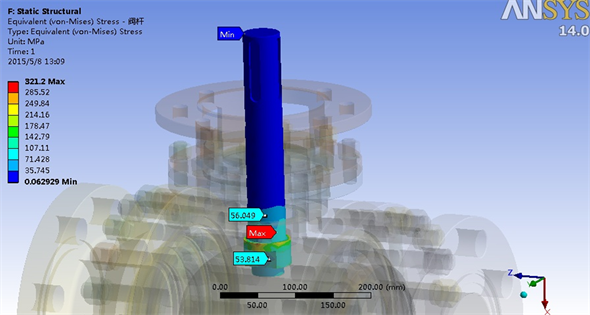
Figure 5. Valve stem thermal stress distribution
图5. 阀杆热应力分布
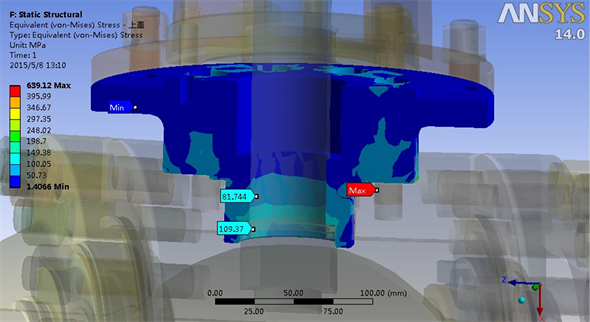
Figure 6. Top cover thermal stress distribution
图6. 上盖热应力分布
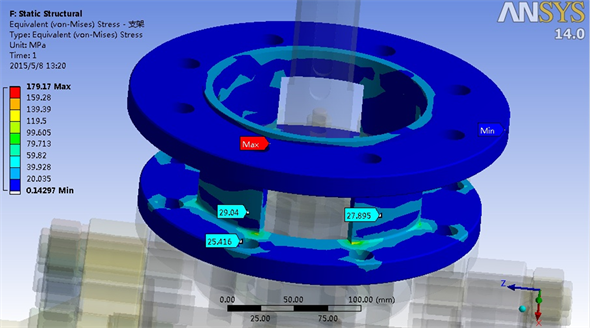
Figure 7. Bracket thermal stress distribution
图7. 支架热应力分布
5. 疲劳分析
疲劳敏感性(Fatigue Sensitivity):该疲劳敏感曲线图给出了承压壳体的寿命、损伤或安全系数在临界区域随载荷的变化情况。从图11中曲线变化可知,该阀门的理论计算寿命达到144,000次,保证了阀门
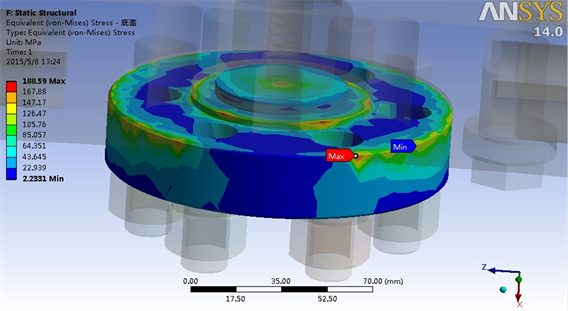
Figure 8. Bottom cover thermal stress distribution
图8. 底盖热应力分布

Figure 9. Body-bonnet connection bolt thermal stress distribution
图9. 阀体–阀盖连接螺栓热应力分布

Figure 10. Body-bottom cover connecting bolt thermal stress distribution
图10. 阀体–底盖连接螺栓热应力分布
承压边界的完整性。
6. 结论
本文通过对高温中压蒸汽系统球阀的重要零部件结构进行了热应力分析并对阀门耐压壳体进行了寿
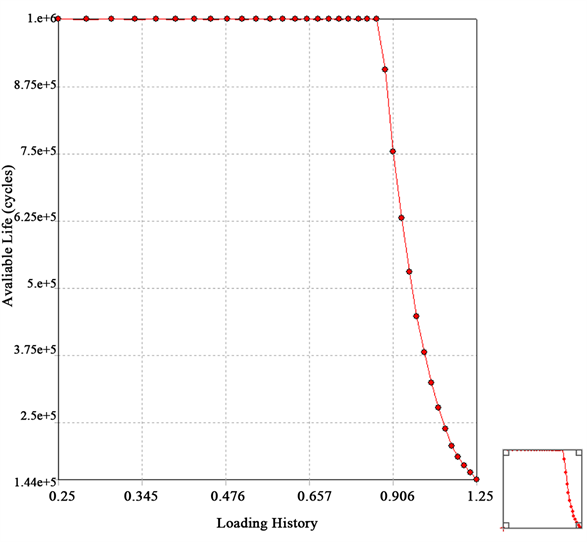
Figure 11. Fatigue sensitivity curve
图11. 疲劳敏感曲线
命评估,可以得出以下结论:
1) 阀门能够承受高温载荷,计算得到的主要承压件均低于材料的许用应力,满足强度要求。
2) 该阀门可在设计工况下启闭144,000次,保证了阀门承压边界的完整性。
基金项目
国家部委基金资助项目。
文章引用
董珠琳,刘建军,于胜剑. 高温中压蒸汽系统球阀热应力仿真计算及寿命评估
Simulation and Life Evaluation of Thermal Stress of Ball Valve in High Temperature Medium Pressure Steam System[J]. 应用物理, 2018, 08(06): 282-288. https://doi.org/10.12677/APP.2018.86037
参考文献
- 1. 唐金兰, 余佳, 等. 双向旋转变喉面流量调节阀热应力分析[J]. 推进技术, 2011, 32(4): 591-596.
- 2. 李金海, 熊滨生, 等. 微水节能热风阀阀板的热应力分析[J]. 中原工学院学报, 2009, 20(1): 5-7.
- 3. 周明钢, 董中杰. 超临界600MW汽轮机组阀门启动热应力数值分析[J]. 汽轮机技术, 2013, 55(6): 420-430.
- 4. 蒋建斐, 忻建华, 等. 660MW超临界汽轮机机组进汽阀热应力优化[J]. 热力透平, 2014, 43(4): 281-286.
- 5. 刘金梁, 刘明, 等. 阀门热应力分析与研究[J]. 阀门, 2012(2): 12-13.