Computer Science and Application
Vol.4 No.11(2014), Article
ID:14397,5
pages
DOI:10.12677/CSA.2014.411038
A Star-Tree-Structured Deterministic Small-World Network
1Department of Mathematics, Qinghai Normal University, Xining
2School of Computer Science, Qinghai Normal University, Xining
Email: houpengfeng@gmail.com, haixingzhao@yahoo.com.cn
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Sep. 28th, 2014; revised: Oct. 30th, 2014; accepted: Nov. 8th, 2014
Abstract
In the past dozen years, many probabilistic small-world networks and some deterministic smallworld networks have been proposed utilizing various mechanisms. Recently, Guo et al. [1] proposed a deterministic small-world network model by first constructing a binary-tree structure from star K1,2 by adding some edges in each iteration with a simple mechanism. In this paper, we propose a new deterministic small-world network model by constructing a binary-tree structure from a star K1,6 and then adding links between each grandfather node and its four grandson nodes for each tree in each iteration. Furthermore, we give the analytic solution to several topological characteristics, which shows that the proposed model is a small-world network.
Keywords:Small World Network, Star-Tree-Structure, Topological Characteristics

一种星–树结构的确定性的小世界网络
侯鹏锋1,赵海兴2
1青海师范大学数学系,西宁
2青海师范大学计算机学院,西宁
Email: houpengfeng@gmail.com, haixingzhao@yahoo.com.cn
收稿日期:2014年9月28日;修回日期:2014年10月30日;录用日期:2014年11月8日

摘 要
在过去的的几十年,人们运用各种机制建构了许多不确定性的和确定性的小世界网络。最近,郭世泽等人[1]通过在星图K1,2上运用一个简单的算法在每个迭代步添加一些边首次形成了一个二叉树结构的确定性的小世界网络。本文通过一个星图K1,6在每个迭代步连接每个树的各祖父节点和它的四个孙子节点,由此构建一个二叉树结构的新的确定性的小世界网络模型。此外,我们给出了一些拓扑属性的分析结果,它表明构建的模型是小世界网络。
关键词
小世界网络,星–树结构,拓扑属性

1. 引言
小世界网络描述了许多现实世界网络,如神经网络、交通运输系统、生物和化学系统、社会网络、Internet和WWW。通常地,小世界网络由三个主要的属性来描述:第一,它的平均路径长度随节点的数目对数增长,而不是随网络的规模线性地增长;第二,网络的平均节点度比较小;第三,网络有一个比较高的聚类[2] 。
学者们提出了许多描述现实世界小世界网络的模型。1998年,Watts和Strogatz[2] 提出了首个小世界网络(WS模型),它改进了小世界网络特性的许多研究。Newman和Watts[3] [4] 更进一步提出了另一个小世界网络(NW模型)。这两个经典的小世界模型都源于相同的规则环网。给定一个确定的重连概率,WS模型重连每一条边,而NW模型在未连接的节点对间添加新边。1999年,Kasturirangan提出了一个对WS模型可选择的小世界网络模型[5] ,这个模型也始于一个环网,在环网中间添加一些节点,随机地连接到主环网中的度数大的节点。此外,为了研究小世界网络的其它形成机制,Ozik、Hunt和Ott引入了一个形成小世界网络的简单的进化模型,它是连接网络上的邻近节点[6] 。
由于以上的小世界模型基于一定的概率规则连接系统中已存在的节点和新节点,因此它们都是随机的,我们不能形象地理解网络是如何形成的。为了计算、分析拓扑特性,许多学者用一些确定的方式构建无标度网络或小世界网络。Comellas等人[7] 提出了第一个确定性的小世界网络。Boettcher等人[8] 基于著名的Hanoi塔问题构建了一类确定性的小世界网络。然而,以上模型中节点数在产生过程中是固定的。基于以上的模型,许多其它类型的确定性的小世界模型被提出,比如基于prime数的[9] [10] ,基于Cayley图的[11] 。
近来,郭世泽等人[1] 提出的一个确定性的小世界网络模型,它是在星图K1,2的每对兄弟节点及每个祖父节点和它的四个孙子节点之间连边构建一个二叉树结构实现的。本文的目标是由星–二叉树通过一个简单的机制在每个迭代步添加一些边形成一个确定性的小世界模型,它的聚集系数比较高。
2. 确定性小世界网络的构建
在大多数现实网络中,节点数目经常随时间步指数增长。因此,我们在星图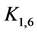 的每个叶节点附着一个二叉树得到了一个新树,它的节点数随着层数指数增长,我们称之为星–二叉树。然而,由于树中没有三角形,因此它的聚集系数等于0。为了得到比较高的聚集系数,这里我们提出一个在每个迭代步基于一个简单机制添加边的产生算法。假设t步后得到的网络为
的每个叶节点附着一个二叉树得到了一个新树,它的节点数随着层数指数增长,我们称之为星–二叉树。然而,由于树中没有三角形,因此它的聚集系数等于0。为了得到比较高的聚集系数,这里我们提出一个在每个迭代步基于一个简单机制添加边的产生算法。假设t步后得到的网络为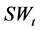 ,它的节点数为
,它的节点数为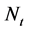 ,边数为
,边数为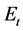 ,其中
,其中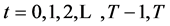 是迭代次数。假设每个节点标上一个随产生时间增加的自然数,算法如下:
是迭代次数。假设每个节点标上一个随产生时间增加的自然数,算法如下:
步骤0:初始化:使t = 0,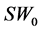 包含一个节点标记为“0”。很明显,
包含一个节点标记为“0”。很明显,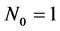 ,
, ,层数为1。
,层数为1。
步骤1:由 产生
产生 :6个标为“1”,“2”…“6”的孩子节点作为节点“0”的分支。很明显,产生了一个星图
:6个标为“1”,“2”…“6”的孩子节点作为节点“0”的分支。很明显,产生了一个星图 ,它的叶节点依次连边。因此,
,它的叶节点依次连边。因此,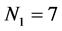 ,
,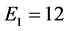 ,层数为2。
,层数为2。
步骤2:由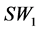 产生
产生 :在
:在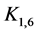 的叶节点产生两个孩子结点分支,产生了6个二叉树,在每对兄弟节点及每个新节点和根节点“0”之间连边。因此,
的叶节点产生两个孩子结点分支,产生了6个二叉树,在每对兄弟节点及每个新节点和根节点“0”之间连边。因此,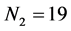 ,
,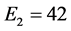 ,层数为3。
,层数为3。
步骤3:由 产生
产生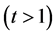
 :此步骤包含下面三个子步。
:此步骤包含下面三个子步。
步骤3.1:在 的最外层的每个节点产生两个新节点的分支,形成了一个新层。换言之,节点“
的最外层的每个节点产生两个新节点的分支,形成了一个新层。换言之,节点“ ”分别连接新产生的节点“
”分别连接新产生的节点“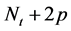 ”和“
”和“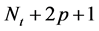 ”,其中
”,其中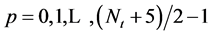 。
。
步骤3.2:在新产生层的每对兄弟节点之间添加边。换言之,节点“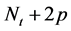 ”和“
”和“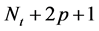 ”相连,其中
”相连,其中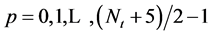 。
。
步骤3.3:对每个新产生的节点和它的祖父节点连边。换言之,每个第t层标“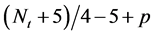 ”的节点分别与第
”的节点分别与第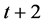 层标为“
层标为“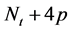 ”,“
”,“ ”,“
”,“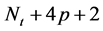 ”,“
”,“ ”的四个孙子节点连接,其中
”的四个孙子节点连接,其中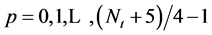 。
。
很明显,通过上面的3个子步,有 。
。
步骤4:如果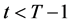 ,使
,使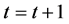 ,返回步骤3;否则,算法终止。
,返回步骤3;否则,算法终止。
以上的迭代进程重复 次,得到了一个高聚集系数的确定性的网络。事实上,我们在一定程度上模拟了家族关系。比如,兄弟节点分支对通过相同的父亲节点连接,祖父节点与它的四个孙子节点连接。图1展示了开始的四次迭代后得到的网络。由初始条件
次,得到了一个高聚集系数的确定性的网络。事实上,我们在一定程度上模拟了家族关系。比如,兄弟节点分支对通过相同的父亲节点连接,祖父节点与它的四个孙子节点连接。图1展示了开始的四次迭代后得到的网络。由初始条件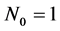 ,
,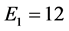 和
和 ,很容易计算
,很容易计算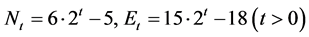 ,因此,我们得到如下的平均节点度:
,因此,我们得到如下的平均节点度:
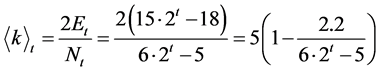 (1)
(1)
由于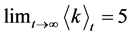 ,可以看出得到的网络是一个稀疏图,它的节点比可能有更少的连接。
,可以看出得到的网络是一个稀疏图,它的节点比可能有更少的连接。
3. 确定性小世界网络的相关特性
由于它的确定性和离散特性,上面描述的模型可以精确地解决,下面我们关注度、聚集系数和直径。
3.1. 度分布
度分布是一个网络最重要的统计特性之一。由定义,一个节点i的度等于它关联边的个数,度分布 是一个随机选择节点度为 k的概率。根据这个迭代算法,当
是一个随机选择节点度为 k的概率。根据这个迭代算法,当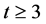 时,可以很清楚地看出构建的网络在第一层、中间层、次外层和最外层的节点对应的度分别为18,9,5,3。因此,可以得出:
时,可以很清楚地看出构建的网络在第一层、中间层、次外层和最外层的节点对应的度分别为18,9,5,3。因此,可以得出:
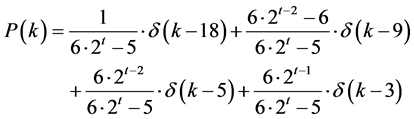 (2)
(2)
当 时,
时, ;
; 时
时 。当
。当 时,可以很容易得到下面的度分布:
时,可以很容易得到下面的度分布:
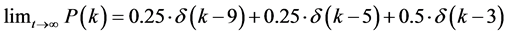 (3)
(3)
因此,构建的网络的度分布是离散的,主要对应3个度值,它与大多数小世界网络的度分布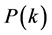 是以度k为幂指数的指数分布是不同的。
是以度k为幂指数的指数分布是不同的。

Figure 1. The first four iterations of the growth of the proposed network
图1. 构建网络增长的前四次迭代
3.2. 聚集系数和聚集度相关性
由定义,一个节点i的聚集系数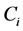 是它的
是它的 个相邻节点之间实际存在的边数
个相邻节点之间实际存在的边数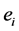 和所有可能的边数
和所有可能的边数 的比率。故
的比率。故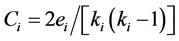 。整个网络的聚集系数是所有节点聚集系数的平均值。由于构建网络的对称性,相同度的节点具有相同的聚集系数。在迭代步t,有
。整个网络的聚集系数是所有节点聚集系数的平均值。由于构建网络的对称性,相同度的节点具有相同的聚集系数。在迭代步t,有 层。当
层。当 时,对于第一层节点,有
时,对于第一层节点,有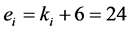 ;对于第二层节点,有
;对于第二层节点,有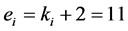 ;对于第t层节点,有
;对于第t层节点,有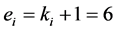 ;对于第
;对于第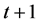 层节点,有
层节点,有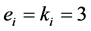 ;对于其余的中间层,有
;对于其余的中间层,有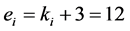 。因此,我们很容易得到下面的结果:
。因此,我们很容易得到下面的结果:
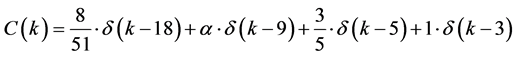 (4)
(4)
当节点位于第二层,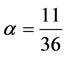 ;否则
;否则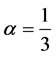 。
。
此外,由于 ,有
,有 ,因此聚集度相关性可以简单地描述为
,因此聚集度相关性可以简单地描述为 。也就是说,聚集系数和节点度之间有一个负相关性,它意味着节点的度越大,它的聚集系数越小。
。也就是说,聚集系数和节点度之间有一个负相关性,它意味着节点的度越大,它的聚集系数越小。
基于等式(4)和等式(2),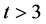 时,整个网络的平均聚集系数C计算如下:
时,整个网络的平均聚集系数C计算如下:
 (5)
(5)
由于 ,当迭代步t趋近无穷大时,C将单调减少到常数值
,当迭代步t趋近无穷大时,C将单调减少到常数值 。因此,这个网络的聚集系数是非常高的。
。因此,这个网络的聚集系数是非常高的。
3.3. 直径和平均路径长度
除了度分布和聚集系数,平均路径长度是另一个描述网络的重要参数。平均路径长度定义为网络的所有节点对的最短路径的平均值。人们发现小世界现象是最接近现实网络的,由于它表现出一个短的平均路径长度。对大多数网络模型,很难得到平均路径长度的分析值。为了证明任意节点对之间有短的距
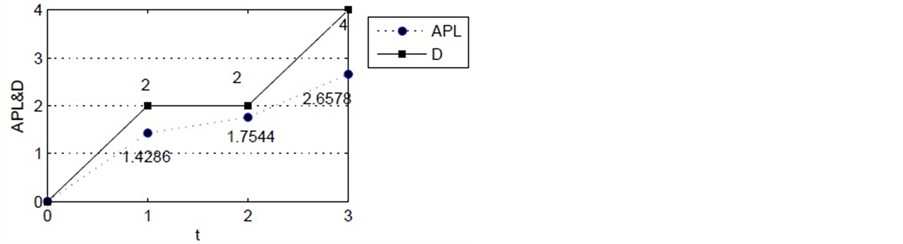
Figure 2. The APL and D versus the logarithm of the number of nodes 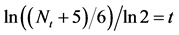
图2. 平均路径长度、直径和节点个数的对数 比较
比较
离,可以采用另一个参数直径。直径定义为网络中任意两个节点距离的最大值,它表明网络的最大传输延迟。如果一个网络的直径比较小,那么它无疑就有一个短的平均路径长度。直径在迭代步t表示为D(t)。由于网络是星树结构的,很容易看出直径总是位于非邻接树的最外层节点之间。当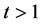 时,以节点对
时,以节点对 为例,从节点
为例,从节点 到节点
到节点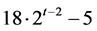 游历,如果t是偶数,最短路径包含t条边;如果t是奇数,最短路径包含
游历,如果t是偶数,最短路径包含t条边;如果t是奇数,最短路径包含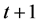 条边。因此有下面得公式:
条边。因此有下面得公式:
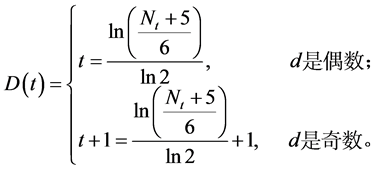 (6)
(6)
此外,直径D随节点的数目对数地增长。由于平均路径长度比直径小,因此平均路径长度应该增长的更慢。为了更清晰地展示它们的关系,图2提供了一个模拟的结果。
基于以上的讨论,我们构建的模型是稀疏的,具有高的聚集系数、短的直径和平均路径长度,它满足小世界网络的三个主要特征。因此它是一个确定性的小世界网络。
4. 结论
综上所述,我们通过在星–二叉树的每对兄弟节点及祖父节点和它的孙子节点之间添加边,提出了一个确定性的小世界模型,然后计算出了一个不小于0.7333的比较高的聚集系数,产生了一个小世界网络。我们得到了确定性模型的度分布、聚集系数、聚集度相关性和直径的分析结果,它们都很接近存在的随机小世界网络。这个模型提供了一种通过修改已存网络来产生包含特定属性的网络的方法,也可以帮助工程师进行拓扑设计和性能分析,也可以帮助我们去掉小世界现象的神秘性。
基金项目
科技部973专项(No. 2010CB334708);国家自然基金项目(No. 61164005);教育部长江学者与创新团队支持计划(No. IRT1068);青海省自然基金项目(No. 2012-Z-943)。
参考文献 (References)
- [1] Guo, S.Z., Lu, Z.M., Kang, G.Y., Chen, Z. and Luo, H. (2012) A tree-structured deterministic small-world network. IEICE Transactions on Information and Systems, E95-D.
- [2] Watts, D.J. and Strogatz, S.H. (1998) Collective dynamics of “small-world” networks. Nature, 393, 440-442.
- [3] Newman, M.E.J. and Watts, D.J. (1999) Renormalization group analysis of the small-world network model. Physics Letters A, 263, 341-346.
- [4] Newman, M.E.J. and Watts, D.J. (1999) Scaling and percolation in the small-world network model. Physical Review E, 60, 7332-7342.
- [5] Kasturirangan, R. (1999) Multiple scales in small-world network.
- [6] Ozik, J., Hunt, B.-R. and Ott, E. (2004) Growing networks with geographical attachment preference: Emergence of small worlds. Physical Review E, 69, Article ID: 026108.
- [7] Comellas, F., Ozon, J. and Peters, J.G. (2000) Deterministic small-world communication networks. Information Processing Letters, 76, 83-90.
- [8] Boettcher, S., Gongalves, B. and Guclu, H. (2008) Hierarchical regular small-world networks. Physics A: Mathematical and Theoretical, 41, Article ID: 252001.
- [9] Chandra, A.K. and Dasgupta, S. (2005) A small world network of prime numbers. Physica A, 357, 436-446.
- [10] Corso, G. (2004) Families and clustering in a natural numbers network. Physical Review E, 69, Article ID: 036106.
- [11] Xiao, W.J. and Parhami, B. (2006) Cayley graphs as models of deterministic small-world networks. Information Processing Letters, 97, 115-117.