Computer Science and Application
Vol.06 No.05(2016), Article ID:17711,11
pages
10.12677/CSA.2016.65036
On the Matching Number of Directed Triangle Trees
Mengying Li, Haixing Zhao
Computer Department, QingHai Normal University, Xining Qinghai

Received: May 4th, 2016; accepted: May 27th, 2016; published: May 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
A matching of a directed graph G is a set of some directed edges without common starting-node and end-node. K-matching of a digraph G is the matching with the k (k = 1, 2,…, n) edges; k-matching number of a graph G is the number of distinct matchings containing k (k = 1, 2,…, n) edges. The matching of a graph G refers to the number of all k-matchings. Liu and Barabasi put forward: the number of controllable nodes in directed networks is equal to the number of nodes of directed networks minus the number of edges of the maximum matching. It illustrates that the matching number and controllability of directed networks have a close connection. Thus, the research of the number of all matchings of directed networks is of applied significance. This article mainly studies the counting problems and the extremal problems on the number of matchings in a class of directed triangle trees. We investigate the calculation method and the expression of the matching number in a class of directed triangle trees with n triangles and determine the bounds for the matching number in directed triangle trees with n triangles and the correspond graphs.
Keywords:Complex Networks, Directed Tree, Directed Triangle Trees, Matching, Hosoya Index

有向三角形树的匹配数
李梦英,赵海兴
青海师范大学计算机学院,青海 西宁

收稿日期:2016年5月4日;录用日期:2016年5月27日;发布日期:2016年5月30日

摘 要
有向图G的一个匹配是由其一组没有公共起点也没有公共终点的有向边构成的集合。图G的k匹配是指含k (k = 1, 2, …, n)条有向边的匹配;图G的k-匹配数是指含k (k = 1, 2, …, n)条有向边的匹配的选择方法数;图G的匹配数指所有k-匹配数的和。刘和Barabasi等人提出:有向网络的可控节点数等于有向网络的顶点数减去最大匹配包含的边数。说明有向网络的可控性与有向网络的匹配数有着密切的联系。因此,研究有向网络的所有匹配数目具有一定的应用意义。这篇文章主要研究一类有向三角形树的所有匹配数的计数问题和极值问题。给出了一类含n个三角形的有向三角形树匹配数的计算方法,以及有向三角形树匹配数的上下界和相应的结构。
关键词 :复杂网络,有向树,有向三角形树,匹配,Hosoya指标

1. 引言
随着以互联网 [1] 为代表的网络信息技术的飞速发展,人类社会已经逐步进入了复杂网络时代。钱学森给出了复杂网络 [2] 的一个较为严格的定义:具有自相似、无标度、自组织、小世界、吸引子中部分或全部性质的网络为复杂网络。如何利用复杂网络让人们的生活更加有效,成为了人们关注的焦点。基于此,一些学者开始研究复杂网络的可控性。如果我们想要控制一个系统,我们首先要确定一个顶点集,通过在这些顶点集上输入不同的信号完全控制整个网络,我们称这些节点为驱动节点。我们特别有兴趣于:确定最小的驱动节点数 [3] ,记为ND,它可以有效地完全控制系统的动力学过程。2011年刘和Barabasi 等人 [3] 给出有向网络匹配的定义及最小输入定理:指出有向网络的可控节点数等于有向网络的顶点数减去最大匹配包含的边数,由此开启了研究复杂网络可控性的新篇章。
1971年日本化学家Haruo Hosoya [4] - [6] 介绍了基于结构描述的分子图,他命名了拓扑指标并记为Z。他用下面的方式定义了Z或Z(G):从图G中选择k条相互独立的边的方法数记为m(G, k),对所有图m(G, 0) = 1,并且m(G, 1)等于图G的边数,则:
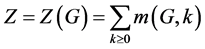
称Z或Z(G)为Hosoya指标或Hosoya拓扑指标。
本文中我们首先给出有向树、有向三角形树及有向三角形树匹配的概念,研究有向三角形树的匹配数及其相关性质。其次根据本文的主要内容给出计算一类有向三角形树匹配数的算法。
2. 基本知识
首先给出一些无向图、有向图及有向树的基本定义以及基本的符号表示。
2.1. 无向图的基本概念
一个图G = (V, E)是一个三元组 [7] ,这个三元组包含一个顶点集V(G),一个边集E(G)和一个关系,该关系使得每一条边和两个顶点(不一定是不同的点)相关联,并将这两个顶点称为这条边的端点。设边e的两个端点分别为u和v,则边e记为 ,称节点u和v在图G中邻接,记为u~v或v~u,并称节点u和v与边e关联;否则称为不邻接,记为u!~v。图G中,与节点v相关联的边的数目称为v的度,记dG(v)或d(v)。度为0的点称为孤立点,度为1的点称为悬挂点。
,称节点u和v在图G中邻接,记为u~v或v~u,并称节点u和v与边e关联;否则称为不邻接,记为u!~v。图G中,与节点v相关联的边的数目称为v的度,记dG(v)或d(v)。度为0的点称为孤立点,度为1的点称为悬挂点。
图G = (V, E)的一个匹配M [7] 是由其一组没有公共端点的不是圈的边构成的集合;M是由若干条边构成的集合,故其大小就是边的条数。图G = (V, E)的一个极大匹配是不能再通过添加边来使其变大的匹配。一个最大匹配是图G = (V, E)的所有匹配中边数达到最大值的匹配,即含边数最多的匹配。
图G = (V, E)的一条路径Pn [7] 是一个简单图,其顶点排序使得两个顶点是邻接的当且仅当它们在顶点的序列中是前后相继的。
2.2. 有向图的基本概念
一个有向图 [7] G是一个三元组,其中包含一个顶点集V(G),一个边集E(G)和一个为每有向条边分配一个有序顶点对的函数f,有序对的第一个顶点是有向边的尾部,称为有向边的起点;第二个顶点是有向边头部,称为有向边的终点;它们统称为有向边的端点。设有向边e的尾部为u,头部为v,则有向边e记为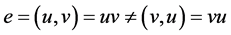 ,称节点u和v在图G中邻接,记为u~v,我们说一条有向边就是指一条从其尾部到头部的边。若令v是有向图G中的顶点,出度是以v为尾部的边的条数,记为d+(v);入度是以v为头部的边的条数,记为d-(v)。
,称节点u和v在图G中邻接,记为u~v,我们说一条有向边就是指一条从其尾部到头部的边。若令v是有向图G中的顶点,出度是以v为尾部的边的条数,记为d+(v);入度是以v为头部的边的条数,记为d-(v)。
有向图G的一个匹配M [7] 是由其一组没有公共起点也没有公共终点的有向边构成的集合。匹配M中包含的有向边的终点称为匹配节点,否则为未匹配节点。M [7] 是由若干条有向边构成的集合。故其大小就是有向边的条数。有向图G的一个极大匹配是不能再通过添加有向边来使其变大的匹配。一个最大匹配是有向图G的所有匹配中有向边数达到最大值的匹配,即含有向边数最多的匹配。
有向图G的一条途径 [8] 是由顶点vi与有向边ei交错排列的序列 ,简记为
,简记为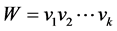 ,使得对于
,使得对于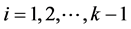 ,W中的有向边ei的尾是顶点vi、头是顶点vi+1。我们也称W为一条从v1到vk的途径。若一条途径W中任意两条有向边都不相同,则称W为迹。若一条迹中的顶点是互不相同的,则称W为路径Pn。
,W中的有向边ei的尾是顶点vi、头是顶点vi+1。我们也称W为一条从v1到vk的途径。若一条途径W中任意两条有向边都不相同,则称W为迹。若一条迹中的顶点是互不相同的,则称W为路径Pn。
刘和Barabasi等人 [3] 给出有向网络的匹配的定义:有向网络的边的子集E*称为是一个匹配集,如果E*中任意两条边都没有公共的始点,也没有公共的终点。如果一个节点是E*中某一条边的终点,该节点为匹配节点,否则为未匹配节点。
如果有向图 [9] G = (V, E)被称为有向树T = (V, E),则满足以下三个条件
1) 有且仅有一个节点的入度为0;
2) 除树根外的节点的入度为1;
3) 从树根到任一节点有一条连通的有向路。
有向图 [9] G = (V,E),在不考虑边的方向时是一棵无向树,则该有向图称为有向树。如图1。
其中顶点集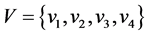 ,边集
,边集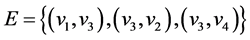 ;其中入度为0的节点称为树根,出度为0的节点称为树叶;称节点v的前驱元素为v的父节点,称v的后继元素为v的子节点。事实上,在一个无环有向图G = (V,E)中也可以定义父节点和子节点,若有向边
;其中入度为0的节点称为树根,出度为0的节点称为树叶;称节点v的前驱元素为v的父节点,称v的后继元素为v的子节点。事实上,在一个无环有向图G = (V,E)中也可以定义父节点和子节点,若有向边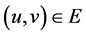 ,则称节点u是节点v的父节点,节点u是节点v的子节点。若有向边
,则称节点u是节点v的父节点,节点u是节点v的子节点。若有向边 ,则称u是v的父节点,v是u的子节点。
,则称u是v的父节点,v是u的子节点。
有向树中,入度为0的节点称为树根 [9] ,出度为0的节点称为树叶,出度不为0的节点称为分支节点,将不是根的分支节点称为内点。称从根节点到某个节点的路径长度为该节点的层或级。于是根节点是第0层节点,其子节点是第1层节点,以此类推。称与父节点在同一层的节点为堂兄弟。称节点的最大层次为树的高度或深度。

Figure 1. Directed tree G = (V; E)
图1. 有向树G = (V; E)
有向树T = (V, E) [9] 中,v∈V,由节点v及其所有后代导出的子图称为有向树T = (V, E)的子根树或子树。
有向树T = (V, E) [9] 中,若maxv∈V d+(v) = m则称T = (V, E)是有向m叉树。在m叉树T=(V, E)中,若对任意节点v都有d+(v) = m或0,则称T=(V, E)是有向完全m叉树,所有树叶节点所在的层都相同的有向完全m叉树称为有向正则m叉树或有向满m叉树。
3. 一类有向三角形树的匹配数
刘和Barabasi等人 [3] 给出了有向网络匹配的定义以及有向网络可控节点数等于顶点数减去最大匹配包含的边数的结论。自然的问题是研究有向网络的所有匹配数目。本文中主要研究有向三角形树的所有匹配数的计数问题。首先给出与有向树F和有向三角形树D相关的一些基本定义,给出一类有向三角形树匹配数的计算方法、表达式,确定有最大和最小匹配数的有向三角形树的结构,其次根据本文的主要内容给出计算一类有向三角形树匹配数的算法。
3.1. 有向树的基本定义
有向树T被称为有向树F = (V, E),则有向树T中的有向边的方向均是由上一层中的父节点指向下一层中的子节点的。如图2。
其中顶点集: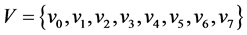 ,边集:
,边集: ;其中入度为0的节点称为树根,出度为0的节点称为树叶;若有向边(u, v)∈E,则称u是v的父节点,v是u的子节点。
;其中入度为0的节点称为树根,出度为0的节点称为树叶;若有向边(u, v)∈E,则称u是v的父节点,v是u的子节点。
有向星图F*是恰好只有一个节点出度为n-1,其余节点均为叶子节点的n个节点的有向树F。有向路Fp是节点出度为1或0的有向树F。
3.2. 有向三角形树的基本定义
有向三角形树D = (V, E)的过程为:t = 1时,以v0为根节点,以v1,v2为左右子节点,生成两条有向边v0v1,v0v2,且节点v1,v2之间生成一条有向边v1v2(第三边),这时节点{v0,v1,v2}构成一个有向三角形,记为D1;t = 2时,D1恰好包含3个节点{v0,v1,v2}∈V,在D1的任意一个节点上粘贴D1的节点v0,生成有向三角形树D2;以此类推,在有向三角形树Di的任意一个节点上,粘贴D1的节点v0,生成有向三角形树Di+1;以时间步生成有向三角形树Dn。图3是其中一种生成结果。
其中顶点集: ,边集:
,边集: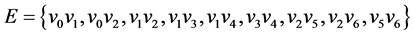 ;其中入度为0的节点称为树根,出度为0的节点称为树叶;若有向边(u, v)∈E,则称u是v的父节点,v是u的子节点。
;其中入度为0的节点称为树根,出度为0的节点称为树叶;若有向边(u, v)∈E,则称u是v的父节点,v是u的子节点。
有向三角形星图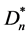 是在每一时间步都将D1的节点v0粘贴到节点v0而生成的。有向三角形路Dpn(Dpn)
是在每一时间步都将D1的节点v0粘贴到节点v0而生成的。有向三角形路Dpn(Dpn)

Figure 2. Directed tree F
图2. 有向树F

Figure 3. Directed triangle tree D3
图3. 有向三角形树D3
在每一时间步都将D1的节点v0粘贴到有向三角形树的最左(右)端的节点而生成的。
有向三角形树D的匹配数:n个三角形的有向三角形树D的边的子集E*称为是一个匹配集,如果E*中的任意两条有向边都没有公共的始点,也没有公共的终点。有向三角形树D的一个匹配是由若干条有向边构成的集合,故其大小就是有向边的条数。有向三角形树D的一个极大匹配是不能再通过添加有向边来使其变大的匹配。有向三角形树D的一个最大匹配是有向三角形树D的所有匹配中有向边数达到最大值的匹配,即含有向边数最多的匹配。有向三角形树D的k匹配是指含k条有向边的匹配;有向三角形树D的k匹配数指含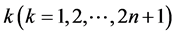 条有向边的匹配的选择方法数;有向三角形树D的匹配数指所有k匹配数的和,记为Z(D);这里规定有向三角形树D的0匹配为1,即,空图(记为O)或只包含孤立点的有向树的匹配数为1。显然图3中有向三角形树D3的1匹配数为9:v0v1,v0v2,v1v2,v1v3,v1v4,v3v4 v2v5,v2v6,v5v6;2-匹配数为28:{v0v1, v1v3},{v0v1, v1v4},{v0v1, v3v4},{v0v1, v1v2},{v0v1, v2v5},{v0v1, v2v6},{v0v1, v5v6},{v0v2, v1v3},{v0v2, v1v4},{v0v2, v3v4},{v0v2, v2v5},{v0v2, v2v6},{v0v2, v5v6},{v1v2, v3v4},{v1v2, v2v5},{v1v2, v2v6},{v1v2, v5v6},{v1v3, v3v4},{v1v3, v2v5},{v1v3, v2v6},{v1v3, v5v6},{v1v4, v2v5},{v1v4,v2v6},{v1v4, v5v6},{v3v4, v2v5},{v3v4, v2v6},{v3v4, v5v6},{v2v5, v5v6};同理,3-匹配数为36;4-匹配数为17;5-匹配数为3;有向三角形树D3的匹配数:0匹配数 + 1匹配数 + 2匹配数 + 3匹配数 + 4匹配数 + 5匹配数 = 95。
条有向边的匹配的选择方法数;有向三角形树D的匹配数指所有k匹配数的和,记为Z(D);这里规定有向三角形树D的0匹配为1,即,空图(记为O)或只包含孤立点的有向树的匹配数为1。显然图3中有向三角形树D3的1匹配数为9:v0v1,v0v2,v1v2,v1v3,v1v4,v3v4 v2v5,v2v6,v5v6;2-匹配数为28:{v0v1, v1v3},{v0v1, v1v4},{v0v1, v3v4},{v0v1, v1v2},{v0v1, v2v5},{v0v1, v2v6},{v0v1, v5v6},{v0v2, v1v3},{v0v2, v1v4},{v0v2, v3v4},{v0v2, v2v5},{v0v2, v2v6},{v0v2, v5v6},{v1v2, v3v4},{v1v2, v2v5},{v1v2, v2v6},{v1v2, v5v6},{v1v3, v3v4},{v1v3, v2v5},{v1v3, v2v6},{v1v3, v5v6},{v1v4, v2v5},{v1v4,v2v6},{v1v4, v5v6},{v3v4, v2v5},{v3v4, v2v6},{v3v4, v5v6},{v2v5, v5v6};同理,3-匹配数为36;4-匹配数为17;5-匹配数为3;有向三角形树D3的匹配数:0匹配数 + 1匹配数 + 2匹配数 + 3匹配数 + 4匹配数 + 5匹配数 = 95。
3.3. 一类有向三角形树匹配数的计算方法
设D=(V, E)是在有向完全二叉树中的每一个节点的左右子节点上,添加一条从左子节点到右子节点的有向边所得的图,它是一类特殊的有向三角形树图。下面给出这一类有向三角形树匹配数的多项式算法。
定理3.3.1设D = (V, E)是在有向完全二叉树中的每一个节点的左右子节点上,添加一条从左子节点到右子节点的有向边所得的的图,设D = (V, E)是有n个三角形的有向三角形树,v1,v2分别是有向三角形树D的根节点v0的左、右子节点,则

这里Dvi是以vi为根节点的有向三角形树;Dvi-vi是从有向三角形树Dvi中删除根节点vi形成的有向子图;
设v3,v4分别是v1的左、右子节点,则
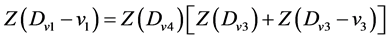
这里Dv3-v3是Dv1-v1的有向子图。
证明:用归纳法证明,n = 1时,有向三角形树D仅包含一个三角形,Z(D) = 5,定理成立。
假设对小于n个三角形的有向三角形树D定理成立。设v1,v2分别是v0 的左、右子节点,见图4。
则有向三角形树D的匹配数可分为以下两类:
第一类:不包含根节点v0的匹配,即有向子图D-v0的匹配数Z(D-v0),见图5。
第二类:恰好包含根节点v0的有向边v0v1或v0v2的匹配,即有向子图D1,D2的匹配数Z(D1),Z(D2),见图6。
因此
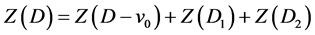
注意到有向子图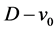 的匹配可分为以下两类:
的匹配可分为以下两类:
第一类:不包含有向边v1v2的匹配,即有向树Dv1的匹配数Z(Dv1)与有向树Dv2的匹配数Z(Dv2)的乘积,见图7。
第二类:恰好包含有向边v1v2的匹配,即有向子图D3的匹配数Z(D3),见图7。
因此

而有向子图D1的匹配可以分为以下两类:
第一类:不包含有向边v1v2的匹配,即有向子图D4的匹配数Z(D4),见图8。
第二类:恰好包含有向边v1v2的匹配,即有向子图D5的匹配数Z(D5),见图8。
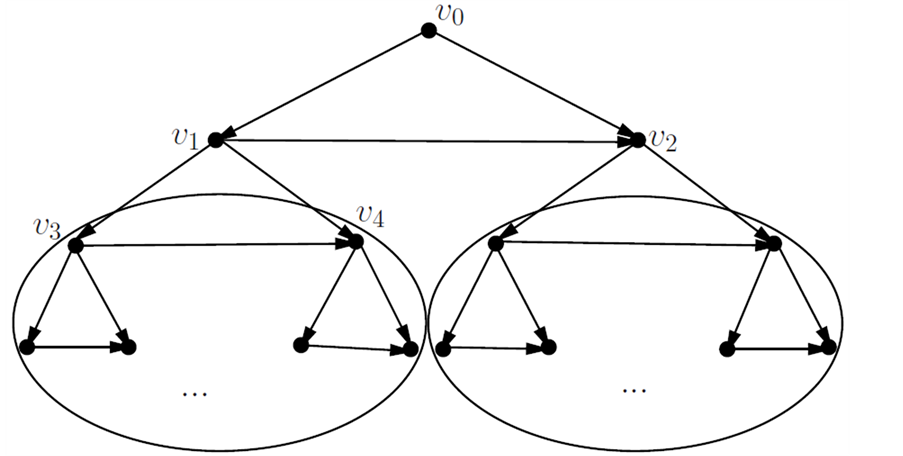
Figure 4. Directed triangle tree D
图4. 有向三角形树D
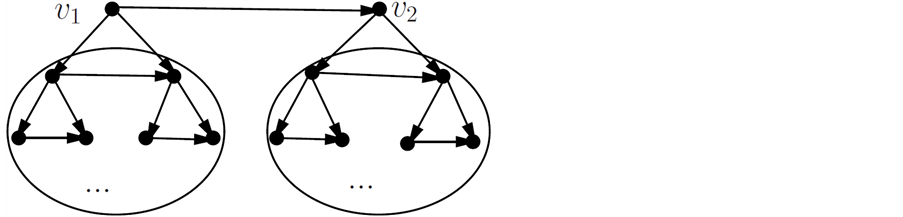
Figure 5. Directed graph D-v0
图5. 有向子图D-v0
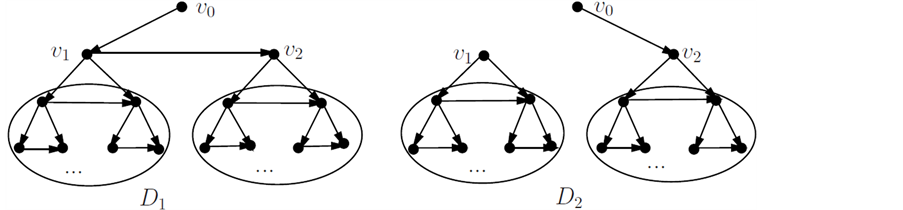
Figure 6. Directed graph D1, Directed graph D2
图6. 有向子图D1,有向子图D2

Figure 7. Directed tree Dv1, Directed tree Dv2, Directed graph D3
图7. 有向树Dv1,有向树Dv2,有向子图D3
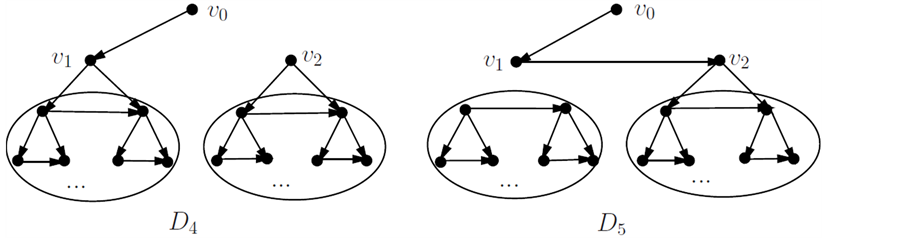
Figure 8. Directed graph D4, Directed graph D5
图8. 有向子图D4, 有向子图D5
因此
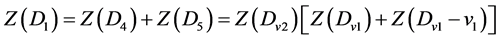 ;
;
 .
.
则有向三角形树D的匹配数
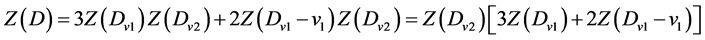
注意到有向子图 与有向子图
与有向子图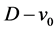 的结构相同,则
的结构相同,则

由归纳假设得:对有向三角形树Dv3,Dv4定理成立。
证毕。
定理3.3.2设D是含n个三角形的有向三角形树,则

其中 当且仅当D是有向三角形星
当且仅当D是有向三角形星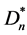 ;
;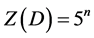 当且仅当D是有向三角形路Dpn。
当且仅当D是有向三角形路Dpn。
证明:用数学归纳法证明。N = 1时,有向三角形树D 仅包含一个三角形, ,定理成立。N = 2时,有向三角形树D包含两个三角形,这两个三角形构成的有向三角形树图有三种结构:有向三角形星图
,定理成立。N = 2时,有向三角形树D包含两个三角形,这两个三角形构成的有向三角形树图有三种结构:有向三角形星图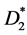 ,有向三角形路
,有向三角形路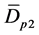 和Dp2。计算得
和Dp2。计算得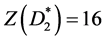 ,
, ,
,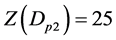 ,定理成立。
,定理成立。
假设对小于n个三角形的有向三角形树图结论成立。(1) 用数学归纳法证明右边不等式。设Dn是具有n个三角形的有向三角形树图,则Dn可以在某一个具有n-1个三角形的有向三角形树图Dn-1的任意节点与新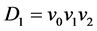 的节点v0粘贴得到。Dn和Dn-1的匹配有如下两种关系:
的节点v0粘贴得到。Dn和Dn-1的匹配有如下两种关系:
1) Dn-1的任意一个匹配和D1的任意一个匹配都没有公共始点和终点,注意到 ,此时有
,此时有

2) Dn-1的某些匹配和D1的某些匹配有公共的始点,此时有
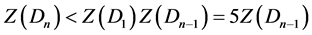
由归纳假设有
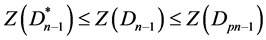
显然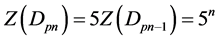 ,因此得
,因此得
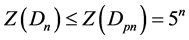
且等式成立当且仅当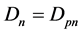 。
。
(2) 用数学归纳法证明左边不等式。设Dn可以在某一个具有n-1个三角形的有向三角形树图Dn-1的任意节点与新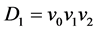 的节点v0粘贴得到,
的节点v0粘贴得到,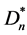 在
在 的中心与
的中心与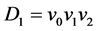 的v0粘结得到,其中
的v0粘结得到,其中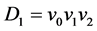 的有向边为v0v1,v0v2,v1v2。类似(1)的证明考虑
的有向边为v0v1,v0v2,v1v2。类似(1)的证明考虑 和Dn的匹配,分下面几种情况考虑:
和Dn的匹配,分下面几种情况考虑:
a)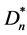 的匹配由v1v2与
的匹配由v1v2与 匹配组成,Dn的匹配由v1v2与Dn-1的匹配组成,根据归纳假设这种情形下
匹配组成,Dn的匹配由v1v2与Dn-1的匹配组成,根据归纳假设这种情形下 。
。
b) 的匹配由v0v1,v0v2,v0v1v2分别与
的匹配由v0v1,v0v2,v0v1v2分别与 三角形的第三边生成的匹配组成,Dn的匹配由v0v1,v0v2,v0v1v2分别与Dn-1三角形的第三边生成的匹配组成,这种情形下他们匹配数相等。
三角形的第三边生成的匹配组成,Dn的匹配由v0v1,v0v2,v0v1v2分别与Dn-1三角形的第三边生成的匹配组成,这种情形下他们匹配数相等。
c)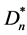 的匹配只能是v0v1,v0v2,v0v1v2,或者是
的匹配只能是v0v1,v0v2,v0v1v2,或者是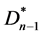 包含中心点v0的匹配,Dn的匹配由v0v1,v0v2,v0v1v2,或者Dn-1三角形的非第三边生成的匹配组成,或者由v0v1,v0v2,v0v1v2,和Dn-1中与v0不相交的Dn-1三角形的非第三边生成的匹配组成,这种情形下
包含中心点v0的匹配,Dn的匹配由v0v1,v0v2,v0v1v2,或者Dn-1三角形的非第三边生成的匹配组成,或者由v0v1,v0v2,v0v1v2,和Dn-1中与v0不相交的Dn-1三角形的非第三边生成的匹配组成,这种情形下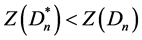 。
。
由以上讨论得:

且等式成立当且仅当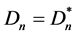 。下面计算
。下面计算 。
。
根据定理3.3.1设含n个三角形的有向三角形星图 的中心节点为
的中心节点为 是v0的邻居节点,见图9,则有向三角形星图的匹配可分为以下两类:
是v0的邻居节点,见图9,则有向三角形星图的匹配可分为以下两类:
第一类:不包中心节点v0的匹配,即有向子图 的匹配数
的匹配数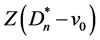 ,见图9。
,见图9。
第二类:恰好包含中心节点v0的有向边v0vi(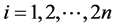 )$的匹配,即有向子图
)$的匹配,即有向子图 (
(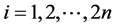 )的匹配数
)的匹配数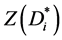 ,见图10。
,见图10。
如图10所示,共有n个有向子图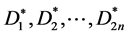 ,因此
,因此
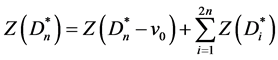
注意到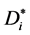 的每一个匹配必须包括有向边v0vi,当包含的有向边v0vi是v0的右节点时,
的每一个匹配必须包括有向边v0vi,当包含的有向边v0vi是v0的右节点时,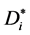 的匹配数
的匹配数

当包含的有向边v0vi是v0左节点时,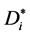 的匹配数
的匹配数

而有向三角形星图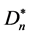 左节点数等于右节点数等于n。从
左节点数等于右节点数等于n。从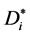 的一个k-匹配中删除左节点得到
的一个k-匹配中删除左节点得到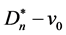 的一个(k-1)-匹配,反之在
的一个(k-1)-匹配,反之在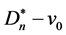 的(k-1)-匹配中添加左节点得到
的(k-1)-匹配中添加左节点得到 的一个k-匹配,
的一个k-匹配,
则有
 所以
所以

Figure 9. Directed triangle star graph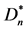 , Directed graph
, Directed graph 
图9. 有向三角形星图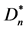 ,有向子图
,有向子图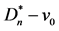
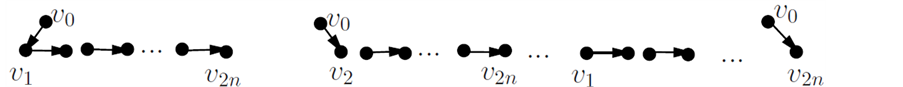
Figure 10. Directed graph 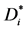
图10. 有向子图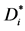
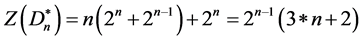
证毕。
3.4. 有向三角形树匹配数的算法
本小节中,我们给出有向三角形树匹配数的算法。
设D = (V, E)是在有向完全二叉树中的每一个节点的左右子节点上,添加一条从左子节点到右子节点的有向边所得的图,设Dn = (V, E)是包含n个三角形的有向三角形树,输出Z(Di)值。假设D0表示只含有一个节点的有向图,Dvl和Dvr分别表示Dv的左、右子图。
开始
 ,
, 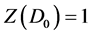 ,
, 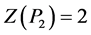
For each 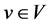 bottom up do
bottom up do
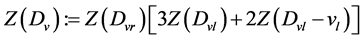

显然,该算法的时间复杂度为 。
。
4. 结论与展望
本文中我们给出了有向网络中一类有向三角形树匹配数的计算方法和计算表达式。得出:有向三角形路Dpn的匹配数最大,有向三角形星图 的匹配数最小。有向三角形树的匹配数与以其左右端子节点为顶点的有向三角形的数目密切相关:有向三角形树中,以左端子节点为顶点的有向三角形的数目越多,有向三角形树的匹配数越小;有向三角形树中,以右端子节点为顶点的有向三角形的数目越多,有向三角形树的匹配数越大。而刘和Barabasi等人有结论:有向路最易控制,即:需要的输入最少;有向星图最难控制,即:需要的输入最多;那么能否得出:有向三角形树的匹配数越大,有向三角形树越容易控制的结论;或者在什么条件下,有向三角形树的匹配数越大,有向三角形树可控制性越好,是值得思考的问题。
的匹配数最小。有向三角形树的匹配数与以其左右端子节点为顶点的有向三角形的数目密切相关:有向三角形树中,以左端子节点为顶点的有向三角形的数目越多,有向三角形树的匹配数越小;有向三角形树中,以右端子节点为顶点的有向三角形的数目越多,有向三角形树的匹配数越大。而刘和Barabasi等人有结论:有向路最易控制,即:需要的输入最少;有向星图最难控制,即:需要的输入最多;那么能否得出:有向三角形树的匹配数越大,有向三角形树越容易控制的结论;或者在什么条件下,有向三角形树的匹配数越大,有向三角形树可控制性越好,是值得思考的问题。
基金项目
本文受科技部973专项(No. 2010CB334708)、国家自然基金项目(No. 61164005)、教育部长江学者与创新团队支持计划(No. IRT1068)、国家自然科学资金项目(批准号:11551002)、青海省自然基金项目(No. 2012-Z-943)资助。
文章引用
李梦英,赵海兴. 有向三角形树的匹配数
On the Matching Number of Directed Triangle Trees[J]. 计算机科学与应用, 2016, 06(05): 292-302. http://dx.doi.org/10.12677/CSA.2016.65036
参考文献 (References)
- 1. 汪小帆, 李翔, 陈关荣. 网络科学导论[M]. 北京: 高等教育出版社, 2012.
- 2. 郭世泽, 陆哲明. 复杂网络基础理论[M]. 北京: 科学出版社, 2012.
- 3. Liu, Y.Y., Slotine, J.J. and Barabasi, A.L. (2011) Controllability of Complex Networks. Nature, 473, 167-173. http://dx.doi.org/10.1038/nature10011
- 4. 陈关荣. 复杂动态网络环境下控制理论遇到的问题与挑战[J]. 自动化学报. 2013, 39(4): 312-321.
- 5. Wagner, S. (2008) Extremal Trees with Respect to Hosoya Index and Merri-field-Simmons Index. MATCH Communications in Mathematical and in Computer Chemistry, 59, 203-216.
- 6. Wagner, S. and Gutman, I. (2010) Maxima and Minima of the Hosoya Index and Merrifield-Simmons Index A Survey of Result and Techniques. Acta Applicandae Mathematicae, 112, 323-346. http://dx.doi.org/10.1007/s10440-010-9575-5
- 7. West, D.B., 著. 图论导引[M]. 李建中, 骆吉洲, 译. 北京: 机械工业出版社, 2005.
- 8. Jogen, B.J. and Gutin, G., 著. 有向图理论, 算法及其应用[M]. 姚兵, 张忠辅, 译. 北京: 科学出版社, 2009.
- 9. 邓辉文. 离散数学[M]. 北京: 清华大学出版社, 2013.