基于LMS的多智能体系统变步长自调优一致性 Variable Step Self-Tuning Consensus of Multi-Agent Systems with Least Mean Squares Method

doi:10.12677/CSA.2018.86097

Computer Science and Application
Vol.08 No.06(2018), Article ID:25620,11 pages
10.12677/CSA.2018.86097

Variable Step Self-Tuning Consensus of Multi-Agent Systems with Least Mean Squares Method

Zongting Han, Xianxiang Wu, Xiangyan Hu, Baolong Guo, Xi Chen

●How to Cite this Article

School of Aerospace Science and Technology, Xidian University, Xi’an Shannxi

Received: Jun. 4^th, 2018; accepted: Jun. 20^th, 2018; published: Jun. 27^th, 2018

ABSTRACT

This paper considers the consensus problem in discrete time multi-agent systems. By using variable step particle swarm algorithm, the coupling parameters among agents are locally self-tuned by least-mean square (LMS) algorithm, without using any global information. In this process, each agent minimizes a local cost function dependent on the error between the agent state and the average of neighbors’ states. Provided that the network graph is strongly connected, it is shown that for each agent, the sequence of coupling parameters is convergent, and all agent states converge toward the same constant value. Finally, the proposed algorithm is verified by simulation under different topologies.

Keywords:Multi-Agent Systems, Consensus, Self-Tuning, Least Mean Squares Method

基于LMS的多智能体系统变步长自调优一致性

韩宗亭，吴宪祥，呼香艳，郭宝龙，陈曦

西安电子科技大学空间科学与技术学院，陕西西安

收稿日期：2018年6月4日；录用日期：2018年6月20日；发布日期：2018年6月27日

摘要

研究了离散时间多智能体系统中的一致性问题。在不使用任何全局信息的情况下，将粒子群的变步长算法应用到最小均方(LMS)算法中进行多智能体局部自调，实现了多智能体的一致性。在这个过程中，网络模型的代价函数取决于智能体的状态和邻居状态平均值之间的误差。同时证明了网络图强连通的情况下，所有的智能体状态将达到一致性。最后，通过在不同拓扑结构下的仿真实例对提出的算法进行验证。

关键词 :多智能体系统，一致性，自调优，最小均方算法

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

近年来，多智能体系统的协调控制问题受到了系统与控制领域专家学者的广泛关注。在多智能体系统网络中，一致性问题作为协调控制的代表性问题，也是其它分布式控制和估计的研究基础。系统达到一致性，也就是多智能体系统中每个智能体的状态在一致性协议或者算法的控制下渐进地或者在有限时间内达到相同的数值。随着多智能体协调控制的研究深入，一致性问题已经成为当前研究的热点问题，在理论和实际的应用方面都取得了很多的成果。它是多智能体系统的分布式控制研究中的基本问题之一，在交汇问题、编队控制、传感器网络的信息融合等方面有广泛应用 [1] - [10] 。

一致性理论的早期研究始于管理科学，分布式计算以及在自然界中出现的蜂群、鸟群和鱼群等常见的集群行为。在过去的二十年中，大量的论文涵盖了群集和分布式编队、分布式优化和估计、通信和传感器网络、耦合振荡器同步问题等方面的问题。2013年，Cao等人对近年来在多智能体协调方面的进展进行了较为全面的综述 [11] 。2006年，Zhou，Lu等人提出动态网络自适应一致性，作者假设整个自治网络的解是已知的，并且每个智能体使用全局信息作为智能体状态跟踪的参考，局部控制输入与智能体状态与此参考状态之间的误差成正比，并且证明了这个误差收敛到零 [12] 。2008年，Zhou，Lu等人在复杂网络中假设同步解决方案是已知的或有限制性的，得出了相似的结果 [13] 。2009年，DeLellis等人证明了全局同步依赖于自适应变化的耦合增益施加的循环条件。要求收益矩阵依赖于耦合半负定时刻 [14] 。2009年，Das等人考虑了每个智能体都必须跟踪已知或估计的领导者轨迹的问题。在未知参数和已知基函数的基础上，用一个中立的网络结构来表示非线性动力学 [15] 。2012年，Yu等人对领导者的动力学进行了类似的参数化。领导者的轨迹是全局信息，智能体间的耦合参数是一个非自适应的，它的值对于网络的所有节点都是相同的 [16] 。2013年，Li等人提出了连续时间自适应一致性问题的研究。作者分析了无向图，并假设已知输入增益对所有智能体都是相同的。证明了每个智能体的状态都收敛于所有智能体状态的平均值 [17] 。2015年，Miloje等人提出了多智能体系统的自适应一致性协议，不应用任何全局信息，应用定步长的自适应一致性算法，最后证明了每个智能体的状态都趋于所有智能体初始状态的平均值 [18] 。

总的来说，上述的研究工作对多智能体一致性的发展做出了有益的理论和实践探索。但是也存在一定的问题：一方面，需要考虑多智能体的状态到达一致性的时间问题，比如加快智能体的收敛速度；另一方面，在切换拓扑网络中的应用需要进行验证。

针对上述问题，我们在Miloje等人提出的多智能体自适应一致性协议的基础之上，提出了一种基于LMS的变步长自调优一致性协议。我们考虑了有向图拓扑，在不使用任何全局信息的情况下，每个智能体都通过最小化其本地代价函数和基于变步长LMS的参数估计器来生成耦合系数的值。代价函数等于智能体状态与其邻居状态平均值之间的局部误差的平方。结果表明，基于LMS的变步长自调优一致性算法是收敛的，所有的智能体状态都趋于一致的值。

2. 预备知识以及问题描述

2.1. 图论基础

在多智能体系统一致性问题的研究中，图论是非常重要的分析工具。通常，用记号 $G = {V, E, A}$ 表示一个加权的有向图。其中， $V = {v_{1}, v_{2}, \dots, v_{n}}$ 表示具有n个节点的节点集合，它的边集合 $E \subseteq V \times V$ ，节点的下标集合 $I = {1, 2, \dots, n}$ ；邻接矩阵 $A = [a_{i j}] \in R^{n \times n}$ ，当有向边 $(v_{i}, v_{j}) \in E$ 时，表示节点 $v_{j}$ 可以获得 $v_{i}$ 的信息，此时 $a_{i j} > 0$ ；否则， $a_{i j} = 0$ [19] 。

定义节点i的邻居集合： $N_{i} = {j : a_{i j} > 0}$ 。

矩阵 $D = d i a g {d_{i}, i = 1, 2, \dots, n}$ ， $d_{i} = \sum_{j = 1}^{n} a_{i j}$ 为矩阵A的第i行元素之和，称为节点i的出度，矩阵 $L = D - A$ 为图G的拉普拉斯矩阵 [20] 。

最小均方算法简称LMS算法，是一种最陡下降算法的改进算法，是在维纳滤波理论上运用速下降法后的优化延伸，最早是由Widrow和Hoff提出来的。LMS算法是一种随机梯度算法。它以系统均方误差为代价函数，利用随机估计值代替最速下降法中的梯度向量，在统计意义上以最速下降方向收敛到Wiener解。其具有计算复杂程度低、在信号为平稳信号的环境中收敛性好、其期望值无偏地收敛到维纳解和利用有限精度实现算法时的平稳性等特性，使LMS算法成为自适应算法中稳定性最好、应用最广的算法 [21] 。在本文中应用最小均方算法。

2.2. 问题描述

考虑一组用离散时间积分器来表示的N个智能体：

$x_{i} (t + 1) = x_{i} (t) + β_{i} u_{i} (t), i = 1, \dots, N$ (1)

$x_{i} (t) \in R$ ， $u_{i} (t) \in R$ 分别表示智能体在离散时间 $t = 0, 1, 2, \dots$ 时的状态和控制输入。 $β_{i}$ 表示第i个智能体的输入增益。假设 $β_{i}$ 的符号已知，但是它的大小是一个未知数。公式(1)可以被视为一组连续时间多智能体系统的离散版本 [18] 。

在本文中，考虑以下简单的一致性协议：

$u_{i} (t) = \sum_{j \in N_{i}} θ_{i j} (t) (x_{j} (t) - x_{i} (t))$ (2)

$θ_{i j} (t)$ 是控制参数，也是要进行估计的数值，以便智能体的状态 $x_{i} (t)$ 收敛到相同的值。例如，

$\lim_{t \to \infty} x_{i} (t) = x_{c}, \forall i \in V, x_{c} \in R$ (3)

$x_{c}$ 为多智能体系统的状态变量达到一致的数值。在本文中，提出了基于LMS的变步长算法自适应地调整参数 $θ_{i j} (t)$ 。定义参数向量：

$θ_{i} {(t)}^{T} = [θ_{i 1} (t) l_{i 1}, \dots, θ_{i N} (t) l_{i N}], \forall i \in v$ (4)

这里的 $l_{i j}$ 是指示函数，定义如下：

$l_{i j} = {\begin{cases} 1 j \in N_{i} \\ 0 其他 \end{cases}$

所以(2)中的 $u_{i} (t)$ 可以写为如下的形式

$u_{i} (t) = θ_{i} {(t)}^{T} φ_{i} (t)$ (5)

$φ_{i} (t)$ 是信号向量，定义如下：

$φ_{i} {(t)}^{T} = [ε_{i 1} (t) l_{i 1}, \dots, ε_{i N} (t) l_{i N}]$ (6)

其中：

$ε_{i j} (t) = x_{j} (t) - x_{i} (t)$ (7)

由于 $β_{i}$ 是未知的，智能体i将会自调整参数向量 $θ_{i} (t)$ ，使得下面的代价函数最小化：

$J_{i} (θ_{i}) = \frac{1}{2} {(x_{i} (t + 1) - {\bar{x}}_{i} (t + 1))}^{2}$ (8)

这里的 ${\bar{x}}_{i} (t + 1)$ 是第i个智能体邻居状态的平均值（也包含其自身的值）

${\bar{x}}_{i} (t + 1) = \frac{1}{1 + N} \sum_{j \in N_{i}} x_{j} (t), {\bar{N}}_{i} = N_{i} \cup {i}$ (9)

其中N是 $N_{i}$ 中元素的个数。

假设 $β_{i}$ 的符号是已知的，参数向量 $θ_{i} (t)$ 可以通过使用以下归一化LMS算法来估计：

$θ_{i} (t + 1) = θ_{i} (t) - μ_{i} sgn (β_{i}) \frac{φ_{i} (t) e_{i} (t + 1)}{r_{i} (t)}$ (10)

其中：

$r_{i} (t) = 1 + {‖ φ_{i} (t) ‖}^{2}$ (11)

$e_{i} (t + 1) = x_{i} (t + 1) - {\bar{x}}_{i} (t + 1)$ (12)

这里的 ${\bar{x}}_{i} (t + 1)$ 由公式(9)定义。在公式(10)中， $μ_{i} > 0$ 是步长参数，提出的这个算法的步长是改变的，在每次的迭代过程中，改变这个参数，加快收敛的速度。 $sgn (β_{i})$ 是 $β_{i}$ 的符号。公式(10)从任意初始条件 $θ_{i} (0)$ 开始迭代。将 $u_{i} (t)$ 从公式(5)中代入公式(1)中可以得到：

$x_{i} (t + 1) = x_{i} (t) + β_{i} θ_{i} {(t)}^{T} φ_{i} (t)$ (13)

由公式(8)给出的 $J_{i} (θ_{i})$ 对 $θ_{i} (t)$ 的梯度是：

$\frac{\partial J_{i} (θ_{i})}{\partial θ_{i} (t)} = e_{i} (t + 1) \frac{\partial x_{i} (t + 1)}{\partial θ_{i} (t)} = β_{i} φ_{i} (t) e_{i} (t + 1)$ (14)

其中 $e_{i} (t + 1)$ 由公式(12)定义。因此公式(10)中的第二项等于公式(8)的负梯度并进行规范化，而 $β_{i}$ 被替换为其符号标示。

公式(13)可以写成如下的紧凑的形式：

$x (t + 1) = W (t) x (t)$ (15)

这里的 $x (t)$ 是：

$x {(t)}^{T} = [x_{1} (t), x_{2} (t), \dots, x_{N} (t)]$ (16)

而 $W (t) \in R^{N \times N}$ 是耦合权重矩阵，定义如下:

$W (t) = [w_{i j}], w_{i j} (t) = {\begin{cases} β_{i} θ_{i j} (t), j \in N_{i} \\ 1 - \sum_{K \in N_{i}} β_{i} θ_{i j} (t), j = i \\ 0, 其他 \end{cases}$ (17)

2.3. 相关证明

假设图G是强连通的，且对所有的 $i = 1, 2, \dots, N$ ，公式(10)中的步长 $μ_{i}$ 是可变的，并且步长 $μ_{i}$ 满足 $μ_{i} < 2 / β_{i \max}$ 。

由公式(9)给出的 ${\bar{x}}_{i} (t + 1)$ 可以写成：

${\bar{x}}_{i} (t + 1) = a_{i}^{T} x (t)$ (18)

这里的 $x (t)$ 由公式(16)定义的。

$a_{i}^{T} = [a_{i 1}, \dots, a_{i N}], a_{i j} = {\begin{cases} \frac{1}{1 + N_{i}} j \in N_{i}, j = i \\ 0 其他 \end{cases}$ (19)

定义：

$e {(t)}^{T} = [e_{i} (t), \dots, e_{N} (t)]$ (20)

从公式(12) (16) (18)可以得到：

$x (t + 1) = A x (t) + e (t + 1)$ (21)

矩阵 $A \in R^{N \times N}$ ， $A = [a_{i j}]$ 中的 $a_{i j}$ 是由公式(19)中定义。注意到A是具有正对角元素的随机矩阵。由于假设图是强连通的，非负矩阵A是不可约的，因此，矩阵A在 $λ_{1} = 1$ 处，只有一个特征值，其他的特征值 $λ_{i}, 2 \leq i \leq N$ ，满足 $| λ_{i} | < 1$ 。 $l = {(1, \dots, 1)}^{T}$ 是对应于 $λ_{i} = 1$ 的右特征向量。让 $y_{A}$ 的作为矩阵A对应于特征值 $λ_{1}$ 的左特征向量并且标准化，得到 $y_{A}^{T} l = 1$ 。因此，矩阵A可以分解为：

$A = A_{1} + l y_{A}^{T}, l t_{A}^{T} = 1$ (22)

其中 $A_{1} l = 0, y_{A}^{T} A_{1} = 0$ ，并且 $A_{1}$ 的谱半径满足 $ρ (A_{1}) < 1$ 。把(22)带入(21)可以得到：

$x (t + 1) = A_{1} x (t) + l y_{A}^{T} x (t) + e (t + 1)$ (23)

定义：

$H (q^{- 1}) = {(I - q^{- 1} A_{1})}^{- 1}$ (24)

这里的 $q^{- 1}$ 是单位延迟算子。由于 $A_{1} l = 0$ 可以得到 $H {(q)}^{- 1} l = (I + \sum_{k = 1}^{\infty} q^{- k} A_{1}^{k}) l = l$ 。再由公式(23)可以得到：

$x (t + 1) = l y_{A}^{T} x (t) + H (q^{- 1}) e (t + 1)$ (25)

让

$ϕ_{i} (t) = x (t) - x_{i} (t) l, i \in v$ (26)

由公式(25) (26)可以得到：

$ϕ_{i} (t + 1) = l y_{A}^{T} (x (t) - l x_{i} (t)) + l y_{A}^{T} l x_{i} (t) - l x_{i} (t + 1) + H (q^{- 1}) e (t + 1)$ (27)

由于 $y_{A}^{T} l = 1$ ，因此公式(27)可以写为：

$ϕ_{i} (t + 1) = l y_{A}^{T} ϕ_{i} (t) + l [x_{i} (t) - x_{i} (t + 1)] + H (q^{- 1}) e (t + 1)$ (28)

公式(9)可以写成：

${\bar{x}}_{i} (t + 1) = x_{i} (t) + b_{i}^{T} ϕ_{i} (t)$ (29)

其中 $b_{i}$ 为：

$b_{i}^{T} = [b_{i 1}, \dots, b_{i N}], b_{i j} = {\begin{cases} \frac{1}{1 + N_{i}} j \in N_{i} \\ 0 其他 \end{cases}$ (30)

然后由公式(12)给出的误差 $e_{i} (t + 1)$ 可以表示为：

$e_{i} (t + 1) = x_{i} (t + 1) - x_{i} (t) - b_{i}^{T} ϕ_{i} (t)$ (31)

通过把公式(31)的 $x_{i} (t + 1) - x_{i} (t)$ 代入公式(28)，可以得到下式：

$ϕ_{i} (t + 1) = Q_{i} ϕ_{i} (t) - l e_{i} (t + 1) + H (q^{- 1}) e (t + 1)$ (32)

其中：

$Q_{i} = l {(y_{A} - b_{i})}^{T}$ (33)

$b_{i}^{T} = [b_{i 1}, \dots, b_{i N}], b_{i j} = {\begin{cases} \frac{1}{1 + N_{i}} j \in N_{i} \\ 0 其他 \end{cases}$ (34)

公式(33)中的矩阵 $Q_{i}$ 的秩为1，它唯一的非零特征值为：

$ρ_{1} = l^{T} (y_{A} - b_{i}) = 1 - l^{T} b_{i} = 1 - \sum_{k = 1}^{N} b_{i k} = 1 - \frac{N_{i}}{1 + N_{i}} < 1$ 因此存在正常数 $c_{0}$ ，使得对于所有的 $k \geq 0$ ， $‖ Q_{i}^{k} ‖ \leq c_{0} ρ_{1}^{k}, 0 < ρ_{1} < 1$ 。

从公式(32)可以得到：

$ϕ_{i} (t + 1) = Q_{i}^{t + 1} ϕ_{i} (0) + \sum_{k = 0}^{t} Q_{i}^{t - k} [H (q^{- 1}) e (k + 1) - l e_{i} (k + 1)]$ (35)

可以得到：

${‖ ϕ_{i} (t + 1) ‖}^{2} \leq c_{1} ρ_{1}^{k} + c_{2} \sum_{k = 0}^{t} ρ_{1}^{t - k} {‖ e (k + 1) ‖}^{2}$ (36)

其中， $c_{1}$ ， $c_{2}$ 均为常数。式(36)两边从 $t = 0$ 到 $t = n$ 两边求和得到下式：

$\sum_{t = 0}^{n} {‖ ϕ_{i} (t + 1) ‖}^{2} \leq c_{1} + c_{2} \sum_{t = 0}^{n} {‖ e (t + 1) ‖}^{2}, \forall n \geq 0$ (37)

由公式(6)和公式(18)得到 ${\bar{x}}_{i} (t + 1) = x_{i} (t) + a_{i}^{T} φ_{i} (t)$ ，再结合公式(12)和公式(13)可以得到推出如下公式：

$e_{i} (t + 1) = {\tilde{θ}}_{i} (t) φ_{i} (t)$ (38)

$e_{i} (t + 1)$ 由公式(12)定义，并且：

${\tilde{θ}}_{i} (t) = β_{i} θ_{i} (t) - a_{i}$ (39)

再结合公式(10)得到：

${\tilde{θ}}_{i} (t + 1) = {\tilde{θ}}_{i} (t) - \frac{μ_{i} | β_{i} |}{r_{i} (t)} φ_{i} (t) e_{i} (t + 1)$ (40)

将公式(40)两边平方后得到：

$V_{i} (t + 1) = V_{i} (t) - \frac{2 μ_{i} | β_{i} |}{r_{i} (t)} {\tilde{θ}}_{i} (t) φ_{i} (t) e {}_{i}{(t + 1)} + \frac{{(μ_{i} β_{i})}^{2}}{r_{i} (t)} \cdot \frac{φ_{i} {(t)}^{2}}{r_{i} (t)} e_{i} {(t + 1)}^{2}$ (41)

这里的 $V_{i} (t) = {‖ {\tilde{θ}}_{i} (t) ‖}^{2}$ ，把公式(38)中的 ${\tilde{θ}}_{i} (t) φ_{i} (t)$ 带入到公式(41)，并且由公式(11) $r_{i} (t) = 1 + {‖ φ_{i} (t) ‖}^{2}$ 可以得到 $({‖ φ_{i} (t) ‖}^{2} / r_{i} (t)) \leq 1$ ，可以得到：

$V_{i} (t + 1) \leq V_{i} (t) - 2 μ_{i} | β_{i} | (1 - \frac{μ_{i} | β_{i} |}{2}) \sum_{t = 0}^{n} \frac{e_{i} {(t + 1)}^{2}}{r_{i} (t)}$ (42)

把公式(42)的两边从 $t = 0$ 到 $t = n$ 进行求和，可以得到下式：

$V_{i} (n + 1) + 2 μ_{i} | β_{i} | (1 - \frac{μ_{i} | β_{i} |}{2}) \sum_{t = 0}^{n} \frac{e_{i} {(t + 1)}^{2}}{r_{i} (t)} \leq V_{i} (0)$ (43)

由于 $μ_{i} | β_{i} | > 0$ ，并且开始的假设成立，所以 $μ_{i} | β_{i} | < 2$ 。因此，对于所有的 $n \geq 0$

$\sum_{t = 0}^{n} \frac{e_{i} {(t + 1)}^{2}}{r_{i} (t)} \leq c_{3} < \infty, i \in v$ (44)

其中 $c_{3}$ 是常数。

定义：

$\bar{r} (t) = \sum_{i = 1}^{N} \max_{1 \leq τ \leq t} r_{i} (τ)$ (45)

可以由公式(44)得到：

$\sum_{t = 0}^{n} \frac{{‖ e (t + 1) ‖}^{2}}{\bar{r} (t)} \leq c_{4} \leq \infty$ (46)

其中， $c_{4}$ 是常数， $e (t)$ 由公式(20)定义。如果 ${\bar{r} (t)}, t \geq 0$ 是一个有界的序列，则由公式(46)可以得到：

$\sum_{t = 0}^{n} {‖ e (t + 1) ‖}^{2} \leq c_{5} < \infty$ (47)

其中， $c_{5}$ 为常数。而如果 $\lim_{t \to \infty} \bar{r} (t) = + \infty$ ，则由克罗内克引理可以得到：

$\lim_{n \to \infty} \frac{1}{\bar{r} (n)} {‖ e (t + 1) ‖}^{2} = 0$ (48)

由公式(6)和公式(26)可以得到 $‖ φ_{i} (t) ‖ \leq ‖ ϕ_{i} (t) ‖$ ，再应用公式(11) (37) (45)可以得到：

$\bar{r} (n) \leq c_{6} + c_{7} \sum_{t = 0}^{n} {‖ e (t + 1) ‖}^{2}$ (49)

其中， $c_{6}$ 和 $c_{7}$ 均为常数。由公式(48) (49)得到：

$\sum_{t = 0}^{n} {‖ e (t + 1) ‖}^{2} \leq c_{8} < \infty$ (50)

其中， $c_{8}$ 为常数。由公式(37)(47)以及 $‖ φ_{i} (t) ‖ \leq ‖ ϕ_{i} (t) ‖$ 得到：

$\sum_{t = 0}^{n} {‖ φ_{i} (t) ‖}^{2} \leq \sum_{t = 0}^{n} {‖ ϕ_{i} (t) ‖}^{2} \leq c_{9} \leq \infty$ (51)

其中， $c_{9}$ 为常数。最后，由公式(26)和公式(51)可以得到：

$\lim_{t \to \infty} (x (t) - x_{i} (t) l) = 0, i \in v$ (52)

证明了该多智能体系统的一致性。

3. 仿真与分析

在这个仿真示例中，首先应用一个由5个智能体组成的网络。其中，该一致协议中的耦合参数由公式(10)定义的变步长LMS递归生成。多智能体系统的拓扑结构如图1所示：

公式(10)中的步长 $μ_{i}$ 采用固定步长时，如果步长过大或过小，可能导致多智能体系统收敛速度慢，后期可能不会收敛。因此，在算法的运行初期保持较大的值，随着迭代次数的增加，步长自适应的进行减小。因此，在多次的实验的情况下，将 $μ_{i}$ 的初始数值设置为较大的数值，在之后的迭代过程中设置为可变步长 $μ_{i} = μ_{i} - 0.001 \times n, i \in v$ ，让其随着迭代次数的增加而减小。

表1显示了每个智能体的初始位置和初始的速度。

对图1所示的拓扑结构进行仿真，仿真结果如图2和图3所示。

由于图1所示的拓扑结构含有有向生成树，多智能体的状态变量最后达到了一致。图2显示了每个智能体状态 $x_{i} (t), i \in v$ 的收敛。图3显示了每个智能体的方向和位置信息。

如果改变该多智能体系统的拓扑结构，使得该图不含有生成树。如图4所示。

对图4所示的拓扑结构进行仿真。仿真结果如图5和图6所示。

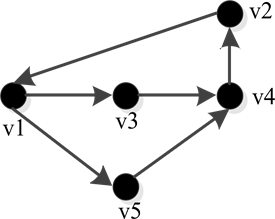
Figure 1. A topology with a span ning tree

图1. 含有生成树的拓扑结构

Table 1. The initial positions and velocities of the agents

表1. 智能体的初始位置和初始速度

Figure 2. The amplitude of velocities

图2. 智能体速度的幅值

Figure 3. Positions and directions of agents at different iterations

图3. 智能体的位置和方向

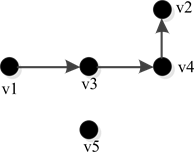
Figure 4. A topology without a span ning tree

图4. 不含生成树的拓扑结构

Figure 5. The amplitude of velocities

图5. 智能体速度的幅值

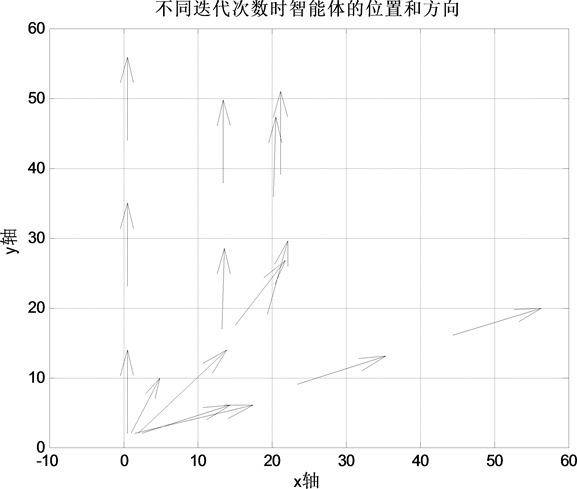
Figure 6. Positions and directions of agents at different iterations

图6. 智能体的位置和方向

由仿真结果可以看到，由于图4所示的拓扑结构不含有向生成树，所以得到的多智能体系统的状态变量没有实现一致性。也可以由图4所示的拓扑结构图进行直观的分析，由于智能体5不接收任何智能体的信息，所以，智能体5的状态一直保持不变。智能体2也不接收其他智能体的任何信息，所以智能体1、3、4的状态值最后收敛到智能体2的状态值。

4. 结论

本文针对多智能体系统的一致性问题进行了研究，提出了一种基于LMS的变步长自调优一致性算法，证明了该算法收敛。最后通过在不同拓扑结构中仿真，验证了所设计一致性算法的正确性。

文章引用

韩宗亭,吴宪祥,呼香艳,郭宝龙,陈曦. 基于LMS的多智能体系统变步长自调优一致性
Variable Step Self-Tuning Consensus of Multi-Agent Systems with Least Mean Squares Method[J]. 计算机科学与应用, 2018, 08(06): 877-887. https://doi.org/10.12677/CSA.2018.86097

参考文献

1. Olfati-Saber, R. and Murray, R.M. (2004) Consensus Problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Transactions on Automatic Control, 49, 1520-1533. https://doi.org/10.1109/TAC.2004.834113

2. Ren, W. and Beard, R.W. (2005) Consensus Seeking in Mul-ti-Agent Systems under Dynamically Changing Interaction Topologies. IEEE Transactions on Automatic Control, 50, 655-661. https://doi.org/10.1109/TAC.2005.846556

3. 李静, 方正. 分数阶非线性多智能体系统的一致性研究[J]. 计算机工程与应用, 2016, 52(23): 63-67.

4. Li, T. and Zhang. J.F. (2010) Consensus Conditions of Mul-ti-Agent Systems with Time-Varying Topologies and Stochastic Communication Noises. IEEE Transactions on Auto-matic Control, 55, 2043-2057. https://doi.org/10.1109/TAC.2010.2042982

5. Dong, X.W., Xi, J.X., Shi, Z.Y., et al. (2013) Practical Consen-sus for High-Order Linear Time-Invariant Swarm Systems with Interaction Uncertainties, Time-Varying Delays and Ex-ternal Disturbances. International Journal of Systems Science, 44, 1843-1856. https://doi.org/10.1080/00207721.2012.670296

6. Jadbabaie, A., Lin, J. and Morse, A.S. (2003) Coordination of Groups of Mobile Autonomous Agents Using Nearest Neighbor Rules. IEEE Transactions on Automatic Control, 48, 988-1001. https://doi.org/10.1109/TAC.2003.812781

7. 王品, 姚佩阳. 具有不同输入时延的二阶多智能体系统一致性[J]. 复杂系统与复杂性科学, 2016, 13(4): 102-107.

8. Bai, H., Arcak, M. and Wen, J. (2011) Coopera-tive Control Design: A Systematic-Passivity Based Approach. Springer-Verlag, New York. https://doi.org/10.1007/978-1-4614-0014-1

9. Ma, T.D., Zhang, L.Y. and Gu, Z.Y. (2016) Further Studies on Impulsive Consensus of Multi-Agent Nonlinear Systems with Control Gain Error. Neurocomputing, 190, 140-146. https://doi.org/10.1016/j.neucom.2016.01.024

10. 袁玩贵, 屈百达. 受干预多智能体系统的一致性分析及控制[J]. 控制与决策, 2016, 31(1): 187-192.

11. Cao, Y., Yu, W., Ren, W. and Chen, G. (2013) An Overview of Recent Progress in the Study of Distributed Multi-Agent Coordination. IEEE Transactions on Industrial Informatics, 9, 427-438. https://doi.org/10.1109/TII.2012.2219061

12. Zhou, J., Lu, J. and Lü, J. (2006) Adaptive Synchronization of an Uncertain Complex Dynamical Network. IEEE Transactions on Automatic Control, 51, 652-656. https://doi.org/10.1109/TAC.2006.872760

13. Zhou, J., Lu, J. and Lü, J. (2008) Pinning Adaptive Synchroniza-tion of a General Complex Dynamical Network. Automatica, 44, 996-1003. https://doi.org/10.1016/j.automatica.2007.08.016

14. DeLellis, P., diBernardo, M. and Garofalo, F. (2009) Novel Decentralized Adaptive Strategies for Synchronization of Complex Networks. Automatica, 45, 1312-1318. https://doi.org/10.1016/j.automatica.2009.01.001

15. Das, A. and Lewis, F. (2010) Distributed Adaptive Control for Synchronization of Unknown Nonlinear Networked Systems. Automatica, 46, 2014-2021. https://doi.org/10.1016/j.automatica.2010.08.008

16. Yu, H. and Xia, X. (2012) Adaptive Consensus for Mul-ti-Agents in Networks with Jointly Connected Topologies. Automatica, 48, 1783-1790. https://doi.org/10.1016/j.automatica.2012.05.068

17. Li, Z., Ren, W., Liu, X. and Xie, L. (2013) Distributed Con-sensus of Linear Multi-Agent Systems with Adaptive Dynamic Protocols. Automatica, 49, 1986-1995. https://doi.org/10.1016/j.automatica.2013.03.015

18. Radenkovic, M. and Bose, T. (2015) On Multi-Agent Self-Tuning Consensus. Pergamon Press, Inc., Oxford.

19. 张清华. 图论及其应用[M]. 北京: 清华大学出版社, 2013: 2-4.

20. 吴永红, 刘敬贤. 多智能体网络一致性协同控制理论及应用[M]. 北京: 科学出版社, 2013.

21. 李霄剑, 王永, 陈绍青, 等. 一种方向优化最小均方算法[J]. 电子与信息学报, 2014, 36(6): 1348-1354.

期刊菜单