Mechanical Engineering and Technology
Vol.07 No.03(2018), Article ID:25664,6
pages
10.12677/MET.2018.73025
An Approach to Measuring No-Load Rotational Torque of Self-Lubricating Spherical Bearing in Rolling Clearance Process
Hongyu Liu1,2
1Shanghai Bearing Technology Research Institute, Shanghai
2Shanghai Special Bearing Engineering Technology Center, Shanghai
Received: Jun. 1st, 2018; accepted: Jun. 21st, 2018; published: Jun. 28th, 2018

ABSTRACT
Rolling clearance is a type of means of adjusting the no-load rotational breakaway torque of a self-lubricating spherical bearing. Based on the bilinear model of rotational torque vs. rolling force in the rolling process, a method to evaluating the no-load torque is present, by detecting the variations in the rotational torque with the rolling force during the uploading or unloading stage in the process. The method proposed in this paper helps to improve the accuracy of rolling clearance of self-lubricating spherical bearings.
Keywords:Self-Lubricating Spherical Bearing, No-Load Rotational Breakaway Torque, On-Line Measure
自润滑关节轴承游隙调节工序中的无载阻力矩在线测试技术
刘红宇1,2
1上海市轴承技术研究所,上海
2上海特种轴承工程技术中心,上海
收稿日期:2018年6月1日;录用日期:2018年6月21日;发布日期:2018年6月28日

摘 要
滚轧游隙是自润滑关节轴承调节无载启动力矩的一种工艺手段。在建立滚轧中被轧轴承的摩擦力矩关于滚轧力的双线性模型的基础上,提出了通过连续检测滚轧加载过程或卸载过程中被测轴承的摩擦力矩和相应的滚轧力,进行无载启动力矩的在线检测的方法。本文提出的方法有助于提高自润滑关节轴承滚轧游隙的精度。
关键词 :自润滑关节轴承,无载启动力矩,在线检测

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自润滑关节轴承是一种球面滑动轴承,由一个外球面内圈和一个内球面上粘贴了自润滑织物衬垫的外圈构成。自润滑关节轴承的无载启动力矩是指轴承不受载荷时,轴承内外圈从静止状态到开始相对转动的瞬间所需要克服的摩擦阻力矩。它综合反映了轴承内外圈球面的贴合度、预紧状况以及自润滑衬垫的摩擦性能等,是自润滑关节轴承的一项重要的技术参数。近几年来,尽管国内外关于自润滑关节轴承启动力矩的检测标准还比较粗放 [1] ,随着对自润滑关节轴承研究的不断深入,无载启动力矩的检测技术逐步完善 [2] [3] [4] 。
滚轧是目前整体外圈式自润滑关节轴承调节游隙的一种有效工艺,也是调节无载启动力矩的主要手段。在传统的滚游隙工艺中,滚轧力、滚轧次数、滚轧速度等工艺参数的设置主要依赖于操作人员的经验。由于整体外圈式轴承在挤压成形后内外圈的预紧量大小不一,所以这种滚游隙工艺无法保证产品无载启动力矩的批产一致性和均匀性。滚游隙过程实际上是轴承无载启动力矩由大到小的调节过程,无载启动力矩的大小反映了滚轧游隙的进度。本文作者研发了通过在线检测的被轧轴承的摩擦阻力矩来反馈控制滚轧过程的工艺技术 [5] ,产品无载启动力矩的批产一致性虽然有了显著的提高,但由于无载启动力矩在线检测困难,尚不能完全达到要求。本文研究在滚轧工艺中自润滑关节轴承无载启动力矩的在线测试方法。
2. 自润滑关节轴承游隙调节工序中的无载阻力矩在线检测原理
图1所示的是一种三辊式滚轧自润滑关节轴承游隙工艺。在一定的滚轧力作用下,三根轧辊从外辗压轴承外圈,松弛被轧轴承。在线检测轴承的阻力矩,就是被测轴承在这种特殊的安装状态下,检测轴承内外圈之间的阻力矩。图2是轴承阻力矩的一种测量方案。在此方案中,轧辊起到夹持外圈并驱动外圈相对内圈旋转的作用,轴承内圈通过一台扭矩传感器和机架固定。注意到,轧辊的夹持力改变了被轧轴承的“无载”状态,使启动力矩变大。显然,夹持力越小,对启动力矩的影响越小,夹持被轧轴承的能力也越小,越容易出现打滑现象。在保持轧辊和轴承外圈作纯滚动的前提下,如何清除夹持的影响是在线检测无载启动力矩的关键。
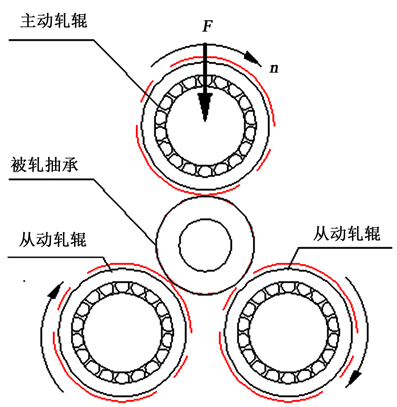
Figure 1. The clearance process of three-roll-type rolling self-lubricating spherical bearing
图1. 三辊式滚轧自润滑关节轴承游隙工艺
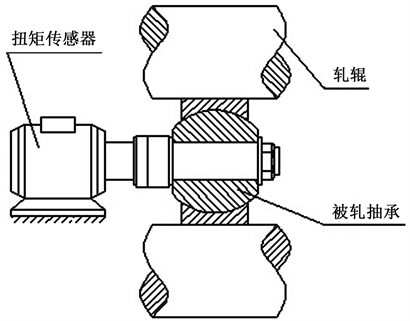
Figure 2. The measurement scheme of bearing resistance moment
图2. 轴承阻力矩的测量方案
2.1. 三辊夹持下的阻力矩模型
形成自润滑关节轴承的无载启动力矩的部分原因是轴承内外圈配合具有一定的过盈量。假设:1) 内外圈为刚体,衬垫为线性弹性体;2) 无载时,内外圈之间的衬垫压缩量(即过盈量)在圆周方向均匀分布;3) 轴承摩擦副间的摩擦力满足库仑定律。当轴承受径向载荷作用,产生的径向轴承位移小于过盈量时,外圈、衬垫及内圈在整个圆周内仍保持过盈状态;当径向轴承位移大于过盈量时,内外圈局部出现间隙。理论分析表明 [6] ,在内外圈始终保持过盈配合状态的条件下,径向载荷对轴承的启动力矩无影响。当轴承出现局部间隙后,启动力矩随着径向载荷的增加而线性增加。
在三辊夹持下的轴承承受三个方向的径向力,产生阻力矩的机理和单个径向力的作用类似。设被轧轴承的无载启动力矩为Ts0,外圈夹持力为Ffix,在线测量时被轧轴承的阻力矩可以简化为以下的双线性模型:
(1)
其中 为夹持力影响系数,和被测轴承结构及轧辊有关;Ffix0为使被轧轴承出现出现间隙的最小滚轧力,和被测轴承的结构和过盈量有关。
注意到,扭矩传感器测得的扭矩不一定就是被测轴承的阻力矩。当外圈和轧辊打滑时,反映的是外圈和轧辊的摩擦力矩。设轧辊和轴承外圈之间的摩擦系数为 ,被测轴承外圈半径为R,外圈不打滑的条件
(2)
其中 称为轴承外圈和轧辊的摩擦半径。这个摩擦半径可以在滚轧初期(被轧轴承的启动力矩较大时)或滚轧力较小时测的。
2.2. 三辊夹持下无载启动力矩的检测
被轧轴承阻力矩的检测可安排在一次滚轧开始前的加载过程或滚轧结束后的卸载过程中进行。在这过程中,连续检测的阻力矩和相应的滚轧力,得到一组原始数据对(Tsi,Ffixi) ( )。根据这些原始数据对,通过以下两个步骤的数据分析评估无滚轧力下的启动力矩,即无载启动力矩。
1) 轴承外圈和轧辊的摩擦半径的评估
根据式(2),轴承外圈和轧辊的摩擦半径即为在打滑条件下的阻力矩和夹紧力之比,可按以下数据处理方法提取:
a) 根据轧辊和轴承外圈材料,初定轴承外圈摩擦半径 ,从原始数据中选取满足 的K对数据对(Tsj,Ffixj) ( )。
b) 计算阻力矩和夹紧力之比的均值和均方差
(3)
(4)
c) 若误差 超过允差,剔除其中的超差的数据对,转(b);否则,得到轴承外圈摩擦半径 。
2) 无载启动力矩的评估
从原始数据中选取满足 的M对数据(Tsj,Ffixj) ( ),按式(1)进行两直线段的折线拟合,求得无载启动力矩。
关于多直线段的线性拟合,文献 [7] 等给出了各种通用算法。但是,鉴于本问题的特殊性,可以采用如下更为简便的算法。
a) 按Ffix降序排列数据对(Tsj,Ffixj) ( )。
b) 取 ,对(Tsi,Ffixi) ( )利用最小二乘法拟合成直线 ;
c) 将(Tsi,Ffixi) ( )拟合成水平线,即
(5)
d) 取双线段拟合误差
(6)
搜索p,使E最小。
3. 试验分析和讨论
取一批已知启动力矩值的自润滑关节轴承成品为试验轴承,在2T滚轧机上进行模拟滚游隙过程中的无载启动力矩在线检测试验。试验轴承的型号为GE15,试验前在计量室用专用的关节轴承无载启动力矩仪检测启动力矩。在线检测选择在滚轧卸载过程中进行,将夹持力从500 N开始以20 N/s的速率递减至0 N,连续同步记录卸载过程的夹持力和阻力矩数据。将这些数据按本文给出的方法处理成无载启动力矩,结果如表1所示。
图3是3#试件(无载启动力矩为0.110~0.121 Nm)在线检测时的夹持力-时间、阻力矩-时间曲线,相应的阻力矩-夹持力曲线如图4所示。从图4中可以看出,阻力矩-夹持力曲线基本呈现三段直线的形态:夹持力大于100 N的阶段为一段直线;夹持力在70 N附近,曲线逐渐转平,阻力矩接近无载力矩;小于50 N时,阻力矩值快速直线下降,此时轴承外圈与轧辊开始打滑,根据阻力矩和夹持力曲线斜率,可以求得外圈的摩擦半径约为0.039 m。对夹持力大于50 N的曲线部分进行双直线,得到双直线方程为:
由此可得,轴承的无载启动力矩为 ,略高于离线测得的无载力矩值。
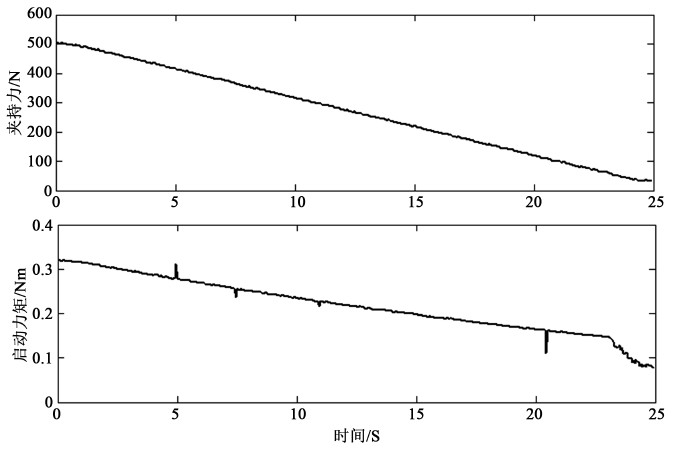
Figure 3. The grasping force and resistant moment curves with respect to time respectively during the process of roll unloading
图3. 滚轧卸载过程中夹持力和阻力矩曲线分别关于时间的曲线
Table 1. The off-line and on-line measured result comparison of starting torque for GE15
表1. GE15启动力矩离线和在线测量结果比较

Figure 4. The curve of grasping force with respect to resistant moment
图4. 阻力矩关于夹持力的曲线
无载启动力矩的在线检测精度主要受限于被测轴承的夹持方式和滚轧机滚轧力的测量精度。由于滚轧力(夹持力)的存在,无法在滚轧过程中直接检测到被轧轴承的无载启动力矩,而只能通过类似于外插法的方法进行估算,所以产生较大的误差纯属正常。从表1可以看出,1) 除了启动力矩极小的轴承外,在线检测的相对误差为10%~30%,基本可以满足滚游隙的控制要求。2) 检测误差一般随启动力矩的减小而增大。相对于滚游隙所需的滚轧力,检测用的夹持力要小的多。夹持力越小,其控制和测量误差越大,这是造成上述现象的主要原因。3) 在线检测结果一般大于离线检测结果。这是由于在实际检测中得不到足够长的双线性模型中的水平线。提高轧辊和外圈的摩擦系数,有助于降低轧辊和轴承外圈不打滑的最小夹持力,扩大阻力矩的检测范围,可以提高无载力矩的检测精度。
4. 结论
利用自润滑关节轴承滚轧游隙过程中的加载或卸载过程,通过连续检测被轧轴承的阻力矩和滚轧力,可以间接检测被轧轴承的无载启动力矩。在线检测到的无载启动力矩反映了滚轧游隙过程中轴承间隙的调节程度,有助于精密控制轴承游隙的滚轧工艺。
文章引用
刘红宇. 自润滑关节轴承游隙调节工序中的无载阻力矩在线测试技术
An Approach to Measuring No-Load Rotational Torque of Self-Lubricating Spherical Bearing in Rolling Clearance Pro-cess[J]. 机械工程与技术, 2018, 07(03): 200-205. https://doi.org/10.12677/MET.2018.73025
参考文献
- 1. 张令, 赵颖春. 自润滑关节轴承无载旋转启动力矩测量标准分析[J]. 润滑与密封, 2015, 40(2): 112-115.
- 2. 林晶, 张令. 湿热对自润滑关节轴承无载旋转启动力矩的影响[J]. 轴承, 2013(8): 30-32.
- 3. 李宝福, 刘亮. 自润滑关节轴承无载启动力矩测量方法分析[J]. 轴承, 2013(1): 81-83.
- 4. 从志斌, 李宝福. 自润滑关节轴承摆动摩擦力矩的测量方法[J].计量与测试技术, 2016, 43(9): 43-46.
- 5. 刘红宇, 李宝福. 自润滑关节轴承力矩在线即时检测与控制系统及方法[P]. 中国专利: 201110456320.4, 2012-07-04.
- 6. 李英, 李宝福, 等. 自润滑关节轴承接触应力分析[J]. 轴承, 2016(5): 32-36.
- 7. 田垅, 刘宗田. 最小二乘法分段直线拟合[J]. 计算机科学, 2012, 39(6A): 482-484.
